1. shopping
2. auctions

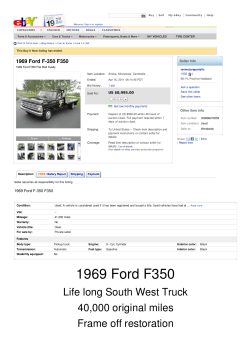
Asymmetric Information, Adverse Selection and
Seller Revelation on eBay Motors∗
Gregory Lewis†
Department of Economics
University of Michigan
December 28, 2006
Abstract
Since the pioneering work of Akerlof (1970), economists have been aware of the adverse
selection problem that asymmetric information can create in durable goods markets. The
success of eBay Motors, an online auction market for used cars, thus poses something of a
puzzle. I argue that the key to resolving this puzzle is the auction webpage, which allows
sellers to reduce information asymmetries by revealing credible signals about car quality
in the form of text, photos and graphics. To validate my claim, I develop a new model of
a common value eBay auction with costly seller revelation and test its implications using
a unique panel dataset of car auctions from eBay Motors. Precise testing requires a structural estimation approach, so I develop a new pseudo-maximum likelihood estimator for
this model, accounting for the endogeneity of information with a semiparametric control
function. I find that bidders adjust their valuations in response to seller revelations, as the
theory predicts. To quantify how important these revelations are in reducing information
asymmetries, I simulate a counterfactual in which sellers cannot post information to the
auction webpage and show that in this case a significant gap between vehicle value and
expected price can arise. Since this gap is dramatically narrowed by seller revelations, I conclude that information asymmetry and adverse selection on eBay Motors are endogenously
reduced by information transmitted through the auction webpage.
∗
I would like to thank the members of my thesis committee, Jim Levinsohn, Scott Page, Lones Smith and
especially Pat Bajari for their helpful comments. I have also benefited from discussions with Jim Adams,
Tilman B¨
orgers, Han Hong, Kai-Uwe K¨
uhn, Serena Ng, Nicola Persico, Dan Silverman, Jagadeesh Sivadasan,
Doug Smith, Charles Taragin and seminar participants at the Universities of Michigan and Minnesota. All
remaining errors are my own.
†
Email: [email protected]
1
Introduction
eBay Motors is, at first glance, an improbable success story. Ever since Akerlof’s classic paper,
the adverse selection problems created by asymmetric information have been linked with their
canonical example, the used car market. One might think that an online used car market,
where buyers usually don’t see the car in person until after purchase, couldn’t really exist.
And yet it does - and it prospers. eBay Motors is the largest used car market in America,
selling over 15000 cars in a typical month. This poses a question: How does this market limit
asymmetric information problems?
The answer, this paper argues, is that the seller may credibly reveal his private information
through the auction webpage. Consider Figure 1, which shows screenshots from an eBay
Motors auction for a Corvette Lingenfelter. The seller has provided a detailed text description
of the features of the car and taken many photos of both the interior and the exterior. He has
in addition taken photographs of original documentation relating to the car, including a series
of invoices for vehicle modifications and an independent analysis of the car’s performance. This
level of detail appears exceptional, but it is in fact typical in most eBay car auctions for sellers
to post many photos, a full text description of the car’s history and features, and sometimes
graphics showing the car’s condition.
I find strong empirical evidence that buyers respond to these seller revelations. The data
is consistent with a model of costly revelation, in which sellers weigh costs and benefits in
deciding how much detail about the car to provide. An important prediction of this model is
that bidders’ prior valuations should be increasing in the quantity of information posted on the
webpage. I find that this is the case. Using the estimated structural parameters, I simulate a
counterfactual in which sellers cannot reveal their private information on the auction webpage.
In that case a significant gap arises between the value of the vehicle and the expected price.
I quantify this price-value gap, showing that seller revelations dramatically narrow it. Since
adverse selection occurs when sellers with high quality cars are unable to receive a fair price
for their vehicle, I conclude that these revelations substantially limit asymmetric information
and thus the potential for adverse selection.
My empirical analysis of this market proceeds through the following stages. Initially, I run
a series of hedonic regressions to demonstrate that there is a large, significant and positive
relationship between auction prices and the number of photos and bytes of text on the auction
webpage. To explain this finding, I propose a stylized model of a common values auction
on eBay with costly revelation by sellers, and subsequently prove that in equilibrium, there
is a positive relationship between the number of signals revealed by the seller and the prior
1
Figure 1: Information on an auction webpage On this auction webpage, the seller has provided
many different forms of information about the Corvette he is selling. These include the standardized
eBay description (top panel), his own full description of the car’s options (middle panel), and many
photos (two examples are given in the bottom panel). The right photo is of the results of a car
performance analysis done on this vehicle.
2
valuation held by bidders. In the third stage, I test this prediction. A precise test requires
that I structurally estimate my eBay auction model, and I develop a new pseudo-maximum
likelihood estimation approach to do so. I consider the possibility that my information measure
is endogenous, providing an instrument and a semiparametric control function solution for
endogeneity. The final step is to use the estimated parameters of the structural model to
simulate a counterfactual and quantify the impact of public seller revelations in reducing the
potential for adverse selection.
The first of these stages requires compiling a large data set of eBay Motors listings for a 6 month
period, containing variables relating to item, seller and auction characteristics. I consider two
measures of the quantity of information on an auction webpage: the number of photographs,
and the number of bytes of text. Through running a series of hedonic regressions, I show that
these measures are significantly and positively correlated with price. The estimated coefficients
are extremely large, and this result proves robust to controls for marketing effects, seller size
and seller feedback. This suggests that it is the webpage content itself rather than an outside
factor that affects prices, and that the text and photos are therefore genuinely informative. It
leaves open the question of why the quantity of information is positively correlated with price.
I hypothesize that this is an artifact of selection, where sellers with good cars put up more
photos and text than those selling lemons.
To formally model this, in the second stage I propose a stylized model of an eBay auction.
Bidders are assumed to have a common value for the car, since the common values framework
allows for bidder uncertainty, and such uncertainty is natural in the presence of asymmetric
information.1 Sellers have access to their own private information, captured in a vector of
private signals, and may choose which of these to reveal. The seller’s optimal strategy is
characterized by a vector of cutoff values, so that a signal is revealed if and only if it is
sufficiently favorable. In equilibrium, the model predicts that bidders’ prior valuation for the
car being sold is increasing in the number of signals revealed by the seller.
I test this prediction in the third stage by structurally estimating the common value auction
model. It is necessary to proceed structurally because the prediction is in terms of a latent
variable - the bidder’s prior value - and is thus only directly testable in a structural model.
Strategic considerations arising from the Winner’s Curse preclude an indirect test based on the
relationship between price and information measures. In estimating the model, I propose a new
pseudo-maximum likelihood estimation approach that addresses two of the common practical
concerns associated with such estimation. One of the concerns is that in an eBay context it is
1
I also show that this assumption finds support in the data. In an extension, to be found in the appendix, I
test the symmetric common values framework used here against a symmetric private values alternative. I reject
the private values framework at the 5% level.
3
difficult to determine which bids actually reflect the bidder’s underlying valuations, and which
bids are spurious. Using arguments similar to those made by Song (2004) for the independent
private values (IPV) case, I show that in equilibrium the final auction price is in fact equal
to the valuation of the bidder with second most favorable private information. I obtain a
robust estimator by maximizing a function based on the observed distribution of prices, rather
than the full set of observed bids. The second concern relates to the computational cost of
computing the moments implied by the structural model, and then maximizing the resulting
objective function. I show that by choosing a pseudo-maximum likelihood approach, rather
than the Bayesian techniques of Bajari and Horta¸csu (2003) or the quantile regression approach
of Haile, Hong, and Shum (2003), one is able to use a nested loop procedure to maximize
the objective function that limits the curse of dimensionality. This approach also provides
transparent conditions for the identification of the model.
The theory predicts that bidders respond to the information content of the auction webpage,
but this is unobserved by the econometrician. Moreover, under the theory, this omitted content
is certainly correlated with quantitative measures of information such as the number of photos
and number of bytes of text. To address this selection problem I adopt a semiparametric
control function approach, forming a proxy for the unobserved webpage content using residuals
from a nonparametric regression of the quantity of information on exogenous variables and an
instrument. I exploit the panel data to obtain an instrument, using the quantity of information
provided for the previous car sold by that seller. As the theory predicts, I find that the quantity
of information is endogenous and positively correlated with the prior mean valuation of bidders.
My results suggest that the information revealed on the auction webpage reduces the information asymmetry between the sellers and the bidders. One would thus expect that seller
revelations limit the potential for adverse selection. My final step is to investigate this conjecture with the aid of a counterfactual simulation. I simulate the bidding functions and compute
expected prices for the observed regime and a counterfactual in which sellers cannot reveal
their private information through the auction webpage. In the counterfactual regime, sellers
with a “peach” - a high quality car - cannot demonstrate this to bidders except through private
communications. The impact of removing this channel for information revelation is significant,
driving a wedge between the value of the car and the expected price paid by buyers. I find
that a car worth 10% more than the average car with its characteristics will sell for only 6%
more in the absence of seller revelation. This gap disappears when sellers can demonstrate the
quality of their vehicle by posting text, photos and graphics to the auction webpage.
I make a number of contributions to the existing literature. Akerlof (1970) showed that in a
market with information asymmetries and no means of credible revelation, adverse selection
4
can occur. Grossman (1981) and Milgrom (1981) argued that adverse selection can be avoided
when the seller can make ex-post verifiable and costless statements about the product he is
selling. I consider the intermediate case where the seller must pay a cost for credibly revealing
his private information and provide structural analysis of a market where this is the case.
Estimation and simulation allow me to quantify by how much credible seller revelation reduces
information asymmetries and thus the potential for adverse selection. The contributes to the
sparse empirical literature on adverse selection which has until now focused mainly on insurance
markets (Cohen and Einav (2006), Chiappori and Salanie (2000)).
In the auctions literature Milgrom and Weber (1982) show that in a common value auction
sellers should commit a priori to revealing their private information about product quality if
they can do so. But since private sellers typically sell a single car on eBay Motors, there is no
reasonable commitment device and it is better to model sellers as first observing their signals
and then deciding whether or not to reveal. This sort of game is tackled in the literature on
strategic information revelation. The predictions of such models depend on whether revelation
is costless or not: in games with costless revelation, Milgrom and Roberts (1986) have shown
that an unravelling result obtains whereby sellers reveal all their private information. By
contrast, Jovanovic (1982) shows that with revelation costs it is only the sellers with sufficiently
favorable private information that will reveal. Shin (1994) obtains a similar partial revelation
result in a setting without revelation costs by introducing buyer uncertainty about the quality
of the seller’s information. My model applies these insights in an auction setting, showing
that with revelation costs, equilibrium is characterized by partial revelation by sellers. I also
extend to the case of multidimensional private information, showing that the number of signals
revealed by sellers is on average positively related to the value of the object. This relates the
quantity of information to its content.
The literature on eBay has tended to focus on the seller reputation mechanism. Various authors
have found that prices respond to feedback ratings, and have suggested that this is due to the
effect of these ratings in reducing uncertainty about seller type (Resnick and Zeckhauser (2002),
Melnik and Alm (2002), Houser and Wooders (2006)). I find that on eBay Motors the size
of the relationship between price and information measures that track webpage content is far
larger than that between price and feedback ratings. This suggests that in analyzing eBay
markets with large information asymmetries, it may also be important to consider the role
of webpage content in reducing product uncertainty. I contribute to the literature here by
providing simple information measures, and showing that they explain a surprisingly large
amount of the underlying price variation in this market.
Finally, I make a number of methodological contributions with regard to auction estimation.
5
Bajari and Horta¸csu (2003) provide a clear treatment of eBay auctions, providing a model which
can explain late bidding and a Bayesian estimation strategy for the common values case. Yet
their model implies that an eBay auction is strategically equivalent to a second price sealed bid
auction, and that all bids may be interpreted as values. I incorporate the insights of Song (2004)
in paying more careful attention to bid timing and proxy bidding, and show that only the final
price in an auction can be cleanly linked to the distribution of bidder valuations. I provide
a pseudo maximum likelihood estimation strategy that uses only the final price from each
auction, and is therefore considerably more robust. There are also computational advantages
to my common values estimation approach relative to that of Bajari and Horta¸csu (2003) and
the quantile regression approach of Hong and Shum (2002). One important potential problem
with all these estimators lies in not allowing for unobserved heterogeneity and endogeneity. For
the independent private values case, Krasnokutskaya (2002) and Athey, Levin, and Seira (2004)
have provided approaches for dealing with unobserved heterogeneity. Here I develop conditions
under which a semiparametric control function may be used to deal with endogeneity provided
an appropriate instrument can be found. In sum, I provide a robust and computable estimator
for common value eBay auctions. I also provide an implementation of the test for common
values suggested by Athey and Haile (2002) in the appendix, using the subsampling approach
of Haile, Hong, and Shum (2003).
This research leads me to three primary conclusions. First, webpage content in online auctions
informs bidders and is an important determinant of price. Bidder behavior is consistent with a
model of endogenous seller revelation, where sellers only reveal information if it is sufficiently
favorable, and thus bidders bid less on objects with uninformative webpages. Second, quantitative measures of information serve as good proxies for content observed by buyers, but not the
econometrician. This follows from the theory which yields a formal link between the number
of signals revealed by sellers and the content of those signals. Finally, and most important,
the auction webpage allows sellers to credibly reveal the quality of their vehicles. Although
revelation costs prevent full revelation, information asymmetries are substantively limited by
this institutional feature and the gap between values and prices is considerably smaller than it
would be if such revelations were not possible. I conclude that seller revelations through the
auction webpage reduce the potential for adverse selection in this market.
The paper proceeds as follows. Section 2 outlines the market, and section 3 presents the reduced form empirical analysis. Section 4 introduces the auction model with costly information
revelation, while section 5 describes the estimation approach. The estimation results follow in
section 6. Section 7 details the counterfactual simulation and section 8 concludes.2
2
Proofs of all propositions, as well as most estimation results, are to be found in the appendix.
6
2
eBay Motors
eBay Motors is the automobile arm of online auctions giant eBay. It is the largest automotive
site on the Internet, with over $1 billion in revenues in 2005 alone. Every month, approximately
95000 passenger vehicles are listed on eBay, and about 15% of these will be sold on their first
listing.3 This trading volume dwarfs those of its online competitors, the classified services
cars.com, autobytel.com and Autotrader.com. In contrast to these sites, most of the sellers
on eBay Motors are private individuals, although dealers still account for around 30% of the
listings.
Listing a car on eBay Motors is straightforward. For a fixed fee of $40, a seller may post a
webpage with photos, a standardized description of the car, and a more detailed description
that can include text and graphics. The direct costs of posting photos, graphics and text
are negligible: text and graphics are free, while each additional photo costs $0.15. But the
opportunity costs are considerably higher, as it is time-consuming to take, select and upload
photos, write the description, generate graphics, and fill in the forms required to post all of
these to the auction webpage.4
Figure 2 shows part of the listing by a private seller who used eBay’s standard listing template.
In addition to the standardized information provided in the table at the top of the listing, which
includes model, year, mileage, color and other features, the seller may also provide his own
detailed description. In this case the seller has done poorly, providing just over three lines of
text. He also provided just three photos. This car, a 1998 Ford Mustang with 81000 miles on
the odometer, received only four bids, with the highest bid being $1225.
Figure 3 shows another 1998 Ford Mustang, in this case with only 51000 miles. The seller is a
professional car dealership, and has used proprietary software to create a customized auction
webpage. This seller has provided a number of pieces of useful information for buyers: a text
based description of the history of the car, a full itemization of the car features in a table, a
free vehicle history report through CARFAX, and a description of the seller’s dealership. This
listing also included 28 photos of the vehicle. The car was sold for $6875 after 37 bids were
placed on it.
The difference between these outcomes is striking. The car listed with a detailed and informative webpage sold for $1775 more than the Kelley Blue Book private party value, while that
with a poor webpage sold for $3475 less than the corresponding Kelley Blue Book value. This
3
The remainder are either re-listed (35%), sold elsewhere or not traded. For the car models in my data, sales
are more prevalent, with about 30% sold on their first listing.
4
Professional car dealers will typically use advanced listing management software to limit these costs. Such
software is offered by CARad (a subsidiary of eBay), eBizAutos and Auction123.
7
Figure 2: Example of a poor auction webpage This webpage consists mainly of the standardized information required for a listing on eBay. The seller has provided little additional information
about either the car or himself. Only three photos of the car were provided. In the auction, the seller
received only four bids, with the highest bid being $1225. The Kelley Blue Book private party value,
for comparison, is $4700.
Figure 3: Example of a good auction webpage The dealer selling this vehicle has used
proprietary software to create a professional and detailed listing. The item description seen on the
right, contains information on the car, a list of all the options included, warranty information, and a
free CARFAX report on the vehicle history. The dealer also posted 28 photos of the car. This car
received 37 bids, and was sold for $6875. The Kelley Blue Book retail price, for comparison, is $7100,
while the private party value is $5100.
8
Figure 4: Additional information The left panel shows a graphic that details the exterior condition of the vehicle. The right panel shows the Kelley Blue Book information for the model-year of
vehicle being auctioned.
suggests that differences in the quality of the webpage can be important for auction prices.
How can webpages differ? Important sources of differences include the content of the textbased description, the number of photos provided, the information displayed in graphics, and
information from outside companies such as CARFAX. Examples of the the latter two follow
in Figure 4. In the left panel I show a graphic showing the condition of the exterior of the
car. In the right panel, I show the Kelley Blue Book information posted by a seller in order to
inform buyers about the retail value of the vehicle.
It is clear that many of these pieces of information, such as photos and information from outside
institutions, are hard to fake. Moreover, potential buyers have a number of opportunities to
verify this information. Potential buyers may also choose to acquire vehicle history reports
through CARFAX or Autocheck.com, or purchase a third party vehicle inspection from an
online service for about $100. Bidders may query the seller on particular details through
direct communication via e-mail or telephone. Finally, blatant misrepresentation by sellers
is subject to prosecution as fraud. In view of these institutional details, I will treat seller
revelations as credible throughout this paper. All of these sources of information - the text,
photos, graphics and information from outside institutions, as well as any private information
acquired - act to limit the asymmetric information problem faced by bidders. The question
I wish to examine is how important these sources of information are for auction prices. This
question can only be answered empirically, and so it is to the data that I now turn.
9
3
Empirical Regularities
3.1
Data and Variables
I collected data from eBay Motors auctions over a six month period.5 I drop observations with
nonstandard or missing data, re-listings of cars, and those auctions which received less than
two bids.6 I also drop auctions in which the webpage was created using proprietary software.7
The resulting dataset consists of over 18000 observations of 18 models of vehicle. The models of
vehicle may be grouped into three main types: those which are high volume Japanese cars (e.g.
Honda Accord, Toyota Corolla), a group of vintage and newer “muscle” cars (e.g. Corvette,
Mustang), and most major models of pickup truck (e.g. Ford F-series, Dodge Ram).
The data contain a number of item characteristics including model, year, mileage, transmission
and title information. I also observe whether the vehicle had an existing warranty, and whether
the seller has certified the car as inspected.8 In addition, I have data on the seller’s eBay
feedback and whether they provided a phone number and address in their listing. I can also
observe whether the seller has paid an additional amount to have the car listing “featured”,
which means that it will be given priority in searches and highlighted.
Two of the most important types of information that can be provided about the vehicle by the
seller are the vehicle description and the photos. I consider two simple quantitative measures
of these forms of information content. The first measure is the number of bytes of text in the
vehicle description provided by the seller. The second measure is the number of photos posted
on the webpage. I use both of these variables in the hedonic regressions in the section below.
5
I downloaded the auction webpages for the car models of interest every twenty days, recovered the urls for
the bid history, and downloaded the history. I implemented a pattern matching algorithm in Python to parse
the html code and obtain the auction variables.
6
I do this because in order to estimate my structural auction model, I need at least two bids per auction.
Examining the data, I find that those auctions with less than two bids are characterized by extremely high
starting bids (effectively reserves), but are otherwise similar to the rest of the data. One respect in which
there is a significant difference is that in these auctions the seller has provided less text and photos. This is in
accordance with the logic detailed in the rest of the paper.
7
Webpages created using proprietary software are often based on standardized templates, and some of the
text of the item description is not specific to the item being listed. Since one of my information measures is the
number of bytes of text, comparisons of standard eBay listings with those generated by advanced software are
not meaningful.
8
This certification indicates that the seller has either hired an outside company to perform a car inspection.
The results of the inspection can be requested by potential buyers.
10
3.2
Relating Prices and Information
In order to determine the relationship between the amount of text and photos and the final
auction price, I run a number of hedonic regressions. Each specification has the standard form:
log(pj ) = zj β + ε
(1)
where zj is a vector of covariates.9 I estimate the relationship via ordinary least squares (OLS),
including model and title fixed effects.10 I report the results in Table 1, suppressing the fixed
effects.
In the first specification, the vector of covariates includes standard variables, such as age,
mileage and transmission, as well as the log number of bytes of text and the number of photos.
The coefficients generally have the expected sign and all are highly significant.11 Of particular
interest is the sheer magnitude of the coefficients on the amount of text and photos. I find
that postings with twice the amount of text sell for 8.7% more, which for the average car in
the dataset is over $800 more. Likewise, each additional photo on the webpage is associated
with a selling price that is 2.6% higher - a huge effect.
I am not asserting a causal relationship between the amount of text and photos and the auction
price. My claim is that buyers are using the content of the text and photos to make an informed
decision as to the car’s value. The content of this information includes the car’s options, the
condition of the exterior of the vehicle, and vehicle history and usage, all of which are strong
determinants of car value. Moreover, as I will show in the structural model below, buyers will
in equilibrium interpret the absence of information as a bad signal about vehicle quality, and
adjust their bids downwards accordingly. I will also show that the amount of information is an
effective proxy for the content of that information. Thus my interpretation of this regression
is that the large coefficients on text and photos arise because these measures are proxying for
attributes of the vehicle that are unobserved by the econometrician.
In the next four regressions, I explore alternate explanations. The first alternative is that this
is simply a marketing effect, whereby slick webpages with a lot of text and photos attract
more bidders and thus the cars sell for higher prices. I therefore control for the number of
bidders, and also add a dummy for whether the car was a featured listing. I find that adding
these controls does reduce the information coefficients, but they still remain very large. A
9
I use the log of price instead of price as the dependent variable so that it has range over the entire real line.
The seller may report the title of the car as clean, salvage, other or unspecified. The buyer may check this
information through CARFAX.
11
One might have expected manual transmission to enter with a negative coefficient, but I have a large number
of convertible cars and pickups in my dataset, and for these, a manual transmission may be preferable.
10
11
Table 1: Hedonic Regressions
Age
Age Squared
Log of Miles
Log of Text Size (in bytes)
Number of Photos
Manual Transmission
(1)
-0.1961
(0.0019)
0.0039
(0.0000)
-0.1209
(0.0041)
0.0852
(0.0073)
0.0269
(0.0009)
0.0349
(0.0124)
(2)
-0.1935
(0.0018)
0.0038
(0.0000)
-0.1225
(0.0040)
0.0686
(0.0072)
0.0240
(0.0009)
0.0348
(0.0122)
0.2147
(0.0211)
0.0355
(0.0015)
(3)
-0.1931
(0.0018)
0.0038
(0.0000)
-0.1221
(0.0040)
0.0816
(0.0075)
0.0241
(0.0009)
0.0328
(0.0122)
0.2112
(0.0210)
0.0356
(0.0015)
-0.0211
(0.0033)
-0.0031
(0.0015)
(4)
-0.1924
(0.0018)
0.0038
(0.0000)
-0.1215
(0.0040)
0.0794
(0.0076)
0.0234
(0.0009)
0.0338
(0.0122)
0.2113
(0.0211)
0.0355
(0.0015)
-0.0200
(0.0033)
-0.0031
(0.0015)
-0.0020
(0.0015)
0.1151
(0.0123)
-0.0498
(0.0183)
9.7097
(0.0995)
9.5918
(0.0980)
9.5746
(0.0980)
9.5704
(0.0980)
Featured Listing
Number of Bidders
Log Feedback
Percentage Negative Feedback
Total Number of Listings
Phone Number Provided
Address Provided
Warranty
Warranty*Logtext
Warranty*Photos
Inspection
Inspection*Logtext
Inspection*Photos
Constant
(5)
-0.1875
(0.0020)
0.0037
(0.0000)
-0.1170
(0.0041)
0.0978
(0.0085)
0.0260
(0.0010)
0.0319
(0.0121)
0.2125
(0.0210)
0.0357
(0.0015)
-0.0179
(0.0033)
-0.0032
(0.0015)
-0.0019
(0.0015)
0.1193
(0.0122)
-0.0510
(0.0182)
0.8258
(0.1638)
-0.0738
(0.0248)
-0.0189
(0.0031)
0.6343
(0.1166)
-0.0654
(0.0176)
-0.0054
(0.0022)
9.2723
(0.1025)
Estimated standard errors are given in parentheses. The model fits well, with the R2 ranging from 0.58 in (1)
to 0.61 in (5). The nested specifications (2)-(4) include controls for marketing effects, seller feedback and dealer
status. Specification (5) includes warranty and inspection dummies and their interactions with the information
measures.
12
second explanation is that the amount of text and photos are somehow correlated with seller
feedback ratings, which are often significant determinants of prices on eBay. I find not only
that including these controls has little effect on the information coefficients, but that for this
specific market the effects of seller reputation are extremely weak. The percentage negative
feedback has a very small negative effect on price, while the coefficient on total log feedback
is negative, which is the opposite of what one would expect. A possible reason for these
results is that for the used car market, the volume of transactions for any particular seller is
small and this makes seller feedback a weak measure of seller reputation. Another problem is
that feedback is acquired through all forms of transaction, and potential buyers may only be
interested on feedback resulting from car auctions.
Returning to the question of alternative explanations, a third possibility is that frequent sellers
such as car dealerships tend to produce better webpages, since they have stronger incentives to
develop a good template than less active sellers. Then if buyers prefer to buy from professional
car dealers, I may be picking up this preference rather than the effects of information content.
To control for this, I include the total number of listings by the seller in my dataset as a
covariate, as well as whether they posted a phone number and an address. All of these measures
track whether the seller is a professional car dealer or not. I report the results in column
(4). I find that although posting a phone number is valuable (perhaps because it facilitates
communication), both the number of listings and the address have negative coefficients. That
is, there is little evidence that buyers are willing to pay more to buy from a frequent lister
or a firm that posts its address. Again, the coefficients on text and photos remain large and
significant.
Finally, I try to test my hypothesis that text and photos matter because they inform potential
buyers about car attributes that are unobserved by the econometrician. To do this, I include
dummies for whether the car is under warranty, and has been certified by the seller as inspected.
Both of these variables should reduce the value of information, because the details of car
condition and history become less important if one knows that the car is under warranty or
has already been certified as being in excellent condition. In line with this idea, I include
interaction terms between the warranty and inspection dummies and the amount of text and
photos. The results in column (5) indicate that the interaction terms are significantly negative
as expected, while both the inspection and warranty significantly raise the expected price of
the vehicle. For cars that have neither been inspected nor are under warranty, the coefficients
on text and photos increase.
There are problems with a simple hedonic regression, and in order to deal with the problem
of bids being strategic and different from the underlying valuations, I will need a structural
13
model. I will also need to demonstrate that my measures of the quantity of information are
effective proxies for the content of that information. Yet the reduced form makes the point
that the amount of text and photos are positively related to auction price, and that the most
compelling explanation for this is that their content gives valuable information to potential
buyers.
4
Theory
Modeling demand on eBay is not a trivial task. The auction framework has a bewildering
array of institutional features, such as proxy bidding, secret reserves and sniping software.
With this in mind, it is critical to focus on the motivating question: how does seller revelation
of information through the auction webpage affect bidder beliefs about car value, and thereby
behavior and prices?
I make three important modeling choices. The first is to model an auction on eBay Motors as a
symmetric common value auction. In this model, agents have identical preferences, but are all
uncertain as to the value of the object upon which they are bidding. The bidders begin with
a common prior distribution over the object’s value, but then draw different private signals,
which generates differences in bidding behavior. This lies in contrast to a private values model,
in which agents are certain of their private valuation, and differences in bidding behavior result
from differences in these private valuations.
I believe that the common value framework is better suited to the case of eBay Motors than
the private values framework for a number of reasons. First, it allows bidders to be uncertain
about the value of the item they are bidding on, and this uncertainty is necessary for any model
that incorporates asymmetric information and the potential for adverse selection. Second, the
data support the choice of a common values model. I show this in the appendix, where I
implement the Athey and Haile (2002) test of symmetric private values against symmetric
common values, and reject the private value null hypothesis at the 5% level.12 Third, it
provides a clean framework within which one may think clearly about the role of the auction
webpage in this market. The auction webpage is the starting point for all bidders in an online
auction, and can thus be modeled as the source of the common prior that bidders have for the
object’s value. I can identify the role of information on eBay Motors by examining its effect
on the distribution of the common prior. Finally, though market participants on eBay Motors
12
The test is based on the idea that the Winner’s Curse is present in common values auctions, but not
in private values auctions. This motivates a test based on stochastic dominance relationships between bid
distributions as the number of bidders n, and thus the Winner’s Curse, increases.
14
will in general have different preferences, it may be reasonable to assume that those bidders
who have selected into any particular auction have similar preferences. This is captured in the
common values assumption.13
The second modeling choice is to use a modified version of the Bajari and Horta¸csu (2003)
model of late bidding on eBay. On eBay Motors, I observe many bids in the early stages of the
auction that seem speculative and unreflective of underlying valuations; while in the late stages
of the auction, I observe more realistic bids. With late bidding, bidders often do not have time
to best respond to opponent’s play. “Sniping” software can be set to bid on a player’s behalf
up to one second before the end of the auction, and bidders cannot best respond to these late
bids. Bajari and Horta¸csu (2003) capture these ideas in a two stage model, in which bidders
may observe each other’s bids in the early stage, but play the second stage as though it were
a sealed bid second price auction. I vary from their model by taking account of the timing of
bids in the late stage, since a bid will only be recorded if it is above the current price.14
Accounting for timing is important, as an example will make clear. Suppose that during the
early stage of an auction bidder A makes a speculative bid of $2000. As the price rises and it
becomes obvious this bid will not suffice, she programs her sniping software to bid her valuation
of $5600 in the last five seconds of an auction. Now suppose that bidder B bids $6000 an hour
before the end of the auction, and so when bidder A’s software attempts to make a bid on her
behalf at the end of the auction, the bid is below the standing price and hence not recorded.
The highest bid by bidder A observed during the auction is thus $2000. An econometrician
who treats an eBay auction as simply being a second price sealed bid auction may assume that
bidder A’s valuation of the object is $2000, rather than $5600. This will lead to inconsistent
parameter estimates. I show that regardless of bid timing, the final price in the auction with
late bidding is the valuation of the bidder with the second highest private signal. This allows
me to construct a robust estimation procedure based on auction prices, rather than the full
distribution of bids.
Lastly, I allow for asymmetric information, and let the seller privately know the realizations
of a number of signals affiliated with the value of the car. One may think of these signals as
describing the car history, condition and features. The seller may choose which of these signals
to reveal on the auction webpage, but since writing detailed webpages and taking photos is
costly, such revelations are each associated with a revelation cost. In line with my earlier
description of the institutional details of eBay Motors, all revelations made by the seller are
13
One could consider a more general model of affiliated values, incorporating both common and private value
elements. Unfortunately, without strong assumptions, such a model will tend to be unidentified.
14
Song (2004) also makes this observation, and uses it to argue that in the independent private values context
(IPV), the only value that will be recorded with certainty is that of the second highest bidder.
15
modeled as being credible. This assumption prevents the model from being a signaling model
in the style of Spence (1973).15 Instead, this setup is similar to the models of Grossman (1981)
and Milgrom (1981), in which a seller strategically and costlessly makes ex-post verifiable
statements about product quality to influence the decision of a buyer. In these models, an
unravelling result obtains, whereby buyers are skeptical and assume the worst in the absence
of information, and consequently sellers reveal all their private information.
My model differs in three important respects from these benchmarks. First, I allow for revelation costs. This limits the incentives for sellers to reveal information, and thus the unravelling
argument no longer holds. Second, the parties receiving information in my model are bidders,
who then proceed to participate in an auction, inducing a multi-stage game. Finally, I allow
the seller’s private information to be multidimensional. While each of these modifications has
received treatment elsewhere16 there is no unified treatment of revelation games with all these
features, and attempting a full analysis of the resulting multi-stage game is beyond the scope of
this paper. Instead I provide results for the case in which the relationship between the seller’s
private information and the car’s value is additively separable in the signals. This assumption
will be highlighted in the formal analysis below.
4.1
An Auction Model with Late Bidding
Consider a symmetric common values auction model, as in Wilson (1977). There are N
symmetric bidders, bidding for an object of unknown common value V . Bidders have a common
prior distribution for V , denoted F . Each bidder i is endowed with a private signal Xi , and
these signals are conditionally i.i.d., with common conditional distribution G|v. The variables
V and X = X1 , X2 · · · Xn are affiliated.17 The realization of the common value is denoted
v, and the realization of each private signal is denoted xi . The realized number of bidders
n is common knowledge.18 One may think of the bidders’ common prior as being based on
the content of the auction webpage. Their private signals may come from a variety of sources
15
In those games, the sender may manipulate the signals she sends in order to convince the receiver that she
is of high type. Here the sender is constrained to either truthfully reveal the signal realization, or to not reveal
it at all.
16
See for example Jovanovic (1982) for costly revelation, Okuno-Fujiwara, Postlewaite, and Suzumura (1990)
for revelations in a multi-stage game and Milgrom and Roberts (1986) for multidimensional signal revelation.
17
This property is equivalent to the log supermodularity of the joint density of V and X. A definition of log
supermodularity is provided in the appendix.
18
This assumption is somewhat unrealistic, as bidders in an eBay auction can never be sure of how many
other bidders they are competing with. The alternative is to let auction participants form beliefs about n, where
those beliefs are based on a first stage entry game, as in Levin and Smith (1994). But dealing with endogenous
entry in this way has certain problems in an eBay context (see Song (2004)), and thus I choose to go with the
simpler model and make n common knowledge.
16
such as private communications with the seller through e-mail or phone and the results of
inspections they have contracted for or performed in person.
Bidding takes place over a fixed auction time period [0, τ ]. At any time during the auction, t,
the standing price pt is posted on the auction website. The standing price at t is given by the
second highest bid submitted during the period [0, t). Bidding takes place in two stages. In
the early stage [0, τ − ), the auction takes the form of an open exit ascending auction. Bidders
may observe the bidding history, and in particular observe the prices at which individuals drop
out of the early stage. In the late stage [τ − , τ ], all bidders are able to bid again. This
time, however, they don’t have time to observe each other’s bidding behavior. They may each
submit a single bid, and the timing of their submission is assumed to be randomly distributed
over the time interval [τ − , τ ].19 If their bid bit is lower than the standing price pt , their bid is
not recorded. The following proposition summarizes the relevant equilibrium behavior in this
model:
Proposition 1 (Equilibrium without Revelation) There exists a symmetric Bayes-Nash
equilibrium in which:
(a) All bidders bid zero during the early stage of the auction.
(b) All bidders bid their pseudo value during the late stage, where their pseudo value is defined
by
v(x, x; n) = E[V |Xi = x, Y = x, N = n]
(2)
and Y = maxj6=i Xj is the maximum of the other bidder’s signals.
(c) The final price is pτ is given by
pτ = v(x(n−1:n) , x(n−1:n) ; n)
(3)
where x(n−1:n) denotes the second highest realization of the signals {Xi }.
The idea is that bidders have no incentive to bid a positive amount during the early stage of
the auction, as this may reveal their private information to the other bidders. Thus they bid
only in the late stage, bidding as in a second price sealed bid auction. The second highest bid
will certainly be recorded, and I obtain an explicit formula for the final price in the auction as
the bidding function evaluated at the second highest signal. This formula will form the basis
of my estimation strategy later in the paper. In the model thus far, though, I have not allowed
the seller to reveal his private information. I extend the model to accommodate information
asymmetry and seller revelation in the next section.
19
Allowing bidders to choose the timing of their bid would not change equilibrium behavior, and would
unnecessarily complicate the argument.
17
4.2
Information Revelation
Let the seller privately observe a vector of real-valued signals S = S1 · · · Sm with common
bounded support [s, s]. As with the bidder’s private information, these signals are conditionally
i.i.d with common distribution H|v and are conditionally independent of the bidder’s private
signals X1 · · · Xn . Let V and S = S1 · · · Sm be affiliated. The seller may report his signals to
the bidders prior to the start of the auction, and bidders treat all such revelations as credible.
The seller’s objective is to maximize his expected revenue from the auction. A (pure strategy)
reporting policy for the seller is a mapping R : Rm → {0, 1}m , where reporting the signal is
denoted 1 and not reporting is denoted 0. Letting s = s1 · · · sm be a realization of the signal
vector S = S1 · · · Sm , define I = #{i : Ri (s) = 1} as the number of signals reported by the
seller. Finally, let the seller face a fixed revelation cost ci for revealing the signal Si , and let
the associated cost vector be c. Revelation costs are common knowledge.
This setup generates a multi-stage game in which the seller first makes credible and public
statements about the object to be sold, and then bidders update their priors and participate
in an auction. Since each revelation by the seller is posted to the auction webpage, there
is a natural link between the number of signals I and my empirical measures of information
content, the number of photos and bytes of text on the webpage.
Define the updated pseudo value w(x, y, s; n) = E[V |X = x, Y = y, S = s, N = n] where
Y = maxj6=i Xj is the maximum of the other bidder’s signals. Then in the absence of revelation
costs, the equilibrium reporting policy for the seller is to reveal all his information:
Proposition 2 (Unravelling) For c = 0, there exists a sequential equilibrium in which the
seller reports all his signals (R(s) = 1 ∀s), bidders bid zero in the early stage of the auction,
and bid their updated pseudo value w(x, x, s; n) in the late stage.
This result seems counter-intuitive. It implies that sellers with “lemons” - cars with a bad
history or in poor condition - will disclose this information to buyers, which runs counter to
the intuition behind models of adverse selection. It also implies that the quantity of information
revealed on the auction webpage should be unrelated to the value of the car, since sellers will
fully disclose, regardless of the value of the car. Since I know from the hedonic regressions that
price and information measures are positively related, it suggests that the costless revelation
model is ill suited to explaining behavior in this market. Revealing credible information is
a costly activity for the seller, and thus sellers with “lemons” have few incentives to do so.
I can account for this by considering the case with strictly positive revelation costs, but this
generates a non-trivial decision problem for the seller. In order to make the equilibrium analysis
tractable, I make a simplifying assumption.
18
Assumption 1 (Constant Differences) The function w(x, y, s; n) exhibits constant differences in si for all (x, y, s−i ). That is, there exist functions ∆i (s1 , s0 ; n), i = 1 · · · m, such
that:
∆i (s1 , s0 ; n) = w(x, y, s−i , s1 ; n) − w(x, y, s−i , s0 ; n) ∀(x, y, s−i )
This assumption says that from the bidder’s point of view, the implied value of each signal
revealed by the seller is independent of all other signals the bidder observes.20 The extent to
which this assumption is reasonable depends on the extent to which car features, history and
condition are substitutes or complements for value. Under this assumption, one may obtain a
clean characterization of equilibrium.
Proposition 3 (Costly Information Revelation) For c > 0, there exists a sequential
equilibrium in which:
(a) The reporting policy is characterized by a vector of cutoffs t = t1 · · · tm with

1
Ri (s) =
0
if si ≥ ti
otherwise
where ti = inf {t : E [∆i (t, t0 ; n)|t0 < t] ≥ ci }.
(b) Bidders bid zero during the early stage of the auction, and bid
vR (x, x, sR ; n) = E[w(x, x, s; n)|{si < ti }i∈U ]
during the late stage, where sR is the vector of reported signals and U = {i : R(si ) = 0}
is the set of unreported signals.
(c) The final auction price is pτ = vR (x(n−1:n) , x(n−1:n) , sR ; n).
In contrast to the result with costless revelation, this equilibrium is characterized by partial
revelation, where sellers choose to reveal only sufficiently favorable private information. Bidders
(correctly) interpret the absence of information as a bad signal about the value of the car, and
adjust their bids accordingly. Then the number of signals I revealed by the seller is positively
correlated with the value of the car.
Corollary 1 (Expected Monotonicity) E[V |I] is increasing in I.
I prove the result by showing that the seller’s equilibrium strategy induces affiliation between
V and I. This result is useful for my empirical analysis, as it establishes a formal link between
20
A sufficient condition for the constant differences assumption to holdP
is that the conditional mean E[V |X, S]
is additively separable in the signals S, so that E[V |X = x, S = s] = m
j=1 fj (sj ) + g(x) for some increasing
real-valued functions fj and g.
19
the number of signals I, quantified in the number of photos and bytes of text on the auction
webpage, and the content of that information, the public signals S. It also provides a testable
prediction: that the prior mean E[V |I] should be increasing in the amount of information
posted. I now proceed to outline the strategy for estimating this auction model.
5
Auction Estimation
Estimating a structural model is useful here. First, I am able to account for the strategic
interaction between bidders and uncover the relationship between valuations and item characteristics, rather than price and characteristics. Second, I can test the model’s implications
precisely. The model predicts a positive relationship between the conditional mean E[V |I]
and I. This in turn implies that E[p|I] is increasing in I, but that positive relationship could
also hold because better informed bidders are less afraid of the Winner’s Curse and therefore
bid more.21 Estimating the structural model allows a test of the model prediction that is free
of strategic considerations on the part of bidders. Finally, and most important, structural
estimation permits simulation of counterfactuals. This will allow me to quantify the impact of
the auction webpage in reducing information asymmetries and adverse selection below.
Yet estimating a common values auction is a thorny task. There are two essential problems.
Firstly, a number of model primitives are latent: the common value V , and the private signals
X1 · · · Xn . Secondly, the bidding function itself is highly non-linear and so even in a parametric model computing the moments of the structural model is difficult and computationally
intensive. Addressing endogeneity in addition to the above problems is especially tricky. My
estimation approach is able to deal with all of these problems and remain computationally
tractable, and thus may be of independent interest. Two different approaches have been tried
in recent papers. Bajari and Horta¸csu (2003) employ a Bayesian approach with normal priors
and signals, and estimate the posterior distribution of the parameters by Markov Chain Monte
Carlo (MCMC) methods. Hong and Shum (2002) use a quantile estimation approach with
log normal priors and signals, and obtain parameter estimates by maximizing the resulting
quantile objective function.
My estimation approach, which is based on maximizing a pseudo-likelihood function, has a
number of advantages relative to these types of estimators. The main advantage lies in the
computational simplicity of my approach. I am able to show that my estimator may be
21
The Winner’s Curse is the result that bidders in a common value auction will be “cursed” if they bid their
conditional valuation of the object E[V |Xi ], as they will only win when their bid exceeds everyone else’s. In this
event, they also had the highest signal, which suggests that they were over-optimistic in their initial valuation.
Rational bidders therefore shade their bids down, always bidding below their conditional valuation.
20
maximized through a nested loop, in which the inner loop runs weighted least squares (WLS)
and the outer loop is a standard quasi-Newton maximization algorithm. For most applications,
the outer loop will search over a low dimensional space, while the inner loop may be of almost
arbitrarily high dimension since the maximizer may be computed analytically. This avoids the
curse of dimensionality, and allows me to include over thirty regressors in the structural model
while still maximizing the objective function in less than thirty minutes.22 By contrast, the
existing estimation techniques would require an MCMC implementation in a thirty dimensional
parameter space, and it would typically take days of computation to get convergence of the
chain to the stationary distribution of the parameters.23
A second advantage is that my estimation approach permits a semiparametric control function
method for dealing with endogeneity. Here I consider the case where precisely one variable is
endogenous and show that if the relationship between the endogenous variable and the source
of the endogeneity is monotone, a nonparametric first stage can be used to estimate a proxy
variable that controls for endogeneity. I note that the econometric theory given in Andrews
(1994a) guarantees the consistency and asymptotic normality of the resulting estimator, even
in the complicated non-linear setting of a common value auction.
The third advantage is eBay specific, and lies in the fact that I identify the model using only
variation in auction prices, the number of bidders n, and the covariates. This contrasts with
papers that use all bids from each auction, which can lead to misinterpretation. Identification
is also extremely transparent in this setup, which is not the case with the other estimators. I
now provide the specifics of the estimation approach.
5.1
Specification
The theory provides a precise form for the relationship between the final price in each auction
and the bidders’ priors and private signals. In order to link price to the auction covariates
such as item characteristics and information, I first specify a parametric form for the interim
prior distribution F |z and the conditional signal distribution G|v.24 I may then specify the
relationship between the moments of these distributions and auction covariates z. Let F |z
be the log-normal distribution, and let G|v be the normal distribution centered at v˜ = log v.
22
Most of these are fixed effects, but this approach could accommodate thirty continuous regressors.
This remark applies to the quantile estimation approach as well, since the objective function is not smooth
and therefore MCMC is the considered to be the best approach for maximizing it. See Chernozhukov and Hong
(2003) for details.
24
By “interim prior”, I mean the updated prior held by bidders after viewing the webpage but before obtaining
their private signal.
23
21
Then we have:
v˜ = µ + σεv ∼ N (µ, σ 2 )
xi |˜
v = v˜ + rεi ∼ N (˜
v, r2 )
where εv , εi are i.i.d standard normal random variables for all i.25 Three variables form the
primitives of the auction model: the interim prior mean µ, the interim prior standard deviation
σ, and the signal standard deviation r.
Next I link the primitives (µ, σ, r) to the auction covariates. As argued earlier, the information
posted on the auction webpage changes the common prior distribution over values for all
bidders. Consequently, I allow the mean and standard deviation of F , µ and σ, to vary with
auction covariates z. I include in z my empirical measures of information content, the number
of photos and bytes of text. The signal variance parameter r is treated as a constant, as the
private information is by definition orthogonal to the publicly available information captured
in the covariates. The chosen specification takes the index form:
µj = αzj
σj = κ(βzj )
where κ is an increasing function with strictly positive range, so that κ(x) > 0 ∀x.26 This
specification yields admissible values for σj .
5.2
Method
The above specification governs the relationship between the parameter vector θ = (α, β, r),
bidder prior valuations, and bidder signals. Prices are a complex function of these parameters,
since they are equal to the equilibrium bid of the bidder with the second highest signal, an
order statistic. Thus even though I have a fully specified parametric model for valuations
and signals, the distribution of prices is hard to determine. This prevents a straightforward
maximum likelihood approach. I can however compute the mean and variance of log prices
implied by the structural model, E[log p|n, zj , θ] and Ω[log p|n, zj , θ].27 Notice that these
predicted moments vary with the number of bidders n. Computing these moments allows me to
25
The choice of the log normal distribution for v is motivated by two considerations. First, all valuations
should be positive, so it is important to choose a distribution with strictly positive support. Second, the log prices
observed in the data are approximately normally distributed, and since the price distribution is generated by
the value distribution, this seems a sensible choice. The choice of a normal signal distribution is for convenience,
and seems reasonable given that the signals are latent and unobserved.
26
For computational reasons, κ(·) is based on the arctan function - specifics are given in the appendix.
27
Explicit formulae for these moments are to be found in the appendix.
22
estimate the model by pseudo-maximum likelihood(Gourieroux, Monfort, and Trognon 1984).
In this approach, I maximize a pseudo-likelihood function derived from a quadratic exponential
family. Since the observed price distribution is approximately log normal, and the log normal
distribution is quadratic exponential, I choose it as the basis of my pseudo likelihood function
and maximize the criterion function:
L(θ) = (−1/2)
J X
j=1
(log pj − E[log p|n, zj , θ])2
log(Ω[log p|n, zj , θ]) +
Ω[log p|n, zj , θ]
(4)
b is both consistent and asymptotiProvided that the model is identified, the PML estimator θ,
cally normal (Gourieroux, Monfort, and Trognon 1984).28 To see why the model is identified,
consider the case where there are no covariates apart from n, and the econometrician observes
the prices from repeatedly auctioning objects with values drawn from a common prior. The
number of bidders n in each auction is determined prior to the auction. The aim is to identify
the model primitives, the mean µ and standard deviation σ of the prior distribution, and the
signal standard deviation r. One may identify the prior mean µ from the mean prices of the
objects sold, and the variance in prices pins down σ and r though it does not separately identify them. For this, you need variation in the number of bidders n, which separately identifies
these parameters through variation in the Winner’s Curse effect.29
5.3
Computation
Due to the large number of covariates, the parameter space is of high dimension, and it is
possible that the problem could quickly become computationally intractable. Fortunately, the
following result eases the computational burden:
Proposition 4 (Properties of the Bidding Function) Let v(x, x; n, µ, σ, r) be the bidding
function under model primitives (µ, σ, r), and let v(x − a, x − a; n, z, µ − a, σ, r) be the bidding function when the signals of all bidders and the prior mean are decreased by a. Then
log v(x, x; n, µ, σ, r) = a + log v(x − a, x − a; n, µ − a, σ, r) and consequently:
E[log p|n, zj , α, β, r] = αzj + E[log p|n, z, α = 0, β, r]
(5)
Ω[log p|n, zj , α, β, r] =
(6)
Ω[log p|n, zj , α = 0, β, r]
28
Those familiar with the auctions estimation literature may be concerned about parameter support dependence, a problem noted in Donald and Paarsch (1993). It can be shown that under this specification the
equilibrium bid distribution has full support on [0, ∞), so this problem does not arise here.
29
The global identification condition is that if E[log p|n, zj , θ0 ] = E[log p|n, zj , θ1 ] and Ω[log p|n, zj , θ0 ] =
Ω[log p|n, zj , θ1 ] ∀(n, zj ) then θ0 = θ1 . I have numerically verified this condition for a range of parameter values.
23
This result is extremely useful. To see this, fix the parameters β and r, and consider finding
the parameter estimate α
b(β, r) that maximizes the criterion function (4). Using the result of
the above proposition, we can write this parameter estimate as:
α
b(β, r) = Argmin
α
J
X
j=1
1
(log pj − E[log p|n, zj , α = 0, β, r] − αz)2
Ω[log p|n, zj , α = 0, β, r]
which for fixed β and r can be solved by weighted least squares (WLS) with the dependent
variable yj = log pj − E[log p|n, zj , α = 0, β, r] and weights wj = 1/Ω[log p|n, zj , α = 0, β, r].
This allows a nested estimation procedure in which I search over the parameter space of (β, r),
using WLS to calculate α
b(β, r) at each step. Since I choose a specification in which most of
the covariates affect the prior mean and not the variance, this space is considerably smaller
than the full space of (α, β, r), and the computation is much simpler. Further computational
details are to be found in the appendix.
5.4
Endogeneity
In the above analysis, differences between observed prices and those predicted by the structural
model result from the unobserved deviations of the latent value and bidder signals from their
mean values. There is no unobserved source of heterogeneity between cars with identical
observed characteristics. Yet I know that in fact cars sold on eBay differ in many respects
that are not captured by the variables observed by the econometrician, such as in their history
or features. When sellers have favorable private information about the car they are selling,
they will reveal such information on the auction webpage. I capture the dollar value of the
webpage content in a variable ξ. But included in my covariates z are quantitative measures
of information, and these will be correlated with the omitted webpage content value ξ. This
may cause an endogeneity problem. This section investigates when this will be the case, and
provides a control-function based solution if needed.
In this section I will assume that I have a scalar endogenous information measure I.30 For
my application, I must choose between using the number of bytes of text and the number of
photos as this measure. I choose to use the text measure because I have a large number of
missing observations of the number of photos. Fortunately, the amount of text and photos are
highly correlated in the data and thus the amount of text will serve as a good measure of the
information content of the webpage by itself.31
30
I suspect that extending the approach to deal with a vector of endogenous variables is possible, but showing
this is beyond the scope of the paper.
31
The correlation is 0.35, which is higher than the correlation between age and mileage (0.26).
24
Partition the auction covariates so that zj = [Ij , zj0 ] where zj0 is the standardized characteristic
data observed by the econometrician, and Ij is the number of bytes of text on the auction
webpage. Now, following the theory, consider a new model specification in which the mean
and standard deviation of the interim prior distribution F |sR depend on the vector of reported
signals, sR :
where ξj =
P
sRi ∈z
/ j0
µj = φµ sRj = αzj + ξj
(7)
σj = φσ sRj =
(8)
κ (βzj )
φiµ si . In other words, ξ gives the contribution of the signals observed by
the bidders but not the econometrician to the mean of the interim prior. I will sometimes
refer to ξ as the content value of the webpage. I specify that the unobserved signals make no
contribution to the standard deviation, since it is unusual in demand estimation to account
for this possibility.32 At the cost of more notation these results can be extended to cover this
case.
Under the theoretical model, the information measure I is the number of signals si above a
threshold ti . It is therefore reasonable to believe that I is positively correlated with ξ. The
information measure I will thus be a valid proxy for the contribution of the webpage content
ξ to the interim prior mean valuation µ, under standard assumptions:
Assumption 2 (Redundancy) The information measure I is redundant in the true specification of the interim prior mean. That is, µj = E[log V |Ij , zj0 , ξj ] = E[log V |zj0 , ξj ].
Assumption 3 (Conditional Independence) The conditional mean E[ξ|Ij ] is independent
of the observed characteristics zj0 .
The redundancy assumption is quite plausible here, as I believe that it is the webpage content
rather than the quantity of information that matters for the interim prior valuation of bidders.
The conditional independence assumption is standard for a non-linear proxy, and essentially
says that when I is included as a regressor, the remaining covariates do not generate an
endogeneity problem. This sort of assumption is typical of the demand estimation literature,
in which only the potential endogeneity of price is typically addressed. With these assumptions
in place, the amount of information I - or more generally an unknown function of it - is a valid
proxy for the contribution of the omitted content to bidder priors. This justifies the estimation
approach in the above sections where I included information measures as regressors without
accounting for endogeneity.
32
This does not imply that the signals observed by bidders are not informative - it just implies that the prior
variance does not vary with the realization of the signals.
25
Arguing that the potentially endogenous variable I is simply redundant seems to make sense
here, but is clearly not an acceptable solution to the more general problem of endogeneity
in common value auction estimation. I next show how a control function approach can be
used to control for endogeneity when assumption 2 fails but assumption 3 is maintained so
that there is only one endogenous variable. Suppose that I have a valid instrument W for the
endogenous variable I, so that W is independent of ξ but correlated with I. I will need two
final assumptions:
Assumption 4 (Additive Separability) The endogenous variable I is an additively separable function of the observed characteristics z, instrument W , and the omitted variable ξ:
Ij = g(zj0 , Wj ) + h(ξj )
Assumption 5 (Monotonicity) The function h is strictly monotone.
These are relatively weak assumptions. For my particular application, additive separability is
plausible since the signals are conditionally independent, and so it is not unreasonable to believe
that I depends in a separable fashion on the observed characteristics z and the unobserved
content value ξ. Monotonicity is also reasonable, as when the seller has favorable information,
the theoretical model predicts that he will reveal it.
Now, define mj as the residual Ij − g(zj0 , Wj ). Then since mj is monotone in ξj , it is clear that
some function of mj could be used to control for ξj . I may estimate mj as the residuals from
a first stage nonparametric estimation procedure in which I regress Ij on the instrument Wj
and other car characteristics zj0 .33 I may then use the estimated residuals m
cj as a control for
ξ in the second stage regression. I summarize this result in a proposition:
Proposition 5 (Endogeneity) Under assumptions 3, 4 and 5, there exists a control function
f such that:
(a) E[log p|n, z, m, θ] = αz + E[log p|n, z, α = 0, β, r] + f (m)
(b) Ω[log p|n, z, m, θ] does not depend on ξ
Under technical conditions needed to ensure uniform convergence of the estimator, the PML
estimate θb obtained by maximizing the analogue of (4) under the above moment specification
remains both consistent and asymptotically normal. The relevant conditions are provided by
Andrews (1994a). Andrews (1994b) shows that if the first stage nonparametric estimation
33
This approach uses ideas seen in Blundell and Powell (2003), Newey, Powell, and Vella (1999) and Pinkse
(2000). I also consider a simpler first stage OLS procedure and present the results with this specification in the
results section below.
26
procedure is kernel based, then most of these conditions can be satisfied by careful choice of
the kernel, bandwidth and trimming. A more complete discussion of these technical issues is
deferred to the appendix.
To obtain an instrument, I exploit the fact that I have panel data. My instrument W is the
number of bytes of text in the description of the previous car sold by that seller. The idea is
that the quantity of information posted on the auction webpage for the previous car should
be independent of the value of the webpage content for the current car being sold. This relies
on the unobserved content of the auction webpages ξ being randomly assigned over time for a
given seller. This is reasonably plausible, as each car listed by a given dealer is likely to have
idiosyncratic features and history. On the other hand, the data shows a strong relationship
between the amount of information posted for the current car, I, and that for the previous car
W . This makes W a valid instrument. I estimate the fitted residuals m
b using kernel regression
with a multivariate Gaussian kernel, bandwidth choice by cross-validation and trimming as in
Andrews (1994b). I implement the control function f as a second-order polynomial in m.
b 34
Regardless of whether or not I is endogenous in the econometric sense, the control function
f (m) should be a better proxy than I for ξ, as it is orthogonal to the contribution of observed
characteristics z 0 and firm specific effects captured in W that are included in I but irrelevant
for ξ. My model thus predicts that the control function will be significant in the regression.
In the following section, I present the results of tests for significance and analyze the results of
the structural estimation.
6
Results
The results of the demand estimation follow in Tables 3, 4, 5 and 6, to be found in the
appendix.35 In the first table, I consider estimation of demand without controlling for endogeneity. As noted earlier, this approach will be valid under assumptions 2 and 3, in which
case the number of bytes of text will be a valid proxy for the unobserved webpage content.
I consider five specifications, corresponding to those given in the hedonic regressions earlier
in the paper. Throughout this section, one should note that model and title fixed effects are
included but not reported.
34
As is usual with control function approaches, one cannot be sure what the appropriate form of the control
function is, and so a flexible function is used. I have verified that the pseudo log likelihood does not change
significantly with the use of higher order or orthogonal (Legendre) polynomials, and so this simpler quadratic
model was chosen.
35
In all cases, standard errors are obtained from estimates of the asymptotic variance-covariance matrix. I
do not account for first stage error in constructing the standard errors for the parameters estimated using the
control function.
27
The coefficients on µ give the estimated relationship between the prior valuation and the
covariates. The coefficients on logged regressors may be seen as elasticities, while a one unit
change in an unlogged regressor i has a 100αi % effect on the prior valuation. It is immediately
apparent that age and mileage have significant effects on valuation in all specifications. Ignoring
the curvature introduced by the age squared term, an additional year of age is expected to
decrease bidder’s valuation by 21%, while every percentage increase in the mileage implies an
approximately 0.125% decrease in the price.
As in the hedonic regressions, the effect of the information measures on µ are significant in all
specifications and of large magnitude. I find that each additional percentage of text implies a
percentage increase of between 0.047% and 0.061% in the price (ignoring the final specification,
which includes interactions). For a typical car in the dataset, this implies that a percentage
increase in the amount of text supplied is associated with an increase in the price of about $5,
which is a big effect. But when one thinks of the range of seller revelations possible, including
important details such as car features and history, this is not really that surprising. There is
also a positive and highly significant relationship between the number of photos and the prior
valuation. I find that each photo is associated with an approximately 1.8% increase in the
prior valuation, which amounts to $180 for a typical car in my dataset. These results are as
predicted in Corollary 1, and therefore consistent with the theoretical model.
The additional covariates included in specifications (2)-(5) have coefficients of similar size and
magnitude to those in the hedonic regressions. Of interest is the sizable coefficient on featured
listings, which imply that featured cars are valued by buyers 19% more. Since these returns
vastly outstrip the costs of such a listing, one should be concerned about endogeneity. I do not
include this regressor in later estimations. Finally, I find that as before, the coefficient on the
interactions between the warranty and inspection dummies and my information measures are
significant and negative. This is consistent with the idea that the value of webpage content
such as vehicle history and photos is less valuable while the vehicle is still under warranty.
The second half of the table on the following page contains the coefficients on σ and the
constant bidder signal standard deviation r. These are harder to interpret. Note firstly that
the coefficient on text size is not significant, suggesting that the text does little to reduce prior
uncertainty about the quality of the car. The remaining coefficients for σ are significant at
the 5% level.36 To interpret the coefficients, I turn to the marginal effects. A extra year of
age is associated with a 0.013 increase in the standard deviation of the interim prior, while an
additional percentage of text is associated with a 0.00007 decrease in that deviation. Photos do
36
The link function used to convert rIN DEX into r implies that the T-test here is against the null that
r = 1.25. So the estimate for r is relatively precise, even though rIN DEX has a large standard error.
28
far more to reduce uncertainty, with each additional photo associated with a 0.0067 decrease in
the interim prior deviation. The photo content of auction webpages thus improves the precision
of bidder’s prior estimates and help them to avoid the winner’s curse.
One may wish to quantify the magnitude of this winner’s curse effect. To get at this I need
the estimated marginal effect of σ on price. I find that an increase of 1 standard deviation in
the prior uncertainty is associated with a 10% decrease in price. Thus each additional photo,
through decreasing the prior uncertainty, is expected to lead to a 0.067% increase in price, or
about $7 for a typical car. This effect, it is clear, is dwarfed by the direct effect of the photo
content. I can also use the estimates of r and σ to back out how heavily bidders will weight
their private signal as opposed to the public information in forming their posterior estimate of
car value. The relevant statistic is the ratio r/(r + σ), which indicates the weight on the public
information. This is estimated to be around 0.6 in all specifications, indicating that private
communications between buyers and sellers, while important, are less heavily weighted than
webpage content in forming posterior valuations.
In Table 4, I examine how these effects vary for different models of car. I group cars into
three groups, one consisting of “classic” cars such as the Mustang and Corvette, one consisting
of “reliable cars” such as the Honda Accord and Civic, and one consisting solely of pickup
trucks (such as the Ford F Series and GM Silverado). The vehicles in the “classic” group are
considerably older than those in the other two groups, at an average of 24 years old versus 10
years for the reliable cars and 15 for the pickup trucks. A number of differences arise. The
predicted relationship between mileage, age and price varies for the three groups. The difference
is especially marked in the case of classic cars, where mileage has a considerably strongly
negative effect. This may be because vintage cars in near mint condition command much
higher premiums. I also find differences in the coefficient on transmission, which presumably
reflects a preference for manual transmission when driving a Corvette or Mustang, but not
when driving a pickup.
Most important, I find that the coefficients on the information measures vary considerably.
For classic cars, where vehicle history, repair and condition are of great importance, the text
size and photo coefficients are both large. On the other hand, for the reliable and largely
standardized cars such as the Accord and Toyota, these effects are much less. The coefficients
for pickups fall somewhere in between, perhaps because pickups have more options (long bed,
engine size) for a given model, and more variation in wear-and–tear than do the reliable cars.
I also find that the prior standard deviation varies considerably among groups, even after
accounting for age, text and photos. There is considerable prior uncertainty about the value
of classic cars, and far less for reliable cars, which makes sense. I do find though that the
29
uncertainty is quickly increasing in age for reliable cars, which is somewhat surprising. This
may be a local effect, which cannot be extrapolated beyond a neighborhood of the “mean car”.
Finally, I find that the weighting ratio between public and private information is similar for
classic cars and pickups, at around 0.6, but is higher for reliable cars at around 0.65. This
makes sense since these cars have less idiosyncratic features and bidders will therefore weight
private signals less heavily.
In Table 5, I present a comparison of the outcomes of the structural regression with and without a non-linear control function (modeled as a quadratic). The second specification gives
the control constructed with a non-parametric first stage and bandwidth h chosen by cross
validation. The third and fourth specifications are a robustness check, showing that the coefficients remain similar when I vary the bandwidth. The final specification considers a control
function constructed with an OLS first stage, for comparison. The number of observations is
smaller here (around 7000, as opposed to 35000 for the preceding regressions). This is because
construction of the instrument requires a panel of at least two observations for any given seller,
and the first observation of any panel is dropped due to lack of an instrument. In all specifications I use the log text size as my information measure, using only one such measure because
I only have an instrument for this variable.
One of the predictions of the theory is that the amount of information is an endogenous
variable, in that it is chosen strategically.37 This prediction is validated here, where I find that
the controls are jointly significant in all specifications. For example, I conduct a likelihood
ratio test on the exclusion of all controls, using the log likelihoods from the first and second
specifications. I compute the likelihood ratio test statistic LR = 19.88, which exceeds the
chi-squared critical value χ20.999 = 13.81 at the 0.1% level and thus conclude that the controls
are jointly significant. After including the control function, I find a corresponding decrease in
the coefficient on text size. It is somewhat surprising though that it remains significant and
positive. I explore this in more detailed regressions below. Finally, note that the remaining
coefficients remain largely unchanged after introducing the control function. This makes sense
since the control is orthogonal to the other characteristics z 0 by construction.
I consider a specification with controls and different car groups in Table 6. This specification
shows that the surprisingly large coefficient on log text, even after including controls, in Table
5 was due to the classic car group. For the other two car groups, the effect of the amount
of text is statistically indistinguishable from zero, after including controls. For both of these
groups, the controls show up as jointly significant. This validates the model prediction that it
37
Though it need not cause an endogeneity problem in the econometric sense - see the discussion in the section
on endogeneity.
30
is webpage content, rather than the amount of information that matters.
Yet for classic cars, both the controls and the amount of text are significant and large in
magnitude. A possible explanation for this lies in the nature of the instrument used. In order
for my instrument to be valid, I need random assignment of the content value ξ across cars
sold by the same seller. For car dealerships, who typically deal in high volume cars including
pickups and reliable cars, this assumption is reasonable. On the other hand, many of the sellers
of classic cars on eBay buy them elsewhere and restore them. In such a case, much of the value
of the car is wrapped up in the restoration process, and the unobserved content ξ will have a
large seller-specific term. The coefficient on log text may be picking up this effect.
The main results are as follows. First, the predictions of the costly revelation model hold
up in the data, across all specifications. Second, the fact that logtext is not significant after
controlling for endogeneity in two of the three specifications suggests that the amount of text
proxies for webpage content, rather than having any independent effect of its own. Third, I
find that webpage content has an important role in explaining prior valuations, which suggests
that seller revelation is important for informing bidders in this market.
7
Counterfactual Simulation
One of the strengths of structural estimation is the ability to perform counterfactual simulations
of market outcomes. In this section I return to the idea that motivated the paper, and quantify
the magnitude by which seller revelations through the auction webpage help to reduce the
potential for adverse selection. My tool in this endeavor is a stark counterfactual: a world in
which eBay stops sellers from posting their own information on the auction webpage, so that
only basic and standardized car characteristic data is publicly available.
This is hardly an idle comparison. Local classified advertisements typically provide only basic
information, while even some professional websites do not allow sellers to post their own
photos.38 In the case of local purchases, of course, potential buyers will view the cars in
person and so their private signals will be much more precise. This is typically not the case on
eBay Motors. I will show that even when private signals reflect the true value of the vehicle,
the less precise prior valuations held by bidders in the counterfactual world will lead them to
systematically underbid on “peaches” and overbid on “lemons”. Relative to the counterfactual
then, seller revelations through the auction webpage help to limit differences between prices
and valuations, and reduce adverse selection.
38
The South African version of Autotrader, autotrader.co.za, is such an example. Even on large online websites
such as cars.com and autobytel.com, it is unusual to find multiple photos for a vehicle.
31
Formally, let the data generating process (DGP) be as specified in the structural model presented earlier. For simplicity, I assume throughout this section that there is no unobserved
heterogeneity or endogeneity, so that I have access to all the information needed to simulate the
DGP. Since bidders in fact learn more from the auction webpage than I capture in my coarse
information measures, this assumption will lead me to underestimate the role of seller revelation in my simulation results. Recall that values are log normally distributed, so that v˜ = log v
p
has normal distribution with mean µ = E[˜
v |I, z 0 ] and standard deviation σ = V ar[˜
v |I, z 0 ].
Bidders independently observe unbiased and normally distributed private signals of the log
value v˜, with signal standard deviation r.
Now consider two regimes. In the true regime, bidders observe the auction webpage and
form a prior valuation based on the standardized characteristic data z 0 and the amount of
information I. Their prior is correct in equilibrium, and thus parameterized by µ and σ.
In the counterfactual regime, the auction webpage contains only the standardized data and
so bidders have a less informative prior. This prior is log normal, and parameterized by
p
v |z 0 ]. Bidders still obtain independent and unbiased private
µc = E[˜
v |z 0 ] and σ c = V ar[˜
signals in both regimes.
To see how prices respond to seller revelation in the equilibrium and in the counterfactual
case, I simulate the bidding function and compute expected prices under both regimes for a
random sample of 1000 car auctions in my dataset. For the equilibrium regime, this is relatively
straightforward. The estimated structural parameters imply estimates of the model primitives
µ, σ and r for each data point, and I can compute the expected price E[p|I, z 0 ] predicted by the
model. To get the expected price under the counterfactual, E[pc |I, z 0 ], I estimate µc and σ c .
I do this by integrating out I from E[˜
v |I, z 0 ] and V ar[˜
v |I, z 0 ] over the conditional distribution
of I given z 0 . This gives me the counterfactual prior, and allows me to simulate the bidding
function for any signal realization xi . I obtain the expected price E[pc |I, z 0 ] by integrating over
the distribution of ordered signal realizations x(n−1:n) specified by the DGP. Since it will be
useful to compare relative prices and values across auctions, I specify a baseline price. I define
the baseline price as the expected price E[pb |z 0 ] which would obtain if the counterfactual prior
specified by µc and σ c was in fact correct, so that µc = µ and σ c = σ. One may think of this
as the case in which the seller is selling a car whose condition is “average” in the sense that
his equilibrium revelations would not cause bidders to revise their priors at all. Notice that
under the DGP the distribution of values depends on I, and thus so do the private signals and
the expected prices. This is the sense in which private signals reveal the true value of the car
even in the counterfactual world.39
39
Additional details about the simulation are given in the appendix.
32
Rel. Price !%"
15
10
5
!15
!10
!5
!5
5
10
15
Rel. Value !%"
!10
!15
Figure 5: Simulation Results Relative value is defined as a function of the ratio E[V |I, z 0 ]/E[V |z 0 ],
so that cars with a high relative value are revealed through seller revelations to be “peaches”, while the
opposite implies the car is a lemon. The blue dots show the percentage by which the simulated prices
for these cars exceed a baseline price E[pb |z 0 ] under the true regime. The green dots show the relative
price under the counterfactual in which sellers cannot reveal their private information on the auction
webpage, but buyers still get accurate private signals.
The results are graphically depicted in Figure 5. On the x-axis, I have the relative value of
the car, which I define as the percentage by which the informed prior valuation E[V |I, z 0 ]
exceeds the uninformed prior E[V |z 0 ]. A simple characterization of this is that those cars with
relative value greater than zero are “peaches”, while those with relative value less than zero are
“lemons”. On the y-axis, I have the relative price of the car, which I define as the percentage
by which the expected price E[p|I, z 0 ] or E[pc |I, z 0 ] exceeds the baseline price E[pb |z 0 ]. Since
the baseline price is that for an average car with characteristics z 0 , relative prices should be
positive when the car is better than average (i.e. a peach), and negative when the car is worse
than average (i.e. a lemon). The points in blue are expected prices under the equilibrium
model, while those in green are from the counterfactual simulation.
It is clear after examining Figure 5 that a linear model would describe the relationship between
relative value and relative price quite well in both regimes. Fitting such a model yields an
estimated slope coefficient for the equilibrium model of 1.014., while that for the counterfactual
is 0.609.40 This implies a seller with a car revealed to be worth 10% more than the baseline
can expect to fetch 10.1% more for his car than the baseline price when sold on eBay Motors.
Thus a seller with a peach can post information and inform buyers of the car’s quality and
40
Both are estimated extremely precisely, with t-statistics of 413 and 121 respectively.
33
hence obtain a price premium commensurate with the value of the car.41 By contrast, under
the counterfactual, that same car would fetch only 6% more than the baseline, because the
prior value that potential buyers place on the car is the baseline value. Although bidders
will on average receive favorable private signals indicating that the quality of the car is high,
such signals receive limited weight because they are noisy. The overall effect is that without
revelation on the auction webpage, the seller is on average only able to extract 61% of the
additional value of his vehicle in revenue.
These simulation results make clear the role that public seller revelations can play in reducing
adverse selection in this market. Whenever sellers with high quality cars are unable to extract
a commensurate price premium from buyers because of information asymmetries, there is
the potential for adverse selection. In the counterfactual regime without revelation, the gap
between relative value and relative price is nearly 40%, and this potential is high. It is clear
from my simulations then that seller revelations reduce the potential for adverse selection
significantly.
8
Conclusion
In a world in which ever more esoteric items are sold online, it is important to understand
what makes these markets work. This paper shows that information asymmetries in these
markets can be endogenously resolved, so that adverse selection need not occur. The required
institutional feature is a means for credible information revelation. With this in place, sellers
have both the opportunity and the incentives to remedy information asymmetries between
themselves and potential buyers.
Where such mechanisms for credible information revelation exist, it is clear from my results
that these revelations can be important determinants of buyer behavior and thus prices. The
theory developed in this paper suggests that in the face of revelation costs, sellers will reveal
only the most favorable of their private information. It follows that quantitative measures of
information, such as those provided in this paper, will have predictive power for prices. Future
research could see whether this holds true in other settings, for if it does, this provides a useful
set of proxies for unobserved differences in heterogeneous goods markets with information
asymmetries.
41
In fact, the seller will do slightly better because the additional information reduces uncertainty and the
Winner’s Curse, and thereby raises prices.
34
References
Akerlof, G. A. (1970): “The Market for Lemons: Quality Uncertainty and the Market
Mechanism,” Quarterly Journal of Economics, 84(3), 488–500.
Andrews, D. W. K. (1994a): “Asymptotics for Semiparametric Econometric Models via
Stochastic Equicontinuity,” Econometrica, 62(1), 43–72.
(1994b): “Nonparamatric Kernel Estimation for Semiparametric Models,” Econometric Theory, 10.
Athey, S. (2002): “Monotone Comparative Statics under Uncertainty,” Quarterly Journal of
Economics, 117(1), 187–223.
Athey, S., and P. Haile (2002): “Identification of Standard Auction Models,” Econometrica,
70(6), 2107–2140.
Athey, S., J. Levin, and E. Seira (2004): “Comparing Open and Sealed-Bid Auctions:
Theory and Evidence from Timber Auctions,” mimeo, Stanford University.
Bajari, P., and A. Hortac
¸ su (2003): “The winner’s curse, reserve prices and endogenous
entry: empirical insights from eBay auctions,” Rand Journal of Economics, 34(2), 329–355.
Blundell, R., and J. Powell (2003): “Endogeneity in Nonparametric and Semiparametric
Regressions Models,” in Advances in Economics and Econometrics, ed. by M. Dewatripont,
L. P. Hansen, and S. J. Turnovsky. Cambridge University Press.
Chernozhukov, V., and H. Hong (2003): “An MCMC approach to classical estimation,”
Journal of Econometrics, 115, 293–346.
Chiappori, P.-A., and B. Salanie (2000): “Testing for Asymmetric Information in Insurance Markets,” Journal of Political Economy, 108(1), 56–78.
Cohen, A., and L. Einav (2006): “Estimating Risk Preferences from Deductible Choice,”
forthcoming in American Economic Review.
Donald, S. G., and H. J. Paarsch (1993): “Piecewise Pseudo Maximum Likelihood Estimation in Empirical Models of Auctions,” International Economic Review, 34(1), 121–148.
Gourieroux, C., A. Monfort, and A. Trognon (1984): “Pseudo Maximum Likelihood
Methods: Theory,” Econometrica, 52(3), 681–700.
35
Grossman, S. J. (1981): “The Informational Role of Warranties and Private Disclosures,”
Journal of Law and Economics, 24(3), 461–483.
Haile, P., H. Hong, and M. Shum (2003): “Nonparametric tests for common values at
first-price sealed bid auctions,” NBER Working Paper 10105.
Hong, H., and M. Shum (2002): “Increasing Competition and the Winner’s Curse: Evidence
from Procurement,” Review of Economic Studies, 69, 871–898.
Houser, D., and J. Wooders (2006): “Reputation in Auctions: Theory and Evidence from
eBay,” Journal of Economics and Management Strategy, 15(2), 353–370.
Jovanovic, B. (1982): “Truthful Disclosure of Information,” Bell Journal of Economics,
13(1), 36–44.
Krasnokutskaya, E. (2002): “Identification and Estimation in Highway Procurement Auctions under Unobserved Auction Heterogeneity,” mimeo, University of Pennsylvania.
Levin, D., and J. L. Smith (1994): “Equilibrium in Auctions with Entry,” American Economic Review, 84(3), 585–99.
Linton, O., E. Maasoumi, and Y.-J. Whang (2005): “Consistent Testing for Stochastic
Dominance under General Sampling Schemes,” Review of Economic Studies, 72, 735–765.
Melnik, M., and J. Alm (2002): “Does a Seller’s Ecommerce reputation matter? Evidence
from eBay Auctions,” Journal of Industrial Economics, L(3), 337–349.
Milgrom, P. (1981): “Good News and Bad News: Representation Theorems and Applications,” Bell Journal of Economics, 12(2), 380–391.
Milgrom, P., and J. Roberts (1986): “Relying on the information of interested parties,”
Rand Journal of Economics, 17(1).
Milgrom, P., and R. J. Weber (1982): “A Theory of Auctions and Competitive Bidding,”
Econometrica, 50(5), 1089–1122.
Newey, W. K., J. L. Powell, and F. Vella (1999): “Nonparametric Estimation of Triangular Simultaneous Equations Models,” Econometrica, 67(3), 565–603.
Okuno-Fujiwara, M., A. Postlewaite, and K. Suzumura (1990): “Strategic Information
Revelation,” Review of Economic Studies, 57(1), 25–47.
36
Pinkse, J. (2000): “Nonparametric Two-Step Regression Estimation when Regressors and
Error are Dependent,” Canadian Journal of Statistics, 28(2), 289–300.
Politis, D. N., J. P. Romano, and M. Wolf (1999): Subsampling. Springer, New York.
Resnick, P., and R. Zeckhauser (2002): Trust Among Strangers in Internet Transactions:
Empirical Analysis of eBay’s Reputation Systemvol. 11 of Advances in Applied Microeconomics, chap. 5. Elsevier Science.
Shin, H. (1994): “News Management and the Value of Firms,” Rand Journal of Economics,
25(1), 58–71.
Song, U. (2004): “Nonparametric Estimation of an eBay Auction Model with an Unknown
Number of Bidders,” Working Paper, University of British Columbia.
Spence, M. A. (1973): “Job Market Signalling,” The Quarterly Journal of Economics, 87(3),
355–74.
Wilson, R. (1977): “A Bidding Model of Perfect Competition,” Review of Economic Studies,
4, 511–518.
37
9
Appendix
A. Proof of Proposition 1
The first two results follow from Proposition 1 in Bajari and Horta¸csu (2003), after noting
that the two auction models are strategically equivalent. To obtain the final result, order the
bidders by the realization of their signals beginning with the bidder with the highest signal,
bidder 1. Now, let bidder 2 submit his bid in the late stage at randomly determined time
t2 ∈ [τ − , τ ] . Since bids are monotone in the signals, and the standing price is the second
highest bid submitted on [0, t2 ), under the equilibrium strategies the standing price pt2 cannot
exceed v(x(n−2:n) , x(n−2:n) ; n). Thus the bid of bidder 2, v(x(n−1:n) , x(n−1:n) ; n), will exceed the
standing price and be recorded. At some point t1 in [τ − , τ ], the bid of bidder 1 will likewise
be recorded. Thus at the end of the auction, the final price will be the second highest of the
recorded bids, which is v(x(n−1:n) , x(n−1:n) ; n).
B. Proof of Proposition 2
Sequential equilibrium requires that bidders have consistent beliefs and that their behavior is
sequentially rational. So consider any equilibrium reporting policy R. On path, consistency
requires that bidders believe that reported signals SR are equal to their reports sR ; and that
unreported signals SU are consistent with the reporting policy, so R(S) = r. Now, a report
vector r is off-path if there does not exist a signal realization s such that R(s) = r. In that
case, consistency still requires that bidders believe that reported signals SR are equal to their
reports sR , but places limited restrictions on the unreported signals. I specify that these
beliefs are Si = s ∀i ∈ U , so that bidders believe the worst of off-path unreported signals.
These beliefs satisfy consistency. Now, the symmetric strategies in which bidders bid zero
in the early stage of the auction and bid E[w(x, x, s; n)|R(s) = r, SR = sR ] (on path) or
E[w(x, x, s; n)|SR = sR , SU = s] (off path) in the late stage are mutual best responses. No
bidder has strict incentive to deviate in the early stage. In the late stage, bidders condition
on the revealed information sR and make (correct) inferences about the unrevealed signals
based on the seller’s equilibrium reporting policy. Their play satisfies sequential rationality.
To complete the equilibrium construction, I must show that the reporting policy Ri (s) = 1 ∀i
is optimal for the seller. Notice that for any deviation R0 , there must exist signal realizations
s with Ri0 (s) = 0. But for such realizations, the seller will expect to receive (weakly) less
revenue than under the equilibrium reporting policy, since the bids under R0 take the form
E[w(x, x, s; n)|SR = sR , sU = s] and this is weakly less than the equilibrium bid w(x, x, s; n).
38
C. Proof of Proposition 3
I begin with a useful lemma.
Lemma 1 Let U be a subset of 1 · · · m that includes element i, and let U−i be the same set
without element i. Then:
E w(x, x, s; n){sj < tj }j∈U−i − E [w(x, x, s; n)|{sj < tj }j∈U ] = E ∆i (si , s0i ; n)s0i < ti
Proof:
E w(x, x, s; n){sj < tj }j∈U−i −E [w(x, x, s; n)|{sj < tj }j∈U ]
= E w(x, x, s; n) − E [w(x, x, s; n)|si < ti ]{sj < tj }j∈U−i
= E E w(x, x, s−i , si ; n) − w(x, x, s−i , s0i ; n)s0i < ti {sj < tj }j∈U−i
= E E ∆i (si , s0i ; n)|s0i < ti {sj < tj }j∈U−i
= E ∆i (si , s0i ; n)s0i < ti
where the final line follows by Assumption 1.
Now, to prove the proposition, let bidders have beliefs as specified in the proof of Proposition
2 above. Let the seller’s reporting policy be as in the proposition. As before, the symmetric
strategies where bidders bid zero during the early stage of the auction and E[w(x, x, s; n)|R(s) =
r, SR = sR ] in the late stage are mutual best responses (all points are on path). Under the
sellers’ reporting policy, I may write E[w(x, x, s; n)|R(s) = r, SR = sR ] as vR (x, x, sR ; n) =
E[w(x, x, s; n)|{si < ti }i∈U ]. It remains to show that the seller’s strategy is optimal. To this
end, consider a deviation. Under the constant differences assumption, it will suffice to show
that for all realizations of the signal vector s, there is no signal si for which a deviation in
R(si ) is profitable. So consider revealing si < ti for some i. The payoff to deviation depends
on the seller’s expected revenue, and is given by:
i
h h
i
π =E E vR (x, x, sU−i ; n) − vR (x, x, sU ; n)X (n−1:n) = x S = s − ci
h h i
i
=E E E w(x, x, s; n)|{sj < tj }j∈U−i − E [w(x, x, s; n)|{sj < tj }j∈U ]X (n−1:n) = x S = s − ci
h h i
i
= E E E ∆i (si , s0i ; n)s0i < ti X (n−1:n) = x S = s − ci
= E ∆i (si , s0i ; n)|s0i < ti − ci
where the third line follows by Lemma 1, and the fourth by Assumption 1. Now since ti =
inf {t : E [∆i (t, t0 ; n)|t0 < t] ≥ ci }, and si < ti , this expression is negative and thus the deviation
39
is unprofitable. It can similarly be proved that the opposite deviation (not revealing si > ti )
is unprofitable. Hence the seller’s reporting policy is a best response to the bidder’s bidding
strategies. Finally, part (iii) follows immediately from the proof of proposition 1.
D. Proof of Corollary 1
By Bayes Rule:
Z
E[V |I] =
Z
vf (v|I)dv =
g(I|v)
vR
dv =
g(I|y)dF (y)
Z
v`(v, I)dv
One may show that `(I, v) is log supermodular (LSPM) - see below. It follows immediately
that v`(l, v) is also LSPM. But then the right hand side has the form EV [h(v, I)] where h(v, I)
is LSPM, and from the results in Athey (2002) it follows that EV [h(v, I)] is increasing in I.
This establishes the result.
E. Log Supermodularity of `(I, v)
A real-valued function g(x, y) : Rm+n → R is said to be LSPM if for all (x1 , y1 ) and (x2 , y2 ):
g(x1 ∧ x2 , y1 ∧ y2 )g(x1 ∨ x2 , y1 ∨ y2 ) ≥ g(x1 ∧ x2 , y1 ∨ y2 )g(x1 ∨ x2 , y1 ∧ y2 )
where ∨ is the component-wise minimum operator, and ∧ is the component-wise maximum
operator. Since `(I, v) is two-dimensional, it will suffice to prove that for v1 < v2 and I1 < I2 ,
we have:
`(v1 , I1 )`(v2 , I2 ) ≥ `(v1 , I2 )`(v2 , I1 )
Let pi (v) = 1−H(ti |v). By the affiliation of Si and V for all i, it follows that pi (v) is increasing
in v ∀i. Let r be a vector of reports and let ||r|| = #{i : ri = 1}. Then we have:
!
g(I|v) =
X
Y
r:||r||=I
ri =1
pi (v)
Y
(1 − pi (v))
ri =0
where I use the conditional independence of the signals Si to express the RHS as products.
Since the denominators on both sides cancel, it will suffice to prove that g(I1 |v1 )g(I2 |v2 ) ≥
40
g(I1 |v2 )g(I2 |v1 ). Take the LHS and expand it:

X
Y
r:||r||=I1
ri =1
LHS = 
=
M X
N
X
! 
X
(1 − pi (v1 ))  
ri =0
r:||r||=I2
Y
ri =1
pi (v2 )
Y
!
(1 − pi (v2 )) 
ri =0


Y

j=1 k=1
pi (v1 )
Y
pi (v1 )
rij =1
Y
(1 − pi (v1 ))
rij =0
Y
pi (v2 )
Y
(1 − pi (v2 ))
rik =0
rik =1
where j = 1 · · · M index the IS1 elements with ||r|| = I1 and k = 1 · · · N index the IS2
elements with ||r|| = I2 . Now expand and index the RHS in an identical fashion, and compare
the jk-th elements. After canceling identical terms on both sides, the result is:
Y
pi (v2 ) (1 − pi (v1 )) ≥
Y
pi (v1 ) (1 − pi (v2 ))
rij =0,rik =1
rij =0,rik =1
This inequality holds by the monotonicity of pi (v) ∀i, since that implies pi (v2 ) > pi (v1 ) and
1 − pi (v1) > 1 − pi (v2). But then since the inequality holds for all terms jk in the sum, it
holds for their summation as well. This proves the log supermodularity of `(I, v).
F. Proof of Proposition 4
By definition, v(x, x; n, µ, σ, r) = E[V |Xi = x, Y = x, N = n]. Condition on all other signals,
so that we have:
v(x, x; n, µ, σ, r) = EX−i |Y <x [V |Xi = x, X−i = x−i , N = n]
"
(
#
Pn
2 )
rµ + σ i=1 xi
1
rσ
= EX−i |Y <x exp
+
Xi = x, X−i = x−i , N = n
r + nσ
2 r + nσ
"
(
#
Pn
2 )
r(µ − a) + σ i=1 (xi − a) 1
rσ
= EX−i |Y <x exp a +
+
Xi = x, X−i = x−i , N = n
r + nσ
2 r + nσ
"
(
#
Pn
2 )
r(µ
−
a)
+
σ
(x
−
a)
1
rσ
i
i=1
= ea EX−i |Y <x exp
+
Xi = x, X−i = x−i , N = n
r + nσ
2 r + nσ
= ea v(x − a, x − a; n, µ − a, σ, r)
where the second line follows from the posterior mean and variance of log v given normal
unbiased signals {xi }, and the fourth line follows on noting that ea is a constant and thus can
be taken outside of the expectation. Taking logs on both sides, we get log v(x, x; n, µ, σ, r) =
a + log v(x − a, x − a; n, µ − a, σ, r).
To get equation (5), note that E[log p(n, µ, σ, r)] = E[log v(x(n−1:n) , x(n−1:n) , n, µ, σ, r)]. It
follows that E[log v(x(n−1:n) , x(n−1:n) , n, µ, σ, r)] = a + E[log v(x(n−1:n) , x(n−1:n) ; n, µ − a, σ, r)]
41
where the signals in the RHS expectation have the same conditional distribution G|v as those
on the LHS, but the latent v now has a prior with mean µ − a on the RHS. Now take a = αzj
for any observation j. Then by specification µ − a = 0, and
E[log p(n, zj , α, β, r)] = αzj + E[log p(n, zj , 0, σ, r)]
The variance result follows in similar fashion.
G. Proof of Proposition 5
To begin, one must establish the results on the moments. (b) is immediate, since by Proposition
4, Ω[log p|n, z, m, θ] does not depend on µ, and by assumption ξ enters only µ and not σ and
r. For (a), I argue as in Pinkse (2000) and write:
E[log p|n, z, m, θ] = αz + E[log p|n, z, α = 0, β, r] + E[ξ|I, z 0 , m]
= αz + E[log p|n, z, α = 0, β, r] + E[ξ|m]
= αz + E[log p|n, z, α = 0, β, r] + h−1 (m)
= αz + E[log p|n, z, α = 0, β, r] + f (m)
where the first line follows by Proposition 2 above. The third line follows on noting that
I − m = g(z 0 , W ) is independent of ξ, as is z 0 . The existence of an inverse in the fourth line
follows by the monotonicity of h.
H. Asymptotics for the Control Function Estimator
In this section I provide a discussion of the requirements for consistency and asymptotic normality of the PML estimator with a control function. All the analysis here is based on Andrews
(1994a) and Andrews (1994b). Define the sample and limiting objective functions:
J X
(log pj − E[log p|n, zj , mj , θ])2
LJ (θ, m) = (−1/2J)
log(Ω[log p|n, zj , θ]) +
Ω[log p|n, zj , θ]
j=1
(log p − E[log p|n, z, m, θ])2
L∞ (θ, m) = (−1/2)E log(Ω[log p|n, z, θ]) +
Ω[log p|n, z, θ]
Denote the true parameter vector as θ0 and the true residual as m0 . Following Theorem
A-1 in Andrews (1994a), four requirements need to be satisfied for consistency. The first is
that LJ (θ, m) uniformly weakly converges to L∞ (θ, m) on Θ × F, for F a function space for
42
m = I − E[I|W, z 0 ]. This follows by a WLLN since the sample consists of independent draws
from the stochastic process that generates the random variables (P, Z, N, W ). The second
is that the supremum distance supθ∈Θ ||L∞ (θ, m)
b − L∞ (θ, m0 )|| converges in probability to
zero. This follows from the consistency of the first stage kernel estimator for m0 . Thirdly,
I need uniform continuity of LJ (θ, m), which is straightforward. Finally, I need a separation
condition, so that for every neighborhood Θ0 of θ0 , inf θ∈Θ/Θ0 L∞ (θ, m0 ) > L∞ (θ0 , m0 ). This
follows from identification of the model and the Kulback inequality, as in Gourieroux, Monfort,
and Trognon (1984).
Obtaining asymptotic normality is somewhat less straightforward. The idea is to first show
√
that T (θbm − θ0 ) is asymptotically normally distributed, where θbm is the maximizer of the
0
0
sample criterion function with the true residuals m0 substituted for the estimated residuals m.
b
√
Then if the convergence of m
b to m0 is sufficiently smooth, asymptotic normality of T (θb −
θ) will follow. The formal requirements are given in Theorem 1 of Andrews (1994a). The
√
asymptotic normality of T (θbm0 − θ0 ) follows immediately from the asymptotic normality
results in Gourieroux, Monfort, and Trognon (1984), under standard conditions on LJ (θ, m).
Here we will also need to extend these standard conditions to all of F so that LJ (θ, m) is twice
continuously differentiable and the vector of first order conditions satisfy uniform WLLNS for
all m ∈ F. But the key requirements are an asymptotic orthogonality condition on the vector
√
of first order conditions T ∂/∂θ(LJ (θ0 , m)),
b
and the stochastic equicontinuity of LJ around
m0 . For a kernel-based estimator, Andrews (1994b) provides sufficient conditions on the first
stage estimator for these to hold. For the asymptotic orthogonality condition, it is necessary
that the kernel estimator be adaptive. I implement the kernel estimator with bandwidth chosen
by cross-validation to satisfy this. For the stochastic equicontinuity condition, it is necessary
to use kernels with smooth derivatives, and trim observations in a smooth manner. To satisfy
these conditions, I use a multivariate Gaussian kernel, and underweight outlying observations
when forming the conditional expectation m.
b It is important that the trimming function
has the property not only of assigning zero weight to outlying observations, but that it also
underweights observations near to the outliers, and so as suggested in Andrews (1994b) I use a
second kernel to re-weight observations based on their mahalanobis distance from other points
in the data.
I. Demand System Computation
In this section I provide a number of additional details on the demand system computation. I
do this for the case in which a control function is not used, as the case with a control function
is extremely similar apart from the first stage estimation of residuals. The first step is to
43
compute the moments E[log p|n, µ = 0, σ, r] and Ω[log p|n, µ = 0, σ, r] for a grid of values of r,
σ and n (my grid has 3600 points). To do this, I use the following formulae:
R q
e φ((x − q)/r)2 Φ((x − q)/r)n−1 φ((q − µ)/σ)dq
v(x, x, n; µ, σ, r) = R
φ((x − q)/r)2 Φ((x − q)/r)n−1 φ((q − µ)/σ)dq
Z Z
E[log p|n, µ = 0, σ, r] =
log v(x, x, n, µ = 0, σ, r)φ((x − q)/r) (1 − Φ((x − q)/r)) Φ((x − q)/r)n−2 φ(q/σ)dxdq
Z Z
E[(log p)2 |n, µ = 0, σ, r] =
log v(x, x, n, µ = 0, σ, r)2 φ((x − q)/r) (1 − Φ((x − q)/r)) Φ((x − q)/r)n−2 φ(q/σ)dxdq
where q = log v is the latent log value of the object, and φ and Φ are the standard normal density and cumulative distribution function respectively. I compute these moments
to very high accuracy using Gauss-Kronrod quadrature. In the algorithm below, when required to provide either of these moments for a point not on the grid, I use three dimensional linear interpolation, which remains highly accurate. I transform the indices βz and
rIN DEX with the functions κ(βz) = σ + (σ − σ) (0.5 + arctan(βz/π)), and ν(rIN DEX ) =
r + (r − r) (0.5 + arctan(rIN DEX /π)) where the grid boundaries for fixed n are [σ, σ] and [r, r].
These transformations constrain the indices to lie on the grid, which is convenient for computation. The estimated values do not lie near the boundaries, so my grid boundary choice does
not appear to apply constraints to the estimator.
The algorithm for finding the estimate θb given this grid of pre-computed values is then as
follows:
1. Draw an initial parameter vector (β0 , r0 ). For each observation, generate σj under
the specification and then interpolate on the grid to find E[log p|n, µ = 0, σj , r] and
Ω[log p|n, µ = 0, σj , r].
2. As in the text, generate a temporary dependent variable yj = log pj − E[log p|n, µ =
0, σj , r] and weights 1/Ω[log p|n, µ = 0, σj , r], and find α
b(β, r) by WLS.
3. Evaluate the objective function, and using a quasi-Newton algorithm, pick a new point
(β1 , r1 ). Repeat until convergence has been achieved.
J. Additional Simulation Details
There are two steps to the simulation: estimating the counterfactual prior parameters µc and
σ c , and computation of the expected true, counterfactual and baseline prices. For the first step,
note that µcj = E[˜
v |zj0 ] = E[E[˜
v |Ij , zj0 ]|zj0 ] = E[µj |zj0 ] = α0 zj0 + αI E[I|zj0 ]. I replace the parameter α with the structural estimate α
b, and the term E[I|zj0 ] with a nonparametric kernel estimate
r
c
c
Ib to get an estimate of µj . Similar analysis shows σj = E[σj2 |zj0 ] + αI2 E[I 2 |zj0 ] − E[I|zj0 ]2 . I
44
estimate all unknown terms nonparametrically. Then I use the following formulas in computing
the true, counterfactual and baseline expected prices:
E[pj |I, z 0 ] =
Z Z
E[pcj |I, z 0 ]
Z Z
=
E[pbj |z 0 ] =
Z Z
v(x, x, n, µ
cj , σbj , rb)φ((x − q)/b
r) (1 − Φ((x − q)/b
r)) Φ((x − q)/b
r)n−2 φ((q − µ
cj )/σbj )dxdq
cjc , rb)φ((x − q)/b
ccj , σ
r) (1 − Φ((x − q)/b
r)) Φ((x − q)/b
r)n−2 φ((q − µ
cj )/σbj )dxdq
v(x, x, n, µ
cjc )dxdq
ccj )/σ
cjc , rb)φ((x − q)/b
ccj , σ
r) (1 − Φ((x − q)/b
r)) Φ((x − q)/b
r)n−2 φ((q − µ
v(x, x, n, µ
where the dependence on I and z of µ and σ is suppressed. I compute the integrals using
Gauss-Kronrod quadrature, evaluating all three for a sample of 2000 points from my data set.
K. Testing for Common Values
I justified the use of a symmetric common values (CV) auction model by arguing that the
common uncertainty generated by the information asymmetries between the seller and the
bidders is more important than idiosyncrasies in individual preferences. Here I provide a
formal test of symmetric common values against the alternative of symmetric private values
(PV). This test, originally proposed by Athey and Haile (2002), depends on the following
equality:
2
n−2
P r(B (n−2:n) < b) +
P r(B (n−1:n) < b) = P r(B (n−2:n−1) < b)
n
n
(9)
where B (i:n) denotes the i-th ordered bid in the n person auction.
This relationship holds in symmetric PV models since in those frameworks the number of
bidders n has no effect on valuations. By contrast, in CV models the Winner’s Curse effect
means that bids are on average lower as n increases than in the PV model. This implies that
the distribution on the LHS of (9) is first order stochastically dominated by that on the right
hand side.
I observe the second and third highest bids in every auction B (n−1:n) and B (n−2:n) , and thus for
each n > 2 can construct the distributions on either side of (9). Let Gn (b) = n2 P r(B (n−2:n) <
b) +
n−2
(n−1:n)
n P r(B
< b) and Hn (b) = P r(B (n−2:n−1) < b). To test for stochastic dominance,
I use a version of the Kolmogorov-Smirnov test statistic proposed by Haile, Hong, and Shum
(2003), given by:
δT =
n
¯
X
n=n
n
o
b Tn (ε) − H
b nT (ε)
sup G
(10)
ε
where n
¯ and n are respectively the highest and lower number of bidders observed in all auctions,
Pn¯
and T =
n=n Tn for Tn the number of observations of auctions with number of bidders
45
b Tn (ε) and H
b nT (ε) are calculated for each n from the empirical distribution function of
n. G
the observed residuals, Fbn (), where the residuals have been obtained from separate OLS
regressions of the second and third highest bids on covariates z. I use residuals instead of
the bids in forming the test statistic because the objects being auctioned are not identical,
and a sensible null hypothesis is that of conditionally independent private values, where the
distribution of values is identical across auctions conditional on the covariates z.
Under the null hypothesis, the distributions Gn and Hn are equal for each n, whilst under
the common values alternative, first order stochastic dominance implies that ST will be large.
To obtain an asymptotically valid critical value, I use a subsampling approach as in Haile,
Hong, and Shum (2003) and Linton, Maasoumi, and Whang (2005). Define the normalized
√
test statistic ST = T δT . This differs from Haile, Hong, and Shum (2003) because they are
obliged to use a nonparametric first stage in estimating the underlying valuations, and thus
obtain a slower uniform convergence rate. I draw m samples r1 · · · rm of size b from the original
dataset without replacement, calculating Sb for each one. Forming the empirical distribution
function Ψ of the m statistics Sb , I take the critical value for a test of size α to be the (1−α)-th
quantile, S1−α of Ψ. The validity of this approach follows from results in Politis, Romano, and
Wolf (1999). In practice, I choose the number of draws m to be 1000, and since results can be
sensitive to the choice of sample size, I consider two sample sizes, sizes 30% and 40% of my
original dataset. The results follow in Table 2 below:
Table 2: Test for Common Values
Critical Values
Sample Size
30 %
40 %
Test Statistic
S0.9
48.592
49.41
S0.95
50.184
50.393
51.664
S0.99
52.595
53.07
The test statistic is significant at the 5% level, and I can reject the null of symmetric private
values. But there is reason to view this result with caution, as in general this test will tend to
over-reject the null in an eBay context. This is because the third highest observed bid, b(n−2:n) ,
may not actually be the bid of the bidder with the third highest valuation (in a PV context)
or signal (in a CV context). As noted earlier, such a bidder may be too late in entering his
b Tn (b) may
or her bid, and not have it recorded. It follows that the estimated distribution G
be stochastically dominated by the true distribution Gn (b) even in a private values context,
where “true” should be interpreted here to mean the distribution of bids in the counterfactual
case that all bids were recorded. Nonetheless this result is consistent with the assumption of
symmetric common values in the model used in the body of the paper.
46
Table 3: Structural Demand Estimation
µ
Age
Age Squared
Log of Miles
Log of Text Size
Number of Photos
Manual Transmission
(1)
(2)
(3)
(4)
(5)
-0.2107
(0.0023)
0.0043
(0.0001)
-0.1258
(0.0059)
0.0537
(0.0065)
0.0185
(0.0009)
0.0404
(0.0111)
-0.2094
(0.0023)
0.0043
(0.0001)
-0.1248
(0.0058)
0.0471
(0.0065)
0.0179
(0.0009)
0.0404
(0.0111)
0.1915
(0.0159)
-0.2091
(0.0023)
0.0043
(0.0001)
-0.1246
(0.0058)
0.0592
(0.0068)
0.0179
(0.0009)
0.0385
(0.0110)
0.1897
(0.0159)
-0.0195
(0.0029)
-0.0027
(0.0013)
-0.2088
(0.0023)
0.0043
(0.0001)
-0.1242
(0.0058)
0.0610
(0.0070)
0.0176
(0.0009)
0.0378
(0.0110)
0.1925
(0.0160)
-0.0178
(0.0029)
-0.0025
(0.0013)
-0.0040
(0.0011)
0.0605
(0.0106)
-0.0361
(0.0154)
10.6771
(0.0764)
10.6952
(0.0759)
10.6726
(0.0759)
10.6485
(0.0767)
-0.2095
(0.0024)
0.0043
(0.0001)
-0.1256
(0.0060)
0.0785
(0.0079)
0.0207
(0.0010)
0.0341
(0.0110)
0.1983
(0.0159)
-0.0167
(0.0029)
-0.0027
(0.0013)
-0.0044
(0.0011)
0.0641
(0.0105)
-0.0352
(0.0154)
0.4761
(0.1175)
-0.0503
(0.0182)
-0.0139
(0.0022)
0.4388
(0.0937)
-0.0433
(0.0142)
-0.0052
(0.0018)
10.4939
(0.0853)
Featured Listing
Log Feedback
Percentage Negative Feedback
Total Number of Listings
Phone Number Provided
Address Provided
Warranty
Warranty*Logtext
Warranty*Photos
Inspection
Inspection*Logtext
Inspection*Photos
Constant
Estimated standard errors are given in parentheses. The table gives the estimated relationship between the
prior mean valuation µ and auction covariates. The nested specifications (2)-(4) include controls for marketing
effects, seller feedback and dealer status. Specification (5) includes warranty and inspection dummies and their
interactions with the information measures, showing that the value of photos and text is lower when the car has
been inspected or is under warranty.
47
Table 3: Structural Demand Estimation (continued)
σ
Age
Log of Text Size
Photos
Constant
rIN DEX
Marginal Effects for σ
Age
Log of Text Size
Photos
Mean σ
r
(1)
(2)
(3)
(4)
(5)
0.0336
(0.0022)
-0.0185
(0.0357)
-0.0178
(0.0053)
-1.1490
(0.2234)
-0.0630
(0.0373)
0.0337
(0.0022)
-0.0206
(0.0360)
-0.0182
(0.0054)
-1.1384
(0.2241)
-0.0648
(0.0364)
0.0337
(0.0022)
-0.0215
(0.0360)
-0.0182
(0.0054)
-1.1344
(0.2239)
-0.0637
(0.0366)
0.0335
(0.0022)
-0.0221
(0.0360)
-0.0182
(0.0054)
-1.1287
(0.2237)
-0.0619
(0.0374)
0.0335
(0.0022)
-0.0220
(0.0363)
-0.0183
(0.0055)
-1.1345
(0.2254)
-0.0642
(0.0363)
0.0127
-0.0070
-0.0067
0.8472
1.2099
0.0126
-0.0077
-0.0068
0.8448
1.2088
0.0126
-0.0081
-0.0068
0.8442
1.2095
0.0125
-0.0083
-0.0068
0.8433
1.2106
0.0124
-0.0082
-0.0068
0.8402
1.2092
Estimated standard errors are given in parentheses. The parameters in this table show the estimated relationship
between the prior standard deviation σ, which is a measure of prior uncertainty, and auction covariates z. Since
the relationship between σ and z is modeled as being non-linear, the marginal effects are easiest to interpret.
An estimate of r, the standard deviation of bidders private signals, is also provided.
48
Table 4: Structural Demand Estimation by Car Group
µ
Age
Age Squared
Log of Miles
Log of Text Size
Photos
Manual Transmission
Constant
σ
Age
Log of Text Size
Photos
Constant
rIN DEX
Marginal Effects for σ
Age
Log of Text Size
Photos
Mean σ
r
Classic Cars
Reliable Cars
Pickups
-0.1794
(0.0029)
0.0038
(0.0001)
-0.1370
(0.0070)
0.0657
(0.0095)
0.0202
(0.0011)
0.2204
(0.0140)
10.8249
(0.0953)
-0.1732
(0.0159)
0.0007
(0.0006)
-0.1059
(0.0213)
0.0329
(0.0206)
0.0062
(0.0024)
0.0881
(0.0221)
10.7823
(0.2557)
-0.1936
(0.0038)
0.0030
(0.0001)
-0.1097
(0.0124)
0.0339
(0.0115)
0.0172
(0.0022)
-0.1757
(0.0231)
11.1512
(0.1646)
0.0278
(0.0026)
-0.0273
(0.0400)
-0.0132
(0.0050)
-1.1110
(0.2635)
-0.0793
(0.0292)
0.0950
(0.0306)
-0.0236
(0.1542)
-0.0169
(0.0192)
-2.0891
(1.0739)
-0.2537
(0.0290)
0.0321
(0.0035)
-0.0062
(0.0853)
-0.0213
(0.0156)
-1.1467
(0.5371)
0.0248
(0.5906)
0.0109
-0.0107
-0.0052
0.8512
1.1996
0.0190
-0.0047
-0.0034
0.6567
1.0918
0.0109
-0.0021
-0.0072
0.8065
1.2658
Estimated standard errors are given in parentheses. This table gives the estimated relationship between the
structural parameters and the covariates for each of the main car groups in my dataset. In all cases the prior
mean is positively related to the amount of text and photos, but the magnitudes vary significantly by group.
49
Table 5: Structural Demand Estimation with Controls
No Control
µ
Age
Age Squared
Log of Miles
Log of Text Size
Manual Transmission
Control
Control Squared
Constant
σ
Age
Log of Text Size
Constant
rIN DEX
Marginal Effects for σ
Age
Log of Text Size
Mean σ
r
Control
Control
Control
(h = 0.2)
(h = 0.1)
(h = 0.3)
OLS Control
-0.2037
(0.0037)
0.0043
(0.0001)
-0.1218
(0.0085)
0.0623
(0.0082)
0.0565
(0.0170)
-0.2975
(0.0496)
0.6089
(0.0418)
10.6941
(0.1152)
-0.2041
(0.0037)
0.0044
(0.0001)
-0.1221
(0.0084)
0.0444
(0.0104)
0.0575
(0.0170)
0.0508
(0.0177)
-0.0179
(0.0116)
10.8380
(0.1234)
-0.2040
(0.0037)
0.0043
(0.0001)
-0.1222
(0.0084)
0.0486
(0.0097)
0.0575
(0.0170)
0.0440
(0.0161)
-0.0175
(0.0116)
10.8074
(0.1209)
-0.2041
(0.0037)
0.0044
(0.0001)
-0.1221
(0.0084)
0.0406
(0.0112)
0.0574
(0.0170)
0.0556
(0.0190)
-0.0180
(0.0116)
10.8657
(0.1266)
-0.2040
(0.0037)
0.0043
(0.0001)
-0.1184
(0.0085)
0.0466
(0.0089)
0.0579
(0.0169)
0.0779
(0.0163)
-0.0182
(0.0114)
10.7643
(0.1156)
0.0317
(0.0035)
-0.1256
(0.0485)
-0.6006
(0.4186)
-0.0532
(0.0495)
0.0316
(0.0035)
-0.1248
(0.0483)
-0.6072
(0.4176)
-0.0534
(0.0493)
0.0316
(0.0035)
-0.1245
(0.0483)
-0.6093
(0.4177)
-0.0535
(0.0492)
0.0316
(0.0035)
-0.1250
(0.0483)
-0.6055
(0.4174)
-0.0534
(0.0493)
0.0316
(0.0035)
-0.1247
(0.0484)
-0.6103
(0.4182)
-0.0541
(0.0487)
0.0113
-0.0450
0.8324
1.2162
0.0113
-0.0447
0.8319
1.2160
0.0113
-0.0446
0.8319
1.2160
0.0113
-0.0448
0.8319
1.2160
0.0113
-0.0445
0.8311
1.2156
Estimated standard errors are given in parentheses. I do not account for first stage estimation error in computing
the errors. The different specifications provide estimates with and without the use of a control function, and
for varying bandwidth h in the nonparametric first stage. The final specification is estimated with an OLS first
stage.
50
Table 6: Demand Estimation by Car Group with Control
µ
Age
Age Squared
Log of Miles
Log of Text Size
Manual Transmission
Control
Control Squared
Constant
σ
Age
Log of Text Size
Constant
rIN DEX
Marginal Effects for σ
Age
Log of Text Size
Mean σ
r
Classic Cars
Reliable Cars
Pickups
-0.1629
(0.0044)
0.0036
(0.0001)
-0.1341
(0.0097)
0.0660
(0.0192)
0.2499
(0.0223)
0.0749
(0.0305)
-0.0293
(0.0167)
10.9973
(0.1732)
-0.1815
(0.0253)
0.0013
(0.0010)
-0.0804
(0.0331)
-0.0216
(0.0428)
0.0570
(0.0303)
0.1157
(0.0370)
-0.0180
(0.0201)
10.8878
(0.5546)
-0.1925
(0.0058)
0.0031
(0.0002)
-0.1028
(0.0163)
0.0108
(0.0153)
-0.1607
(0.0334)
0.0641
(0.0319)
-0.0003
(0.0224)
11.3938
(0.2632)
0.0240
(0.0035)
-0.0766
(0.0529)
-0.8223
(0.4113)
-0.0407
(0.0550)
0.0760
(0.0599)
-0.2602
(0.2543)
-0.4439
(2.4866)
-0.0190
(0.5599)
0.0331
(0.0048)
-0.1750
(0.0915)
-0.1309
(0.7419)
0.1491
(0.8446)
0.0101
-0.0322
0.8753
1.2241
0.0124
-0.0423
0.6064
1.2379
0.0104
-0.0548
0.7784
1.3442
Estimated standard errors are in parentheses. I do not account for first stage estimation error in computing
the errors. The three specifications show the estimated relationship between the structural parameters and the
covariates for different car groups. After including the control function, I find no significant relationship between
my information measures and the prior mean in the case of reliable cars and pickups.
51