1. science
2. mathematics
3. geometry

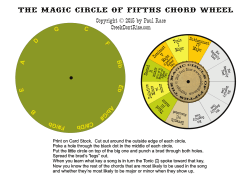
Chapter 11
Resource Masters
New York, New York
Columbus, Ohio
Woodland Hills, California
Peoria, Illinois
CONSUMABLE WORKBOOKS Many of the worksheets contained in the Chapter
Resource Masters booklets are available as consumable workbooks in both
English and Spanish.
Study Guide Workbook
Skills Practice Workbook
Practice Workbook
Spanish Study Guide and Assessment
0-07-869623-2
0-07-869312-8
0-07-869622-4
0-07-869624-0
ANSWERS FOR WORKBOOKS The answers for Chapter 11 of these workbooks
can be found in the back of this Chapter Resource Masters booklet.
StudentWorksTM This CD-ROM includes the entire Student Edition along with the
English workbooks listed above.
TeacherWorksTM All of the materials found in this booklet are included for viewing
and printing in the Geometry: Concepts and Applications TeacherWorks
CD-ROM.
Copyright © The McGraw-Hill Companies, Inc. All rights reserved.
Printed in the United States of America. Permission is granted to reproduce the
material contained herein on the condition that such material be reproduced only
for classroom use; be provided to students, teachers, and families without charge;
and be used solely in conjunction with Glencoe Geometry: Concepts and
Applications. Any other reproduction, for use or sale, is prohibited without prior
written permission of the publisher.
Send all inquiries to:
Glencoe/McGraw-Hill
8787 Orion Place
Columbus, OH 43240-4027
ISBN: 0-07-869277-6
1 2 3 4 5 6 7 8 9 10
Geometry: Concepts and Applications
Chapter 11 Resource Masters
024
11 10 09 08 07 06 05 04
Contents
Lesson 11-5
Study Guide and Intervention . . . . . . . . . . . . . . . 471
Skills Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . 472
Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 473
Reading to Learn Mathematics . . . . . . . . . . . . . . 474
Enrichment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 475
Vocabulary Builder . . . . . . . . . . . . . . . . . vii-viii
Proof Builder . . . . . . . . . . . . . . . . . . . . . . . . . ix
Lesson 11-1
Study Guide and Intervention . . . . . . . . . . . . . . . 451
Skills Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . 452
Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 453
Reading to Learn Mathematics . . . . . . . . . . . . . . 454
Enrichment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 455
Lesson 11-6
Study Guide and Intervention . . . . . . . . . . . . . . . 476
Skills Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . 477
Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 478
Reading to Learn Mathematics . . . . . . . . . . . . . . 479
Enrichment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 480
Lesson 11-2
Study Guide and Intervention . . . . . . . . . . . . . . . 456
Skills Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . 457
Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 458
Reading to Learn Mathematics . . . . . . . . . . . . . . 459
Enrichment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 460
Chapter 11 Assessment
Chapter 11 Test, Form 1A. . . . . . . . . . . . . . . 481-482
Chapter 11 Test, Form 1B . . . . . . . . . . . . . . . 483-484
Chapter 11 Test, Form 2A. . . . . . . . . . . . . . . 485-486
Chapter 11 Test, Form 2B . . . . . . . . . . . . . . . 487-488
Chapter 11 Extended Response
Assessment. . . . . . . . . . . . . . . . . . . . . . . . . . . . 489
Chapter 11 Mid-Chapter Test . . . . . . . . . . . . . . . . 490
Chapter 11 Quizzes A & B. . . . . . . . . . . . . . . . . . 491
Chapter 11 Cumulative Review . . . . . . . . . . . . . . 492
Chapter 11 Standardized
Test Practice . . . . . . . . . . . . . . . . . . . . . . . 493-494
Lesson 11-3
Study Guide and Intervention . . . . . . . . . . . . . . . 461
Skills Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . 462
Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 463
Reading to Learn Mathematics . . . . . . . . . . . . . . 464
Enrichment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 465
Lesson 11-4
Study Guide and Intervention . . . . . . . . . . . . . . . 466
Skills Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . 467
Practice. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 468
Reading to Learn Mathematics . . . . . . . . . . . . . . 469
Enrichment . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 470
© Glencoe/McGraw-Hill
Standardized Test Practice
Student Recording Sheet . . . . . . . . . . . . . . . . . . A1
ANSWERS . . . . . . . . . . . . . . . . . . . . . . . . . . A2-A23
iii
Geometry: Concepts and Applications
A Teacher’s Guide to Using the
Chapter 11 Resource Masters
The Fast File Chapter Resource system allows you to conveniently file the
resources you use most often. The Chapter 11 Resource Masters include the core
materials needed for Chapter 11. These materials include worksheets, extensions,
and assessment options. The answers for these pages appear at the back of this
booklet.
All of the materials found in this booklet are included for viewing and printing in
the Geometry: Concepts and Applications TeacherWorks CD-ROM.
Vocabulary Builder Pages vii-viii include a
student study tool that presents the key
vocabulary terms from the chapter. Students are
to record definitions and/or examples for each
term. You may suggest that students highlight or
star the terms with which they are not familiar.
Skills Practice There is one master for each
lesson. These provide computational practice at
a basic level.
When to Use These worksheets can be used
with students who have weaker mathematics
backgrounds or need additional reinforcement.
When to Use Give these pages to students
before beginning Lesson 11-1. Encourage them
to add these pages to their Geometry: Concepts
and Applications Interactive Study Notebook.
Remind them to add definitions and examples as
they complete each lesson.
Practice There is one master for each lesson.
These problems more closely follow the
structure of the Practice section of the Student
Edition exercises. These exercises are of average
difficulty.
When to Use These provide additional
Proof Builder Page ix includes another
student study tool that presents theorems and
postulates from the chapter. Students are to write
each theorem or postulate in their own words,
including illustrations if they choose to do so.
You may suggest that students highlight or star
the theorems or postulates with which they are
not familiar.
When to Use Give this page to students
before beginning Lesson 11-1. Encourage them
to add this page to their Geometry: Concepts
and Applications Interactive Study Notebook.
Remind them to update it as they complete each
lesson.
practice options or may be used as homework
for second day teaching of the lesson.
Reading to Learn Mathematics One
master is included for each lesson. The first
section of each master presents key terms from
the lesson. The second section contains
questions that ask students to interpret the
context of and relationships among terms in the
lesson. Finally, students are asked to summarize
what they have learned using various
representation techniques.
When to Use This master can be used as a
study tool when presenting the lesson or as an
informal reading assessment after presenting the
lesson. It is also a helpful tool for ELL (English
Language Learners) students.
Study Guide There is one Study Guide
master for each lesson.
When to Use Use these masters as reteaching
activities for students who need additional
reinforcement. These pages can also be used in
conjunction with the Student Edition as an
instructional tool for those students who have
been absent.
© Glencoe/McGraw-Hill
iv
Geometry: Concepts and Applications
Enrichment There is one master for each
lesson. These activities may extend the concepts
in the lesson, offer a historical or multicultural
look at the concepts, or widen students’
perspectives on the mathematics they are
learning. These are not written exclusively for
honors students, but are accessible for use with
all levels of students.
Intermediate Assessment
• A Mid-Chapter Test provides an option to
assess the first half of the chapter. It is
composed of free-response questions.
• Two free-response quizzes are included to
offer assessment at appropriate intervals in
the chapter.
When to Use These may be used as extra
credit, short-term projects, or as activities for
days when class periods are shortened.
Continuing Assessment
Assessment Options
• The Cumulative Review provides students
an opportunity to reinforce and retain skills
as they proceed through their study of
geometry. It can also be used as a test. The
master includes free-response questions.
The assessment section of the Chapter 11
Resources Masters offers a wide range of
assessment tools for intermediate and final
assessment. The following lists describe each
assessment master and its intended use.
• The Standardized Test Practice offers
continuing review of geometry concepts in
multiple choice format.
Chapter Assessments
Chapter Tests
Answers
• Forms 1A and 1B contain multiple-choice
questions and are intended for use with
average-level and basic-level students,
respectively. These tests are similar in
format to offer comparable testing
situations.
• Page A1 is an answer sheet for the
Standardized Test Practice questions that
appear in the Student Edition on page 493.
This improves students’ familiarity with the
answer formats they may encounter in test
taking.
• Forms 2A and 2B are composed of freeresponse questions aimed at the averagelevel and basic-level student, respectively.
These tests are similar in format to offer
comparable testing situations.
• The answers for the lesson-by-lesson
masters are provided as reduced pages with
answers appearing in red.
• Full-size answer keys are provided for the
assessment options in this booklet.
All of the above tests include a challenging
Bonus question.
• The Extended Response Assessment
includes performance assessment tasks that
are suitable for all students. A scoring rubric
is included for evaluation guidelines.
Sample answers are provided for
assessment.
© Glencoe/McGraw-Hill
v
Geometry: Concepts and Applications
Chapter 11 Leveled Worksheets
Glencoe’s leveled worksheets are helpful for meeting the needs of every
student in a variety of ways. These worksheets, many of which are found in
the FAST FILE Chapter Resource Masters, are shown in the chart below.
• The Prerequisite Skills Workbook provides extra practice on the basic
skills students need for success in geometry.
• Study Guide and Intervention masters provide worked-out examples as
well as practice problems.
• Reading to Learn Mathematics masters help students improve reading
skills by examining lesson concepts more closely.
• Noteables™: Interactive Study Notebook with Foldables™ helps
students improve note-taking and study skills.
• Skills Practice masters allow students who are progressing at a slower
pace to practice concepts using easier problems. Practice masters
provide average-level problems for students who are moving at a regular
pace.
• Each chapter’s Vocabulary Builder master provides students the
opportunity to write out key concepts and definitions in their own words.
The Proof Builder master provides students the opportunity to write the
chapter’s postulates and theorems in their own words.
• Enrichment masters offer students the opportunity to extend their
learning.
Ten Different Options to Meet the Needs of
Every Student in a Variety of Ways
primarily skills
primarily concepts
primarily applications
BASIC
AVERAGE
1
Prerequisite Skills Workbook
2
Study Guide and Intervention
3
Reading to Learn Mathematics
4
NoteablesTM: Interactive Study Notebook with FoldablesTM
5
Skills Practice
6
Vocabulary Builder
7
Proof Builder
8
Parent and Student Study Guide (online)
© Glencoe/McGraw-Hill
9
Practice
10
Enrichment
vi
ADVANCED
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Reading to Learn Mathematics
Vocabulary Builder
This is an alphabetical list of the key vocabulary terms you will learn in Chapter 11.
As you study the chapter, complete each term’s definition or description.
Remember to add the page number where you found the term.
Vocabulary Term
Found
on Page
Definition/Description/Example
adjacent arcs
arcs
center
central angle
chord
circle
circumference
sir•KUM•fur•ents
circumscribed
concentric
diameter
(continued on the next page)
© Glencoe/McGraw-Hill
vii
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Reading to Learn Mathematics
Vocabulary Builder (continued)
Vocabulary Term
Found
on Page
Definition/Description/Example
experimental probability
ek•speer•uh•MEN•tul
inscribed
loci
locus
major arc
minor arc
pi ()
radius
RAY•dee•us
sector
semicircle
theoretical probability
thee•uh•RET•i•kul
© Glencoe/McGraw-Hill
viii
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Reading to Learn Mathematics
Proof Builder
This is a list of key theorems and postulates that you will learn in Chapter 11. As you
study the chapter, write each theorem or postulate in your own words. Include
illustrations as appropriate. Remember to include the page number where you
found the postulate.
Theorem or Postulate
Found
on Page
Definition/Description/Example
Theorem 11-1
Theorem 11-2
Theorem 11-3
Theorem 11-4
Theorem 11-5
Theorem 11-6
Theorem 11-7
Circumference of a Circle
Theorem 11-8
Area of a Circle
Theorem 11-9
Area of a Sector of a Circle
Postulate 11-1
Arc Addition Postulate
© Glencoe/McGraw-Hill
ix
Geometry: Concepts and Applications
BLANK
11–1
NAME
DATE
PERIOD
Study Guide
Parts of a Circle
A circle is the set of all points in a plane that are a given
distance from a given point in the plane called the center.
Various parts of a circle are labeled in the figure at the right.
Note that the diameter is twice the radius.
Example:
is a diameter.
In F, AC
• Name the circle. F

• Name a radius. AF , C
F
, or BF
• Name a chord that is not a diameter.
BC
Use S to name each of the following.
1. the center S
  
2. three radii SR, SM, ST
3. a diameter R
T
4. a chord X
Y or R
T
Use P to determine whether each
statement is true or false.
is a radius of P. true
5. PC
6. AC
is a chord of P. true
7. If PB = 7, then AC = 14.
true
8-9. See students’ work.
On a separate sheet of paper, use a compass and a
ruler to make a drawing that fits each description.
is a diameter.
8. A has a radius of 2 inches. QR
is 1 inch long.
9. G has a diameter of 2 inches. Chord BC
© Glencoe/McGraw-Hill
451
Geometry: Concepts and Applications
NAME
11–1
DATE
PERIOD
Skills Practice
Parts of a Circle
Use A at the right to determine whether each statement is true or false.
is a radius of A. true
1. AT
S
2. R
B
is a chord of A. false
3. ZU 2(ZA)
R
Z
B
true
T
C
A
4. SA SW false
5. AT BX
Y
U
false
X W
6. SW
is a diameter of A. true
7. SW
is a chord of A. true
8. AT AZ true
9. AT
is a chord of A. false
10. SU RX false
11. SA AU true
12. S
Y
is a chord of A. true
13. SC SA false
14. Z
U
is a chord of A. true
15. Z
U
is a radius of A. false
16. B
U
is a chord of A. false
Circle W has a radius of 15 units, and Z has a radius of 10 units.
17. If XY 7, find YZ. 3
18. If XY 7, find WX. 8
T
19. If XY 7, find TX. 23
W
Z
X
Y
R
20. If XY 7, find WR. 28
© Glencoe/McGraw-Hill
452
Geometry: Concepts and Applications
NAME
11–1
DATE
PERIOD
Practice
Parts of a Circle
Refer to the figure at the right.
1. Name the center of P. P
2. Name three radii of the circle.
A
P
, PD
, PB
3. Name a diameter. A
B
4. Name two chords. A
D
, AB
Use circle P to determine whether each statement is true or false.
is a radius of circle P. true
5. PB
6. AB
is a radius of circle P. false
7. CA 2(PE)
true
8. PB
is a chord of circle P. false
9. AB
is a chord of circle P.
true
10. A
B
is a diameter of circle P. false
11. A
C
is a diameter of circle P. true
12. PA PD
true
© Glencoe/McGraw-Hill
453
Geometry: Concepts and Applications
11–1
NAME
DATE
PERIOD
Reading to Learn Mathematics
Parts of a Circle
Key Terms
circle the set of all points in a plane that are a given distance
from a given point in the plane, called the center of the circle
radius (RAY•dee•us) a segment whose endpoints are the
center of the circle and a point on the circle
chord (CORD) a segment whose endpoints are on the circle
diameter a chord that contains the center of the circle
concentric circles that lie in the same plane, have the same
center, and have radii of different lengths
Reading the Lesson
1. Tell whether each statement is always, sometimes, or never true. If the statement
is not always true, explain why.
a. The measure of the diamenter of a circle is one-half the measure of the radius
of the circle. Never; the measure of the diameter of a circle is twice
the measure of the radius of the circle.
b. If you draw any two circles, they are similar. always
c. A diameter of a circle is a chord. always
d. A chord of a circle is a diameter. Sometimes; if the chord contains the
center, then it is a diameter.
2. Match each description from the first column with the best term from the second
column. One term is used more than once.
a. a segment whose endpoints are on a circle iii
i.
b. the set of all points in a plane that are the same distance
from a given point iv
ii. diameter
c. a chord that passes through the center of a circle ii
iii. chord
d. a segment whose endpoints are the center and any point
on a circle i
iv. circle
radius
Helping You Remember
3. A good way to remember a new geometric term is to relate the word or its parts
to geometric terms you already know. Look up the origins of the two parts of the
word diameter in a dictionary. Explain the meaning of each part and give a term
you already know that shares the origin of that part. Sample answer: The
first part comes from dia, which means across or through, as in
diagonal. The second part comes from metron, which means
measure, as in geometry.
© Glencoe/McGraw-Hill
454
Geometry: Concepts and Applications
11–1
NAME
DATE
PERIOD
Enrichment
Constructing Designs
Many designs can be made using geometric constructions. Two
examples are stained glass rose windows found in churches and
Pennsylvania Dutch hex designs found on barns.
Use your compass to
draw a circle.
Then, without changing
the compass setting,
move the point to a point
on the circle. Draw a
second circle.
Place the point on one
of the points where the
two circles intersect.
Draw a circle. Repeat
five more times.
Use your compass and a straightedge to make a design like
the one below. (HINT: See the design above.) Check students’ drawings.
© Glencoe/McGraw-Hill
455
Geometry: Concepts and Applications
11–2
NAME
DATE
PERIOD
Study Guide
Arcs and Central Angles
An angle whose vertex is at the center of a circle is
called a central angle. A central angle separates a
circle into two arcs called a major arc and a minor
arc. In the circle at the right, CEF is a central
angle. Points C and F and all points of the circle
interior to CEF form a minor arc called arc CF.
. Points C and F and all points of the
This is written CF
circle exterior to CEF form a major arc called CGF .
You can use central angles to find the degree measure
of an arc. The arcs determined by a diameter are
called semicircles and have measures of 180.
AC
is
Examples: In R, m ARB 42 and a diameter.
.
1 Find mAB
Since ARB is a central angle and
m ARB 42, then mAB 42.
.
2 Find mACB
mACB 360 m ARB 360 42 or 318
.
3 Find mCAB
mCAB mABC mAB
180 42
222
M
T are diameters
Refer to P for Exercises 1–4. If S
N
and with m SPT 51 and m NPR 29, determine whether each
arc is a minor arc, a major arc, or a semicircle. Then find the
degree measure of each arc.
minor; 51
2. mST
1. mNR minor; 29
major; 260
3. mTSR
© Glencoe/McGraw-Hill
semicircle; 180
4. mMST
456
Geometry: Concepts and Applications
11–2
NAME
DATE
PERIOD
Skills Practice
Arcs and Central Angles
Find each measure in C if mACB 80, mAF 45, and AE
and F
D
are diameters.
1. mACF 45
2. mAB 80
3. mFCE 135
4. mEF 135
5. mABE 180
6. mBCE 100
7. mAFE 180
8. mDCE
9. mDE 45
11. mBAE 260
B
D
A
E
C
45
F
10. mBCD 55
12. mABF 315
In A, BD
is a diameter, mBAE 85, and mCAD 120. Determine whether each
statement is true or false.
13. mBAC 60 true
14. mCD mCAD true
C
15. ABE is a central angle. false
16. mBAC mDAE false
B
17. mCED 220 false
A
18. mBCD 180 true
D
E
19. mCE 145 true
20. mDAE mDE true
Q is the center of two circles with radii Q
D and Q
E. If mAQE 90 and mRE 115,
find each measure.
21. mAE 90
22. mRQE
115
23. mAR 155
24. mRQA
155
25. mAER 205
26. mBSD 270
27. mDS 115
28. mBD 90
© Glencoe/McGraw-Hill
R
S
B
Q
A
D
E
457
Geometry: Concepts and Applications
11–2
NAME
DATE
PERIOD
Practice
Arcs and Central Angles
In P, m1 140 and AC
is a diameter. Find each measure.
2. mBC 40
1. m2 40
3. mAB
140
4. mABC
180
In P, m2 m1, m2 4x 35, m1 9x 5, and
and A
C
are diameters. Find each of the following.
BD
5. x
6
8. m3
11. mEB
62
121
14. mCEB 242
6. mAE 59
7. mED 59
9. mAB 62
10. mEC 121
12. mCPB 118
13. mCB 118
15. mDC
16. mCEA 180
62
17. The table below shows how federal
funds were spent on education in 1990.
1990 Federal Funds
Spent for Education
1990 Federal Funds Spent for Education
Elementary/Secondary
Education for the Disabled
Post-Secondary Education
Public Library Services
Other
Total
$ 7,945,177
4,204,099
12,645,630
145,367
760,616
$25,700,889
a. Use the information to make a circle graph.
b. Out of the $12,645,630 spent on post-secondary education,
$10,801,185 went to post-secondary financial assistance. What
percent is that of the $12,645,630? 85.4%
© Glencoe/McGraw-Hill
458
Geometry: Concepts and Applications
11–2
NAME
DATE
PERIOD
Reading to Learn Mathematics
Arcs and Central Angles
Key Terms
central angle an angle whose vertex is the center of a circle
and whose sides intersect the circle
arc a set of points along a circle defined by a central angle
minor arc a part of the circle in the interior of a central angle
that measures less than 180
major arc a part of the circle in the exterior of a central angle
that measures greater than 180
semicircle an arc whose endpoints lie on a diameter of a circle
adjacent arcs arcs of a circle with one point in common
Reading the Lesson
1. Refer to P with diameter AC
. State whether each
statement is true or false. If the statement is false,
explain why.
a. DAB is a major arc. False; it is a minor arc because
B
A
52
P
C
D
its measure is less than 180.
b. ADC is a semicircle. true
c. AD CD true
d. BPC is an acute central angle. False; it is an obtuse central angle.
2. Refer to the figure in Exercise 1. Give each of the following arc measures. Explain
how you find the measure.
a. mAB The measure is 52 because the degree measure of a minor
arc is the degree measure of its central angle.
b. mBC The measure is 180 52, or 128, because ABC is a
semicircle and mAB mBC mABC.
c. mCD The measure is 90 because the degree measure of a minor
arc is the same as its central angle, which is a right angle.
d. mDAC The measure is 360 90, or 270, because the measure of a
major arc is 360 minus the degree measure of its central angle.
Helping You Remember
3. To help you remember terms in this lesson, sketch a circle. Label
and identify a minor arc, a major arc, and a semicircle.
Sample answer: In C with diameter X
Z
, XY is a
X
Y
C
minor arc, XZY is a major arc, and XYZ is a semicircle.
Z
© Glencoe/McGraw-Hill
459
Geometry: Concepts and Applications
11–2
NAME
DATE
PERIOD
Enrichment
Curves of Constant Width
A circle is called a curve of constant width because no matter how
you turn it, the greatest distance across it is always the same.
However, the circle is not the only figure with this property.
The figure at the right is called a Reuleaux triangle.
Q
P
1. Use a metric ruler to find the distance from P to
any point on the opposite side. 4.6 cm
2. Find the distance from Q to the opposite side.
4.6 cm
3. What is the distance from R to the opposite side?
4.6 cm
The Reuleaux triangle is made of three arcs. In the
example shown, PQ has center R, QR has center P, and
PR has center Q.
R
4. Trace the Reuleaux triangle above on a piece of paper and
cut it out. Make a square with sides the length you found in
Exercise 1. Show that you can turn the triangle inside the
square while keeping its sides in contact with the sides of
the square. See students’ work.
5. Make a different curve of constant width by starting with the
five points below and following the steps given.
Step 1: Place he point of your compass on
D with opening DA. Make an arc
with endpoints A and B.
B
A
Step 2: Make another arc from B to C that
has center E.
Step 3: Continue this process until you
have five arcs drawn.
C
E
D
Some countries use shapes like this for coins. They are useful
because they can be distinguished by touch, yet they will
work in vending machines because of their constant width.
6. Measure the width of the figure you made in Exercise 5.
Draw two parallel lines with the distance between them
equal to the width you found. On a piece of paper, trace the
five-sided figure and cut it out. Show that it will roll between
the lines drawn. 5.3 cm
© Glencoe/McGraw-Hill
460
Geometry: Concepts and Applications
11–3
NAME
DATE
PERIOD
Study Guide
Arcs and Chords
The following theorems state relationships between arcs,
chords, and diameters.
• In a circle or in congruent circles, two minor arcs are
congruent if and only if their corresponding chords are
congruent.
• In a circle, a diameter bisects a chord and its arc if and
only if it is perpendicular to the chord.
Example: In the circle, O is the center, OD 15, and
CD 24. Find x.
ED 1 CD
2
1
2
(24)
12
(OE)2 (ED)2 (OD)2
x2 122 152
x2 144 225
x2 81
x9
In each circle, O is the center. Find each measure.
2. KM
1. mNP
80
3. XY
24
32
4. Suppose a chord is 20 inches
long and is 24 inches from the
center of the circle. Find the
length of the radius. 26 in.
5. Suppose a chord of a circle
is 5 inches from the center
and is 24 inches long.
Find the length of the radius. 13 in.
6. Suppose the diameter of a circle is 30 centimeters long and a
chord is 24 centimeters long. Find the distance between the
chord and the center of the circle. 9 cm
© Glencoe/McGraw-Hill
461
Geometry: Concepts and Applications
11–3
NAME
DATE
PERIOD
Skills Practice
Arcs and Chords
Complete each sentence.
G
1. If SG RE, then S
E
R
?
2. If ST ET, then SMT 3. If TM
⊥
RG
, then RT 4. If ST TE, S
T
T
Q
E
T
R
B
A
?
6. If RE SG, then RME GMS
?
7. If RE
SG
, then RE ?
8. If TM
⊥
RG
, then ST ?
9. If TM
⊥
RG
, then S
Q
?
12. If SR AR, then R
G
⊥
G
M
B
A
SG
TE
Q
E
10. If T
M
⊥
RG
and ST TE, then SQT 11. If S
Q
, then T
M
⊥
EQ
E
S
TG
?
?
5. If RG
⊥
AS
, then S
B
EMT
?
EQT
?
G
R
?
A
S
?
Use B, where B
X
⊥W
Y
, to complete each sentence.
13. If BW 23, then BY ?
23
14. If WY 38, then WZ ?
19
15. If WZ 15, then WY ?
30
16. If BZ 6 and WZ 8, then WB 17. If WB 15 and BZ 9, then WZ 10
?
12
?
Z
X
Y
18. If WY 40 and BZ 15, then WB ?
25
19. If BY 30 and BZ 18, then WY ?
48
20. If mWY 110, then mWX 55
© Glencoe/McGraw-Hill
B
W
?
462
Geometry: Concepts and Applications
11–3
NAME
DATE
PERIOD
Practice
Arcs and Chords
In each figure, O is the center. Find each measure to the nearest
tenth.
1. YQ
2. mBC
12
72
3. Suppose a chord of a circle is 16 inches long and is 6 inches from
the center of the circle. Find the length of a radius. 10 in.
4. Find the length of a chord that is 5 inches from the center of a
circle with a radius of 13 inches. 24 in.
5. Suppose a radius of a circle is 17 units and a chord is 30 units
long. Find the distance from the center of the circle to the chord.
8 units
6. Find AB.
7. Find AB.
16
© Glencoe/McGraw-Hill
8
463
Geometry: Concepts and Applications
11–3
NAME
DATE
PERIOD
Reading to Learn Mathematics
Arcs and Chords
Reading the Lesson
1. Refer to Theorem 11-4. Write an if-then statement and its converse using this
theorem. In the same circle or congruent circles, if two chords are
congruent, then the two corresponding minor arcs are congruent.
In the same circle or congruent circles, if two minor arcs are
congruent, then their corresponding chords are congruent.
2. Refer to Theorem 11-5. Write an if-then statement and its converse using this
theorem. In a circle, if a diameter bisects a chord and its arc, then it
is perpendicular to the chord. In a circle, if a diameter is
perpendicular to a chord, then the diameter bisects the chord.
3. In P, the diameter measures 40 and
AC FD 24. Find the measures in each
exercise. Explain how you find each
measure.
B
A
C
G
P
D
H
a. PA PA is the length of the radius, which is
E
half of 40, or 20.
F
b. AG AG is half of AC, or 12, since the diameter is perpendicular to
the chord.
c. HE HE is PE PH. PE is the measure of a radius, which is half
of 40, or 20. So, HE 20 16, or 4.
d. FG FG is BF BG. is a diameter which measures 40. BG is the
BF
same as HE, or 4. So FG 40 4, or 36.
X
W
Helping You Remember
4. A good way to remember a mathematical concept
is to explain it in your own words. In the figure, C
contains quadrilateral WXYZ, where each vertex of
WXYZ lies on the circle. Explain why WXYZ is a square.
C
Z
Y
Sample answer: Since WCZ measures 90, all four angles measure
90. So, WXYZ is a rectangle. Since the angles are all congruent, the
minor arcs WX , XY, YZ , and WZ are all congruent. By Theorem 11-4,
if minor arcs are congruent, then their corresponding chords are
and WXYZ is a
XY
YZ
WZ
congruent. That means that WX
rhombus. Because WXYZ is both a rectangle and a rhombus, it is
a square.
© Glencoe/McGraw-Hill
464
Geometry: Concepts and Applications
NAME
11–3
DATE
PERIOD
Enrichment
Patterns from Chords
35
34
11
12 3
38 14
40
15
39
37
13
6
Some beautiful and interesting patterns result if you draw
chords to connect evenly spaced points on a circle. On the circle
shown below, 24 points have been marked to divide the circle
into 24 equal parts. Numbers from 1 to 48 have been placed
beside the points. Study the diagram to see exactly how this
was done.
10
16
41
17
9
42 1
2
8 3
8
43 19
44 2
7 31
6 30
0
5
21
23
4
48 2
27
1
25
6
2 2
47
28
3
46
29
4
22
45
33
1. Use your ruler and pencil to draw chords to connect
numbered points as follows: 1 to 2, 2 to 4, 3 to 6, 4 to 8, and
so on. Keep doubling until you have gone all the way around
the circle. What kind of pattern do you get? For figure, see
above. The pattern is a heart-shaped figure.
2. Copy the original circle, points, and numbers. Try other
patterns for connecting points. For example, you might try
tripling the first number to get the number for the second
endpoint of each chord. Keep special patterns for a possible
class display. See students’ work.
© Glencoe/McGraw-Hill
465
Geometry: Concepts and Applications
11–4
NAME
DATE
PERIOD
Study Guide
Inscribed Polygons
You can make many regular polygons by folding a circular piece
of paper. The vertices of the polygon will lie on the circle, so the
polygon is said to be inscribed in the circle.
1. Draw a circle with a radius of 2 inches and cut it out. Make the
following folds to form a square. See students’ work.
Step A
Fold the circle
in half.
Step B
Fold the circle
in half again.
Step C
Unfold the circle.
Step D
Fold the four
arcs designated
by the creases.
2. Draw another circle with a radius of 2 inches and cut it out.
Make the following folds to form a regular triangle.
See students’ work.
Step A
Fold one portion in
toward the center.
Step B
Fold another portion
in toward the center,
overlapping the first.
Step C
Fold the remaining third
of the circle in toward
the center.
For Exercises 3-5, see students’ work.
3. Cut out another circle and fold it to make a regular octagon.
Draw the steps used.
4. Cut out another circle and fold it to make a regular hexagon.
Draw the steps used.
5. Cut out a circle with radius 4 inches and fold it to make a
regular dodecagon. Draw the steps used.
© Glencoe/McGraw-Hill
466
Geometry: Concepts and Applications
11–4
NAME
DATE
PERIOD
Skills Practice
Inscribed Polygons
Use O to find x.
1. WM x 8, ZN 2x 5 3
WZ
2. WM 3x 10, ZN 2x 15 5
3. WM x 6, ZN 2x 12
P
6
O
Q
M
N
4. WM 2x 5, ZN x 5
10
5. WM 5x 1, ZN 2x 5
2
6. WM 4x 15, ZN 3x 19 4
7. WM x 8, ZN 2x 5
8. WM 4x, ZN 3x 1
3
1
9. WM x 1, ZN 2x 7
6
10. WM 20x 100, ZN 30x 80
2
Square SQUR is inscribed in C with a radius of 20 meters.
11. Find mSCQ. 90
S
A
Q
12. Find SQ to the nearest tenth. 28.3 m
C
13. Find CA to the nearest tenth. 14.2 m
© Glencoe/McGraw-Hill
467
R
U
Geometry: Concepts and Applications
11–4
NAME
DATE
PERIOD
Practice
Inscribed Polygons
Use a compass and straightedge to inscribe each polygon in a
circle. Explain each step. 1-2. See students’ work.
1. equilateral triangle
2. regular pentagon
Use circle O to find x.
x
x
3. AB 3x 5, CD 2x 1
6
4. AB 4x 2, CD 2x 6
2
5. AB 2x 1, CD 3x 4
5
6. AB 3(x 1), CD 2(x 5) 7
7. AB 3(x 1), CD 8x 13 2
8. AB 5(x 2), CD 10(x 1) 4
9. AB 3x 7, CD 4x 21
© Glencoe/McGraw-Hill
14
468
Geometry: Concepts and Applications
11–4
NAME
DATE
PERIOD
Reading to Learn Mathematics
Inscribed Polygons
Key Terms
inscribed polygon a polygon in which every vertex of the
polygon lies on the circle
Reading the Lesson
1. State whether each statement is true or false. If the statement is false,
explain why.
a. If every vertex of a polygon lies on the circle, then the polygon is a
circumscribed polygon. False; it is an inscribed polygon.
b. In a circle, two chords are congruent if they are equidistant from the center.
true
c. All regular polygons can be constructed by inscribing them in circles. False;
some regular polygons can be constructed by inscribing them in
circles.
d. If two chords are equidistant from the center of the circle, then the chords are
parallel. False; the chords are congruent.
e. If two vertices of a polygon lie on a circle, then the polygon is an inscribed
polygon. False; every vertex of the polygon must lie on the circle in
order for it to be inscribed.
2. Marian constructed a regular quadrilateral,
or square, by inscribing it in a circle, as
shown in the diagram at the right. Describe
the steps that she took to consruct the square.
Then explain why the figure is a square.
M
L
C
O
.
First, Marian drew the circle and the diameter LO
Next, she constructed the perpendicular bisector of
O
, extending the line to intersect C at points M
L
P
and P. Finally, she connected the consecutive
points in order to form square MOPL. The sides of the square are
chords of the circle. The four chords are congruent because they are
equidistant from the center of the circle.
Helping You Remember
3. Your friend has trouble remembering the difference between inscribed and
circumscribed polygons. What is an easy way to remember which is which?
Sample answer: The inscribed polygon is inside the circle, so the
circumscribed polygon must be outside the circle.
© Glencoe/McGraw-Hill
469
Geometry: Concepts and Applications
11–4
NAME
DATE
PERIOD
Enrichment
Area of Inscribed Polygons
A protractor can be used to inscribe a regular polygon in a circle.
Follow the steps below to inscribe a regular nonagon in N.
Step 1: Find the degree measure of each of
the nine congruent arcs. 40
Step 2: Draw 9 radii to form 9 angles with
the measure you found in Step 1.
The radii will intersect the circle in
9 points.
N
Step 3: Connect the nine points to form the
nonagon.
1. Find the length of one side of the
nonagon to the nearest tenth of a
centimeter. What is the perimeter of
the nonagon? 2.5 cm, P 22.5 cm
2. Measure the distance from the center perpendicular to one of
the sides of the nonagon. 3.3 cm
3. What is the area of one of the nine triangles formed? 4.125 cm2
4. What is the area of the nonagon? 37.125 cm2
Make the appropriate changes in Steps 1–3 above to inscribe
a regular pentagon in P. Answer each of the following.
5. Use a protractor to inscribe a regular
pentagon in P.
6. What is the measure of each of
the five congruent arcs? 72
7. What is the perimeter of the
pentagon to the nearest tenth
of a centimeter? 21 cm
P
8. What is the area of the pentagon
to the nearest tenth of a
centimeter? 30.45 cm2
© Glencoe/McGraw-Hill
470
Geometry: Concepts and Applications
11–5
NAME
DATE
PERIOD
Study Guide
Circumference of a Circle
distance
around a
circle
center
radius r
diameter d
circumference C
Examples: Find the circumference of each circle.
C d
C (6)
C 18.85
C 19 cm
C 2r
C 2(5)
C 10
C 31.4
C 31 m
Find the circumference of each circle.
1.
2.
C 44 ft
3.
C 50 in.
4. The radius is 6 1 feet. C 39 m
C 28 m
5. The diameter is 4.7 yards. C 15 yd
5
Solve. Round to the nearest inch.
6. What is the circumference of the top
of an ice cream cone if its diameter is
7
about 1 inches? C 6 in.
7. The radius of the basketball rim is
9 inches. What is the circumference?
C 57 in.
8
© Glencoe/McGraw-Hill
471
Geometry: Concepts and Applications
11–5
NAME
DATE
PERIOD
Skills Practice
Circumference of a Circle
Find the circumference of each object to the nearest tenth.
1. a round swimming pool
with radius 12 feet
75.4 ft
2. a circular top of a
trampoline with
diameter 16 feet
50.3 ft
4. a CD with diameter
11 centimeters
34.6 cm
3. the circular base of a
paper weight with
diameter 3 centimeters
9.4 cm
5. circular garden with
radius 10 feet
62.8 ft
6. circular mirror with
diameter 4 feet
12.6 ft
Find the circumference of each circle to the nearest tenth.
7. r 7 cm
8. d 20 yd
9. r 1 m
10. d 6 ft
11. r 200 ft
12. d 5 in.
13. r 2 m
14. d 70 ft
15. r 3 in.
16. d 10 in.
17. r 19 m
18. d 35 yd
44.0 cm
18.8 ft
12.6 m
31.4 in.
62.8 yd
1256.6 ft
219.9 ft
119.4 m
6.3 m
15.7 in.
18.8 in.
110.0 yd
Find the radius of each circle to the nearest tenth for each circumference given.
19. 100 m
15.9 m
22. 28 cm
4.5 cm
25. 75 yd
11.9 yd
© Glencoe/McGraw-Hill
20. 32 ft
21. 18 mi
5.1 ft
2.9 mi
23. 80 in.
24. 25 m
12.7 in.
26. 14 cm
4.0 m
27. 250 ft
2.2 cm
472
39.8 ft
Geometry: Concepts and Applications
11–5
NAME
DATE
PERIOD
Practice
Circumference of a Circle
Find the circumference of a circle with a radius of the given
length. Round your answers to the nearest tenth.
1. 3 cm 18.8 cm
2. 2 ft 12.6 ft
3. 34 mm 213.6 mm
4. 4.5 m 28.3 m
5. 6 cm 37.7 cm
6. 5 miles
31.4 miles
Find the exact circumference of each circle.
7.
14 in.
9.
52
in.
8.
26 cm
10.
16 cm
8 cm
© Glencoe/McGraw-Hill
473
Geometry: Concepts and Applications
11–5
NAME
DATE
PERIOD
Reading to Learn Mathematics
Circumference of a Circle
Key Terms
circumference (sir•KUM•fur•ents) the distance around a circle
pi () a Greek letter that represents the ratio of the
circumference of a circle to its diameter
Reading the Lesson
1. State whether each statement is true or false. If the statement is false,
explain why.
a. The number is an irrational number. true
b. If you know the diameter of a circle, you can find the circumference by using
the formula C 2d. False; the formula is C d.
c. The distance around a circle is called the circumference. true
d. By definition, the ratio of the circumference of a circle to the radius is pi.
False; the ratio of the circumference to the diameter is pi.
2. For the following exercises, use the given information to find the required
measure. Round the measure to the nearest tenth. Show how you find the
measure.
a. Find the circumference of a circle with a radius of 6 feet. Use the formula
C 2r, since the radius is given. The circumference is 2 • • 6,
which is approximately 37.7 feet.
b. Find the circumference of a circle with a diameter of 15 inches. Use the
formula C d, since the diameter is given. The circumference is
15, which is approximately 47.1 inches.
c. Find the radius of a circle with a circumference of approximately 163.4
centimeters. Use the formula C 2r. Substitue 163.4 for the
circumference and solve for r. So, C = 2r, 163.4 = 2r, 81.7 r,
r 81.7 or about 26 centimeters.
Helping You Remember
3. Write several sentences explaining the similarities and differences between the
perimeter of a polygon and the circumference of a circle. Be sure to mention the
formulas used to find these measures. Sample answer: The perimeter of a
polygon and the circumference of a polygon are similar in that they
are both the distance around a figure. They are different in that the
perimeter of a polygon involves measuring segments, while the
circumference of a circle is curved. The formula for perimeter of a
polygon uses addition of the lengths of the segments that are sides.
The formula for the circumference of a circle involves multiplying
the diameter by .
© Glencoe/McGraw-Hill
474
Geometry: Concepts and Applications
NAME
11–5
DATE
PERIOD
Enrichment
Finding Perimeter
Use a calculator to find the perimeter (the solid lines and
curves) of each figure. Use 3.14.
1.
2.
18 mm
24 m
5 mm
18.5 m
77.045 m
51.7 m
3.
4.
29 cm
8 cm
24.5 ft
153.86 ft
83.12 cm
5.
6.
35.8 m
7.7 m
24 in.
113.04 in.
7.
6.4 m
92.1 m
8.
14 yd
15 yd
9 yd
12 m
12 yd
78.82 yd
37.68 m
9.
10.
9 ft
6 ft
34 mm
94.2 ft
266.9 mm
© Glencoe/McGraw-Hill
475
Geometry: Concepts and Applications
11–6
NAME
DATE
PERIOD
Study Guide
Area of a Circle
The area A of a circle equals times the radius r squared: A r2.
Examples
1 Find the area of the circle.
A r2
2
A 13 2
A (42.25)
A 132.73
The area of the circle is about 132.7 in2.
2 Find the area of the shaded region.
Assume that the smaller circles are congruent.
Find the area of
the large circle.
Find the area of
a small circle.
A r2
A (20)2
A 1256.64
A r2
A (6)2
A 113.10
Now find the area of the shaded region.
A 1256.64 3(113.10)
1256.64 339.3
917.34
The area of the shaded region is about 917.3 m2.
Find the area of each circle to the nearest tenth.
1.
2.
153.9 ft2
3.
38.5 mm2
176.7 yd2
Find the area of each shaded region to the nearest tenth.
4.
5.
603.2 in2
© Glencoe/McGraw-Hill
6.
685.8 cm2
476
1,284.8 m2
Geometry: Concepts and Applications
NAME
11–6
DATE
PERIOD
Skills Practice
Area of a Circle
Find the area of each circle to the nearest hundredth.
1. r 10 in.
314.16 in2
4. d 50 ft
1963.50 ft
3. r 4 mm
5. d 6 in.
6. d 30 m
1017.88 cm2
2
7. C 31.42 yd
78.56 yd2
10. r 1 mi
2. r 18 cm
2
3.14 mi
13. d 300 ft
70,685.83 ft2
2
706.86 m2
28.27 in
8. C 131.95 m
1385.51 m2
11. d 90 m
2
6361.73 m
14. r 6 in.
113.10 in2
50.27 mm2
9. C 232.48 ft
4300.92 ft2
12. C 628.32 ft
31,416.07 ft2
15. C 150.80 m
1809.64 m2
A circle has a radius of 10 inches. Find the area of a sector whose central angle has
the following measure. Round to the nearest hundredth.
16. 90°
17. 30°
78.54 in2
19. 45°
18. 120°
26.18 in2
20. 60°
2
39.27 in
22. 100°
87.27 in2
© Glencoe/McGraw-Hill
104.72 in2
21. 135°
2
52.36 in
23. 150°
117.81 in2
24. 70°
130.90 in2
477
61.09 in2
Geometry: Concepts and Applications
11–6
NAME
DATE
PERIOD
Practice
Area of a Circle
Find the area of each circle described. Round your answers to the
nearest hundredth.
1. r 3 cm
28.27 cm2
4. d 13 ft
132.73 ft2
7. C 80 mm
509.30
mm2
2. r 31 ft
2
3. r 2.3 mm
38.48 ft2
5. d 22 mi
3
16.62 mm2
6. d 6.42 in.
5.59 mi2
8. C 15.54 in.
19.22
32.37 in2
9. C 121 mi
2
in2
12.43 mi2
In a circle with radius of 5 cm, find the area of a sector whose
central angle has the following measure. Round to the nearest
hundredth.
8. 10
2.18 cm2
11. 12
2.62 cm2
© Glencoe/McGraw-Hill
9. 180
10. 36
39.27 cm2
12. 120
7.85 cm2
13. 45
26.18 cm2
478
9.82 cm2
Geometry: Concepts and Applications
11–6
NAME
DATE
PERIOD
Reading to Learn Mathematics
Area of a Circle
Key Terms
sector a region of a circle bounded by a central angle and its
corresponding arc
Reading the Lesson
1. Complete each sentence.
N
(r2)
a. If a sector of a circle has an area of A square units, a central
360
angle measurement of N degrees, and radius of r units then A __________
.
b. The area of a geometric figure, such as a circle, is always expressed in
square units.
___________
r 2 .
c. If a circle has an area of A square units and a radius of r units, then A _____
360 .
d. The sum of the measures of the central angles of a circle is _____
sector of a circle is a region bounded by a central angle and its
e. A(n) __________
corresponding arc.
2. Suppose A has a circumference of 36 feet. Find the area of the circle to the
nearest tenth. Explain how you find the area and justify the steps you take.
To find the area, first use the value of the circumference to find
the radius. Then use the radius to find the area. By Theorem 11-7,
C 2r. Substitute the value for circumference to form an equation
to get 36 2r. Solve for r to get r 18. By Theorem 11-8, A r2.
Substitute the value for r to find the area, A (18)2. Use a calculator
and round the answer, A 1017.9 square feet.
3. Find the area of the shaded region in O to
the nearest hundredth. Explain your
method for finding the area.
O 135°
10 m
By Theorem 11-9, the area of a sector is
N
A (r2). Substituting the values from the diagram,
360
135
3
A ()(10)2. Simplifying, A • 100.
360
8
Using a calculator and rounding, A 117.8 square meters.
Helping You Remember
4. A good way to remember something is to explain it to someone else. Suppose your
classmate Adrienne is having trouble remembering which formula is for
circumference and which is for area of a circle. How can you help her? Sample
answer: Circumference is measured in linear units, while area is
square units, so the formula containing r2 must be the one for area.
© Glencoe/McGraw-Hill
479
Geometry: Concepts and Applications
11–6
NAME
DATE
PERIOD
Enrichment
Area of Circular Regions
Robin is going to fix a chain to tie up his dog Rover. There are
several places in the yard that Robin can attach the end of the
chain. For each of the following, use a compass to draw the
space that Rover can reach while on the end of a 12-foot chain.
Then find the area.
1. Rover’s chain is attached to a
stake in the middle of the yard.
area 144 ft2
2. Rover’s chain is attached to a
long wall.
area 72 ft2
12 ft
12 ft
3. Rover’s chain is attached to the
corner of the house.
area 108 ft2
4. Rover’s chain is attached to a
4-foot by 18-foot rectangular shed.
area 124 ft2
18 ft
4 ft
12 ft
12 ft
© Glencoe/McGraw-Hill
480
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Test, Form 1A
Write the letter for the correct answer in the blank at the right of each
problem.
For Questions 1–2, refer to the figure at the right.
A
D
1. Which statement is true?
X
D
is a diameter of X.
A. A
B. B
D
is a chord of X.
is a radius of X.
C. CD
D. X
D
is a chord of X.
B
1.
C
2. If BD 28.4 centimeters, find the radius of X.
A. 14.2 cm
B. 14.4 cm
C. 28.4 cm
3. Refer to the figure at the right. If A has radius 7.4,
B has radius 18.3, and AX 2.9, find BY.
A. 10.9
B. 13.8
C. 15.4
D. 21.2
C. major arc.
5. Find mLM .
A. 112
B. minor arc.
6. Which statement is false?
A. mMN mKL
C. mJK mJM 180
B
3.
J
K
N
68
44
S
L
D. central arc.
B. 126
Y
A
X
For Questions 4–6, refer to the figure at the right.
and M
K
are diameters of S.
In the figure, LN
4. JML is a
A. semicircle.
2.
D. 56.8 cm
C. 136
M
4.
5.
D. 224
B. mJN 78
D. mLNM 360 mLM
6.
7. The measure of a major arc is
A. less than 180.
B. equal to the measure of its corresponding minor arc.
C. equal to 180 plus the measure of its corresponding minor arc.
7.
D. equal to 360 minus the measure of its corresponding minor arc.
For Questions 8–10, refer to the figure at the right.
⊥
AC
.
In the figure, BD
8. If AB BC , then which segments are congruent?
B
and B
C
A. A
B. B
D
and A
C
C. A
F
and C
E
D. E
F
and D
E
B
F
A
B. 11.8
C
8.
D
9. If CE 11.8, find AC.
A. 5.9
E
C. 17.7
D. 23.6
C. 25
D. 40
9.
10. If AF 25 and AC 40, find DE.
A. 10
©
Glencoe/McGraw-Hill
B. 15
481
10.
Geometry: Concepts and Applications
NAME
11
DATE
PERIOD
Chapter 11 Test, Form 1A (continued)
11. A chord of a circle is 30 feet long. If the diameter of the circle is 34 feet,
what is the distance from the center of the circle to the chord?
A. 5 ft
B. 8 ft
C. 15 ft
D. 17 ft
12. Refer to the figure at the right. If AB 4d 10 and
CD 6d 14, find d.
A. 2
B. 8
C. 12
11.
B
A
D
D. 24
d
d
C
12.
13. Regular hexagon ABCDEF is inscribed in P. Which statement is not true?
A. The angles of the polygon are central angles of the circle.
B. The sides of the polygon are chords of the circle.
C. Some of the diagonals of the polygon are diameters of the circle.
D. The perimeter of the polygon is less than the circumference of P.
13.
14. If the diameter of a circle is 8.5 kilometers, find the circumference of the
circle to the nearest tenth.
A. 13.4 km
B. 26.7 km
C. 39.4 km
D. 53.4 km
14.
15. Find the radius of the quarter circle shown at the right if the
length of AB is 32 yards.
A. 5.1 yd
B. 10.2 yd
C. 15.3 yd
D. 20.4 yd
B
r
15.
A
16. About how many revolutions must a 20-inch-diameter wheel make in
order to travel a distance of 100 feet?
1
A. 1 2
1
C. 9 2
B. 5
D. 19
16.
17. To the nearest tenth, find the area of a circle with radius 7.2 kilometers.
A. 45.2 km2
B. 162.9 km2
C. 372.1 km2
D. 511.6 km2
17.
18. To the nearest tenth, what is the area of a circle with circumference
35.6 centimeters?
A. 100.9 cm2
B. 211.8 cm2
C. 316.8 cm2
D. 403.4 cm2
19. Find the area of the shaded sector of S shown at the right.
Round the area to the nearest hundredth.
2
A. 4.40 ft
C. 48.62
ft2
B. 8.80
B. 12.5 in.
12 ft
S
ft2
19.
20. Suppose the circle at the right has a radius of 10 inches. To
the nearest tenth, what must be the side length of the shaded
square if the probability that a randomly-thrown dart that
lands inside the circle hits the shaded region is 0.5?
A. 10 in.
42
ft2
D. 52.78
18.
C. 15 in.
s
s
D. 17.5 in.
20.
Bonus Suppose a chord of a circle is 12 millimeters long and is 3 millimeters
from the center of the circle. What is the area of the circle?
A. 45 mm2
©
Glencoe/McGraw-Hill
B. 54 mm2
C. 90 mm2
482
D. 153 mm2
Bonus
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Test, Form 1B
Write the letter for the correct answer in the blank at the right of each
problem.
For Questions 1–2, refer to the figure at the right.
Y
Z
1. Which statement is false?
Z
is a diameter of P.
A. X
B. X
Y
is a chord of P.
Z
is a chord of P.
C. P
D. PX
is a radius of P.
P
1.
X
2. If PY 22 centimeters, find the diameter of P.
A. 11 cm
B. 22 cm
C. 33 cm
2.
D. 44 cm
3. Point A is the center of both circles shown at the right.
If the diameters of the circles are 8 inches and 18 inches,
find BC.
A. 5 in.
B. 7 in.
C. 10 in.
A
C
D. 13 in.
For Questions 4–6, refer to the figure at the right.
In the figure, AC
is a diameter of R.
4. ABC is a
A. major arc.
C. minor arc.
5. Find mBD.
A. 105
B
3.
A
B
R
B. semicircle.
65
40
D. central arc.
4.
D
C
B. 125
6. Which statement is false?
A. mADC mABC
C. mAD 140
D. 155
5.
B. mAB mBC 180
D. mABD 360 mAB
6.
C. 140
7. The measure of a minor arc is
A. equal to the measure of its corresponding major arc.
B. equal to the measure of its central angle
C. equal to 360 plus the measure of its corresponding major arc.
7.
D. greater than 180.
For Questions 8–10, refer to the figure at the right.
⊥
MP
.
In the figure, SN
MP
, then which arcs are congruent?
8. If ML
B. LM and LP
A. LP and MP
C. LM and MP
D. LM and MN
L
S
M
Q
N
9. If MP 64, find QP.
A. 16
B. 32
C. 64
P
8.
D. 128
9.
D. 51.2
10.
10. If SQ 9 and MP 24, find the diameter of S.
A. 15
©
Glencoe/McGraw-Hill
B. 25.6
C. 30
483
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Test, Form 1B (continued)
11. A chord of a circle is 9 inches long and its midpoint is 6 inches from the
center of the circle. What is the radius of the circle?
A. 6.5 in.
B. 7.5 in.
C. 10.5 in.
12. Refer to the figure at the right. If HJ 3x and
KL 5x 6, find the value of x.
A. 2
B. 3
C. 4
D. 6
D. 10.8 in.
11.
J
H
x
x
K
12.
L
13. Complete: A pentagon is inscribed in a circle if and only if every
the pentagon lies on the circle.
A. vertex
B. side
C. point
?
of
D. angle
13.
14. If the radius of a circle is 6 feet, find the circumference of the circle to the
nearest tenth.
A. 18.8 ft
B. 25.4 ft
C. 37.7 ft
15. In the figure at the right, XY is a semicircle. If
mXY 15 meters, find XY to the nearest tenth.
A. 2.4 m
B. 4.8 m
C. 7.2 m
D. 9.5 m
D. 41.9 ft
14.
X
Y
15.
16. A wheel has a radius of 1 foot. To the nearest foot, how far will the wheel
travel in 50 revolutions?
A. 157 ft
B. 235 ft
C. 314 ft
D. 628 ft
16.
17. Find the area of a circle with radius 3 yards. Round to the nearest tenth.
A. 9.4 yd2
B. 28.3 yd2
C. 58.5 yd2
D. 88.8 yd2
17.
18. To the nearest tenth, what is the area of a circle with circumference
18 centimeters?
A. 28.3 cm2
B. 254.5 cm2
C. 682.4 cm2
D. 1017.9 cm2
19. Find the area of the shaded sector of C shown at the right.
Round the area to the nearest hundredth.
A. 47.45 m2
B. 31.72 m2
C. 43.63 m2
D. 52.54 m2
5m
C 160
19.
20. Find the probability that a randomly-thrown dart will hit
the shaded region of the target shown at the right. Assume
that the dart lands somewhere inside the circle. Round to
the nearest hundredth.
A. 0.32
B. 0.34
18.
C. 0.36
8
D. 0.38
20.
Bonus Suppose a chord of a circle is 32 millimeters long and is 12 millimeters
from the center of the circle. What is the circumference of the circle?
A. 10 mm
©
Glencoe/McGraw-Hill
B. 20 mm
C. 30 mm
484
D. 40 mm
Bonus
Geometry: Concepts and Applications
NAME
11
DATE
PERIOD
Chapter 11 Test, Form 2A
For Questions 1–2, refer to the figure
shown at the right.
1. Name two chords of Q.
V
U
R
1.
Q
1
2. If SU 13 , find the measure of a
2
radius of Q.
T
S
3. In the figure at the right, A has
diameter 18 and B has diameter 10.
If BD 2, find AC.
A
C
2.
D B
3.
For Questions 4– 6, refer to the figure shown
at the right.
A
4. Name three minor arcs that have E as one
endpoint. Find the measure of each arc.
5. True or false: AEC is a minor arc. If false,
change the underlined word to make a
true statement.
6. In P, AD
and B
E
are diameters. Find mAC.
B
C
36
P
4.
42
E
D
5.
6.
7. Complete: You find the degree measure of a major arc by
subtracting the degree measure of the corresponding ?
from ? .
For Questions 8–10, refer to the figure
shown at the right.
8. If ED
EG
, then EDG is congruent to
which arc?
7.
G
D
C
H
F
8.
1
9. If EG 19 2 , find HG.
E
9.
10. If CH 30 and the radius of C is 34,
find EG.
10.
11. Suppose a chord in a circle is 48 centimeters long and it is
7 centimeters from the center of the circle. Find the length of
a radius of the circle.
11.
12. Complete: If pentagon ABCDE is inscribed in S, then A
B
is
?
?
a
of S and A
S
is a
.
12.
©
Glencoe/McGraw-Hill
485
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Test, Form 2A (continued)
13. In the figure at the right, if AB 5x 14
and CD 2x 7, find the value of x.
D
x
A
x
C
B
13.
14. Find the diameter of a circle with circumference 23 inches.
1
Round to the nearest 4 -inch.
14.
15. The figure at the right is formed by placing a
semicircle on top of a rectangle. To the nearest
foot, what is the distance around the outer
edge of the figure?
10 ft
6 ft
15.
16. About how many revolutions must a 4-foot-diameter wheel
make in order to travel 200 yards?
16.
17. Find the area of a circle with radius 48 centimeters. Round to
the nearest square centimeter.
17.
18. Find the area of a circle with circumference 60 millimeters.
Round to the nearest tenth.
18.
19. What is the area of the shaded sector shown
in the figure at the right? Round to the
nearest square foot.
110
8 ft
19.
20. If the diameter of the circle shown at the
right is 12 inches and the length of each side
of the four congruent squares is 3 inches,
what is the probability (to the nearest whole
percent) that a randomly-thrown dart that
lands inside the circle will land in one of the
shaded squares?
20.
Bonus A chord 20 meters long is drawn in a circle whose area is
144 square meters. What is the distance from the chord to the
Bonus
center of the circle? Round to the nearest tenth.
©
Glencoe/McGraw-Hill
486
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Test, Form 2B
For Questions 1–2, refer to the figure
shown at the right.
D
C
X
1. Name a diameter of X.
1.
A
2. If AC 14.2, find the measure of a
radius of X.
2.
B
3. In the figure at the right, point A is
the center of both circles, and C
D
and
EF
are diameters. If AB 3 and
EF 20, find DF.
E
C
B
A
D
3.
F
For Questions 4– 6, refer to the figure
shown at the right.
L
S
4. Name three major arcs that have M as one
endpoint. Find the measure of each arc.
P
80 30
5. True or false: LPN is a major arc. If false,
change the underlined word to make a
true statement.
6. In S, LN
is a diameter. Find mLM .
4.
N
M
5.
6.
7. Complete: The degree measure of a minor arc is equal to the
degree measure of its ? .
For Questions 8–10, refer to the figure shown
at the right.
8. If EF BD , name a segment that is
congruent to BD
.
7.
E
F
A
G
9. If AC
⊥
BD
and BD 26, find GD.
B
8.
D
9.
C
10. If AC
⊥
BD
, AB 26, and BD 48,
find AG.
10.
11. Suppose a chord in a circle is 80 centimeters long and it is
30 centimeters from the center of the circle. Find the measure
of a radius of the circle.
11.
12. True or false: A polygon is inscribed in a circle if all sides of
the polygon lie inside the circle. If false, change the
underlined words to make a true statement.
12.
©
Glencoe/McGraw-Hill
487
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Test, Form 2B (continued)
13. In the figure at the right, if PQ 2d 10
and RS 4d, find the value of d.
Q
P
d
R
d
S
13.
14. Find the radius of a circle with circumference 25 feet. Round
to the nearest tenth.
15. In the figure at the right, AC
⊥
BC
and
AC 15 meters. Find the length of
AB to the nearest meter.
14.
C
B
15 m
A
15.
1
16. To the nearest foot, how far will a wheel of radius 1 feet
2
travel in 50 revolutions?
16.
17. Find the area of a circle with diameter 16 millimeters. Round
to the nearest square millimeter.
17.
18. Find the area of a circle with circumference 10 meters.
Round to the nearest tenth.
18.
19. What is the area of the shaded sector
shown in the figure at the right? Round to
the nearest square yard.
6 yd
60
19.
20. In the figure at the right, each of the four
circles has a radius of 2.5 feet. If each circle
just touches two other circles as well as two
sides of the square, what is the probability
(to the nearest whole percent) that a
randomly-thrown dart that lands inside the
square will land in one of the shaded circles?
Bonus A chord 12 centimeters long is drawn in a circle whose
area is 100 square centimeters. What is the distance from
the chord to the center of the circle?
©
Glencoe/McGraw-Hill
488
20.
Bonus
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Extended Response Assessment
Instructions: Demonstrate your knowledge by giving a clear, concise
solution for each problem. Be sure to include all relevant drawings
and to justify your answers. You may show your solution in more
than one way or investigate beyond the requirements of the problem.
1. A and B overlap as shown at the
right. The radius of A is 6 centimeters
and the radius of B is 10 centimeters.
If the radii of the circles contained in A
B
overlap by 2 centimeters as shown in the
figure at the right, find AB.
2 cm
A
B
2. On a separate sheet of 8.5 in. 14 in. paper (or larger), construct
the two circles described and shown in Question 1. Draw the figure
full scale (using the actual centimeter measures). Be sure to place
points A and B so their locations agree with the value of AB you
found in Question 1. In your figure, label the point where
A intersects A
B
as point P, and label the point where B
as point Q. Label the points where the two circles
intersects AB
intersect as points C and D. Finally, draw C
D
and label the
intersection of A
B
and C
D
as point M.
C
, B
C
, A
D
, and BD
.
3. On your figure, draw A
a. Is ABC ABD? Justify your answer.
b. Is CAP PAD? Justify your answer.
c. Find mAMC.
4. Shade the petal-shaped region bounded by CD on A and CD
on B.
, B
M
, and CD
to the nearest
a. Use a metric ruler to measure AM
tenth of a centimeter.
b. Use your values for AM and CD to find the area of ACD.
c. Use your values for BM and CD to find the area of BCD.
d. Use a protractor to measure CAD. Find the area of the sector
of A bounded by CAD. Round to the nearest hundredth.
e. Use a protractor to measure CBD. Find the area of the sector
of B bounded by CBD. Round to the nearest hundredth.
f. Use your results from parts b and d to find the area of the
D
and CD on A.
region between C
g. Use your results from parts c and e to find the area of the
and CD on B.
region between CD
h. Use your results from parts f and g to find the area of the
shaded region that is the overlap of A and B.
©
Glencoe/McGraw-Hill
489
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Mid-Chapter Test
(Lessons 11–1 through 11–3)
For Questions 1–4, refer to the figure shown
at the right.
E
D
For Questions 1–3, determine whether each
statement is true or false.
A
is a chord of A.
1. BD
C
B
1.
2. AC 2(BD)
2.
3. A has twice as many diameters as radii.
3.
4. If BD 7.8, find AE.
4.
5. In the figure at the right, X has
radius 16 and Y has radius 10.
If CD 5.5, find AB.
X
A
Y
C
B
D
5.
For Questions 6–8, refer to the figure shown
at the right. P
R
and Q
T
are diameters of C.
6. Find mPS .
7. Find mPSQ .
8. Find mQST .
P
T
6.
C
7.
38 42
Q
8.
S
R
9. True or false: The degree measure of a major arc equals 180 the degree measure of the corresponding minor arc. If false,
change the underlined expression to make a true statement.
For Questions 10–13, refer to the figure shown
at the right. In the figure, AC
⊥
BD
.
10. If BD DE , then ABD ? .
D
11. If BD 26, find BG.
12. If AG 6 and BG 10, find CG. Round
to the nearest tenth.
C
B
G
10.
A
E
13. If the radius of A is 25 and BD 40, find AG.
14. Suppose a chord of a circle is 18 inches long and it is
40 inches from the center of the circle. Find the length of a
radius of the circle.
©
Glencoe/McGraw-Hill
490
9.
11.
12.
13.
14.
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Quiz A
(Lessons 11–1 and 11–2)
For Questions 1–5, refer to the figure shown
at the right. In the figure, CF
is a diameter
of A.
F
E
B
1. Name three radii of A.
A
1.
D
2. Complete: E
D
is a
?
of A.
2.
C
3. If CF 25, find AB.
3.
4. If mBAF 58, what is mBC ?
4.
5. How would you use a central angle to find mBFC ?
For Questions 6–8, refer to the figure shown
at the right in which KM
and J
L
are diameters
of X. Find the measure of each arc.
6. KLN
J
7. JN
K
8. KLM
11
5.
N
M
27
L
42 X
6.
7.
8.
NAME
DATE
PERIOD
Chapter 11 Quiz B
(Lessons 11–3 through 11–6)
For Questions 1–2, refer to the figure shown at
the right. In the figure, LN
⊥
PM
.
N
P
Q
X
1. If MQ 4.6, find MP.
M
2. If PM 8 and XQ 3, find the radius of X.
1.
2.
L
3. Refer to the figure shown at the right. If
WX 6d 14 and BY d 3, find CX.
Z
B
W
A
Y
C
X
4. Find the circumference of a circle with radius 11 feet. Round to
the nearest tenth.
3.
4.
5. Find the area of the shaded sector of C
at the right. Round to the nearest tenth.
150 C
8m
5.
©
Glencoe/McGraw-Hill
491
Geometry: Concepts and Applications
NAME
11
DATE
PERIOD
Chapter 11 Cumulative Review
1. Is the converse of the statement below true or false? If false,
draw a counterexample. (Lessons 1–4, 8–4)
The diagonals of a square are perpendicular.
1.
2. Write an equation for the horizontal line that passes through
the midpoint of the segment connecting A(2, 6) and
B(4, 10). (Lessons 2–4, 2–5)
2.
3. In the figure at the right, AD ⊥ BE . Find
m1 and classify it as acute, right, or
obtuse. (Lessons 3–2, 3–5, 3–6, 3–7)
E
D
X
F
33
1
C
B
A
3.
4. Refer to the figure at the right. Find the
value of x so that a b. (Lesson 4–4)
a
50
c
(3x + 16)
b
4.
5. Classify XYZ by its angles and sides if mX 36 and
mZ 54. (Lessons 5–1, 5–2)
5.
6. PX
and R
Y
are medians of PQR intersecting at point Z. If
RZ 22, find RY. (Lesson 6–1)
6.
7. List the angles of SRT in order from least to
greatest measure. (Lesson 7–3)
R
13
8
S
11
T
8. Find mA in rhombus ABCD if mCBD 40. (Lesson 8–4)
15
7.
8.
5
9. Solve . (Lesson 9–1)
12
5x 4
9.
10. Suppose ABC DEF and the scale factor of ABC to
DEF is 4 : 5. If the perimeter of ABC is 72 feet, what is the
perimeter of DEF? (Lesson 9–7)
10.
11. Find the perimeter of a regular nonagon whose sides are
6.8 millimeters long. (Lesson 10–1)
11.
12. Find the area of the regular octagon with apothem 14.5 feet
long and side length 12 feet. (Lesson 10–5)
12.
13. Suppose a chord of a circle is 32 meters long and it is
30 meters from the center of the circle. Find the diameter of
the circle. (Lesson 11–3)
13.
14. Find the circumference of a circle with area 49 square
inches. Round to the nearest tenth. (Lessons 11–5, 11–6)
14.
©
Glencoe/McGraw-Hill
492
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Standardized Test Practice
(Chapters 1–11)
Write the letter for the correct answer in the blank at the right of each
problem.
1. The intersection of two rays cannot be a
A. point.
B. line.
C. segment.
1.
D. ray.
2. Identify the converse of the statement below.
All squares have congruent sides.
A. If a quadrilateral has congruent sides, then it is a square.
B. No squares have sides that are congruent.
C. If a quadrilateral is a square, then it has congruent sides.
2.
D. A rhombus has congruent sides.
3. Points X, Y, and Z are collinear, with point X between points Y and Z.
If XY 11.9 and YZ 12.4, find XZ.
A. 0.5
3.
C. 23.3
D. 24.3
bisects BXD,
4. Refer to the figure at the right. If XC
B
A
mBXC 31, and mAXB 45, find mAXD.
A. 14
B. 1.5
B. 76
C. 107
C
D. 117
X
4.
D
5. Vertical angles are always
A. complementary.
B. supplementary.
C. adjacent.
D. congruent.
5.
p
6. Refer to the figure at the right. Which congruence
cannot be used to justify that p q ?
A. 1 7
B. 2 4
C. 4 8
D. 3 5
1 2
4 3
q
56
8 7
m
6.
7. What is the slope of the line passing through A(4, 2) and B(1, 6)?
3
A. 8
5
B. 8
8
C. 5
8
D. 3
7.
D. 123
8.
8. In ABC, find mB if mA 24.9 and mC 36.1.
A. 46.1
B. 109
C. 119
9. In the figure at the right, which triangle is a
translation of triangle 5?
A. triangle 1
B. triangle 2
C. triangle 3
D. triangle 4
y
5
1
2
4
3
x
9.
10. Which statement is always true about isosceles triangles?
A. The median from a base angle is an angle bisector.
B. The measure of the vertex angle is less than the measure of each base
angle.
C. The two congruent sides form a base angle.
D. The median from the vertex angle bisects that angle.
©
Glencoe/McGraw-Hill
493
10.
Geometry: Concepts and Applications
11
NAME
DATE
PERIOD
Chapter 11 Standardized Test Practice
(Chapters 1–11) (continued)
11. In a right triangle, the measures of the legs are 12 and 5. What is the
measure of the hypotenuse?
A. 7
B. 10.9
C. 11
11.
D. 13
12. Which set of three numbers cannot be the measures of the sides of
a triangle?
A. 2, 5, 8
B. 7, 7, 8
C. 12, 14, 22
12.
D. 4, 8, 11
13. Refer to the figure at the right. Which of the following
statements can be used to prove that quadrilateral
ABCD is a parallelogram?
A
B
X
A. BD AC
B. AB CD and ABC BCD
D
C
C. ADB CBD
D. AB CD and BAC ACD
13.
R
and S
T
are the bases. Which statement
14. In isosceles trapezoid QRST, Q
is true?
1
A. The length of the median of the trapezoid is 2 (RS QT ).
T
is a diagonal of the trapezoid.
B. Q
C. QT RS
D. R S
14.
15. Which statement about similar polygons is not true?
A. All rectangles are similar.
B. All equilateral triangles are similar.
C. All regular hexagons are similar.
15.
D. All isosceles right triangles are similar.
16. Suppose JKL TRS. If RT 12, JK 20, and ST 21, find JL.
A. 33
B. 35
C. 39
D. 42
16.
D. 1080
17.
17. What is the sum of the interior angles of a heptagon?
A. 360
B. 720
C. 900
18. Find the area of the trapezoid shown at the right.
A. 81 m2
B. 90 m2
C. 148 m2
D. 162 m2
12 m
6m
15 m
18.
19. In a circle with radius 26 inches, a chord is drawn that is 10 inches from
the center of the circle. How long is this chord?
A. 12 in.
B. 24 in.
C. 48 in.
D. 60 in.
19.
20. What is the area of a circle that has a diameter 24 centimeters
A. 48 cm2
©
Glencoe/McGraw-Hill
B. 64 cm2
C. 96 cm2
494
D. 144 cm2
20.
Geometry: Concepts and Applications
Preparing for Standardized Tests
Answer Sheet
1.
A
B
C
D
E
2.
A
B
C
D
E
3.
A
B
C
D
E
4.
A
B
C
D
E
5.
A
B
C
D
E
6.
A
B
C
D
E
7.
A
B
C
D
E
8.
A
B
C
D
E
9.
/
/
•
•
•
•
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
0
1
2
3
4
5
6
7
8
9
10. Show your work.
© Glencoe/McGraw-Hill
A1
Geometry: Concepts and Applications
Study Guide
NAME
© Glencoe/McGraw-Hill
䉺F

CF
苶, or 苶
BF
苶
AF , 苶
• Name a chord that is not a diameter.
• Name a radius.
• Name the circle.
苶 is a diameter.
In 䉺F, 苶
AC
A2
false
false
true
true
© Glencoe/McGraw-Hill
451
苶 is 1 inch long.
9. 䉺G has a diameter of 2 inches. Chord 苶
BC
苶 is a diameter.
8. 䉺A has a radius of 2 inches. 苶
QR
On a separate sheet of paper, use a compass and a
ruler to make a drawing that fits each description.
8-9. See students’ work.
7. If PB = 7, then AC = 14.
6. 苶
AC
苶 is a chord of 䉺P. true
苶 is a radius of 䉺P. true
5. 苶
PC
Y
Z
© Glencoe/McGraw-Hill
20. If XY 7, find WR. 28
19. If XY 7, find TX. 23
18. If XY 7, find WX. 8
17. If XY 7, find YZ. 3
452
R
A
W
X W
B
X
S
Y
C
Z
U
T
PERIOD
R
Geometry: Concepts and Applications
T
Circle W has a radius of 15 units, and Z has a radius of 10 units.
16. B
苶U
苶 is a chord of 䉺A. false
15. Z
苶U
苶 is a radius of 䉺A. false
14. Z
苶U
苶 is a chord of 䉺A. true
13. SC SA false
12. S
苶Y
苶 is a chord of 䉺A. true
10. SU RX false
9. A
苶T
苶 is a chord of 䉺A. false
8. AT AZ true
7. S
苶W
苶 is a chord of 䉺A. true
6. S
苶W
苶 is a diameter of 䉺A. true
5. AT BX
4. SA SW
3. ZU 2(ZA)
2. 苶R
苶B
苶 is a chord of 䉺A. false
苶 is a radius of 䉺A. true
1. 苶
AT
4. a chord 苶
X苶
Y or 苶
R苶
T
Use P to determine whether each
statement is true or false.
DATE
Use A at the right to determine whether each statement is true or false.
11. SA AU true
苶
BC
苶
Skills Practice
NAME
Parts of a Circle
11–1
3. a diameter 苶
R苶
T
1. the center
S
  
2. three radii SR, SM, ST
Use S to name each of the following.
Example:
PERIOD
Geometry: Concepts and Applications
DATE
A circle is the set of all points in a plane that are a given
distance from a given point in the plane called the center.
Various parts of a circle are labeled in the figure at the right.
Note that the diameter is twice the radius.
Parts of a Circle
11–1
Answers
(Lesson 11-1)
Geometry: Concepts and Applications
Practice
NAME
© Glencoe/McGraw-Hill
苶D
A
苶, A
苶B
苶
4. Name two chords.
DATE
A3
true
true
© Glencoe/McGraw-Hill
12. PA PD
11. A
苶C
苶 is a diameter of circle P. true
10. A
苶B
苶 is a diameter of circle P. false
9. 苶
AB
苶 is a chord of circle P. true
8. 苶
PB
苶 is a chord of circle P. false
7. CA 2(PE)
6. 苶
AB
苶 is a radius of circle P. false
苶 is a radius of circle P. true
5. 苶
PB
453
PERIOD
Geometry: Concepts and Applications
Use circle P to determine whether each statement is true or false.
苶B
A
苶
3. Name a diameter.
苶A
P
苶, P
苶D
苶, P
苶B
苶
2. Name three radii of the circle.
1. Name the center of 䉺P. P
Refer to the figure at the right.
Parts of a Circle
11–1
PERIOD
iv. circle
© Glencoe/McGraw-Hill
454
Geometry: Concepts and Applications
first part comes from dia, which means across or through, as in
diagonal. The second part comes from metron, which means
measure, as in geometry.
3. A good way to remember a new geometric term is to relate the word or its parts
to geometric terms you already know. Look up the origins of the two parts of the
word diameter in a dictionary. Explain the meaning of each part and give a term
you already know that shares the origin of that part. Sample answer: The
Helping You Remember
iii. chord
d. a segment whose endpoints are the center and any point
on a circle i
ii. diameter
b. the set of all points in a plane that are the same distance
from a given point iv
c. a chord that passes through the center of a circle ii
i.
a. a segment whose endpoints are on a circle iii
radius
2. Match each description from the first column with the best term from the second
column. One term is used more than once.
center, then it is a diameter.
d. A chord of a circle is a diameter. Sometimes; if the chord contains the
c. A diameter of a circle is a chord. always
b. If you draw any two circles, they are similar. always
the measure of the radius of the circle.
a. The measure of the diamenter of a circle is one-half the measure of the radius
of the circle. Never; the measure of the diameter of a circle is twice
1. Tell whether each statement is always, sometimes, or never true. If the statement
is not always true, explain why.
Reading the Lesson
circle the set of all points in a plane that are a given distance
from a given point in the plane, called the center of the circle
radius (RAY•dee•us) a segment whose endpoints are the
center of the circle and a point on the circle
chord (CORD) a segment whose endpoints are on the circle
diameter a chord that contains the center of the circle
concentric circles that lie in the same plane, have the same
center, and have radii of different lengths
Key Terms
DATE
Reading to Learn Mathematics
NAME
Parts of a Circle
11–1
Answers
(Lesson 11-1)
Geometry: Concepts and Applications
11–2
Study Guide
NAME
© Glencoe/McGraw-Hill
Then, without changing
the compass setting,
move the point to a point
on the circle. Draw a
second circle.
Place the point on one
of the points where the
two circles intersect.
Draw a circle. Repeat
five more times.
A4
© Glencoe/McGraw-Hill
455
Geometry: Concepts and Applications
Use your compass and a straightedge to make a design like
the one below. (HINT: See the design above.) Check students’ drawings.
Use your compass to
draw a circle.
DATE
© Glencoe/McGraw-Hill
២ major; 260
3. mTSR
456
២ semicircle; 180
4. mMST
PERIOD
Geometry: Concepts and Applications
M苶
T are diameters
Refer to P for Exercises 1–4. If S
苶N
苶 and 苶
with m SPT 51 and m NPR 29, determine whether each
arc is a minor arc, a major arc, or a semicircle. Then find the
degree measure of each arc.
២
២ minor; 51
2. mST
1. mNR minor; 29
Since ⬔ ARB is a central angle and
២
m⬔ ARB 42, then mAB 42.
២
2 Find mACB.
២
mACB 360 m⬔ ARB 360 42 or 318
២
3 Find mCAB.
២ mABC
២ mAB
២
mCAB
180 42
222
AC
苶 is
Examples: In 䉺R, m⬔ ARB 42 and 苶
a diameter.
២.
1 Find mAB
You can use central angles to find the degree measure
of an arc. The arcs determined by a diameter are
called semicircles and have measures of 180.
An angle whose vertex is at the center of a circle is
called a central angle. A central angle separates a
circle into two arcs called a major arc and a minor
arc. In the circle at the right, ⬔ CEF is a central
angle. Points C and F and all points of the circle
interior to ⬔ CEF form a minor arc called arc CF.
២. Points C and F and all points of the
This is written CF
២
circle exterior to ⬔ CEF form a major arc called CGF .
PERIOD
Arcs and Central Angles
DATE
Many designs can be made using geometric constructions. Two
examples are stained glass rose windows found in churches and
Pennsylvania Dutch hex designs found on barns.
Enrichment
NAME
Constructing Designs
11–1
Answers
(Lessons 11-1 and 11-2)
Geometry: Concepts and Applications
Skills Practice
NAME
DATE
PERIOD
© Glencoe/McGraw-Hill
55
12. mABF 315
10. m⬔BCD
45
A
F
B
C
D
true
A5
false
false
B
E
C
A
28. mBD 90
27. mDS 115
© Glencoe/McGraw-Hill
26. mBSD 270
25. mAER 205
457
155
24. m⬔RQA
23. mAR 155
115
22. m⬔RQE
21. mAE 90
S
E
D
Q
B
A
D
E
Geometry: Concepts and Applications
R
Q is the center of two circles with radii 苶
Q苶
D and 苶
Q苶
E. If m⬔AQE 90 and mRE 115,
find each measure.
20. m⬔DAE mDE true
true
true
18. mBCD 180
19. mCE 145
false
17. mCED 220
16. m⬔BAC m⬔DAE
15. ⬔ABE is a central angle.
14. mCD m⬔CAD
13. m⬔BAC 60 true
In A, B
苶D
苶 is a diameter, m⬔BAE 85, and m⬔CAD 120. Determine whether each
statement is true or false.
11. mBAE 260
9. mDE 45
8. m⬔DCE
7. mAFE 180
100
135
3. m⬔FCE
6. m⬔BCE
4. mEF 135
45
1. m⬔ACF
5. mABE 180
2. mAB 80
Find each measure in C if mACB 80, mAF 45, and A
苶E
苶 and F
苶D
苶 are diameters.
Arcs and Central Angles
11–2
Practice
NAME
DATE
140
4. mABC
180
6
121
62
15. mDC
62
12. m⬔CPB
9. mAB 62
6. mAE 59
118
$ 7,945,177
4,204,099
12,645,630
145,367
760,616
$25,700,889
7. mED 59
© Glencoe/McGraw-Hill
458
PERIOD
Geometry: Concepts and Applications
b. Out of the $12,645,630 spent on post-secondary education,
$10,801,185 went to post-secondary financial assistance. What
percent is that of the $12,645,630? 85.4%
1990 Federal Funds
Spent for Education
16. mCEA 180
13. mCB 118
10. mEC 121
a. Use the information to make a circle graph.
Elementary/Secondary
Education for the Disabled
Post-Secondary Education
Public Library Services
Other
Total
1990 Federal Funds Spent for Education
17. The table below shows how federal
funds were spent on education in 1990.
14. mCEB 242
11. mEB
8. m⬔3
5. x
In P, m⬔2 m⬔1, m⬔2 4x 35, m⬔1 9x 5, and
苶
苶 and A
苶C
苶 are diameters. Find each of the following.
BD
3. mAB
In P, m1 140 and A
苶C
苶 is a diameter. Find each measure.
2. mBC 40
1. m⬔2 40
Arcs and Central Angles
11–2
Answers
(Lesson 11-2)
Geometry: Concepts and Applications
© Glencoe/McGraw-Hill
A6
D
A
52
P
B
PERIOD
C
© Glencoe/McGraw-Hill
459
C
Z
X
Y
Geometry: Concepts and Applications
minor arc, XZY is a major arc, and XYZ is a semicircle.
3. To help you remember terms in this lesson, sketch a circle. Label
and identify a minor arc, a major arc, and a semicircle.
Sample answer: In 䉺C with diameter 苶X
苶Z
苶, XY is a
Helping You Remember
major arc is 360 minus the degree measure of its central angle.
d. mDAC The measure is 360 90, or 270, because the measure of a
arc is the same as its central angle, which is a right angle.
c. mCD The measure is 90 because the degree measure of a minor
semicircle and mAB mBC mABC.
b. mBC The measure is 180 52, or 128, because ABC is a
arc is the degree measure of its central angle.
2. Refer to the figure in Exercise 1. Give each of the following arc measures. Explain
how you find the measure.
a. mAB The measure is 52 because the degree measure of a minor
d. ⬔BPC is an acute central angle. False; it is an obtuse central angle.
c. AD ⬵ CD true
its measure is less than 180.
b. ADC is a semicircle. true
1. Refer to 䉺P with diameter 苶
AC
苶. State whether each
statement is true or false. If the statement is false,
explain why.
a. DAB is a major arc. False; it is a minor arc because
Reading the Lesson
central angle an angle whose vertex is the center of a circle
and whose sides intersect the circle
arc a set of points along a circle defined by a central angle
minor arc a part of the circle in the interior of a central angle
that measures less than 180
major arc a part of the circle in the exterior of a central angle
that measures greater than 180
semicircle an arc whose endpoints lie on a diameter of a circle
adjacent arcs arcs of a circle with one point in common
Key Terms
DATE
Reading to Learn Mathematics
NAME
Arcs and Central Angles
11–2
Enrichment
NAME
DATE
4.6 cm
P
E
A
© Glencoe/McGraw-Hill
460
D
R
B
PERIOD
C
Q
Geometry: Concepts and Applications
6. Measure the width of the figure you made in Exercise 5.
Draw two parallel lines with the distance between them
equal to the width you found. On a piece of paper, trace the
five-sided figure and cut it out. Show that it will roll between
the lines drawn. 5.3 cm
Some countries use shapes like this for coins. They are useful
because they can be distinguished by touch, yet they will
work in vending machines because of their constant width.
Step 3: Continue this process until you
have five arcs drawn.
Step 2: Make another arc from B to C that
has center E.
Step 1: Place he point of your compass on
D with opening DA. Make an arc
with endpoints A and B.
5. Make a different curve of constant width by starting with the
five points below and following the steps given.
4. Trace the Reuleaux triangle above on a piece of paper and
cut it out. Make a square with sides the length you found in
Exercise 1. Show that you can turn the triangle inside the
square while keeping its sides in contact with the sides of
the square. See students’ work.
The Reuleaux triangle is made of three arcs. In the
២
example shown, PQ has center R, QR has center P, and
PR has center Q.
4.6 cm
3. What is the distance from R to the opposite side?
2. Find the distance from Q to the opposite side.
1. Use a metric ruler to find the distance from P to
any point on the opposite side. 4.6 cm
The figure at the right is called a Reuleaux triangle.
A circle is called a curve of constant width because no matter how
you turn it, the greatest distance across it is always the same.
However, the circle is not the only figure with this property.
Curves of Constant Width
11–2
Answers
(Lesson 11-2)
Geometry: Concepts and Applications
11–3
© Glencoe/McGraw-Hill
(24)
CD
A7
24
© Glencoe/McGraw-Hill
461
32
5. Suppose a chord of a circle
is 5 inches from the center
and is 24 inches long.
Find the length of the radius. 13 in.
Geometry: Concepts and Applications
6. Suppose the diameter of a circle is 30 centimeters long and a
chord is 24 centimeters long. Find the distance between the
chord and the center of the circle. 9 cm
4. Suppose a chord is 20 inches
long and is 24 inches from the
center of the circle. Find the
length of the radius. 26 in.
80
In each circle, O is the center. Find each measure.
២
2. KM
1. mNP
(OE)2 (ED)2 (OD)2
x2 122 152
x2 144 225
x2 81
x9
12
ED 1
2
1
2
Example: In the circle, O is the center, OD 15, and
CD 24. Find x.
• In a circle, a diameter bisects a chord and its arc if and
only if it is perpendicular to the chord.
• In a circle or in congruent circles, two minor arcs are
congruent if and only if their corresponding chords are
congruent.
?
?
?
苶E
T
苶
?
?
苶Q
E
苶
TE
SG
苶B
A
苶
TG
苶E
R
苶
GMS
EMT
?
12. If SR ⬵ AR, then R
苶G
苶⊥
苶A
S
苶
苶G
R
苶
?
?
?
14. If WY 38, then WZ 15. If WZ 15, then WY © Glencoe/McGraw-Hill
462
55
20. If mWY 110, then mWX ?
?
19. If BY 30 and BZ 18, then WY ?
?
?
30
19
23
18. If WY 40 and BZ 15, then WB 17. If WB 15 and BZ 9, then WZ 16. If BZ 6 and WZ 8, then WB ?
13. If BW 23, then BY 48
25
12
10
Use B, where B
苶X
苶 ⊥W
苶Y
苶, to complete each sentence.
?
11. If S
苶Q
苶⬵苶
EQ
苶, then T
苶M
苶⊥
10. If T
苶M
苶⊥苶
RG
苶 and ST ⬵ TE, then 䉭SQT ⬵ 䉭
?
?
8. If T
苶M
苶⊥苶
RG
苶, then ST ⬵
9. If T
苶M
苶⊥苶
RG
苶, then S
苶Q
苶⬵
?
7. If R
苶E
苶⬵苶
SG
苶, then RE ⬵
6. If RE ⬵ SG, then 䉭RME ⬵ 䉭
5. If R
苶G
苶⊥苶
AS
苶, then S
苶B
苶⬵
4. If ST ⬵ TE, 苶
ST
苶⬵
3. If T
苶M
苶⊥苶
RG
苶, then RT ⬵
2. If ST ⬵ ET, then 䉭SMT ⬵ 䉭
苶G
苶⬵
1. If SG ⬵ RE, then S
?
Skills Practice
NAME
Complete each sentence.
PERIOD
Arcs and Chords
3. XY
DATE
The following theorems state relationships between arcs,
chords, and diameters.
Study Guide
NAME
Arcs and Chords
11–3
W
R
X
A
B
S
Z
B
M
Q
T
Y
E
PERIOD
G
Geometry: Concepts and Applications
EQT
DATE
Answers
(Lesson 11-3)
Geometry: Concepts and Applications
© Glencoe/McGraw-Hill
72
A8
© Glencoe/McGraw-Hill
16
6. Find AB.
8 units
463
8
7. Find AB.
Geometry: Concepts and Applications
5. Suppose a radius of a circle is 17 units and a chord is 30 units
long. Find the distance from the center of the circle to the chord.
4. Find the length of a chord that is 5 inches from the center of a
circle with a radius of 13 inches. 24 in.
3. Suppose a chord of a circle is 16 inches long and is 6 inches from
the center of the circle. Find the length of a radius. 10 in.
12
DATE
Reading to Learn Mathematics
NAME
PERIOD
A
P
G
B
H
E
C
D
Z
W
C
Y
X
© Glencoe/McGraw-Hill
464
Geometry: Concepts and Applications
Sample answer: Since ⬔WCZ measures 90, all four angles measure
90. So, WXYZ is a rectangle. Since the angles are all congruent, the
minor arcs WX , XY, YZ , and WZ are all congruent. By Theorem 11-4,
if minor arcs are congruent, then their corresponding chords are
苶⬵苶
苶⬵苶
苶⬵苶
苶 and WXYZ is a
XY
YZ
WZ
congruent. That means that 苶
WX
rhombus. Because WXYZ is both a rectangle and a rhombus, it is
a square.
4. A good way to remember a mathematical concept
is to explain it in your own words. In the figure, 䉺C
contains quadrilateral WXYZ, where each vertex of
WXYZ lies on the circle. Explain why WXYZ is a square.
Helping You Remember
half of 40, or 20.
F
b. AG AG is half of AC, or 12, since the diameter is perpendicular to
the chord.
c. HE HE is PE PH. PE is the measure of a radius, which is half
of 40, or 20. So, HE 20 16, or 4.
d. FG FG is BF BG. 苶
B苶
F is a diameter which measures 40. BG is the
same as HE, or 4. So FG 40 4, or 36.
a. PA PA is the length of the radius, which is
3. In 䉺P, the diameter measures 40 and
AC FD 24. Find the measures in each
exercise. Explain how you find each
measure.
is perpendicular to the chord. In a circle, if a diameter is
perpendicular to a chord, then the diameter bisects the chord.
2. Refer to Theorem 11-5. Write an if-then statement and its converse using this
theorem. In a circle, if a diameter bisects a chord and its arc, then it
congruent, then the two corresponding minor arcs are congruent.
In the same circle or congruent circles, if two minor arcs are
congruent, then their corresponding chords are congruent.
1. Refer to Theorem 11-4. Write an if-then statement and its converse using this
theorem. In the same circle or congruent circles, if two chords are
Reading the Lesson
11–3
Arcs and Chords
PERIOD
In each figure, O is the center. Find each measure to the nearest
tenth.
1. YQ
2. mBC
Practice
DATE
Arcs and Chords
11–3
NAME
Answers
(Lesson 11-3)
Geometry: Concepts and Applications
DATE
PERIOD
11–4
Study Guide
NAME
DATE
17
A9
21
45
0
44 2
43 19
42 1
8
41
38 14
1
25
37
13
4
5
9
28
27
6
2 2
4
29
6 30
7 31
2
8 3
33
© Glencoe/McGraw-Hill
465
Geometry: Concepts and Applications
2. Copy the original circle, points, and numbers. Try other
patterns for connecting points. For example, you might try
tripling the first number to get the number for the second
endpoint of each chord. Keep special patterns for a possible
class display. See students’ work.
above. The pattern is a heart-shaped figure.
1. Use your ruler and pencil to draw chords to connect
numbered points as follows: 1 to 2, 2 to 4, 3 to 6, 4 to 8, and
so on. Keep doubling until you have gone all the way around
the circle. What kind of pattern do you get? For figure, see
48 2
Step B
Fold the circle
in half again.
Step C
Unfold the circle.
Step B
Fold another portion
in toward the center,
overlapping the first.
© Glencoe/McGraw-Hill
466
Geometry: Concepts and Applications
4. Cut out another circle and fold it to make a regular hexagon.
Draw the steps used.
5. Cut out a circle with radius 4 inches and fold it to make a
regular dodecagon. Draw the steps used.
Step D
Fold the four
arcs designated
by the creases.
PERIOD
Step C
Fold the remaining third
of the circle in toward
the center.
3. Cut out another circle and fold it to make a regular octagon.
Draw the steps used.
For Exercises 3-5, see students’ work.
Step A
Fold one portion in
toward the center.
See students’ work.
2. Draw another circle with a radius of 2 inches and cut it out.
Make the following folds to form a regular triangle.
Step A
Fold the circle
in half.
1. Draw a circle with a radius of 2 inches and cut it out. Make the
following folds to form a square. See students’ work.
You can make many regular polygons by folding a circular piece
of paper. The vertices of the polygon will lie on the circle, so the
polygon is said to be inscribed in the circle.
12 3
6
Inscribed Polygons
11
35
Some beautiful and interesting patterns result if you draw
chords to connect evenly spaced points on a circle. On the circle
shown below, 24 points have been marked to divide the circle
into 24 equal parts. Numbers from 1 to 48 have been placed
beside the points. Study the diagram to see exactly how this
was done.
Enrichment
NAME
22
34
Patterns from Chords
11–3
16
46
15
23
40
10
© Glencoe/McGraw-Hill
39
3
47
Answers
(Lessons 11-3 and 11-4)
Geometry: Concepts and Applications
© Glencoe/McGraw-Hill
10
2
4. WM 2x 5, ZN x 5
5. WM 5x 1, ZN 2x 5
A10
1
6
3
4
5
2
90
28.3 m
© Glencoe/McGraw-Hill
467
13. Find CA to the nearest tenth. 14.2 m
12. Find SQ to the nearest tenth.
11. Find m⬔SCQ.
S
P
C
A
O
WZ
Q
U
Q
N
PERIOD
Geometry: Concepts and Applications
R
M
DATE
Square SQUR is inscribed in C with a radius of 20 meters.
10. WM 20x 100, ZN 30x 80
9. WM x 1, ZN 2x 7
8. WM 4x, ZN 3x 1
7. WM x 8, ZN 2x 5
6. WM 4x 15, ZN 3x 19
6
3. WM x 6, ZN 2x 12
2. WM 3x 10, ZN 2x 15
1. WM x 8, ZN 2x 5
Use O to find x.
3
Skills Practice
NAME
Inscribed Polygons
11–4
Practice
NAME
DATE
5
2
6
x
© Glencoe/McGraw-Hill
9. AB 3x 7, CD 4x 21
2
14
8. AB 5(x 2), CD 10(x 1)
7. AB 3(x 1), CD 8x 13
4
6. AB 3(x 1), CD 2(x 5) 7
5. AB 2x 1, CD 3x 4
4. AB 4x 2, CD 2x 6
3. AB 3x 5, CD 2x 1
Use circle O to find x.
1. equilateral triangle
x
468
PERIOD
Geometry: Concepts and Applications
2. regular pentagon
Use a compass and straightedge to inscribe each polygon in a
circle. Explain each step. 1-2. See students’ work.
Inscribed Polygons
11–4
Answers
(Lesson 11-4)
Geometry: Concepts and Applications
© Glencoe/McGraw-Hill
PERIOD
A11
L
C
M
O
© Glencoe/McGraw-Hill
469
Geometry: Concepts and Applications
Sample answer: The inscribed polygon is inside the circle, so the
circumscribed polygon must be outside the circle.
3. Your friend has trouble remembering the difference between inscribed and
circumscribed polygons. What is an easy way to remember which is which?
Helping You Remember
苶.
First, Marian drew the circle and the diameter 苶
LO
Next, she constructed the perpendicular bisector of
苶O
苶, extending the line to intersect 䉺C at points M
L
P
and P. Finally, she connected the consecutive
points in order to form square MOPL. The sides of the square are
chords of the circle. The four chords are congruent because they are
equidistant from the center of the circle.
2. Marian constructed a regular quadrilateral,
or square, by inscribing it in a circle, as
shown in the diagram at the right. Describe
the steps that she took to consruct the square.
Then explain why the figure is a square.
order for it to be inscribed.
e. If two vertices of a polygon lie on a circle, then the polygon is an inscribed
polygon. False; every vertex of the polygon must lie on the circle in
d. If two chords are equidistant from the center of the circle, then the chords are
parallel. False; the chords are congruent.
some regular polygons can be constructed by inscribing them in
circles.
c. All regular polygons can be constructed by inscribing them in circles. False;
true
b. In a circle, two chords are congruent if they are equidistant from the center.
a. If every vertex of a polygon lies on the circle, then the polygon is a
circumscribed polygon. False; it is an inscribed polygon.
1. State whether each statement is true or false. If the statement is false,
explain why.
Reading the Lesson
inscribed polygon a polygon in which every vertex of the
polygon lies on the circle
Key Terms
DATE
Reading to Learn Mathematics
NAME
Inscribed Polygons
11–4
Enrichment
NAME
DATE
37.125 cm2
© Glencoe/McGraw-Hill
8. What is the area of the pentagon
to the nearest tenth of a
centimeter? 30.45 cm2
7. What is the perimeter of the
pentagon to the nearest tenth
of a centimeter? 21 cm
6. What is the measure of each of
the five congruent arcs? 72
5. Use a protractor to inscribe a regular
pentagon in 䉺P.
470
N
PERIOD
Geometry: Concepts and Applications
P
4.125 cm2
Make the appropriate changes in Steps 1–3 above to inscribe
a regular pentagon in P. Answer each of the following.
4. What is the area of the nonagon?
3. What is the area of one of the nine triangles formed?
2. Measure the distance from the center perpendicular to one of
the sides of the nonagon. 3.3 cm
1. Find the length of one side of the
nonagon to the nearest tenth of a
centimeter. What is the perimeter of
the nonagon? 2.5 cm, P 22.5 cm
Step 3: Connect the nine points to form the
nonagon.
Step 2: Draw 9 radii to form 9 angles with
the measure you found in Step 1.
The radii will intersect the circle in
9 points.
Step 1: Find the degree measure of each of
the nine congruent arcs. 40
A protractor can be used to inscribe a regular polygon in a circle.
Follow the steps below to inscribe a regular nonagon in N.
Area of Inscribed Polygons
11–4
Answers
(Lesson 11-4)
Geometry: Concepts and Applications
Study Guide
NAME
© Glencoe/McGraw-Hill
diameter d
A12
C 44 ft
5
2.
© Glencoe/McGraw-Hill
8
6. What is the circumference of the top
of an ice cream cone if its diameter is
7
about 1 inches? C 6 in.
Solve. Round to the nearest inch.
471
C 50 in.
4. The radius is 6 1 feet. C 39 m
1.
Find the circumference of each circle.
C d
C (6)
C ⬇ 18.85
C ⬇ 19 cm
radius r
3.
DATE
C 28 m
C 2r
C 2(5)
C 10
C ⬇ 31.4
C ⬇ 31 m
circumference C
distance
around a
circle
PERIOD
Geometry: Concepts and Applications
C 57 in.
7. The radius of the basketball rim is
9 inches. What is the circumference?
5. The diameter is 4.7 yards. C 15 yd
Examples: Find the circumference of each circle.
center
Circumference of a Circle
11–5
Skills Practice
NAME
62.8 ft
5. circular garden with
radius 10 feet
50.3 ft
2. a circular top of a
trampoline with
diameter 16 feet
119.4 m
17. r 19 m
219.9 ft
14. d 70 ft
1256.6 ft
11. r 200 ft
62.8 yd
8. d 20 yd
110.0 yd
18. d 35 yd
18.8 in.
15. r 3 in.
15.7 in.
12. d 5 in.
6.3 m
9. r 1 m
12.6 ft
6. circular mirror with
diameter 4 feet
9.4 cm
© Glencoe/McGraw-Hill
11.9 yd
25. 75 yd
4.5 cm
22. 28 cm
15.9 m
19. 100 m
472
2.2 cm
26. 14 cm
12.7 in.
23. 80 in.
5.1 ft
20. 32 ft
Geometry: Concepts and Applications
39.8 ft
27. 250 ft
4.0 m
24. 25 m
2.9 mi
21. 18 mi
Find the radius of each circle to the nearest tenth for each circumference given.
31.4 in.
16. d 10 in.
12.6 m
13. r 2 m
18.8 ft
10. d 6 ft
44.0 cm
7. r 7 cm
Find the circumference of each circle to the nearest tenth.
34.6 cm
4. a CD with diameter
11 centimeters
75.4 ft
1. a round swimming pool
with radius 12 feet
PERIOD
3. the circular base of a
paper weight with
diameter 3 centimeters
DATE
Find the circumference of each object to the nearest tenth.
Circumference of a Circle
11–5
Answers
(Lesson 11-5)
Geometry: Concepts and Applications
Practice
NAME
DATE
© Glencoe/McGraw-Hill
37.7 cm
213.6 mm
18.8 cm
A13
5兹2
苶 in.
14 in.
© Glencoe/McGraw-Hill
9.
7.
473
Find the exact circumference of each circle.
5. 6 cm
3. 34 mm
1. 3 cm
10.
8.
PERIOD
Geometry: Concepts and Applications
8 cm
16 cm
26 cm
31.4 miles
28.3 m
12.6 ft
6. 5 miles
4. 4.5 m
2. 2 ft
Find the circumference of a circle with a radius of the given
length. Round your answers to the nearest tenth.
Circumference of a Circle
11–5
PERIOD
© Glencoe/McGraw-Hill
474
Geometry: Concepts and Applications
polygon and the circumference of a polygon are similar in that they
are both the distance around a figure. They are different in that the
perimeter of a polygon involves measuring segments, while the
circumference of a circle is curved. The formula for perimeter of a
polygon uses addition of the lengths of the segments that are sides.
The formula for the circumference of a circle involves multiplying
the diameter by .
3. Write several sentences explaining the similarities and differences between the
perimeter of a polygon and the circumference of a circle. Be sure to mention the
formulas used to find these measures. Sample answer: The perimeter of a
Helping You Remember
circumference and solve for r. So, C = 2r, 163.4 = 2r, 81.7 r,
r 81.7 or about 26 centimeters.
c. Find the radius of a circle with a circumference of approximately 163.4
centimeters. Use the formula C 2r. Substitue 163.4 for the
C 2r, since the radius is given. The circumference is 2 • • 6,
which is approximately 37.7 feet.
b. Find the circumference of a circle with a diameter of 15 inches. Use the
formula C d, since the diameter is given. The circumference is
15, which is approximately 47.1 inches.
a. Find the circumference of a circle with a radius of 6 feet. Use the formula
2. For the following exercises, use the given information to find the required
measure. Round the measure to the nearest tenth. Show how you find the
measure.
False; the ratio of the circumference to the diameter is pi.
c. The distance around a circle is called the circumference. true
d. By definition, the ratio of the circumference of a circle to the radius is pi.
b. If you know the diameter of a circle, you can find the circumference by using
the formula C 2d. False; the formula is C d.
a. The number is an irrational number. true
1. State whether each statement is true or false. If the statement is false,
explain why.
Reading the Lesson
circumference (sir•KUM•fur•ents) the distance around a circle
pi () a Greek letter that represents the ratio of the
circumference of a circle to its diameter
Key Terms
DATE
Reading to Learn Mathematics
NAME
Circumference of a Circle
11–5
Answers
(Lesson 11-5)
Geometry: Concepts and Applications
35.8 m
11–6
Study Guide
NAME
DATE
© Glencoe/McGraw-Hill
A14
9 yd
24 in.
29 cm
34 mm
14 yd
5 mm
12 yd
15 yd
18 mm
© Glencoe/McGraw-Hill
9.
7.
5.
3.
1.
266.9 mm
78.82 yd
113.04 in.
83.12 cm
8 cm
51.7 m
475
10.
8.
6.
4.
2.
92.1 m
7.7 m
9 ft
6 ft
12 m
94.2 ft
37.68 m
6.4 m
153.86 ft
Geometry: Concepts and Applications
24.5 ft
18.5 m
24 m
A r2
A (6)2
A ⬇ 113.10
A r2
A (20)2
A ⬇ 1256.64
153.9 ft2
2.
38.5 mm2
603.2 in2
© Glencoe/McGraw-Hill
4.
5.
476
685.8 cm2
Find the area of each shaded region to the nearest tenth.
1.
1,284.8 m2
176.7 yd2
PERIOD
Geometry: Concepts and Applications
6.
3.
Now find the area of the shaded region.
A ⬇ 1256.64 3(113.10)
⬇ 1256.64 339.3
⬇ 917.34
The area of the shaded region is about 917.3 m2.
Find the area of
a small circle.
Find the area of
the large circle.
Assume that the smaller circles are congruent.
2 Find the area of the shaded region.
A (42.25)
A ⬇ 132.73
The area of the circle is about 132.7 in2.
2
A r2
2
A 冢13 冣
1 Find the area of the circle.
Find the area of each circle to the nearest tenth.
Examples
The area A of a circle equals times the radius r squared: A r2.
77.045 m
PERIOD
Area of a Circle
DATE
Use a calculator to find the perimeter (the solid lines and
curves) of each figure. Use ␲ 3.14.
Enrichment
NAME
Finding Perimeter
11–5
Answers
(Lessons 11-5 and 11-6)
Geometry: Concepts and Applications
11–6
Practice
NAME
DATE
© Glencoe/McGraw-Hill
A15
113.10 in2
14. r 6 in.
6361.73 m2
11. d 90 m
1385.51 m2
8. C 131.95 m
28.27 in2
5. d 6 in.
1017.88 cm2
2. r 18 cm
1809.64 m2
15. C 150.80 m
31,416.07 ft2
12. C 628.32 ft
4300.92 ft2
9. C 232.48 ft
706.86 m2
6. d 30 m
2
© Glencoe/McGraw-Hill
87.27 in
22. 100°
39.27 in2
19. 45°
78.54 in2
16. 90°
2
477
130.90 in
23. 150°
52.36 in2
20. 60°
26.18 in2
17. 30°
2
Geometry: Concepts and Applications
61.09 in
24. 70°
117.81 in2
21. 135°
104.72 in2
18. 120°
A circle has a radius of 10 inches. Find the area of a sector whose central angle has
the following measure. Round to the nearest hundredth.
70,685.83 ft2
13. d 300 ft
3.14 mi2
10. r 1 mi
78.56 yd2
7. C 31.42 yd
1963.50 ft2
4. d 50 ft
314.16 in2
1. r 10 in.
19.22 in2
8. C 15.54 in.
5.59
mi2
3
ft2
5. d 22 mi
38.48
2
2. r 31 ft
© Glencoe/McGraw-Hill
2.62 cm2
11. 12
2.18 cm2
8. 10
478
26.18 cm2
12. 120
39.27 cm2
9. 180
PERIOD
2
Geometry: Concepts and Applications
9.82 cm2
13. 45
7.85 cm2
10. 36
12.43 mi2
9. C 121 mi
32.37 in2
6. d 6.42 in.
16.62 mm2
3. r 2.3 mm
In a circle with radius of 5 cm, find the area of a sector whose
central angle has the following measure. Round to the nearest
hundredth.
509.30 mm2
7. C 80 mm
132.73
ft2
4. d 13 ft
28.27
cm2
1. r 3 cm
Find the area of each circle described. Round your answers to the
nearest hundredth.
50.27 mm2
PERIOD
Find the area of each circle to the nearest hundredth.
3. r 4 mm
DATE
Area of a Circle
Skills Practice
NAME
Area of a Circle
11–6
Answers
(Lesson 11-6)
Geometry: Concepts and Applications
© Glencoe/McGraw-Hill
PERIOD
2
A16
O 135°
© Glencoe/McGraw-Hill
479
Geometry: Concepts and Applications
answer: Circumference is measured in linear units, while area is
square units, so the formula containing r2 must be the one for area.
4. A good way to remember something is to explain it to someone else. Suppose your
classmate Adrienne is having trouble remembering which formula is for
circumference and which is for area of a circle. How can you help her? Sample
Helping You Remember
10 m
By Theorem 11-9, the area of a sector is
N
A (r2). Substituting the values from the diagram,
360
135
3
A ()(10)2. Simplifying, A • 100.
360
8
Using a calculator and rounding, A ⬇ 117.8 square meters.
3. Find the area of the shaded region in 䉺O to
the nearest hundredth. Explain your
method for finding the area.
To find the area, first use the value of the circumference to find
the radius. Then use the radius to find the area. By Theorem 11-7,
C 2r. Substitute the value for circumference to form an equation
to get 36 2r. Solve for r to get r 18. By Theorem 11-8, A r2.
Substitute the value for r to find the area, A (18)2. Use a calculator
and round the answer, A ⬇ 1017.9 square feet.
2. Suppose 䉺A has a circumference of 36 feet. Find the area of the circle to the
nearest tenth. Explain how you find the area and justify the steps you take.
sector of a circle is a region bounded by a central angle and its
e. A(n) __________
corresponding arc.
360 .
d. The sum of the measures of the central angles of a circle is _____
r .
c. If a circle has an area of A square units and a radius of r units, then A _____
b. The area of a geometric figure, such as a circle, is always expressed in
square units.
___________
N
(r2)
a. If a sector of a circle has an area of A square units, a central
360
angle measurement of N degrees, and radius of r units then A __________
.
1. Complete each sentence.
Reading the Lesson
sector a region of a circle bounded by a central angle and its
corresponding arc
Key Terms
DATE
Reading to Learn Mathematics
NAME
Area of a Circle
11–6
Enrichment
NAME
DATE
© Glencoe/McGraw-Hill
12 ft
3. Rover’s chain is attached to the
corner of the house.
area 108 ft2
12 ft
1. Rover’s chain is attached to a
stake in the middle of the yard.
area 144 ft2
480
PERIOD
18 ft
12 ft
4 ft
Geometry: Concepts and Applications
8 ft
4. Rover’s chain is attached to a
4-foot by 18-foot rectangular shed.
area 124 ft2
12 ft
2. Rover’s chain is attached to a
long wall.
area 72 ft2
Robin is going to fix a chain to tie up his dog Rover. There are
several places in the yard that Robin can attach the end of the
chain. For each of the following, use a compass to draw the
space that Rover can reach while on the end of a 12-foot chain.
Then find the area.
Area of Circular Regions
11–6
Answers
(Lesson 11-6)
Geometry: Concepts and Applications
Chapter 11 Answer Key
Form 1A
Page 481
Page 482
1.
2.
B
11.
B
12.
C
2.
C
5.
C
7.
8.
B
3.
14.
B
15.
D
16.
D
17.
B
18.
A
10.
A
19.
D
20.
B
© Glencoe/McGraw-Hill
B
13.
A
14.
C
15.
D
16.
C
17.
B
18.
B
19.
C
20.
C
A
Bonus
D
A17
A
5.
D
8.
Bonus
12.
D
B
7.
A
D
B
C
4.
6.
D
9.
11.
A
B
4.
6.
1.
A
13.
3.
Form 1B
Page 483
Page 484
D
B
C
9.
B
10.
C
Geometry: Concepts and Applications
Chapter 11 Answer Key
Form 2A
Page 485
1.
U
S
and T
V
2.
6
4
Page 486
3
13.
7
14.
7
in.
4
15.
35 ft
16.
48
17.
7238 cm2
18.
286.5 mm2
19.
140 ft2
20.
32%
1
3.
10
4.
mED 42;
mEA 138;
mEC 144
5.
false; major
6.
78
7.
minor arc; 360
8.
EGD
9.
9
4
10.
32
3
11.
25 cm
12.
chord; radius
© Glencoe/McGraw-Hill
Bonus
A18
6.6 m
Geometry: Concepts and Applications
Chapter 11 Answer Key
Form 2B
Page 487
1.
C
A
2.
7.1
Page 488
13.
5
14.
4.0 ft
3.
7
15.
24 m
16.
471 ft
4.
mMNL 260;
mMLP 250;
mMLN 280
17.
201 mm2
6.
false;
semicircle
100
18.
78.5 m2
7.
central angle
EF
19 yd2
8.
19.
9.
13
10.
10
20.
79%
11.
50 cm
Bonus
8 cm
5.
12. false; vertices, on
© Glencoe/McGraw-Hill
A19
Geometry: Concepts and Applications
Chapter 11 Assessment Answer Key
Page 489, Extended Response Assessment
Scoring Rubric
Score
General Description
Specific Criteria
4
Superior
A correct solution that
is supported by welldeveloped, accurate
explanations
•
Satisfactory
A generally correct solution,
but may contain minor flaws
in reasoning or computation
•
Nearly Satisfactory
A partially correct
interpretation and/or
solution to the problem
•
Nearly Unsatisfactory
A correct solution with no
supporting evidence or
explanation
•
•
Unsatisfactory
An incorrect solution
indicating no mathematical
understanding of the
concept or task, or no
solution is given
•
3
2
1
0
© Glencoe/McGraw-Hill
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Shows thorough understanding of the concepts of circles,
constructions, congruence, area, angle measure, and sectors and
segments of circles.
Uses appropriate strategies to solve problems.
Computations are correct.
Written explanations are exemplary.
Graphs are accurate and appropriate.
Goes beyond requirements of some or all problems.
Shows an understanding of the concepts of circles, constructions,
congruence, area, angle measure, and sectors and segments of
circles.
Uses appropriate strategies to solve problems.
Computations are mostly correct.
Written explanations are effective.
Graphs are mostly accurate and appropriate.
Satisfies all requirements of problems.
Shows an understanding of most of the concepts of circles,
constructions, congruence, area, angle measure, and sectors and
segments of circles.
May not use appropriate strategies to solve problems.
Computations are mostly correct.
Written explanations are satisfactory.
Graphs are mostly accurate.
Satisfies the requirements of most of the problems.
Final computation is correct.
No written explanations or work is shown to substantiate
the final computation.
Graphs may be accurate but lack detail or explanation.
Satisfies minimal requirements of some of the problems.
Shows little or no understanding of the concepts of circles,
constructions, congruence, area, angle measure, and sectors and
segments of circles.
Does not use appropriate strategies to solve problems.
Computations are incorrect.
Written explanations are unsatisfactory.
Graphs are inaccurate or inappropriate.
Does not satisfy requirements of problems.
No answer may be given.
A20
Geometry: Concepts and Applications
Chapter 11 Answer Key
Extended Response Assessment
Sample Answers
Page 489
1. 14 cm
4. Answers to parts a–h depend on the
precision of students’ drawings and
measurements.
2.
C
A
Q
C
P
B
M
Q
A
P
B
M
D
D
3.
a. AM 4.7 cm, BM 9.3 cm,
CD 7.4 cm
C
b. 17.39 cm2
A
Q
P
B
c. 34.41 cm2
M
d. 77; 24.19 cm2
D
e. 44; 38.40 cm2
f. 6.80 cm2
g. 3.99 cm2
a. Yes; SSS Postulate (congruence)
h. 10.79 cm2
b. Yes; CPCTC
c. 90
© Glencoe/McGraw-Hill
A21
Geometry: Concepts and Applications
Chapter 11 Answer Key
Mid-Chapter Test
Page 490
Quiz A
Page 491
1.
3.
true
false
false
4.
3.9
1.
2.
2.
3.
4.
5.
6.
46.5
5.
7.
8.
8.
138
218
180
9.
false; 360 6.
7.
10.
11.
5.7
13.
15
14.
41 in.
© Glencoe/McGraw-Hill
chord
1
12 2
122
mBFC 360 mBAC
207
111
180
Quiz B
Page 491
1.
9.2
2.
5
3.
8
4.
69.1 ft
5.
117.3 m2
ADE or AED
13
12.
B
A
, A
C
, AF
A22
Geometry: Concepts and Applications
Chapter 11 Answer Key
Cumulative Review
Page 492
1.
Standardized Test Practice
Page 493
Page 494
false;
1.
2.
y2
3.
57; acute
4.
38
5.
right, scalene
6.
33
7.
T, R, S
8.
100
9.
8
10.
90 ft
11.
61.2 mm
12.
696
ft2
13.
68 m
14.
44.0 in.
© Glencoe/McGraw-Hill
A23
D
12.
A
13.
D
14.
C
15.
A
16.
B
17.
C
18.
A
19.
C
20.
D
B
2.
A
3.
A
4.
C
5.
D
6.
B
7.
C
8.
C
9.
D
10.
11.
D
Geometry: Concepts and Applications