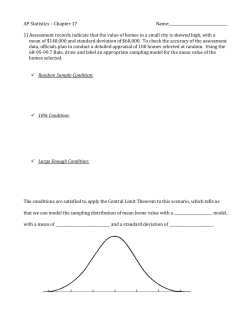
Chapter 5 Notes
Section 5.2 Expected Values, Standard Deviations and Probability
Suppose the students in a math class are asked to toss a fair coin 100 times each and record the
number of times heads comes up. Will each student in the class observe the same number of
heads? How much will this number vary? What do you think the average number of heads will
be for all students?
Terminology
A discrete random variable, X, is a an assignment of a number to each of the outcomes
in the sample space
The probability density function (pdf), Pr(X), is the formula/table that assigns a
probability to each element (or, each value of x) in the domain/sample space.
Properties of a Probability Density Function
If X is a discrete random variable, then X has the following properties…
1.
0 Pr(X) 1 for all x in the domain
Pr( X ) 1
2.
all x
Ex.
Roll a die…Let X = the square of the number of dots facing up
Outcome
X
Pr(X)
Expected Value, Variance and Standard Deviations of a Random Variable
The mean/expected value, , of a discrete random variable is
E ( X ) x Pr( x )
all x
The variance, , the measure of dispersion of the distribution of a random variable, is
2
Var ( X ) 2
(x )
2
p( x)
all x
The Standard Deviation is simply the square root of the variance is
StDev( X )
(x )
2
p ( x)
all x
1
Ex.
Roll a die…Let X = the square of the number of dots facing up. Find the mean, or
expected value of the random variable. What does this mean?
Outcome
X
Pr(X)
Ex.
A random variable, X, and its probability density function are shown below. What are
the missing entries?
Ex.
If the experiment is a series of Bernoulli trials, then the random variable, X, is the
number of successes and is called a binomial random variable
Let X = numbers of successes in a sequence of 3 Bernoulli trials where the probability of
success is 0.6
Find the mean of the random variable
X
Pr(X)
2
Ex.
Ex.
A random variable, X, has the given probability density function. Find the mean,
variance and standard deviation.
X
Pr(x)
-2
0.45
-1
0.4
1
0.1
4
0.05
∙ Pr
∙ Pr
In the game roulette, there are 38 numbered positions on the wheel. 18 are red, 18 are
black, and 2 are green. A $5 bet is placed on red. If the ball lands on red, the player will
receive $10 (the original $5 plus $5 in winnings). If not, the player will receive $0 (the
original $5 plus a winnings of -$5). Find the expected value of the roulette game when a
player bets red.
Let X = amount won. Then the probability distribution looks like this…
outcome
X
P(X)
win
lose
The expected value of the game is…
lose
!
. Every time you bet on red, you expect to
3
Ex.
A state lottery ticket costs $1. The probability of winning $10,000 is 0.00001, the
probability of winning $100 is 0.005, and the probability of winning $10 is 0.02. Find the
expected value (gain or loss) on one ticket.
X
Ex.
Pr(x)
∙ Pr
Two coins are selected at random from an urn containing 1 quarter, 3 dimes, and 1 nickel.
A random variable is defined as the value of the coins (in cents). Find the probability
density function, expected value, and the standard deviation.
4
Special Cases:
If X is a binomial random variable, then…
1
.
1
Ex.
An unfair coin, where the probability of heads is 0.55 is flipped 200 times. Let X
represent the number of times heads comes up in the 200 flips. Find E(X), Var(X), and
St.Dev(X)
Ex.
A fair die is rolled 500 times. Let X represent the number of times a 3 is rolled.
Find ,
, and Ex.
The probability that a woman is widowed or divorced is 80%. Ten women are
interviewed at random. Let the random variable X be defined as the number of women
who are widowed or divorced. Find the expected value and standard deviation.
5
Section 5.3 The Normal Distribution
Discrete vs Continuous Random Variables
Some random variables are discrete while others are continuous.
A discrete random variable can assume a countable number of values.
Ex. The number of customers standing in line to see a bank teller: X = {0, 1, 2, 3…}
A continuous random variable can assume any value along a given interval of
a number line.
|
Ex. The length of time a customer waits in line to see a bank teller:
0
Normal Random Variable
What is a normal distribution and why is it important?
It is a mound (bell)-shaped distribution.
Reasonably approximates distributions of many variables.
Very important distribution in inferential statistics
Characteristics of the Normal Distribution
Shape is defined by two parameters, and
The mean, , is the center and represent the line of symmetry. The standard deviation,
, determines the spread.
The curve drops smoothly on both sides, flattening near but never touching the x-axis.
The points of inflection (curve changes from concave down to concave up) occur one
standard deviation on either side of the mean and enclose about 2/3 of the total area.
.
6
The Standard Normal Distribution (aka the "Z-Distribution")
It is a normal distribution with
0 and
1
The corresponding curve is called the standard normal curve.
The letter Z is often used to represent a variable whose distribution is described by the
standard normal curve.
Finding Standard Normal Probabilities
To find the probability of a normal random variable, say
, it is necessary to
calculate the area under the standard normal curve between a and b.
We will use the standard normal probability tables to calculate these probabilities.
Area under the Standard Normal Curve (aka the “Z-Curve”)
Case 1: finding area/probability to the left of z: Pr
Pr
0.43
Pr
2
Pr
1.35
7
Case 2: finding area/probability to the right of z: Pr
Pr
1.96
Pr
0.83
Case 3 finding area/probability between a and b: Pr
Pr 2.00
2.00
Pr 1.03
2.41
What is a z-score?
The standard score, or z-score, is the number of standard deviations a random variable
falls from the mean.
Any value in a normal distribution can be converted to a z-score
z
x
The sign of any Z-score indicates the direction of a score: whether that observation fell
above the mean (the positive direction) or below the mean (the negative direction)
8
Ex.
Suppose X is normally distributed with mean = 15 and standard deviation = 3. Find
a.
Ex.
P(X 13)
b.
P(13 X 19)
Suppose X is normally distributed with mean = 1.3 and standard deviation = 0.2.
Find
a.
P(X ≥ 1)
b.
P(0.5 X 1.5)
Applications where normal probability is often used.
Defining a random variable to be normal is often appropriate when measuring height, weight,
IQ's, temperature, and many other test scores, along with many other situations
Ex.
Adult male heights are a normal random variable with mean 5 ft 10 inches and a
standard deviation of 3 inches. Find the percent of adult males taller than 6 ft 4 inches.
Ex.
On a recent test, student test scores were normally distributed with a mean of 74 and
standard deviation of 13. What percent of students failed the test?
Ex.
Adult IQs are normally distributed with mean 100 and standard deviation 15. Find the
probability that an adult’s IQ is between 85 and 115.
9
Using the Normal Table in Reverse
Ex. Find the value of z* in the standard normal tables such that the area to the left of z* is
approximately 60%
Ex.
Find the value of z* in the standard normal tables such that the area to the right of z* is
approximately 20%
Finding Percentiles
The kth percentile of a normal distribution with mean and standard deviation is the
∗
value, x*, for which Pr
0.01 (in other words, the area to the left of x* is 0.01k)
Note :If
, then
Ex.
Adult IQs are normally distributed with mean 100 and standard deviation 15. Find the
95th percentile for adult IQ scores
Ex.
On a recent test, student test scores were normally distributed with a mean of 74 and
standard deviation of 13. If the teacher says she will give A's to students whose scores
are in the top 10 percent, what is the minimum score needed to get an A?
10
© Copyright 2026