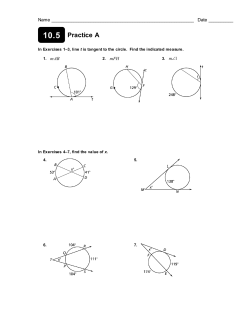
DO NOT EDIT--Changes must be made through "File info"
CorrectionKey=NL-A;CA-A
Name
Class
Date
16.3 Sector Area
Essential Question: How do you find the area of a sector of a circle?
Resource
Locker
Explore
Derive the Formula for the Area of a Sector
A sector of a circle is a region bounded by two radii and their intercepted arc.
A sector is named by the endpoints of the arc and the center of the circle. For
example, the figure shows sector POQ.
In the same way that you used proportional reasoning to find the length of an
arc, you can use proportional reasoning to find the area of a sector.
P
sector
O
Find the area of sector AOB. Express your answer in terms of π and rounded to
the nearest tenth.
A
First find the area of the circle.
A = πr 2 = π(
=
225π
A
15 mm
15 )2
Q
O 120°
B
B
120
The entire circle is 360°, but ∠AOB measures 120°. Therefore, the sector’s area is ___
or __13 of
360
the circle’s area.
Area of sector AOB = __1 · 225π
The area is __1 of the circle’s area.
3
© Houghton Mifflin Harcourt Publishing Company
=
=
3
75π
Simplify.
235.6
So, the area of sector AOB is
Use a calculator to evaluate. Then round.
75π mm 2
or
235.6 mm 2 .
Reflect
1.
How could you use the above process to find the area of a sector of the circle whose central angle
measures m°?
5m
m
m
of the circle’s area, or ___
∙ 225π. This can be written as ___
π.
The area of the sector is ___
360
360
8
2.
Make a Conjecture What do you think is the formula for the area of a sector with a central angle
of m° and radius r?
m
· πr 2
A = ____
360
Module 16
GE_MNLESE385801_U6M16L3.indd 873
873
Lesson 3
02/04/14 12:20 PM
DO NOT EDIT--Changes must be made through "File info"
CorrectionKey=NL-A;CA-A
DO NOT
Correcti
Using the Formula for the Area of a Sector
Explain 1
The proportional reasoning process you used in the Explore can be generalized. Given a sector with a
m
central angle of m° and radius r, the area of the entire circle is πr 2 and the area of the sector is___
times
360
the circle’s area. This give the following formula.
Area of a Sector
The area A of a sector with a central angle of m° of a circle with radius r is given by
m
A = ___
· 225π 2
360
Example 1 Find the area of each sector, as a multiple of
nearest hundredth.

sector POQ
_
A = m · πr 2
360
P
210· π(3) 2
=_
360
7 · 9π
=_
12
O 210°
3 in.
28 π
=_
3
≈ 29.32 in2
Q

π and to the
sector HGJ
J
12 m
G 131°
m · πr 2
A = ___
360
=
1
___
10
12
)
2
· 144 π
= 52.4 π
≈ 164.62 m 2
Reflect
3.
Discussion Your friend said that the value of m° in the formula for the area of a sector can never be larger
than 360°. Do you agree or disagree? Explain your reasoning.
Agree; a complete revolution is 360°, so a sector which is a part of a circle will always have
an central angle that is less than 360°.
Module16
GE_MNLESE385801_U6M16L3.indd 874
874
© Houghton Mifflin Harcourt Publishing Company
H
(
131
=_· π
360
Lesson3
23/03/14 8:42 AM
DO NOT EDIT--Changes must be made through "File info"
CorrectionKey=NL-A;CA-A
Your Turn
Find the area of each sector, as a multiple of π and to the nearest hundredth.
4.
sector AOB
5.
sector POQ
P
Q
24 mm
1.6 cm
A
O
B
O
m
_
· πr
360
22.5
= _ · π(24)
360
1
_
· 576π
=
A=
∠AOB is a straight angle,
so m° = 180°, r = 0.8 cm
m
_
· πr
360
180
= _ · π(0.8)
A=
22.5°
2
2
2
16
= 36π
2
360
1 (
__
= 2 · 0.64)π
≈ 113.10mm 2
= 0.32π
≈ 1.01cm 2
Applying the Formula for the Area of a Sector
Explain 2
You can apply the formula for the area of a sector to real-world problems.
© Houghton Mifflin Harcourt Publishing Company • Image Credits: ©Narvikk/
Vetta/Getty Images
Example 2 A beam from a lighthouse is visible for a
distance of 3 mi. To the nearest square mile,
what is the area covered by the beam as it
sweeps in an arc of 150°?
m · πr 2
A=_
360
150· π(3) 2
=_
360
5 · 9π
=_
12
= 3.75π
≈ 12mi 2
 A circular plot with a 180 foot diameter is watered by a spray irrigation system. To the nearest
square foot, what is the area that is watered as the sprinkler rotates through an angle of 50°?
d = 180 ft, so r = 100 ft
m · πr 2
A=_
360
(
50
= _ · π 90
360
=
Module16
GE_MNLESE385801_U6M16L3.indd 875
5
___
36
·
)
2
8100 π
=
1125 π
=
3,535
ft 2
875
Lesson3
23/03/14 8:42 AM