1. No category

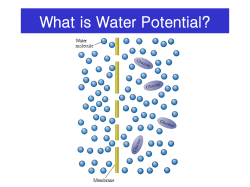
Calculating Molality - I
To calculate Molality (mol/kg), we need the number of moles of
solute, and the mass of solvent used to dissolve the solute!
Normally, we are given the mass of solute, and mass of solvent,
therefore we calculate the moles of the solute from the mass, then
use the mass of the solvent to calculate the molality.
Remember:
Molality is different from Molarity
Mass (g) of solute
M (g/mole)
Molality is based on mass, and is
independent of temperature or
pressure (unlike molarity)
Because 1 L of H2O weighs 1 kg,
molality and molarity of dilute
aquous solutions are nearly identical
Moles of Solute
divide by kg water
Molality (m) of solution
1
Calculating Molality - II
Problem: Determine the molality and molarity of a solution prepared
by dissolving 75.0g Ba(NO3)2 (s) in to 374.00g of water at 250C.
Plan: We convert the quantity of Ba(NO3)2 to moles using the molar
mass and then divide by the volume of H2O in liters (using water
density = 0.99707 g/ml3).
Solution: molar mass of Ba(NO3)2 = 261.32 g/mol
75.0 g
moles Ba(NO3)2 =
= 0.28700 mole
261.32 g/mol
molality = 0.28700 mole = 0.76739 m = 0.767 m
0.37400 kg
molarity - we need the volume of solution, and can assume that
addition of the salt did not change the total volume.
374.00 g H2O = 375.099 ml = 0.375099 l
0.99707 g/ml
M = 0.28700 mole = 0.765 M
0.375099 l
Expressing Concentrations in Parts by Mass
Problem: Calculate the PPB by mass of Iron in a 1.85 g Iron
supplement pill that contains 0.0543 µg of Iron.
Plan: Convert µg Fe to grams and then use Fe/ mass pill and
multiply by 109 to obtain PPB.
Solution: 0.0543µg Fe = 5.43 x 10 - 8 g Fe
5.43 x 10 - 8 g Fe x 109
= 2.94 PPB
1.85 g
2
Expressing Concentrations in Parts by Volume
Problem: The label on a can of beer (340 ml) indicates “4.5% alcohol
by volume”. What is the volume in liters of alcohol it contains?
Plan: we know the vol% and the total volume so we use the definition
to find the volume of alcohol.
Solution:
Vol Alcohol = 4.5 ml alcohol x 340 ml beer
100 ml beer
= 15.3 ml alcohol
Expressing Concentrations in Mole Fraction
Problem: A sample of alcohol contains 118g of ethanol (C2H5OH), and
375.0g of water. What are the mole fractions of each?
Plan: we know the mass and formula of each compound so we convert
both to moles and apply the definition of mole fraction.
Solution:
Moles Ethanol = 118g Ethanol = 2.744 mol Ethanol
43g Ethanol/mol
Moles Water =
395g H2O = 21.94 mol H O
2
18g H2O/mol
XEthanol =
XWater =
2.744
= 0.11117
21.94 +2.744
21.94
21.94 +2.744
= 0.88883
3
Converting Concentration Units
Problem: Commercial concentrated Hydrochloric acid is 11.8 M HCl
and has a density of 1.190g/ml. Calculate the (a) mass% HCl,
(b) molality and (c) mole fraction of HCl.
Plan: We know Molarity and density. (a) For mass% HCl we need the
mass of HCl and water (the solvent). Assume 1L of solution, from
the density we know the mass of the solution, and from the
molecular mass of HCl we calculate its mass. (b) We know moles
of HCl and mass of water (c) we use moles HCl from(a) and use
the mass of water to get moles of water then calculate mole
fractions and add them to check!
Solution:
(a) assume 1L of HCl solution
11.8 moles HCl x
36.46g HCl
mole HCl
11.8 moles HCl
= 430.228g HCl
Converting Concentration Units - II
(a) cont.
1L solution x 1000 mL x 1.190 g soln = 1190g solution
1 L solution
mL soln
mass % HCl = 430.228 g HCl x 100% = 36.1536 % HCl
1190.g solution
(b)
mass of H2O = mass of solution - mass of HCl =
1190g solution - 430.228g HCl = 759.772g H2O
1190g solution
11.8 moles HCl = 15.53 m HCl
0.759772 kg H2O
(c)
759.772g H2O
= 42.172 mole H2O
18.016g H2O/mol H2O
XHCl = 11.8 = 0.219
54.0
XH2O =42.172 = 0.781
54.0
Total moles =
42.172 + 11.8
= 53.972=54.0
4
Definitions
Saturated - A solution containing the maximum amount of solute that
will dissolve under a given set of conditions.
Unsaturated - A solution that contains less than the saturation quantity
of solute. More solute may be added and it will dissolve.
Supersaturated - A solution prepared at an elevated temperature and
then slowly cooled so that more than the usual
maximum amount of solute remains dissolved.
Equilibrium in a Saturated Solution
5
For all gasses: ∆Hsolute ≈ 0, so ∆Hsoln < 0
Gas solubility always decreases with increasing T!
The Effect of Pressure on Gas Solubility:
Henry’s Law: Sgas = kH x Pgas
6
Henry’s Law of Gas Solubility
Problem: The lowest level of oxygen gas dissolved in water that will
support life is ~ 1.3 x10-4 mol/L. At the normal atmospheric pressure of
oxygen is there adequate oxygen to support life in water?
Plan: We will use Henry’s law and the Henry’s law constant for oxygen
in water with the partial pressure of O2 in the air to calculate the amount
of O2 dissolved in water under atmospheric conditions.
Solution:
The Henry’s law constant for oxygen in water is 1.3 x 10 -3 mol
liter atm
and the partial pressure of oxygen gas in the atmosphere is ~21%,
or 0.21 atm.
Soxygen = kH x PO2 = 1.3 x 10 -3 mol x (0.21 atm)
liter atm
.
.
SOxygen = 2.7 x 10 - 4 mol O2 / liter
This is adequate to sustain life in water!
Effect of Temperature: Heat of Solution
Solubility increases with temperature if the solution process is
endothermic:
Solute + Solvent + Heat
Solution
Solubility decreases with temperature if the solution process is
exothermic:
Solute + Solvent
Solution + Heat
7
Predicting the Effect of Temperature
on Solubility - I
Problem: From the following information, predict whether the
solubility of each compound increases or decreases with an increase in
temperature.
(a) CsOH
Hsoln = -72 kJ/mol
(b) When CsI dissolves in water the water becomes cold
(c) KF(s) H2O K+(aq) + F -(aq) + 17.7 kJ
Plan: Write a chemical reaction that includes heat being absorbed
(left) or released (right). If heat is on the left, a temperature increase
shifts to the equilibrium to the right, so more solute dissolves, and visa
versa.
Solution:
(a) The negative H indicates that the reaction is exothermic, so
when one mole of Cesium Hydroxide dissolves, 72 kJ of heat is released.
8
Predicting the Effect of Temperature
on Solubility - II
(a) continued
CsOH(s)
H2O
Cs+(aq) + OH -(aq) + Heat
A higher temperature (more heat) decreases the solubility of CsOH.
(b) When CsI dissolves, the solution becomes cold, so heat is absorbed.
H2O
CsI(s) + Heat
Cs+(aq) + I -(aq)
A higher temperature increases the solubility of CsI.
(c) When KF dissolves, heat is on the product side, and is given off
so the reaction is exothermic.
H2O
K+(aq) + F -(aq) + Heat
KF(s)
A higher temperature decreases the solubility of KF
Colligative Properties of Solutions
17.4) Vapor Pressure Lowering - Raoult’s Law
17.5) Boiling Point Elevation
and Freezing Point Depression
17.6) Osmotic Pressure
We’ll start by focusing on nonvolatile nonelectrolitic solutes
(e.g. sucrose in H2O)
Later: volatile solutes, electrolytic solutes
9
Raoult’s Law:
Psolvent = Xsolvent . P°solvent
X is the mole fraction
See Figure 17.9
Figure 17.8, Zumdahl
10
Example: Vapor Pressure Lowering
Problem: Calculate the vapor pressure lowering (∆P) when 175g of
sucrose is dissolved into 350.00 ml of water at 750C. The vapor
pressure of pure water at 750C is 289.1 mm Hg, and it’s
density is 0.97489 g/ml.
Plan: Calculate the change in pressure from Raoult’s law using the
vapor pressure of pure water at 750C. We calculate the mole
fraction of sugar in solution using the molecular formula of
sucrose and density of water at 750C.
Solution: molar mass of sucrose ( C H O ) = 342.30 g/mol
12
22
11
175g sucrose
= 0.51125 mol sucrose
342.30g sucrose/mol
350.00 ml H2O x 0.97489g H2O = 341.21g H2O
ml H2O
341.21 g H2O
= 18.935 mol H2O
18.02g H2O/mol
Vapor Pressure Lowering (cont)
Vapor Pressure lowering:
∆P = Xsolute . P°solvent
Xsucrose =
=
mole sucrose
moles of water + moles of sucrose
0.51125 mole sucrose
= 0.2629
18.935 mol H2O + 0.51125 mol sucrose
∆P = Xsucrose * PoH2O = 0.2629 x 289.1 mm Hg = 7.600 mm Hg
11
Boiling Point Elevation
Recall: The normal boiling point (Tb) of a liquid is the
temperature at which its vapor pressure equals atmospheric
pressure.
Nonvolatile solutes lower the vapor pressure of a liquid
Æ greater temperature required to reach boiling point
Boiling Point Elevation:
∆Tb = Kbmsolute
Kb = Molal boiling point constant for given liquid
msolute = molal solute concentration
Kb = Molal boiling point constant for given liquid
See Table 17.5
12
Freezing Point
Depression:
∆Tf = Kfmsolute
See Figure 17.3
Kf = Molal freezing point constant for given liquid
See Table 17.5
13
See Figure 17.12
Example: Boiling Point Elevation and Freezing Point
Depression in an aqueous solution
Problem: We add 475g of sucrose (sugar) to 600g of water. What will
be the Freezing and Boiling points of the solution?
Plan: Find the molality of the sucrose solution, and apply the equations
for FP depression and BP elevation using the constants from table 17.5.
Solution: Sucrose (C12H22O11) has molar mass = 342.30 g/mol
475g sucrose
= 1.388 mole sucrose
342.30gsucrose/mol
molality = 1.388 mole sucrose = 2.313 m
0.600 kg H2O
oC
∆Tb = Kb . m = 0.512
m
(2.313m)= 1.18oC
BP = 100.00oC + 1.18oC
= 101.18oC
o
∆Tf = Kf . m = 1.86 C(2.313 m) = 4.30oC
m
FP = 0.00oC -4.30oC= -4.30oC
14
Example: Boiling Point Elevation and Freezing Point
Depression in a Non-Aqueous Solution
Problem: Calculate the Boiling Point and Freezing Point of a
solution having 257g of napthalene (C10H8) dissolved into 500.00g of
chloroform (CHCl3).
Plan: Just like the first example.
Solution: napthalene = 128.16g/mol
chloroform = 119.37g/mol
molesnap = 257g nap =2.0053 mol nap
128.16g/mol
molality = moles nap = 2.0053 mol= 4.01 m
kg(CHCl3)
0.500 kg
o
∆Tb = Kb . m = 3.63 C(4.01m) = 14.56oC
normal BP = 61.7oC
m
new BP = 76.3oC
o
∆Tf = Kf . m =4.70 C (4.01m) =18.85oC
normal FP = - 63.5oC
m
new FP = - 82.4oC
Osmosis: The flow of solvent through a
semipermeable membrane into a solution
The semipermeable membrane allows solvent
molecules to pass, but not solute molecules
See Figures
17.15, 17.16
15
Osmotic Pressure, Π = MRT
(similar to ideal gas law!)
R = gas constant
M = molar concentration of solute
Determining Molar Mass from
Osmotic Pressure
Problem: A physician studying hemoglobin dissolves 21.5mg of the
protein in water at 5.0oC to make 1.5 ml of solution in order to
measure its osmotic pressure. At equilibrium, the solution has an
osmotic pressure of 3.61 torr. What is the molar mass (M) of the
hemoglobin?
Plan: We know Π, R, and T. We convert Π from torr to atm, and T
from oC to K, and then use the osmotic pressure equation to solve for
molarity (M). Then we calculate the number of moles of hemoglobin
from the known volume and use the known mass to find M.
Solution:
P = 3.61 torr . 1 atm = 0.00475 atm
760 torr
Temp = 5.00C + 273.15 = 278.15 K
16
Molar Mass from Osmotic Pressure
Concentration from osmotic pressure:
M = Π = 0.00475 atm
RT
0.082 L atm (278.2 K)
mol K
= 2.08 x10 - 4 M
Finding # moles of solute:
-4
n = M . V = 2.08 x10 mol
L soln
. 0.00150
L soln = 3.12 x10 - 7 mol
Calculating molar mass of Hemoglobin (after changing mg to g):
M =
0.0215 g
= 6.89 x104 g/mol
3.12 x10-7 mol
Colligative Properties of Solutions
17.4) Vapor Pressure Lowering - Raoult’s Law
17.5) Boiling Point Elevation
and Freezing Point Depression
17.6) Osmotic Pressure
We started with nonvolatile nonelectrolytes (e.g. sucrose/H2O)
Now let’s look at volatile solutes and electrolytes
17
Colligative Properties of Volatile Nonelectrolyte Solutions
From Raoult’s law: Psolvent = Xsolvent . P0solvent and Psolute = Xsolute . P0solute
Consider a solution having equal molar quantities of acetone and
chloroform, Xacetone = XCHCl3 = 0.500. At 350C, the vapor pressure of
pure acetone = 345 torr and pure chloroform = 293 torr.
¾ Determine the vapor pressure of the solution and the partial
pressure of each component. What are the mole fractions, X, of each
component in the vapor phase?
Pacetone = Xacetone . P0acetone = 0.500 . 345 torr = 172.5 torr
PCHCl3 = XCHCl3 . P0CHCl3 = 0.500 . 293 torr = 146.5 torr
P
From Dalton’s law of partial pressures we know that XA = PA
Total
P
Xacetone = Pacetone= 172.5 torr
= 0.541
Total
172.5 + 146.5 torr
Total Pressure = 319.0 torr
P
146.5
torr
XCHCl3 = CHCl3 =
= 0.459
PTotal 172.5 + 146.5 torr
Vapor is enriched in acetone!
18
Non-ideal solutions
ƒ Ideal behavior is approached when solute and solvent are involved
in similar intermolecular interactions (∆Hsoln = 0)
ƒ When weaker solvent-solute interactions occur, heat is removed
upon dissolving (∆Hsoln > 0)
Æ the observed vapor pressure is higher than ideal
ƒ When stronger solute-solvent interactions occur, heat is released
upon dissolving (∆Hsoln < 0)
Æ the observed vapor pressure is lower than ideal
Figure 17.11
Colligative Properties of Ionic Solutions
For ionic solutions we must take into account the number of ions present!
i = van’t Hoff factor = “ionic strength”, or the number of ions present
For Electrolyte Solutions:
vapor pressure lowering:
P = i XsoluteP 0solvent
boiling point elevation:
Tb = i Kb m
freezing point depression:
osmotic pressure:
Tf = i Kf m
π = i MRT
19
Non-ideal Behavior
of Electrolyte
Solutions
(0.05m aqueous)
See Table 17.6
Non-ideal
Behavior of
Electrolyte
Solutions
20
Gallery Section (p. 508)
Plane de-icing and car antifreezingethylene glycol (C2H6O2)
“Biological antifreeze” in fish- glycerol (C2H8O3)
Salts for de-icing streets- CaCl2
Water volume regulation in cellsextracellular Na+ and osmosis
(also, salt cured foods!)
Zone refinement- purification of crystals
Key theme in each: the inability of solutes to cross a
phase barrier changes the properties of the solvent.
21
The structure and function of a soap
“Micelles”- stabilize nonpolar colloids in polar solvents
22