1. No category

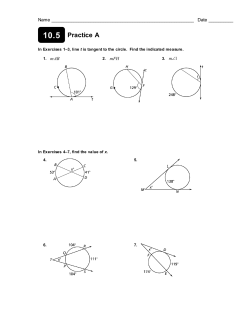
Geometry Info Sheet #38
The Unit Circle and Trigonometric Values
Definitions
Unit Circle: A circle in a coordinate plane with its center at the origin and a radius of one unit; it is used
to better understand sines and cosines of angles in right triangles; drawing a segment from
the origin (0, 0) to a point (x, y) on the circle makes an angle θ (measured from the positive
x-axis) and produces a right triangle with legs x and y such that cosθ = x and sin θ = y
A unit of angular measure equal to the measure of the central angle formed by an arc whose
length is equal to the angle's radius length in a unit circle; since the circumference of a circle
is 2 π r, a circle (360º) is equal to 2 π radians, so one radian is equal to almost 57.3 degrees
1
θ
x = cos θ
(cos θ, sin θ)
y = sin θ
Radian:
"Unit Circle Angles" by Jim Belk
is licensed under CC BY-SA 3.0
In a unit circle, and in trigonometry in general,
angles are frequently measured using radians,
as well as degrees.
In a unit circle, by using a radius of length 1 to form the hypotenuse of a right triangle, the trigonometric
ratios in the triangle will be dependent only on the lengths of the sides, since multiplying or dividing by 1
will not change any values.
Additional Information
The sine of an angle will always be a value between -1 (270º) and 1 (90º), inclusive.
The cosine of an angle will always be a value between -1 (180º) and 1 (0º), inclusive.
The tangent of an angle will always be a value between -1 (135º) and 1 (45º), inclusive.
The tangent of an angle is undefined for angles with measurements of 90º and 270º.