1. No category

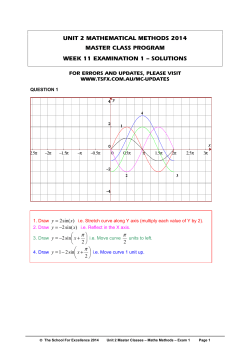
1995 HKCEE MATHS Paper II
1
Round off the number 0.044449 to 3 significant
5
2 6
figures.
2
A.
0.04
B.
0.044
D. 0.0444
C.
0.045
E. 0.0445
x y
 1 , then
xy
If
y=
6
A.
1 x
x
B.
x 1
x
D.
x
1 x
E.
C.
then k =
4
A.
100
B.
98
D.
100
C.
98
E.
198
 a6
Simplify  12
b
A.




C.
0
8
9
B.
b
a9
D.
a
b 18
C.
a4
b8
E.
1
a b
6
2
D.
6
2
E.
6
The L.C.M. of x 3  x and x 4  1 is
A.
x 1
B.
x  1x  1


x  1x  1x  1x  x  1
x x  1  x  1 x  1
x x  1 x  1 x 2  1
2
2
2
2
2

4 x 
Solve the simultaneous equations: 
2 x 

y
6
3
y
 1
6
1
B. x   , y  12
2
D. x 
1
, y  12
2
1
, y  12
2
E. x 
5
7
,y
24
2
C. x 
b8
a4
CE MATHS Paper II


1
A. x   , y  12
2
2
3
18
95
B.
E.
If f  x   x 99  99 x  k is divisible by x + 1 ,
2 6
 6
D.
1 x
1 x
1

A.
C.
x
x 1
7
3
1
Which
of
the
following
shaded
regions
y  0

represents the solution of  x  y  3
x  2 y  0

4 12
A.
Ⅰ
B.
Ⅱ
C.
Ⅲ
D.
Ⅳ
E.
Ⅴ
P.1
B. $ P1  r %   $ P
Find the values of x which satisfy both  x  4
9
and
n
2 x  16
 2
3
C. $ P 1  r %   $ P
2n
n
 r 
D. $ P1  %   $ P
 2 
A.
4 x 5
B.
x  4
D.
x5
C.
x  4
E.
x5
 r 
E. $ P1  % 
 2 
10 If 3 x 2  6 x  1  3 x  b 2  c , then c =
11
A.
8
B.
2
D.
1
3
C.
0
E.
1
2n
 $P
14 In the figure, ABCD is a trapezium. Find its area.
x and y are two variables. The table below
shows some values of x and their corresponding
A.
36cm2
B.
45cm2
C.
48cm2
D.
72cm2
E. 90cm2
values of y.
x
2
3
6
12
y
36
16
4
1
15 In the figure, the solid consists of a cylinder and
a right circular cone with a common base which
is a circle of radius 3cm. The height of the
cylinder is 10cm and the slant height of the cone
Which of the following may be a relation
is 5cm. Find the total surface area of the solid.
between x and y ﹖
A.
x y
B.
x y
C.
x
A. 75 cm2
D.
1
E.
y
x
x
1
y
B. 84 cm2
1
y2
D. 105 cm2
C. 93 cm2
E. 114 cm2
12 If 125x  25 y and x, y are non-zero, find x : y .
16
A.
1 : 25
B.
1:5
D.
3:2
C.
2:3
E.
5:1
13 Find the interest on $P at r% p.a. for n years,
cos 2 
1 
1  sin 
A.  sin
D.

C. sin  2
E.
sin  1  sin  
1  sin 
compounded half-yearly.
A. $ P 1  2r %   $ P
n
95
CE MATHS Paper II
sin  1  sin  
1  sin 
B. sin
P.2
17
If 0  x  2 , solve sin x 
1
correct to 3
3
20 In the figure, the bearing of B from A is
significant figures.
A. 0.327 or 2.81
A.
015º
B.
045º
B. 0.327 or 3.47
D. 0.340 or 3.48
C.
075º
C. 0.340 or 2.80
E. 0.340 or 5.94
D.
165º
E.
345º
18
1
The greatest value of
A.
1
2
B.
1
4
D.
1
E.
C.
21sin x
is
2
21 In the figure, BDC is a straight line. Arrange AD,
4
BD and DC in ascending order of magnitude.
19 According to the figure, which of the following
must be true﹖
A. AD  BD  DC
B. AD  DC  BD
A.
a 2  b 2  c 2  3bc
C. DC  AD  BD
B.
a 2  b 2  c 2  bc
D. DC  BD  AD
C.
3
a b c 
bc
2
D.
a 2  b 2  c 2  bc
E.
a 2  b 2  c 2  3bc
2
2
E. BD  AD  DC
2
22 In the figure, ABCD is a semicircle. CAD =
A. 25º
B. 40º
C. 45º
D. 50º
E. 65º
95
CE MATHS Paper II
P.3
26 In the figure, ADE=ACB. Find x.
23 In the figure, O is the center of the circle,
POQR is a straight line. TR is the tangent to the
circle at T. PRT 
A.
20º
B.
35º
C.
45º
A.
4
D.
50º
B.
8
D. 12
E.
70º
C.
10
E. 16
27 In the figure, the equation of the straight
24 In the figure, ABCD is a cyclic quadrilateral. If
line L is
DAB  110 and BC = BD, find DAC.
A.
20º
B.
35º
C.
40º
D.
55º
E.
70º
A. x  3  0
B. x  y  3  0
C. x  y  3  0
D. x  y  3  0
E. x  y  3  0
25 In the figure, AB = AC and AD = AE. DAC=
28 In the figure, OA=AB. If the slope of AB is m,
find the slope of OA.
95
A.
45º
B.
50º
C.
55º
D.
60º
E.
65º
CE MATHS Paper II
A.
1
B.
1
m
C.

D.
m
E.
m
1
m
P.4
29 The table below shows the centers and radii of
30 In the figure, the equation of the circle is
two circles C1 and C2 .
C1
C2
Center
2,2
5,2
Radius
3
2
Which of the following may represent the
relative positions of C1 and C2 ﹖
A.
x2  y2  5  0
B.
x 2  y 2  2x  y  0
C.
x 2  y 2  2x  y  0
D.
x 2  y 2  4x  2 y  0
E.
x 2  y 2  4x  2 y  0
31 In a shooting game, the probability that A will hit
a target is
is
3
and the probability that B will hit it
5
2
. If each fires once, what is the probability
3
that they will both miss the target﹖
A.
1
3
B.
1
4
D.
2
15
C.
2
5
E.
11
15
32 The figure shows that Mr. Chan has 3 ways to
leave town X and Mr. Lee has 2 ways to leave
town Y. Mr. Chan and Mr. Lee leave town X and
town Y respectively at the same time. If they
select their ways randomly, find the probability
that they will meet on their way.
95
CE MATHS Paper II
P.5
A.
1
2
B.
1
3
D.
1
6
C.
2
3
E.
5
6
B.
1
C.

1 x
1 x
other four numbers is
B.
a n a  6 2a  5
C.
a n a  62a  5
A.
4
B.
10
D.
17
D.
a n 1 a  6 2a  5
C.
16
E.
25
E.
a n 1 a  6 2a  5
following is/are true﹖
I. The mean of A = the mean of B.
E.
x
x 1
2
A. a n  6 2a  5
mean of the first 5 numbers is 8, the mean of the
symmetric distributions A and B. Which of the
x
1 x2
36 Factorize 2a n1  7a n  30a n1 .
33 The mean of a set of 9 numbers is 12. If the
34 The figure shows the frequency curves of two
D.
37
x
 y 
  11  
y
 x 
Simplify
.
x y

y x
A.
x y
x y
B.

C.
x y
x y
II.The inter-quartile range of A > the
x y
x y
x y
x y
D.

E.
1
inter-quartile range of B.
III.The standard deviation of A > the standard
35
c c
 
a b
deviation of B.
then
A.
I only.
A.
7
10
B.
I and II only
B.
1
D. log 7
C.
I and III only
D.
II and III only
C.
7
E.
E.
I, II and III
x
1
If f  x  
, then f   f  x  
1 x
 x
A.
95
38 If 5 a  2 b  10 c and a, b, c are non-zero,

1
2
CE MATHS Paper II
39 If
, 
are
the
1
1

log 2 log 5
roots
of
the
equation
x 2  4 x  3  0 , then  2     2 
A.
13
B.
5
D.
16
C.
13
E.
19
P.6
40 Find the range of values of k such that the
B.
1
D.
10
equation x 2  k  2 x  1  0 has real roots.
C.
2
E.
100
44 The marked price of a toy is $120 and the
percentage profit is 60%. If the toy is sold at a
A. k  4
B. 0  k  4
D. k  0 or k  4
C. 0  k  4
E. k  0 or k  4
41 Which of the following may represent the graph
of y   x 2  3x  10 .
discount of 20%, the profit is
A.
$14.40
B.
$21.00
D. $33.60
C.
$24.00
E. $48.00
45 In the figure, O is the center of the circle. Find
the area of the major segment ABC.
A.

4
r2
B.
3 2
r
4
C.
 1  2
  r
 4 2
D.
 3 1  2
 r

 4 2
E.
 3 1  2
 r

 4 2
46 In the figure, C1 and C2 are two circles. If
42 In an A.S., the sum of the first 2 terms is 3 and
area of region I : area of region II : area of region III
the sum of the first 3 terms is 2. The common
= 2 : 1 : 3,
difference is
then radius of C1 : radius C2 =
A.
B.
C.

5
3
1
1
A. 9 : 16
D.
E.
5
3
7
3
43 If the geometric mean of two positive numbers
B. 2 : 3
C. 3 : 4
D.
2 : 3
E.
3 :2
a and b is 10, then log a  log b 
A.
95
1
2
CE MATHS Paper II
P.7
47 In the figure, DE=DB, AC=13 and BC=5. Area
of ADE : Area of ACB 
50 The figure shows the graph of the function
A. y  cos
A.
64 : 169
B.
5 : 13
C.
4:9
D.
8 : 13
E.
2:3
B. y 
x
2
1
cos x
2
C. y  cos x
D. y  2 cos x
E. y  cos2 x
48 In the figure, a solid wooden sphere of radius
3cm is to be cut into a cube of side x cm. Find
51 In the figure, ABCDEFGH is a cuboid. tan 
the largest possible value of x.
A.
1
3
1
B.
A.
C.
3 2
B.
2 3
D.
3
2
2
C.
3
E.
3
3
1
3
D.
E.
3
49 If 0  x  360 , the number of points of
intersection
95
of
the
graphs
y  sin x
and
52 In the figure, PB touches the semicircle ADB at
y  tan x is
B. PD =
A.
1
A.
B.
2
D.
4
C.
3
E.
5
CE MATHS Paper II
d
2 cos
B. d sin  tan
C.
d
sin  tan 
D.
d cos
tan 
E.
d tan 
cos
P.8
53 In the figure, a + b + c + d + e + f =
A.
270º
B.
360º
C.
450º
D.
540º
E.
720º
54 According to the figure, which of the following
must be true﹖
A.
ab  cd
B.
ad bc
C.
a  b  c  d  360
D.
a  b  c  d  540
E.
2a  2b  c  d  720
END OF PAPER
95
CE MATHS Paper II
P.9