1. No category

G.GMD.1 STUDENT NOTES WS #6
1
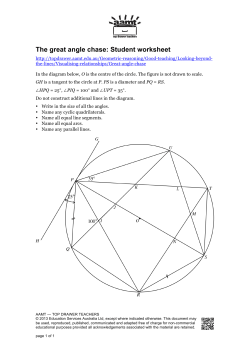
THE CIRCLE
The circle definite poses a different type of problem when trying to derive the area of it. It obviously needs to
be approached differently from the polygons that we have already discussed because of its shape. We are
going to use an informal limit argument to help us determine its area formula. Limits in general are an upper
level mathematical idea but when presented in a visual way they can be understood at earlier levels.
CIRCLE – DISSECTION (LIMIT ARGUMENT)
Once again we are going to take the original shape and cut it up into smaller pieces to form a shape that we
already know a lot about.
The first dissection cuts are 90° sectors. When we
put the four pieces together to form a new shape we
get something that isn’t very recognizable.
The second dissection cuts are 45° sectors. When we
put the eight pieces together it seems to form a more
recognizable shape… maybe a parallelogram but the
sides are ‘bumpy’.
The third dissection cuts are 30° sectors. This
definitely is making the shape look a lot more like a
parallelogram.
Finally, our fourth attempt we use 15° sectors. This
makes the new shape more and more parallelogram
like… that is the intent of the limit argument.
If we continued this process down to an angle size of 1° or even 0.0001° the
new shape would approach the parallelogram shape. This is the limit
argument. As we decrease the angle size of the sector the area begins to
approach the shape of a parallelogram. Now lets look at the dimensions of
that parallelogram. The height approaches the radius, r, of the circle. Notice
how r is NOT the height in the second example but by the fourth example r
looks to be very close to the height. Now we need to look at the base value.
The base value is half of the circumference of the circle, the circumferene of
the circle is half divided into two halves. If we put this together we get Area =
½ (2πr)(r) = πr2 using this informal limit argument.
r
r
r
Acircle = πr2
r
πr
G.GMD.1 STUDENT NOTES WS #6
2
AREA OF A CIRCLE SECTOR
A sector of a circle is a part of the circle formed by two radii and the circumference. It looks like a pie piece.
Often we are asked to calculate circle sectors whether it be half of a circle, a semicircle, or a quarter of a circle.
These divisions are easy to visualize and calculate. If you want to calculate the area of a semicircle you divide
the area by two or in the case of a quarter you divide by four. It becomes more difficult if the sector has a 49°
central angle…. What do we divide by now?
x°
49°
180
1
πr2 = πr2
360
2
1
x
49
πr2 = πr2
Area =
πr2
Area =
πr2
360
4
360
360
Think of a circle as a percentage of the circles total area, so all
AREACIRCLE SECTOR = x° π r 2
we do it create a percentage based on the central angle to the
360
total angle value, 360°. This calculates a circle sector.
Area =
90
Area =
Find the AREA of each circle or circle sector or composite shape.
4 cm
120°
30°
9 cm
_____________(E)
A = π r2
2
A = π (4) = 16π cm
2
_____________(E)
A=
θ
π r2
360
120
A=
π (9)2 = 27π cm 2
360
12 cm
_____________(E)
θ
π r2
360
30
A=
π (12) 2 = 12π cm 2
360
A=
3 cm
7 cm
5 cm
6 cm
10 cm
1
1
A = (5 + 10)(3) + π (5) 2
2
2
A = 22.5 + 2.5π cm 2
1
A = (6)(6) + (3) π (3) 2
2
A = 36 + 13.5π cm 2
1
A = (10 + 17)(10) − π (5) 2
2
A = 135 − 25π cm 2
G.GMD.1 WORKSHEET #6
NAME: ____________________________ Period _______
1. Explain how we use the informal limit argument to explain where the formula for the area of a circle
comes from? Draw a diagram to help your explanation.
2. Determine the area of the circle.
a) r = 3 cm
c) r =
3
cm
5
Area = _______________ (E)
b) d = 12 cm
Area = _______________ (E)
Area = _______________ (E)
d) d =
5
cm
4
Area = _______________ (E)
3. Determine the area of the circle.
a)
b)
c)
d)
32 cm
4 cm
16 cm
Area = ____________(E)
Area = ____________(E)
10 cm
Area = ____________(E)
Area = ____________(E)
c)
d)
4. Determine the area of the circle sector.
a)
b)
30°
4 cm
270°
3 cm
Area = _____________(E) Area = ____________(E)
83°
9 cm
8 cm
Area = __________ (2 dec.)
120°
Area = ____________(E)
1
G.GMD.1 WORKSHEET #6
2
5. Determine the area of the following figures. (Lines that appear to be perpendicular are perpendicular and
lines that appear to be parallel are.)
a)
b)
Area = _______________________ (E)
c)
Area = _______________________ (E)
d)
Area = _______________________ (E)
e)
Area = _______________________ (E)
f)
Area = _______________________ (E)
Area = _______________________ (E)
G.GMD.1 WORKSHEET #6
3
6. Determine the area of the SHADED region.
(Lines that appear to be perpendicular are perpendicular and lines that appear to be parallel are and lines that
appear to be tangent are.)
a) A square with a side of 6 cm.
Area of shaded region = __________________ (E)
b) A rectangle with dimensions of 6 cm and 10 cm.
Area of shaded region = __________________ (E)
c) Two concentric circles with radii of 2 cm and 3 cm. d) A 12 cm square inscribed in a circle.
Area of shaded region = __________________ (E)
e) A circle with an inscribed triangle.
Area of shaded region = __________________ (E)
Area of shaded region = __________________ (E)
f) Diameter of the circle is 12 cm.
Area of shaded region = __________________ (E))
*o*r,
G.6MD.1 WORKSHEET #6
W
period
1' Explain how we use the informat timit argument to explain where the
formula for the area of a circle
comes from? Draw a diagram to help your explanation.
?ivrle 'h^r- cnzlc iw{oyr,n g- sywar.t( ;,r,*,W Sez-Wt, e^-L fk't^-! a'L \+^'ha l.- l'w''"*
rt
# {avgo. A- PaxvuLU,Loctrvo*u 1;Wr' g{\u^(rL. 1,U4- d.,\re.o-r-, tsv'g a,V<' qPaoY"^o!'bh
lnAlWY;,o[rt5 a^L Basc-=Tu- Ct^\? c,Yt;t,'4*c)" .S.,
IJUIJ lu*r llr P h +1,^-- ?&t/b"t/n-[ogrr''-rs d ''v^-'-'"gr'€ u>-u- A"'y
r (rv) +
UJ{^}-^-
TrL
2. Determine the area of the circle.
a)
.J
r=3cm
=
Area=
(E)
b)d=12cm
Area
Area =
(E)
d)d= lcm
Area=
a
c)r=-cm
5
Y=
3. Determine the area of the circle.
a)
b)
c)
Area = _(E)
Area =
Area =
sLW c,^-
(E)
fr lu
rq
5,
_(E)
Area
=
loo
I
Cnz 1r;
4. Determine the area of the circle sector.
a)
b)
d)
/
I
cml
t
I
\
/
'6
1(g
/
-
q-(r);
7
Y
9cm
'ff
r (f)
t@)'
* 'r (tr)
Area =
(E)
Area=
4u ruu 6y
Area=
(2dec.) Area=
ZTT C^L 1fy
G.GMD.I
WORKSHEET
#6
2
5. Determine the area of the following figures. (Lines that appear to be perpendicular are perpendicutar and
lines that appear to be parallel are.)
a)
Scm
n
12
b)
n
II
5
*,.-
tfn
Area =
c'lr
(4G t?o l{
*rt
(E)
,
Area
= I,ff + 1f cr^L
(E)
c)
4
I0 rm
+ q
(tr) r
ru '-trb)L
l$ cm
3O crn
(t;)
L
ln t ttr ->tr
(E)
Area
= {ta *
[b
f- c ww (E)
f ru\'| +)
l>r #tr
Area =
(E)
Area=
"t
Efctx-
(E)
G,GMD,I
WORKSHEET
#6
6. Determine the area of the SHADED region.
(Lines that appear
to be perpendicular are perpendicular and lines that appear to be parallel are and lines that
appearto be tangent are.)
a) A square
with
a side
of 6 cm.
b) A rectangle with dimensions of 6 cm and 10 cm.
b
(t')
- rt (^'
16 cm
6cm
Area of shaded region =
c) Two concentric circles
(E)
with radii of 2 cm and 3 cm.
Area of shaded region
(E)
e)A circle with an inscribed triangle.
1ty
d)A 12 cm square inscribed in a circle.
,ltrrrltrt
Area of shaded l'€$lOh =
= 6o * QIf C^t
Area of shaded region
T (u,b)z * o(rz)
-7 >a *
1,,p,(
(V*
= 1Zt -
9^'
(E)
f) Diameter of the circle is !2 cm.
a.r6**
I o."l-
t (d'
---
Area of shaded region =
(E)
Area of shaded region =
(tr
2_
cy4>
(E))