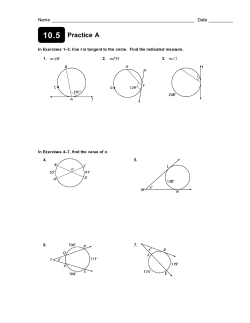
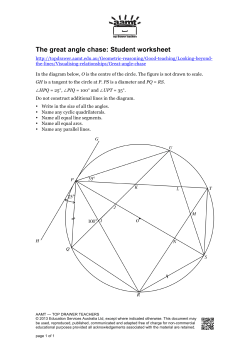
GT/Honors Geometry
April 16 to May 1
Date
Topic
Homework
Wednesday
4/15
Thursday
4/16
Friday
4/17
Test 3: Surface area and volume of
solids.
TB pg 660: 1-15
12-1 Tangent Lines
p. 665 (1-4, 6, 8-15, 20, 22, 23, 25, 26, 28)
Monday
4/20
Tuesday
4/21
Wednesday
4/22
12-2 Chords and Arcs (cont’d)
12-3 Inscribed Angles (cont’d)
Quiz on 12-1 and 12-2
WS – Practice 12-3A
Thursday
4/23
12-4 Angle Measures
in Circles
p. 691 (1-8)
WS Finding Angle Measures in Circles 1 and 2
Friday
4/24
12-4 Segment Lengths in Circles
Monday
4/27
Tuesday
4/28
Wednesday
4/29
Thursday
4/30
Friday
5/1
12-5 Circles in the Coordinate Plane
12-2 Chords and Arcs
12-3 Inscribed Angles
p. 673 #1-18
Page 674-675 # 26, 27, 30-32, 33,34, 42,
44,45,46,48,49)
p. 681 (5-24, 28, 42-44)
p. 691 (9 - 28, 36, 40, 41) p. 685
Quiz 12-3 and 12-4
Review for test on circles
TEST over Circles – 12-1 to 12- 5
TEST over Circles – 12-1 to 12- 5
p. 697 (1, 3, 6, 8, 11, 12, 14, 17, 20, 21, 24, 27, 29,
32, 33, 35, 37, 40, 42-47, 53, 55, 57)
Review for Test on Circles
TBA
Tues 4/ 16: 12.1 Study Guide (Tangents)
Theorem 1: Line tangent to a circle  line  to radius at tangent point
B
C


A
Theorem 2: Tangent segments from same exterior point are congruent.
B

A
C

D
External Common Tangent
Internal Common Tangent
Polygon circumscribed about a circle
C
Ex. 1 BC = 3, AF = 9.5, perimeter of ACE = 50. Find DE.
D
B
A
E
F
Ex. 2 AD = DB = 16; EC = 12. Find AE.
C
E
A

F
B
D
Ex. 3 mEML = 66; MK = 15; KL = 36
E
mMKL = _______
mELM = _______
P
M
EL = _______
m KPE = ______
L
K
ML = _______
PL = ________
Ex. 4 Circles A, B, and C are tangent. AB = 11; BC = 4; AC = 9. Find the radius of each circle.
A

C

B
Ex. 5 A belt fits tightly around two circular pulleys, as shown. Find the distance between the
centers of the pulleys.
35 in.
14 in.
8 in.
B
4/17 – 4/20: 12-2 Arcs and Chords
A
In a circle or in congruent circles, two minor arcs are
congruent if and only if their corresponding chords are
congruent.
●
C
D
C
E
If a diameter is perpendicular to a chord, then it bisects the
chord and its arc.
D
B
If a diameter bisects a chord (that is not a diameter), then
it is perpendicular to the chord.
●A
In a circle, the perpendicular bisector of a chord contains
the center of the circle.
B
D
In a circle or in congruent circles, two chords are congruent
if and only if they are equidistant from the center.
A
●M
C
Ex. 1 OD = 15 and CD = 24. Find OE and EG.
O
●
E
C
D
G
Ex. 2 MN=NP=PQ; mMQ =120°. Find m NP .
M
N
●
P
Q
Ex. 3 PQ  RM
a) Name an arc congruent to QR .
Q
R
A
M
b) If PR = 13 and RM = 24, find PA.
●
P
E
V
Ex. 4 TR = 9 and EN = 10. Find RA.
R
T
A
●
N
S
B
Ex. 5 In
Find AG.
C, GC = CH, CG  AB , CH  DE and DE = 24.
A
G
●C
D
H
E
Ex. 6 Suppose a chord is 20 inches long and is 24 inches
from the center of the circle. Find the length of the radius.
●
T
Ex. 7 Circles C and H are congruent. TM is a chord of both
circles.
a. Draw segments CT and CM. How are they related?_____________
b. Draw segments HT and HM. How are they related?_____________
c. What kind of quadrilateral is CTHM?_________________
d. What is the measure of TKH? ______ Why?___________________
C
●
K
M
●H
A
4/ 21-22: 12-3 Notes – Inscribed Angles
E
 An angle is inscribed if its vertex is on the circle
and its sides contain chords of the circle.
C
_________ is an inscribed angle.
D
B
 If an angle is inscribed in a circle, then the measure of the angle equals one-half the measure of its
intercepted arc.
A
ABC intercepts _______
If m AC = 100 then mABC = ________.
If mABC = 70, then m AC = ______
C
B
 If two inscribed angles of a circle or congruent circles intercept congruent arcs or the same arc,
then the angles are congruent.
3 intercepts _______; 4 intercepts _______
1 intercepts _________
Since m
2 intercepts _________ so ___________
=m
, ________________
80
D
B
C
A
1
A
4
3
2
C
B
D
80
A
 If an inscribed angle of a circle intercepts a
semicircle, then the angle is a right angle.
C
D
B
A
 The opposite angles of a quadrilateral inscribed in
a circle are supplementary.
N
R
G
 The measure of an angle formed by a tangent and a chord is
half the measure of the intercepted arc.
mC =
1
2
B
B
●
●D
●
m BDC
●
●
C
D●
●
●
C
A
1) Name an inscribed angle.
B
2) Name an arc intercepted by BAC
42
P
C
3) If mBPC = 42, find mBAC
J
4) Find x
L
5) RS and TU are diameters of
Find BRT and mTRS.
A.
N
x
100
126°
K
6) In A , PQ  RS and m1 = 38° and m QR = 28°. Find:
mT = ________
m2 = _________
m3 = _________
m4 = _________
m PT = _________
R
Q
4
1
P
3
S
2
A
T
7) In
Z , AB DC , m BC = 94, mAZB = 104. Find:
A
m AB = _______
mBAC = _________
mADB = __________
m AD = ___________
m CD = ___________
mDAC = ___________
mAEB = ____________
8) Quadrilateral QRST is inscribed in C . If
mT = 95 and mS = 100, find mQ and
mR.
Q
R
●C
T
S
Z
E
D
C
9) In
Q , AC is a diameter, m CD =68 and m
BE =96. Find:
m  ABC = _____
m  BDE = _____
m  CED = _____
m AD = _______
B
4/ 23: 12-4 Secants, Tangents, and Angle Measures
C
●
H
●
B
●
A●
●
D
G●
●
E
F
1
mA  (mCE  mBD)
2
K
●
●
●
I
1
mF  (mIH  mGI)
2
●C
●M
J●
●
D
E
●
B
A●
●
L
1
mJ  (mKML  mKL)
2
●
or
1
mCEB  (mBC  mAD)
2
mJ  mKL  180°
Find the measure of each numbered angle.
1.
2.
52°
1
110°
3.
40°
100°
2
3
80°
134°
T , find the value of x.
Given
4.
5.
6.
130°
20°
100°
T
●
T
●
x°
x°
T
70°
●
50°
x°
In
K , m OB = 98°, m OY =28°, m YD =62°, and m DA =38°. Find:
7. m AB
8. m1
B
5
1
9. m2
K
●
2
10. m3
4
11. m4
12. m5
A
D
O
3
Y
Geometry: WS H/W 4/23
Name_________________________________
Worksheet – Finding Angle Measures in Circles
Date_____________________Period_______
1. GE is a diameter of circle O. IH and KJ are tangents of circle O.
m FE =40, m ED =20, m DC =76, m AB =30, m GA =10. Find:
H
E
F
(a) mALB=__________
(g) mACK=__________
(b) mBLC=__________
(h) mFGE=__________
(c) mJCA=__________
(i) mEFG=__________
(d) mEOD=__________
(j) mGFO=__________
D
I
J
O
C
L
(e) mFEG=__________
(k) mIFG=__________
(f) mFOE=__________
(l) mHFE=__________
B
G
A
K
2. DB is a diameter of circle O. ED and EA are tangents of circle O
m AB =76 and m DC =110. Find:
(a) m BC =__________
(i) mEAD=__________
(b) m AD =__________
(j) mBAF=__________
(c) mDOA=__________
(k) mDCA=__________
(d) mDAO=__________
(l) mDGC=__________
(e) mOAC=__________
(m) mDBA=__________
(f) mCAB=__________
(n) mADO=__________
(g) mEDA=__________
(o) mODC=__________
(h) mDEA=__________
(p) mHDC=__________
H
D
C
O
G
E
B
A
F
3.
AE is a tangent. mFAE=85, mHJG=55, mGAK=75, m AB =40, m BC =16, m CD =10
Find:
G
(a) m DF =_________
(i) mHAG=________
(b) m FG = _________
(j) mGAF=________
(c) m GH =_________
(k) mALC=________
(d) m HA =_________
(l) mFIB=_________
(e) mAFD=________
(m) mKEH=________
(f) mAGC=________
(n) mHEG=________
(g) mAHB=________
(o) mGEF=________
F
L
H
D
J
C
I
B
K
E
A
(h) mKAH=________
4. RH and KE are diameters of circle O. FE and AK are tangents. mEOH=70, m CR =10, m
DE =60. Find:
(a) m RK =___________
(j) mKEH=________
(b) m KH =__________
(k) mHEG=________
(c) m HE =__________
(l) mRHE=________
(d) mKAE=________
(m) mRHK=________
(e) mHBE=________
(n) mHKO=________ A
(f) mKCE=________
(o) mEKD=________
(g) mEMD=________
(p) mCKD=________
(h) mKFE=________
(q) mKLH=________
(i) mCEK=________
(r) mKJH=________
K
H
O
L
J
G
R
B
C
M
E
D
F
4/24: 12-4 Segment Lengths
∆ABD ~ ∆EBC by AA~.
Therefore,
E
A
AB BD
and AB  BC  EB  BD

EB BC
d
a
B
c
D
b
C
E
Ex. 1 Find x.
3
9
Ex. 2 Find CD in
x
C.
10
6
12
●
C
B
D
8
G
A
Ex. 3 In
a)
b)
c)
d)
e)
A , diameter RP  TS , TS = 10, and RE = 3. Find:
TE = ______
ES = ______
PE = _______
PR = _______
Radius of A = _______
∆SCN ~ ∆SAE by AA ~
Therefore,
Ex. 4 Find x.
S
E
T
● A
P
C
SC SN
and SC  SE  SA  SN

SA SE
(outside  whole  outside  whole)
R
S
b
a
E
c
N
A
Ex. 5 Find x.
13
x
8
3
4
7
3
x
d
∆ECD ~ ∆EBC by AA ~
Therefore,
C
c
EC ED
and EC2  ED  EB

EB EC
[(outside)2  outside  whole]
Ex. 6 Find x.
a
E
B
D
Ex. 7 Find x.
8
4
x
12
9
x
Ex. 8 Given the tangent and two secants to the circle, find the value of each variable to the
nearest tenth.
a = __________
12
x
x = __________
y = __________
9
a°
60°
8
y
175°
b
Notes 4/27 - 12.5 Circles in the Coordinate Plane
A circle is defined to be the set of points in a plane that are equidistant (length of the radius)
from a given point (center). If the center is at (0,0) then it will look like the following:
 (x,y)
One side of the triangle has length x and the other side of the triangle has length y so using
Pythagorean theorem we get the relationship:
x2 + y2 = r2
If the center is not at the origin, say it is at the point (2,5) the graph would look like the
following:
 (x,y)

(2,5)
That means that the horizontal side of the right triangle is x-2 and the vertical side of the
triangle is y-5. Using Pythagorean Theorem we get:
(x-2)2 + (y-5)2 = r2
In general, an equation for a circle with center at (h, k) and a radius of r units is:
(x-h)2 + (y-k)2 = r2
Examples: Given the equation, name the center and radius:
(1) (x+2)2 + (y-3)2 = 49
(2) x2 + (y-1)2 = 8
(3) Write an equation for a circle with center C(1, -2) that passes through the point (2, 2).
(4) Write an equation for a circle with center C(-3,6) and a diameter of 6 units.
(5) Write an equation for the circle where the segment joining A(-1,4) and B(5,2) is a diameter.
y
(6) Write the equation of the circle:
●
x
(7) The graphs of x = 4 and y = -1 are tangent to a circle that has its center in the third
quadrant and a diameter of 14. Write an equation of the circle.
(8) Algebraically, find the points of intersection of this pair of graphs. Make a sketch to check
your answer.
(x  2)2  (y  3)2  25 and y  x  2
Homework: page 697 (1, 3, 6, 8, 11, 12, 14, 17, 20, 21, 24, 27, 29, 32, 33, 35, 37, 40, 42-47, 53, 55, 57)