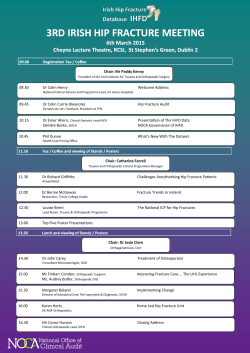
CHARACTERIZATION OF INTRALAMINAR
Analytical cohesive model for Compact Tension specimen Girona, 22 July 2013 Characterization of the intralaminar fracture cohesive law A. Ortega, P. Maimí., E. V. González. Madrid, 8th April 2015 (1) Characterization of the intralaminar fracture cohesive law Outline 1 – Direct method: analytic model 1.1 – Dugdale’s Condition 1.2 – Validation of the model 2 – Inverse problem 3 – Results 4 – Conclusions Madrid, 8th April 2015 (2) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 Preamble: Why use a cohesive model? Quasi-brittle materials: – Exhibit no hardening prior to the material failure. – Need a relatively high amount of energy to propagate a crack. – Develop a Fracture Process Zone relatively large compared to other problem dimensions. In this scenario, Linear Elastic Fracture Mechanics (LEFM) cannot be used to predict the crack growth. – A cohesive model is introduced to take into account the fracture mechanics at the FPZ. – The cohesive law is considered to be a material property. (3) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1 – Direct method To obtain the load-displacement (P-u) curve of a Compact Tension (CT) specimen taking into account the cohesive stresses at the Fracture Process Zone (FPZ). (4) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1.1 – Dugdale’s Condition: a superposition problem (5) Characterization of the intralaminar fracture cohesive law 1.1 – Dugdale’s Condition Madrid, 8th April 2015 (6) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1.1 – Dugdale’s Condition: determination of the cohesive stresses (7) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1.1 – Dugdale’s Condition: determination of the cohesive stresses (8) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1.1 – Dugdale’s Condition: Inputs and outputs (9) Characterization of the intralaminar fracture cohesive law 1.1 – Direct method. Madrid, 8th April 2015 (10) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1.2 – Model validation Excellent agreement with FEM for a linear cohesive law. (11) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 1.2 – Model validation As proven, the analytic model is equivalent to a FEM solution Advantages of analytic model over FEM: – Extremely fast computing time (<1s vs ~10min). – Any random CL shape. Advantages of FEM over analytic: – Easier to implement for any geometry. – Analytic only solved for isotropic material (can be implemented for orthotropic materials). (12) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem Madrid, 8th April 2015 (13) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: The FPZ formation Madrid, 8th April 2015 (14) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: The FPZ formation Madrid, 8th April 2015 (15) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: The FPZ formation Madrid, 8th April 2015 (16) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (17) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (18) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (19) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (20) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (21) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (22) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (23) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (24) Characterization of the intralaminar fracture cohesive law 2 – Inverse problem: Solution algorithm Madrid, 8th April 2015 (25) Characterization of the intralaminar fracture cohesive law 3 – Results Quasi-isotropic woven glass fabric [(0/45)5]S. Madrid, 8th April 2015 (26) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 3 – Results The CL shape depends on the number of points used to do the fitting. (27) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 3 – Results The CL shape depends on the number of points used to do the fitting. (28) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 3 – Results The CL shape depends on the number of points used to do the fitting. (29) Characterization of the intralaminar fracture cohesive law Madrid, 8th April 2015 3 – Results The CL shape depends on the number of points used to do the fitting. (30) Characterization of the intralaminar fracture cohesive law 4 – Overview Madrid, 8th April 2015 (31) Analytical cohesive model for Compact Tension specimen Thank you for your attention. Girona, 22 July 2013 (32) Analytical cohesive model for Compact Tension specimen Girona, 22 July 2013 (33)
© Copyright 2025