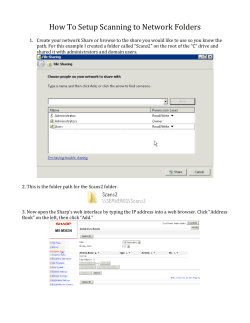
EN 14 101 Engineering Mathematics I
COMBINED FIRST AND SECOND SEMESTER B.TECH (ENGINEERING)
EXAMINATION; EN 14 101 – ENGINEERING MATHEMATICS I
Time: 3 Hours
Max: 100 marks
PART A: Analytical/problem solving SHORT questions
Answer Eight questions out of Ten (Each Question carries 5 marks)
1. Evaluate lim
−
x−
− −l g
2 . If x=u(1+v),y=v(1+u) Find
∂ ,
∂
,
3. Discuss the convergence of∑∞= sin
4. Ify=xn logx, Show that yn+1=
!
5. Using Cayley Hamilton find A2 if A=
6. Reduce the matrix A=
−
into Echelon form
−
7. If f(x)= x sinx is expanded as Fourier series in(-2,2),find a0
8. Find the half rangecosine series of f(x)={{π
9 State Raabe’s test
10 find eigen values of the matrix
−
π
<�<
π
<�<�
}
−
PART B: Analytical/Problem solving DESCRIPTIVE questions
Answer all questions (Each Question carries 15 marks)
11 a (i)If the centre of curvature of
the eccentricity is
√
+ =1 at one end of minor axis lies at the other end, prove
a (ii) Examinethe maxima and minima of f(x,y)=y2+4xy+3x2+x3
OR
12 b (i) If u = sin (
−
−
, then show that x
∂
∂
+y
∂
= 2 tanu
∂
b (ii) Show that the rectangular solid of maximum volume that can be inscribed in a sphere is a
cube.
13.a (i)Test the convergence of the seriesx −
√
+
√
- +………..
√
a (ii)Find the power series expansion of log(cos x) as far as and including the term containing x 4
OR
14 b (i)If y=⌈x + √x − ⌉m Prove that x −
yn+2+(2n+1)xyn+1+(n2-m2)yn= 0
2n−2
b (ii)Examine the convergence of the series ∑∞=
15a (i) Diagonalise the matrix
−
16b (i) For what values of and
+
−
√
OR
do the system of equations x+y+z=6,x+2y+ z= , x +2y+3z=10
have i no solution, ii unique solution iii more than one solution
b (ii)Given that A=
−
equal to the Trace A and
−
Verify that the sum and product of
the eigen values of A are
lAl respectively
17a (i) Obtain the first three coefficients in the Fourier cosine series for y, where y is given in the
following table
X 0 1 2 3 4 5
Y 3 9 6 8 2 7
OR
18 b (i) Obtain the Fourier cosine series of f(x)=e
x∈ [ , π]
b (ii) Express the function f(x)=x when -1<x<1 as a Fourier series with interval 2
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
Scanned by CamScanner
© Copyright 2025