Rolling Shutter Stereo - CVG
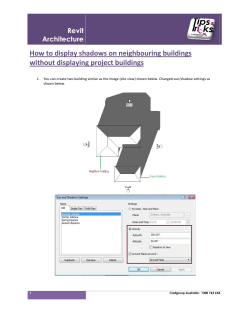
Rolling Shutter Stereo Olivier Saurer, Kevin Köser, Jean-Yves Bouguet, Marc Pollefeys ETH Zürich Switzerland GEOMAR Kiel Germany Google Inc, Mountain View, CA ETH Zürich Switzerland Motivation • Rolling Shutter Direction Most CMOS chips have an electronic rolling shutter Sequential exposure of scanline (rolling shutter) Cheap & Compact Light sensitive Resolution Rolling Shutter Time [ms] 2 1920 x 1080 26.04 2 1920 x 1080 32.67 iPhone 4S Galaxy S3 2 Oth et al. 2013 2 When to Consider Rolling Shutter (RS)? • RS distortion depends on: • Motion & Depth • Moving car: • Velocity = 25 km / h • RS distortion is measurable up to: 125m • Human motion: • Velocity = 5 km / h • RS distortion is measurable up to: 25m 3 Related Work Rolling Shutter Calibration Geyer et al. 2005 Removing Rolling Shutter Wobble Baker et al. 2010 Forssén et al. 2010 Oth et al. 2013 Rolling Shutter Structure from Motion Dense 3D Reconstruction ? Hedborg et al. 2010 Klingner et al. 2013 4 Outline Rolling Shutter 2-View Geometry Rolling Shutter Stereo (Proposed Method) Evaluation 5 Case 1: Valid Epipolar Geometry Left RS camera RS direction Right RS camera Camera motion direction 6 Case 1: Valid Epipolar Geometry Important special case: “Streetview” • Intra & inter baseline coincide Inter baseline Left RS camera RS direction Intra baselines Right RS camera Camera motion direction 7 Case 1: Valid Epipolar Geometry Important special case: “Streetview” • Intra & inter baseline coincide • Valid epipolar geometry Epipolar line P Inter baseline Left RS camera RS direction Intra baselines Right RS camera Camera motion direction 8 Case 1: Valid Epipolar Geometry Important special case: “Streetview” • Intra & inter baseline coincide • Valid epipolar geometry Epipolar line P Inter baseline Left RS camera RS direction Intra baselines Right RS camera Camera motion direction 9 Case 1: Valid Epipolar Geometry Important special case: “Streetview” • Intra & inter baseline coincide • Valid epipolar geometry Correct pixel correspondence Epipolar line P Inter baseline Left RS camera RS direction Intra baselines Right RS camera Camera motion direction 10 Case 1: Valid Epipolar Geometry Important special case: “Streetview” GS Epipolar line • Intra & inter baseline coincide • Valid epipolar geometry Correct pixel correspondence • Global Shutter triangulated 3D point P Inter baseline Left RS camera RS direction Intra baselines Right RS camera Camera motion direction 11 Case 1: Valid Epipolar Geometry RS GS P Inter baseline Left RS camera RS direction Intra baselines Important special case: “Streetview” • Intra & inter baseline coincide • Valid epipolar geometry Correct pixel correspondence GS triangulated 3D points have Epipolar line wrong depth RS triangulated 3D points have correct depth, considering correct pose at time of exposure Right RS camera Camera motion direction 12 Standard Stereo vs. RS Stereo RS & Camera Motion RS direction Input Images Camera motion direction Standard Proposed Stereo Method Ground Truth (RS Stereo) 13 1 Case 2: In General no Epipolar Geometry! • Intra & inter baseline do not coincide Left RS camera Right RS camera Standard Stereo: Proposed Method Only random matches 1Besides very special configurations [Seitz 2001, Pajdla 2001] 14 Outline Rolling Shutter 2-View Geometry Rolling Shutter Stereo (Proposed Method) Evaluation 15 Rolling Shutter Stereo - Idea • Solve simultaneously for depth & time of exposure P P’ Left RS camera RS direction Camera motion direction 16 Rolling Shutter Stereo - Idea • Solve simultaneously for depth & time of exposure 1. Sample 3D planes1 P P’ Left RS camera RS direction Camera motion direction 1Plane Sweep: [Collins 1996], [Yang et al. 2003] 17 Rolling Shutter Stereo - Idea • Solve simultaneously for depth & time of exposure 1. Sample 3D planes1 2. Given: • 3D Point • Camera trajectory Solve for time of exposure using RS projection model P P’ Left RS camera RS direction Camera motion direction 1Plane Sweep: [Collins 1996], [Yang et al. 2003] 18 Rolling Shutter Stereo - Idea • Solve simultaneously for depth & time of exposure P 1. Sample 3D planes1 2. Given: • 3D Point • Camera trajectory Solve for time of exposure using RS projection model 3. Texture lookup using time of exposure P’ Left RS camera RS direction Camera motion direction 1Plane Sweep: [Collins 1996], [Yang et al. 2003] 19 Rolling Shutter Stereo - Idea • Solve simultaneously for depth & time of exposure P Left RS camera RS direction P’ 1. Sample 3D planes1 2. Given: • 3D Point • Camera trajectory Solve for time of exposure using RS projection model 3. Texture lookup using time of exposure 4. Find best correlation1 P’’ Correlate Camera motion direction 1Plane Sweep: [Collins 1996], [Yang et al. 2003] 20 Rolling Shutter Stereo - Idea • Solve simultaneously for depth & time of exposure P Left RS camera RS direction P’ 1. Sample 3D planes1 2. Given: • 3D Point • Camera trajectory Solve for time of exposure using RS projection model 3. Texture lookup using time of exposure 4. Find best correlation1 P’’ Correlate Camera motion direction 1Plane Sweep: [Collins 1996], [Yang et al. 2003] 21 Rolling Shutter Projection • RS projection matrix changes with time : ? RS camera RS direction Camera motion direction 22 Rolling Shutter Projection • RS projection matrix changes with time • Find time of exposure when Solve fix-point function: : is seen. RS camera Quadratic polynomial1 RS direction Camera motion direction ? Projection of: RS image sensor 1Assuming Linear motion [Geyer et al. 2005] 23 Rolling Shutter Projection • RS projection matrix changes with time • Find time of exposure when Solve fix-point function: : ? is seen. RS camera Quadratic polynomial1 Projection of: • Valid solution: RS direction Camera motion direction RS image sensor 1Assuming Linear motion [Geyer et al. 2005] 24 RS Projection (With Lens Distortion) • Find time of exposure when Solve fix-point function: is seen. Polynomial of degree 8 Lens distortion Projection of: RS direction Camera motion direction RS image sensor 25 RS Projection (With Lens Distortion) • Find time of exposure when Solve fix-point function: is seen. Polynomial of degree 8 Lens distortion • Global undistortion does not help Projection of: Polynomial of degree 8 RS direction Camera motion direction RS image sensor 26 Motion Models • Further motion models are discussed in the paper Translation Orientation (# coefficient) Polynomial Degree Linear / Orbital / Spiral Const / Linear / Linear 0 2 Linear / Orbital / Spiral Const / Linear / Linear 1 4 Linear Linear Linear 1 5 5 5 8 9 Linear Const Linear Distortion 27 Outline Rolling Shutter 2 View Geometry Rolling Shutter Stereo (Proposed Method) Evaluation 28 Rolling Shutter Warp RS Warp Fast Approximation (FA) 1. 1. RS warp at grid vertices Left image 2. Right image Solve 8 degree polynomial Image size: 976 x 732 Speed: 27.7ms / warp (CUDA) Interpolate 2. Interpolate texture coordinates within grid cell Grid size: 1/10 of image size Speed: 2.2 ms / warp (CUDA) 29 Rolling Shutter Warp RS Warp Fast Approximation (FA) 1. 1. RS warp at grid vertices ~6 Left image 2. Hz with FA, with 50 planes Right image Solve 8 degree polynomial Image size: 976 x 732 Speed: 27.7ms / warp (CUDA) Interpolate 2. Interpolate texture coordinates within grid cell Grid size: 1/10 of image size Speed: 2.2 ms / warp (CUDA) 30 Results – Rendered Ground Truth Intra baseline Castle RS & Motion Old Town RS & Motion Intra baseline Ground Truth (LiDAR) Standard Stereo RS Stereo FA 31 Results Standard Stereo vs. RS Stereo RS & Motion Bird’s eye views Driving Speed: 25km/h Inter baseline: 2m Intra baseline: 0.5m Standard Stereo reconstruction & fusion RS reconstruction & fusion 32 Conclusion • RS hurts 3D reconstruction if ignored! • Radial distortion is depth dependent and can’t be undone without depth. • With little additional computational cost, similar quality RS 3D reconstruction is possible as with GS images. 33 Olivier Saurer, Kevin Köser, Jean-Yves Bouguet, Marc Pollefeys Thank you! Supported by Reconstruction from RS Streetview Images 35
© Copyright 2026