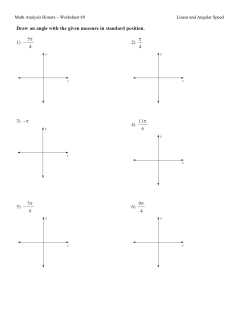1. No category

PROBLEM 15.112
The 18-in.-radius flywheel is rigidly attached to a 1.5-in. -radius
shaft that can roll along parallel rails. Knowing that at the instant
shown the center of the shaft has a velocity of 1.2 in./s and
an acceleration of 0.5 in./s 2 , both directed down to the left,
determine the acceleration (a) of Point A, (b) of Point B.
SOLUTION
Velocity analysis.
Let Point G be the center of the shaft and Point C be the point of contact with the rails. Point C is the
instantaneous center of the wheel and shaft since that point does not slip on the rails.
vG = rω , ω =
vG 1.2
=
= 0.8 rad/s
r 1.5
Acceleration analysis.
Since the shaft does not slip on the rails,
aC = aC
20°
aG = [0.5 in./s 2
Also,
20°]
aC = aG + (aC/G )t + (aC/G )n
[aC
Components
(a)
20°] = [0.5 in./s 2
20°:
0.5 = −1.5α
20°] + [1.5α
20°] + [1.5ω 2
20°]
α = 0.33333 rad/s 2
Acceleration of Point A.
aA = aG + (aA/G )t + (aA/G ) n
= [0.5
(b)
20°] + [18α
] + [18ω 2 ]
= [0.4698
] + [0.1710 ] + [6
= [6.4698
] + [11.670 ]
] + [11.52 ]
a A = 13.35 in./s 2
61.0° 
a B = 12.62 in./s 2
64.0° 
Acceleration of Point B.
a B = aG + (a B/G )t + (a B/G ) n
= [0.5
20°] + [18α
] + [18ω 2 ]
= [0.4698
] + [0.1710 ] + [6
= [5.5302
] + [11.349 ]
] + [11.52 ]
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1151
PROBLEM 15.121
Knowing that crank AB rotates about Point A with a constant angular velocity of
900 rpm clockwise, determine the acceleration of the piston P when θ = 120°.
SOLUTION
sin β sin120°
=
,
0.05
0.15
Law of sines.
β = 16.779°
ω AB = 900 rpm = 30π rad/s
Velocity analysis.
v B = 0.05ω AB = 1.5π m/s
v D = vD
60°
ωBD = ωBD
v D/B = 0.15ωBD
β
v D = v B + v D/B
[vD ] = [1.5π
Components
:
β]
0 = −1.5π cos 60° − 0.15ω BD cos β
ωBD = −
Acceleration analysis.
60°] + [0.15ωBD
1.5π cos 60°
= 16.4065 rad/s
0.15 cos β
α AB = 0
2
a B = 0.05ω AB
= (0.05)(30π )2 = 444.13 m/s 2
a D = aD
30°
α BD = α BD
a D/B = [0.15α AB
= [6α BD
2
β ] + [0.15ω BD
β ] + [40.376
a D = a B + a D/B
β]
β]
Resolve into components.
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1167
PROBLEM 15.121 (Continued)
:
0 = −444.13 cos 30° + 0.15α BD cos β + 40.376 sin β
α BD = 2597.0 rad/s 2
:
aD = −444.13 sin 30° − (0.15)(2597.0)sin β + 40.376 cos β
= −296 m/s 2
aP = aD
a P = 296 m/s 2 
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1168
PROBLEM 15.127
Knowing that at the instant shown rod AB has a constant angular
velocity of 6 rad/s clockwise, determine the acceleration of
Point D.
SOLUTION
ω AB = 6 rad/s
Velocity analysis.
v B = ( AB)ω AB
= (90)(6)
= 540 mm/s
v B = vB
, v D = vD
The instantaneous center of bar BDE lies at ∞.
ωBD = 0 and vD = vB = 540 mm/s
Then
ωCD =
vD 540
=
= 3 rad/s
CD 180
α AB = 0
Acceleration analysis.
2
a B = ( AB)ω AB
= [(90)(6)2 ] = 3240 mm/s 2
a D = [(CD)α CD
2
] + [(CD )ωCD
] = [180 α CD
= [180α CD
] + [1620 mm/s 2 ]
a D/B = [90α BD
2
] + [225α BD ] + [225ωBD
= [90α BD


Resolve into components.
−1620 = − 3240 + 225α BD ,
:
α BD = 7.2 rad/s 2
180α CD = 0 + (90)(7.2),
a D = [3240 ] + [(90)(7.2)
= [648
2
] + [90 ωBD
]
] + [225α BD ]
a D = a B + a D/B
:
] + [(180)(3) 2 ]
α CD = 3.6 rad/s 2
] + [(225)(7.2) ]
] + [1620 mm/s 2 ]
= 1745 mm/s 2
68.2°
a D = 1.745 m/s 2
68.2° 
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1179
PROBLEM 15.150
Pin P is attached to the collar shown; the motion of the pin is guided
by a slot cut in rod BD and by the collar that slides on rod AE.
Knowing that at the instant considered the rods rotate clockwise with
constant angular velocities, determine for the given data the velocity
of pin P.
ω AE = 8 rad/s, ωBD = 3 rad/s
SOLUTION
AB = 500 mm = 0.5 m, AP = 0.5 tan 30°, BP =
ω AE = 8 rad/s
0.5
cos 30°
ω BD = 3 rad/s
,
Let P′ be the coinciding point on AE and u1 be the outward velocity of the collar along the rod AE.
v P = v P′ + v P/ AE = [( AP)ω AE ] + [u1
]
Let P′′ be the coinciding point on BD and u2 be the outward speed along the slot in rod BD.
v P = v P′′ + v P/BD = [( BP)ωBD
30°] + [u2
60°]
Equate the two expressions for v P and resolve into components.
:
u1 = 1.5 + 0.5u2
or
:
u2 =
From (1),
 0.5 
u1 = 
 (3)(cos30°) + u2 cos 60°
 cos30° 
(1)
 0.5 
−(0.5 tan 30°)(8) = − 
 (3)sin 30° + u2 sin 60°
 cos30° 
1
[1.5 tan 30° − 4 tan 30°] = −1.66667 m/s
sin 60°
u1 = 1.5 + (0.5)(−1.66667) = 0.66667 m/s
v P = [(0.5 tan 30°)(8) ] + [0.66667
] = [2.3094 m/s ] + [0.66667 m/s
]
vP = − 2.30942 + 0.66667 2 = 2.4037 m/s
tanβ =
2.3094
0.66667
β = 73.9°
v P = 2.40 m/s
73.9° 
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1212
PROBLEM 15.163
The motion of blade D is controlled by the robot arm ABC. At the instant
shown, the arm is rotating clockwise at the constant rate ω = 1.8 rad/s and
the length of portion BC of the arm is being decreased at the constant rate
of 250 mm/s. Determine (a) the velocity of D, (b) the acceleration of D.
SOLUTION
i =1
Unit vectors:
Units: meters, m/s, m/s
, j =1 ,
k=
2
rD /A = (0.32 m)i − (0.24 m) j
Motion of Point D′ of extended frame AB.
ω = −(1.8 rad/s)k
α=0
v D′ = ω × rD /A = ( −1.8k ) × (0.32i − 0.24 j)
= −0.432i − 0.576 j
a D′ = α × rD /A − ω 2 (rD /A )
= 0 − (1.8)2 (0.32i − 0.24 j)
= −1.0368i + 0.7776 j
Motion of Point D relative to frame AB.
v D /AB = 250 mm/s
25°
= −(0.25cos 25°)i + (0.25sin 25°) j
= −0.22658i + 0.10565 j
a D /AB = 0
Coriolis acceleration
2ω × v D /AB = (2)(−1.8k ) × (−0.22658i + 0.10565 j)
= 0.38034i + 0.81569 j
(a)
Velocity of Point D.
v D = v D′ + v D /AB
= −0.432i − 0.576 j − 0.22658i + 0.10565 j
= −0.65858i − 0.47035 j
v D = (0.659 m/s)i − (0.470 m/s) j = 0.809 m/s
35.5° 
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1227
PROBLEM 15.163 (Continued)
(b)
Acceleration of Point D.
a D = a D′ + a D /AB + 2ω × v D /AB
= −1.0368i + 0.7776 j + 0 + 0.38034i + 0.81569 j
= −0.6565i + 1.5933 j
a D = −(0.657 m/s 2 )i + (1.593 m/s 2 ) j = 1.723 m/s 2
67.6° 
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1228
PROBLEM 15.168
A chain is looped around two gears of radius 40 mm that can
rotate freely with respect to the 320-mm arm AB. The chain
moves about arm AB in a clockwise direction at the constant
rate of 80 mm/s relative to the arm. Knowing that in the
position shown arm AB rotates clockwise about A at the
constant rate ω = 0.75 rad/s, determine the acceleration of
each of the chain links indicated.
Links 1 and 2.
SOLUTION
Let the arm AB be a rotating frame of reference.
Link 1:
Ω = 0.75 rad/s
= −(0.75 rad/s)k :
r1 = −(40 mm)i, v1/AB = u ↑ = (80 mm/s) j
a1′ = −Ω 2 r1 = −(0.75)2 ( −40) = (22.5 mm/s)i
802
160 mm/s → = (160 mm/s 2 )i
40
ρ
= (2)( −0.75k ) × (80 j)
a1/AB =
2Ω × v P /AB
u2
=
= (120 mm/s)i
a1 = a1′ + a1/AB + 2Ω × v1/AB
= (302.5 mm/s 2 )i
Link 2:
a1 = 303 mm/s 2

r2 = (160 mm)i + (40 mm) j
v 2/AB = u → = (80 mm/s)i
a′2 = −Ω 2 r2
= −(0.75)2 (160i + 40 j)
a 2/AB
= −(90 mm/s 2 )i − (22.5 mm/s 2 ) j
=0
2Ω × v 2/AB = (2)(−0.75k ) × (80i)
= −(120 mm/s 2 ) j
a 2 = a′2 + a 2/AB + 2Ω × v 2/AB
= −90i − 22.5 j − 120 j
= −(90 mm/s 2 )i − (142.5 mm/s 2 ) j
a 2 = (90) 2 + (142.5) 2
= 168.5 mm/s 2
tan β =
142.5
, β = 57.7°
90
a 2 = 168.5 mm/s 2
57.7° 
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
1235