1. finance

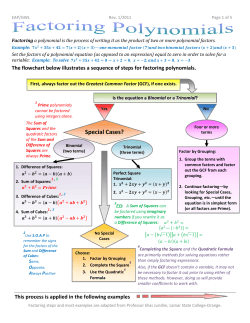
Section P.6
P.6
Factoring Trinomials
61
Factoring Trinomials
What you should learn:
• Factor trinomials of the form
x2 bx c
• Factor trinomials of the form
ax2 bx c
• Factor trinomials by grouping
• Factor perfect square trinomials
• Select the best factoring
technique using the guidelines
for factoring polynomials
Why you should learn it:
The techniques for factoring
trinomials will help you in solving
quadratic equations.
Factoring Trinomials of the Form x2 bx c
Try covering the factored forms in the left-hand column below. Can you determine the factored forms from the trinomial forms?
Factored Form
F
O
I
L
Trinomial Form
x 1x 4 4x x 4 x2 3x 4
x 3x 2 x2 2x 3x 6 x2 5x 6
3x 5x 1 3x2 3x 5x 5 3x2 8x 5
x2
Your goal here is to factor trinomials of the form x2 bx c. To begin, consider
the factorization
x2 bx c x mx n.
By multiplying the right-hand side, you obtain the following result.
x mx n x2 nx mx mn
x2 m nx mn
Sum of
terms
x2 Product of
terms
b x
c
So, to factor a trinomial x2 bx c into a product of two binomials, you must
find two factors of c with a sum of b.
Example 1 Factoring Trinomials
Study Tip
Use a list to help you find the
two numbers with the required
product and sum. For Example
1(a):
Factors of 8
Sum
1, 8
7
1, 8
7
2, 4
2
2, 4
2
Because 2 is the required
sum, the correct factorization is
x2 2x 8 x 4x 2.
Factor the trinomials (a) x2 2x 8 and (b) x2 5x 6.
Solution
(a) You need to find two factors whose product is 8 and whose sum is 2.
The product of 4 and 2 is 8.
x2 2x 8 x 4x 2
The sum of 4 and 2 is 2.
(b) You need to find two factors whose product is 6 and whose sum is 5.
The product of 3 and 2 is 6
x2 5x 6 x 3x 2
The sum of 3 and 2 is 5.
Now try Exercise 7.
Note that when the constant term of the trinomial is positive, its factors must
have like signs; otherwise, its factors have unlike signs.
62
Chapter P
Prerequisites
Factors of 24
Sum of Factors
124
124
212
212
38
38
46
46
1 24 23
1 24 23
2 12 10
2 12 10
3 8 5
3 8 5
4 6 2
4 6 2
Study Tip
With any factoring problem,
remember that you can check
your result by multiplying. For
instance, in Example 2, you can
check the result by multiplying
x 9 by x 2 to see that
you obtain x2 7x 18.
Remember that not all
trinomials are factorable
using integers. For instance,
x2 2x 4 is not factorable
using integers because there is
no pair of factors of 4 whose
sum is 2.
When factoring a trinomial of the form x2 bx c, if you have trouble
finding two factors of c with a sum of b, it may be helpful to list all of the distinct
pairs of factors and then choose the appropriate pair from the list. For instance,
consider the trinomial
x2 5x 24.
For this trinomial, c 24 and b 5. So, you need to find two factors of
24 with a sum of 5, as shown at the left. With experience, you will be
able to narrow this list down mentally to only two or three possibilities whose
sums can then be tested to determine the correct factorization, which is
x2 5x 24 x 3x 8.
Example 2 Factoring a Trinomial
Factor the trinomial x2 7x 18.
Solution
To factor this trinomial, you need to find two factors whose product is 18 and
whose sum is 7.
The product of 2 and 9 is 18.
x2
7x 18 x 2x 9
The sum of 2 and 9 is 7.
Now try Exercise 11.
Applications of algebra sometimes involve trinomials that have a common
monomial factor. To factor such trinomials completely, first factor out the
common monomial factor. Then try to factor the resulting trinomial by the
methods given in this section.
Example 3 Factoring Completely
Factor the trinomials (a) 4x3 8x2 60x and (b) 5x2y 20xy2 15y3
completely.
Solution
(a) This trinomial has a common monomial factor of 4x. So, you should start the
factoring process by factoring 4x out of each term.
4x3 8x2 60x 4xx2 2x 15
4xx x 4xx 3x 5
Factor out common
monomial factor.
Think: You need two factors
of 15 with a sum of 2.
35 15,
3 5 2
(b) This trinomial has a common monomial factor of 5y. So, you should start the
factoring process by factoring 5y out of each term.
5yx x Factor out common
monomial factor.
Think: You need two factors of 3 with a sum of 4.
5yx yx 3y
13 3, 1 3 4
5x2y 20xy2 15y3 5yx2 4xy 3y2
Now try Exercise 19.
Section P.6
Factoring Trinomials
63
Factoring Trinomials of the Form ax2 bx c
To factor a trinomial whose leading coefficient is not 1, use the following pattern.
Factors of a
ax2 bx c x x Factors of c
The goal is to find a combination of factors of a and c such that the outer and
inner products add up to the middle term bx. For instance, in the trinomial
6x2 17x 5, a 6, c 5, and b 17. After some experimentation, you can
determine that the factorization is
6x2 17x 5 2x 53x 1.
Example 4 Factoring a Trinomial of the Form ax2 bx c
Factor the trinomial 6x2 5x 4.
Solution
First, observe that 6x2 5x 4 has no common monomial factor. For this
trinomial, you have ax2 bx c 6x2 5x 4, which implies that a 6,
c 4, and b 5. The possible factors of the leading coefficient 6 are 16
and 23, and the possible factors of 4 are 14, 14, and 22. By
trying the many different combinations of these factors, you obtain the following
list.
Study Tip
If the original trinomial has no
common monomial factor, its
binomial factors cannot have
common monomial factors. So,
in Example 4, you do not have
to test factors, such as 6x 4,
that have a common factor of 2.
Which of the other factors in
Example 4 did not need to be
tested?
x 16x 4 6x2 2x 4
x 16x 4 6x2 2x 4
x 46x 1 6x2 23x 4
x 46x 1 6x2 23x 4
x 26x 2 6x2 10x 4
x 26x 2 6x2 10x 4
2x 13x 4 6x2 5x 4
2x 13x 4 6x2 5x 4
2x 43x 1 6x2 10x 4
2x 43x 1 6x2 10x 4
2x 23x 2 6x2 2x 4
2x 23x 2 6x2 2x 4
Correct factorization
So, you can conclude that the correct factorization is
6x2 5x 4 2x 13x 4.
Check this result by multiplying 2x 1 by 3x 4.
Now try Exercise 33.
64
Chapter P
Prerequisites
To help shorten the list of possible factorizations of a trinomial of the form
ax2 bx c, use the guidelines presented below.
Guidelines for Limiting Possible Trinomial Factorizations
1. If the trinomial has a common monomial factor, you should factor out the
monomial factor before trying to find binomial factors. For instance, the
trinomial 12x2 10x 8 has a common factor of 2. By removing this
common factor, you obtain 12x2 10x 8 26x2 5x 4.
2. Do not switch the signs of the factors of c unless the middle term is correct except in sign. In Example 4, after determining that x 46x 1
is not the correct factorization, for instance, it is unnecessary to test
x 46x 1.
3. Do not use binomial factors that have a common monomial factor. Such a
factor cannot be correct, because the trinomial has no common monomial
factor. (Any common monomial factor should already have been factored
out, in accordance with Guideline 1.) For instance, in Example 4, it is
unnecessary to test x 16x 4 6x2 2x 4 because the factor
6x 4 has a common factor of 2.
Using these guidelines, you could shorten the list given in Example 4 to the
following three possible factorizations.
x 46x 1 6x2 23x 4
2x 13x 4 6x2 5x 4
2x 13x 4 6x2 5x 4
Correct factorization
Do you see why you can cut the list from 12 possible factorizations to only three?
Example 5 Factoring a Trinomial of the Form ax2 bx c
Factor the trinomial 2x2 x 21.
Solution
First observe that 2x2 x 21 has no common monomial factor. For this
trinomial, a 2, which factors as 12, and c 21, which factors as
121, 121, 37, or 73.
2x 1x 21 2x2 41x 21
2x 21x 1 2x2 19x 21
2x 3x 7 2x2 11x 21
2x 7x 3 2x2 x 21
2x 7x 3 2x2 x 21
Middle term has incorrect sign.
Correct factorization
So, the correct factorization of
x 21 is 2x 7x 3. Check this
result by multiplying 2x 7 by x 3.
2x2
Now try Exercise 35.
Remember that if the middle term is correct except in sign, you need only change
the signs of the factors of c, as in Example 5.
Section P.6
Factoring Trinomials
65
Example 6 Factoring Trinomials
Factor the trinomials (a) 3x2 11x 10 and (b) 5x2 9xy 4y2.
Solution
(a) First, observe that 3x2 11x 10 has no common monomial factor. For this
trinomial, a 3, which factors as 13, and c 10, which factors as
110 or 25. You can test the possible factors as follows.
x 103x 1 3x2 31x 10
x 13x 10 3x2 13x 10
x 53x 2 3x2 17x 10
x 23x 5 3x2 11x 10
Correct factorization
So, the correct factorization is
3x2 11x 10 x 23x 5.
(b) First observe that 5x2 9xy 4y2 has no common monomial factor. For this
trinomial, a 5, which factors as 15, and c 4, which factors as 14
or 22. You can test the possible factors as follows.
x 4y5x y 5x2 21xy 4y2
x y5x 4y 5x2 9xy 4y2
Correct factorization
So, the correct factorization is
5x2 9xy 4y2 x y5x 4y.
Now try Exercise 37.
Remember that if a trinomial has a common monomial factor, the common
monomial factor should be removed first. This is illustrated in the next two
examples.
Example 7 Factoring Completely
Factor 8x2 y 60xy 28y completely.
Solution
Begin by factoring out the common monomial factor 4y.
8x2 y 60xy 28y 4y2x2 15x 7
Now, for the new trinomial 2x2 15x 7, a 2 and c 7. The possible
factorizations of this trinomial are as follows.
2x 7x 1 2x2 9x 7
2x 1x 7 2x2 15x 7
Correct factorization
So, the complete factorization of the original trinomial is
8x2 y 60xy 28y 4y2x2 15x 7
4y2x 1x 7.
Now try Exercise 49.
66
Chapter P
Prerequisites
Example 8 Factoring Completely
Factor 4x4 2x3y 6x2y2 completely.
Solution
Begin by factoring out the common monomial factor 2x2.
4x4 2x3y 6x2y2 2x22x2 xy 3y2
Now, for the new trinomial 2x2 xy 3y2, a 2, and c 3. The possible
factorizations of this trinomial are as follows.
Study Tip
When factoring a trinomial with
a negative leading coefficient,
first factor 1 out of the trinomial, as demonstrated in
Example 9.
2x yx 3y 2x2 5xy 3y2
2x 3yx y 2x2 xy 3y2
2x 3yx y 2x2 xy 3y2
Transpose lines.
Middle term has incorrect sign.
Correct factorization
So, the complete factorization of the original trinomial is
4x 4 2x3y 6x2y2 2x22x2 xy 3y2
2x22x 3yx y.
Now try Exercise 51.
Example 9 A Trinomial with a Negative Leading Coefficient
Factor the trinomial 3x2 16x 35.
Solution
This trinomial has a negative leading coefficient, so you should begin by factoring
1 out of the trinomial.
3x2 16x 35 13x2 16x 35
Now, for the new trinomial 3x2 16x 35, you have a 3 and c 35. The
possible factorizations of this trinomial are as follows.
3x 1x 35 3x2 104x 35
3x 35x 1 3x2 32x 35
3x 5x 7 3x2 16x 35
3x 5x 7 3x2 16x 35
Middle term has incorrect sign.
Correct factorization
So, the correct factorization is
3x2 16x 35 13x 5x 7.
Alternative forms of this factorization include
3x 5x 7 and 3x 5x 7.
Now try Exercise 53.
Not all trinomials are factorable using only integers. For instance, to factor
x2 3x 5
you need factors of 5 that add up to 3. This is not possible, because the only
integer factors of 5 are 1 and 5, and their sum is not 3. Such a trinomial is not
factorable over the integers. Polynomials that cannot be factored using integer
coefficients are called prime with respect to the integers. Some other examples
of prime polynomials are 2x2 3x 2, 4x2 9, and 2x2 xy 7y2. Watch for
other trinomials that are not factorable in the exercises for this section.
Section P.6
Factoring Trinomials
67
Factoring Trinomials by Grouping (Optional)
In this section, you have seen that factoring a trinomial can involve quite a bit of
trial and error. An alternative technique that some people like to use is factoring
by grouping. For instance, suppose you rewrite the trinomial 2x2 x 15 as
2x2 x 15 2x2 6x 5x 15.
Then, by grouping the first and second terms and the third and fourth terms, you
can factor the polynomial as follows.
2x2 x 15 2x2 6x 5x 15
2x2
6x 5x 15
2xx 3 5x 3
x 32x 5
Rewrite middle term.
Group terms.
Factor out common monomial
factor in each group.
Distributive Property
The key to this method of factoring is knowing how to rewrite the middle term.
In general, to factor a trinomial ax2 bx c by grouping, choose factors of the
product ac that add up to b and use these factors to rewrite the middle term. This
technique is illustrated in Example 10.
Study Tip
You should put a polynomial in
standard form before trying to
factor by grouping. Then group
and remove a common monomial factor from the first two terms
and the last two terms. Finally,
if possible, factor out the common binomial factor.
Example 10 Factoring a Trinomial by Grouping
Use factoring by grouping to factor the trinomials completely.
(a) 2x2 5x 3
(b) 6y2 5y 4
Solution
(a) In the trinomial 2x2 5x 3, a 2 and c 3, which implies that the
product ac is 6. Now, because 6 factors as 61, and 6 1 5 b,
you can rewrite the middle term as 5x 6x x. This produces the following result.
2x2 5x 3 2x2 6x x 3
2x2
6x x 3
2xx 3 x 3
x 32x 1
Rewrite middle term.
Group terms.
Factor out common monomial
factor in first group.
Distributive Property
So, the trinomial factors as 2x2 5x 3 x 32x 1.
(b) In the trinomial 6y2 5y 4, a 6 and c 4, which implies that the
product of ac is 24. Now, because 24 factors as 83, and
8 3 5 b, you can rewrite the middle term as 5y 8y 3y. This produces the following result.
6y2 5y 4 6y2 8y 3y 4
6y2
8y 3y 4
2y3y 4 3y 4
3y 42y 1
Rewrite middle term.
Group terms.
Factor out common monomial
factor in first group.
Distributive Property
So, the trinomial factors as 6y2 5y 4 3y 42y 1.
Now try Exercise 59.
68
Chapter P
Prerequisites
Factoring Perfect Square Trinomials
A perfect square trinomial is the square of a binomial. For instance,
x2 6x 9 x 3x 3 x 32
is the square of the binomial x 3, and
4x2 20x 25 2x 52x 5 2x 52
is the square of the binomial 2x 5. Perfect square trinomials come in two
forms: one in which the middle term is positive, and the other in which the middle
term is negative.
Perfect Square Trinomials
Let u and v represent real numbers, variables, or algebraic expressions. Then
the perfect square trinomials below can be factored as indicated.
u2 2uv v2 u v2
u2 2uv v2 u v2
Like signs
Like signs
To recognize a perfect square trinomial, remember that the first and last
terms must be perfect squares and positive, and that the middle term must be
twice the product of u and v. (The middle term can be positive or negative.)
Example 11 Factoring Perfect Square Trinomials
Rewrite each trinomial as a perfect square trinomial. Then factor the trinomial.
(a) x2 4x 4
(b) 16y2 24y 9
(c) 9x2 30xy 25y2
Solution
(a) x2 4x 4 x2 2x2 22 x 22
(b) 16y2 24y 9 4y2 24y3 32 4y 32
(c) 9x2 30xy 25y2 3x2 23x5y 5y2 3x 5y2
Now try Exercise 63.
Example 12 Factoring out a Common Monomial Factor First
Factor out any common monomial factors from each trinomial. Then factor
completely.
(a) 3x2 30x 75
(b) 16y 3 80y 2 100y
Solution
(a) 3x2 30x 75 3x2 10x 25
3x 52
(b) 16y3 80y2 100y 4y4y2 20y 25
4y2y 52
Now try Exercise 83.
Factor out common
monomial factor.
Factor as perfect square trinomial.
Factor out common
monomial factor.
Factor as perfect square trinomial.
Section P.6
Factoring Trinomials
69
Summary of Factoring
Although the basic factoring techniques have been discussed one at a time, from
this point on you must decide which technique to apply to any given problem
situation. The guidelines below should assist you in this selection process.
Guidelines for Factoring Polynomials
1. Factor out any common factors.
2. Factor according to one of the special polynomial forms: difference
of squares, sum or difference of cubes, or perfect square trinomial.
3. Factor trinomials, ax2 bx c, using the methods for a 1 or a 1.
4. Factor by grouping—for polynomials with four terms.
5. Check to see if the factors themselves can be factored further.
6. Check the results by multiplying the factors.
Example 13 Factoring Polynomials
Factor each polynomial completely.
(a) 3x2 108
(b) 4x3 32x2 64x
(d) x3 3x2 4x 12
(c) 6x3 27x2 15x
(e) x2 6x 9 y2
Solution
(a) 3x2 108 3x2 36
Factor out common factor.
3x 6x 6
(b)
4x3
32x2
64x 4x
x2
Difference of two squares
8x 16
4xx 4
2
Perfect square trinomial
(c) 6x3 27x2 15x 3x2x2 9x 5
3x2x 1x 5
(d) x3 3x2 4x 12 x3 3x2 4x 12
x 3 4x 3
x 3x2 4
x 3x 2x 2
x2
(e) x2 6x 9 y2 x2 6x 9 y2
x 3 2
Factor out common factor.
y2
Factor out common factor.
Factor trinomial.
Group terms.
Factor out common factors.
Distributive Property
Difference of two squares
Group terms.
Perfect square trinomial
x 3 yx 3 y
Difference of two squares
x 3 yx 3 y
Simplify.
Now try Exercise 97.
Notice the grouping in the first step of Example 13(e). The first three terms
form a perfect square trinomial, which enables you to further factor the polynomial as the difference of two squares.
70
Chapter P
P.6
Prerequisites
Exercises
VOCABULARY CHECK: Fill in the blanks.
1. Polynomials that cannot be factored using integer coefficients are called ________.
2. If a polynomial has four terms, a method of factoring called ________ may be used.
3. A ________ is the square of a binomial.
In Exercises 1–6, fill in the missing factor.
1. x2 5x 4 x 4
43. 20x2 x 12
44. 10x2 9xy 9y2
45. 2u2 9uv 35v2
46. 5r 2 4rs 9s2
2. a2 2a 8 a 4
47. 15x2 3xy 8y2
48. 9u2 5uv 6v2
4. y2 6y 8 y 4
49. 6x2y 22xy 40y
50. 6a2b2 57ab2 27b2
51. 8x 4 6x3y 2x2y2
52. 24u3 54u2v 27uv2
3. y2 y 20 y 4
5. z2 6z 8 z 4
6. z2 2z 24 z 4
In Exercises 7–22, factor the trinomial.
7. x2 4x 3
8. x2 10x 24
9. y2 7y 30
10. m2 3m 10
11. t2 4t 21
12. x2 4x 12
13. x2 12x 20
14. y2 8y 33
15. t2 17t 60
17. x2 20x 96
16. z2 13z 36
19.
u2
5uv 6v2
21.
x2
2xy 35y2
In Exercises 53–56, factor the trinomial by first factoring
1 from each term.
7xy 20.
2
22. a 21ab 110b2
12y2
In Exercises 23–28, fill in the missing factor.
26.
5c2
11c 12 c 3
27. 2y2 3y 27 y 3
28. 3y2 y 30 y 3
In Exercises 29–52, factor the trinomial, if possible. Some of
the expressions are not factorable using integer coefficients.
31.
8t2
6t 5
33. 6b2 19b 7
30. 5x2 7x 2
32.
2x2
6x 2
37. 2x2 5xy 3y2
38. 5a2 8ab 3b2
39. 11y2 43yz 4z2
40. 6u2 7uv 5v2
41.
ab 42.
59. 6x2 x 2
60. 6x2 x 15
61. 15x2 11x 2
62. 12x2 28x 15
24x2
14xy a2
12a 36
66. y2 14y 49
68. 4z2 28z 49
69. 9b2 12b 4
70. 4x2 4x 1
71. 4x2 4xy y2
72. m2 6mn 9n2
73. u2 8uv 16v2
74. 4y2 20yz 25z2
In Exercises 75–112, completely factor the algebraic
expression.
77. 10t3 2t2 36t
3y2
64. z2 6z 9
67. 25y2 10y 1
76. 20y2 45
35. 2a2 13a 20
2b2
58. 2x2 9x 9
75. 3x5 12x3
34. 12a2 2a 4
36. 9t2 51t 30
6a2
57. 3x2 10x 8
65.
12a 9 a 3
29. 3x2 4x 1
56. 2 5x 12x2
63. x2 4x 4
24. 5x2 19x 12 x 3
25.
55. 1 11x 60x2
In Exercises 63–74, factor the perfect square trinomial.
23. 5x2 18x 9 x 3
5a2
54. 6x2 5x 6
In Exercises 57–62, factor the trinomial by grouping.
18. y2 22y 96
x2
53. 2x2 x 6
78. 3x2 12x 36
79. 5a2 25a 30
80. 4t2 8t 32
Section P.6
81. 6u2 3u 63
82.
10x2
83.
9y2
22x 24
In Exercises 119–124, find a real number c such that the
algebraic expression is a perfect square trinomial.
66y 121
119. x2 8x c
84. 16z2 56z 49
121. y2 6y c
85. 4x3x 2 3x 22
122. z2 20z c
86. 2x 52 x2x 5
123. 16a2 40a c
87. x2x 3 5xx 3
124. 9t2 12t c
88. 6y32y 5 3y22y 5
89. 36 z 32
90. x 42 25
91. 2y 12 9
92. 81 3t 22
71
Factoring Trinomials
120. x2 12x c
In Exercises 125 and 126, fill in the missing number.
125. x2 12x 50 x 62 126. x2 10x 22 x 52 93. 54x3 2
In Exercises 127–132, find all integers b such that the trinomial can be factored.
94. 3t3 24
127. x2 bx 18
95. v 3v 5v
3
2
10a
96.
97. 2x3y 2x2y2 84xy3
2a3
8a2
98. 8m3n 20m2n2 48mn3
99.
5x2y
20y3
100.
27a3
3ab2
101.
x3
2x2 16x 32
102. x3 7x2 4x 28
103. x3 6x2 9x 54
104. x3 10x2 16x 160
105. x2 10x 25 y2
106. 9y2 12y 4 z2
107. a2 2ab b2 16
128. x2 bx 14
129. x2 bx 21
130. x2 bx 7
131. 5x2 bx 8
132. 3x2 bx 10
In Exercises 133–138, find two integers c such that the
trinomial can be factored. (There are many correct answers.)
133. x2 6x c
134. x2 9x c
135. x2 3x c
136. x2 12x c
137. t2 4t c
108. x2 14xy 49y2 4a2
138. s2 s c
109. x8 1
Geometry
111. b4 216b
In Exercises 139–142, write, in factored form,
an expression for the area of the shaded portion of the
figure.
112. x4 16y4
139.
110. 3y3 192
x
116. 36z2 bz 1
117. 4x2 bx 9
118. 16x2 bxy 25y2
4
x
8 xx
x
x
x
113. x2 bx 81
115. 9y2 by 1
x
x
In Exercises 113–118, find two real numbers b such that the
algebraic expression is a perfect square trinomial.
114. x2 bx 16
140.
x
18
9
141.
142.
3
x
6
x+3
4
2x
5
5
(x
4
+ 3)
72
Chapter P
Prerequisites
143. Geometry A rectangle has area and width as
indicated in the figure. Factor to find the length.
(d)
a
a
b
b
2x − 5
A = 2x 2 + x − 15
1
1
?
1
1
b
144. Geometry A circle has area as indicated in the
figure. Factor to find the radius.
1
145. a2 b2 a ba b
146. a2 2ab b2 a b2
147. a2 2a 1 a 12
?
148. ab a b 1 a 1b 1
Area = π x 2 − 12 π x + 36π
Geometric Modeling
In Exercises 149 and 150, factor
the trinomial and represent the result with a geometric
factoring model.
Geometric Modeling In Exercises 145–148, match the
factoring formula with the correct geometric factoring
model. [ The models are labeled (a), (b), (c), and (d).]
(a)
a
a
a
1
149. x2 4x 3
Synthesis
151. Error Analysis
a
150. x2 5x 4
Identify the error.
9x2 9x 54 3x 63x 9
1
1
1
(b)
1
a
a
a
b
In Exercises 153 and 154, explain how the same
result could be obtained mentally using the sample below as
a model.
b
292 30 12 302 2301 12
b
b
152. Think About It Is xx 2 2x 2
completely factored? Explain.
Writing
a
b
900 60 1
b
a
(c)
3x 2x 3
1
a
841
b
153. 522 2704
a−b
a
154. 392 1521
155. (a) Completely factor the expression
b
b
4x3 36x2 80x.
(b) An open box is to be made from a rectangular
piece of material 10 inches long and 8 inches
wide by cutting equal squares of side x from
each corner and turning up the sides. Show that
the volume of the box can be described by the
factored expression in part (a).