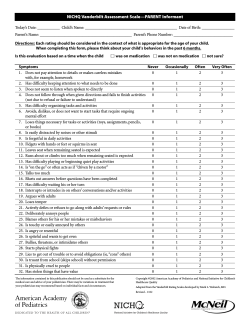
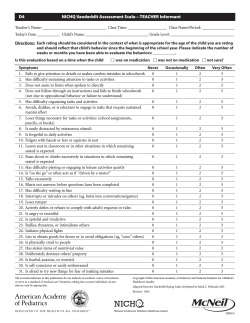
Objectives A How-to Guide for an Effective Journal Club Lisa Lundquist, PharmD, BCPS Clinical Assistant Professor Mercer University Atlanta, GA • • • • How to select an article to evaluate How to critically evaluate a study How to apply basic statistical concepts How to effectively deliver a journal club presentation Sabrina Cole, PharmD, BCPS Clinical Pharmacist Specialist, Drug Information Grady Health System Atlanta, GA Primary Literature • Original publications • Necessary for the development of secondary and tertiary literature resources • Study design, methodology, and scientific results included • Peer review process enhances validity of study and authors’ conclusions • Examples: research studies, case reports, editorials, letters-to-the-editor Major Goals of Interpretation • Establish the significance or importance of the trial • Relate the results to the original objectives of the trial • Compare data from the trial with data obtained from other trials 1 Common Problems Encountered in Literature • • • • • • • Flawed study design Invalid statistical analysis Fraud, deception, and misrepresentation Unintentional errors Poorly conducted research Poorly written manuscripts Data dredging Publication Process 1. 2. 3. 4. 5. Selection of journal Preparation for submission Review / peer review Revision Resubmission Peer Review Process Manuscript Editor Reviewer A Comments Reviewer B and suggestions Reviewer C Critical Literature Evaluation Accept Accept with revision Reject 2 Types of Studies • Prospective vs. retrospective – Prospective – followed forward into time – Retrospective – reviewed back in time Types of Studies • Descriptive vs Explanatory – Descriptive – serves to inform other healthcare professionals – Explanatory – determines if a difference exists between interventions • Observational • Experimental Types of Studies • Crossover – Experimental (interventional), prospective – Patient receives both the study and control medications separated during specified time periods A B • Parallel A B – Experimental (interventional), prospective – Patient receives either the study or control medication throughout the study A B Types of Studies • Cohort – Observational, prospective – Design may involve the evaluation of risk factors for disease development in a specified population • Case-control – Observational, retrospective – Patients with the disease (cases) and without the disease (controls) are compared to determine the exposure to the risk factor in question • Cross-sectional – study where measurements are taken at a single point in time 3 Types of Studies Types of Studies • Clinical – any experiment in which a drug is administered or dispensed to one or more human subjects • Quality of life – evaluation of a patient’s living situation based on the patient’s environment, family life, financial situation, educations, and health • N-of-1 – controlled study conducted in a single subject where periods of exposure to a treatment are compared to periods of exposure to placebo • Post-marketing surveillance – study designed to examine drug use and frequency of side effects following approval by FDA • Stability – study designed to determine the stability of drugs in various preparations • Meta-analysis – type of review where conclusions are based on the summarization of results obtained from combining and statistically evaluating data from previously conducted studies • Bioequivalence – research that evaluates whether products are similar in rate and extent of absorption Relative Strength of Causal Relationships Based on Study Design Increasing Strength • • • • Randomized clinical trials Meta-analyses Follow-up (cohort) study Case-control (trohoc) study • Case series • Case reports • Pharmacoeconomic – study of economic impact of drug therapies or services Controls • Controls – a treatment used for comparison in a study – placebo control – historical control – cross-over control – standard-treatment control – within-patient comparison control 4 Randomization • Any one individual has a predetermined probability of being assigned to each particular study and control group • Decreases but does not eliminate the possibility that study and control groups will differ according to factors that affect prognosis Randomization • All inclusion and exclusion criteria must be met before randomization occurs • Types - Simple Block (cluster) Stratified Non-randomization Blinding • Rationale - To prevent clinicians from assessing/treating one patient group differently from the other - To overcome the “placebo effect” - To ensure equal patient compliance • Limitations Blinding • Types - Single-blind Double-blind Triple-blind Double-dummy - May be difficult to blind a medication with a distinctive taste, physiologic effect, or continuous titration - Expensive and time consuming 5 Bias • Components of the trial design which can influence the outcome(s) studied • Controlling for Bias - Minimize confounders Proper selection of patients Objective method(s) of selecting data Blinding Use a control group Reliable data sources Population and Samples • Population – Every individual in the universe with the specific characteristics or disease states under study • Sample – Group or individual chosen as representatives from the population under study Variables • Dependent variable – outcome of interest within the study • Independent variable – the intervention or what is being manipulated • Confounding variables – affect the patients’ conditions and are associated statistically with the intervention being evaluated – Example: • In studying whether cigarette smoking causes lung cancer in a case-control study, drinking alcohol would be a confounding factor because people who smoke cigarettes are more likely to drink alcohol. Validity • Internal validity – Within the confines of the study, the methods and analysis used stand up to scrutiny, the investigators’ interpretation is supported, and the results appear accurate • External validity – Generalizability. The ability to apply the information to the reader’s practice setting • NO internal validity = NO external validity 6 Analysis • Intention-to-treat – Compares outcome based on the intended initial subjects’ assignments – Determines the effect of treatment under usual conditions (eg, gives a better idea of how the drug will do in the real world) – No data should be eliminated Analysis • As-treated – Analyzes subjects based on what intervention the subjects actually received – No data should be eliminated • Per-protocol – Analyzes those subjects who precisely followed the protocol – Problematic if compliance is related to prognosis Basic Study Design • Superiority – Trial with the primary objective of showing that the response to the investigational product is superior to a comparator • Equivalence Basic Statistical Concepts – A trial with the primary objective of showing that the response to 2 or more treatments differs by an amount that is clinically unimportant • Noninferiority – Trial with the primary objective of showing that the response to the investigational product is not clinically inferior to a comparative agent 7 Types of Data • Discrete – Nominal – Ordinal • Continuous – Interval – Ratio Types of Data: Ordinal • Responses scored on a continuum, but no consistent level of magnitude between ranks. • Order of numbers is meaningful • Ordinal scale data can be ranked in a specific order, be it low to high or high to low. – Questionnaires: "strongly agree" is scored as 5, "agree" is scored 4, "no opinion" is scored 3, "disagree" is scored 2, and "strongly disagree" is scored 1. Types of Data: Nominal • Most primitive scale and thus the weakest level of measurement • Items (subjects, patients) placed into groups or categories based on some mutual characteristics, which the entire group possesses. • Data is unordered (there is no ranking among the groups) • Examples: – Gender (male, female), outcome (lived or died, cured or not cured, infection or no infection), diagnosis (intracranial hemorrhage or thromboembolism), risk factors (smoking: yes or no), race, etc… Types of Data: Continuous • A predetermined order to the numbering of the scale is present, as is a consistent level of magnitude between each unit of measure. • Examples: heart rate, blood pressure, blood glucose, distance, time, and degrees Kelvin 8 Hypothesis Testing Step 1: Statement of the Null Hypothesis • Tests of a null and research hypothesis set using data obtained from a sample to make inferences about a population parameter • Statistical hypothesis • Process for answering questions • No difference between groups • Denoted by “H0” ¾ Group A – Group B = 0 ¾ Group A = Group B Step 2: Statement of the Research Hypothesis • Alternative hypothesis • Denoted by “H1” • Difference exists between groups ¾ Group A – Group B = 0 ¾ Group A = Group B Hypothesis Testing • Study example – A new weight-loss medication (Drug A) is compared to an existing one (Drug B) to determine if one agent is better at achieving goal BMI at the recommended starting dose • What is the H0? H1? 9 Step 3: Determination of the Significance Level • Alpha (α) • “Goal score” that, when achieved, allows H0 to be rejected and H1 accepted • Decided upon a priori, or before the fact • Generally, established as α < 0.05 Step 4: Evaluation of the Data Alpha (α) • Derived from the raw data and statistical calculations/tables • Statistical significance is generally accepted – Probability of making a type I error is < 0.05 – 1 out of 20 times a type I error is made (5%) • Alpha may be more stringent in some situations – p ≤ 0.01 – 1 out of 100 times a type I error is made (1%) P-Value • P-value • P-value tells us if there is or is not a difference between groups • Result of statistical testing and direct measure of the evidence supporting H0 • P-value does NOT tell anything about the magnitude of difference • Determined a posteriori, or after the fact • Compared directly to alpha (α) to make a decision about study results – Smaller p-values only mean it is less likely “chance” explains the observed differences • If p < α = statistical significance – Statistically significant does not always mean clinically significant 10 Step 5: Decision Regarding the Null Hypothesis • Accept the null hypothesis – No statistically significant difference – “Fail-to-reject” – P-value > alpha • Reject the null hypothesis – Statistically significant difference – “Fail-to-accept” – P-value < alpha Decision Errors • Type I error – α type error (alpha) – Reject H0 when H0 is true (false positive) – To falsely conclude that a significant difference exists between populations/ samples – Due to chance Decision Errors Decision Errors • Type II error – β type error (beta) – Accept H0 when H0 is false (false negative) – To falsely conclude that no significant difference exists between populations/ samples – Due to chance or small sample size “Truth” H0 is true H0 is false Accept H0 No error Type II error Reject H0 Type I error No error Your decision Error type 11 Decision Errors Decision Errors “Truth” Your decision “Truth” H0 is true H0 is false Accept H0 No error Type II error Reject H0 Type I error No error Your decision H0 is true H0 is false Accept H0 No error Type II error Reject H0 Type I error No error Error type “False-positive” result Beta (β) • The probability of making a type II error is defined as beta (β) • Beta (β) – More difficult to derive – Not one single probability value – Often ignored by researchers Error type “False-negative” result Beta (β) • Beta (β) < 0.2 acceptable • Beta (β) < 0.1 ideal • Beta (β) is most commonly used to calculate the number of subjects needed 12 Power • Power is defined by beta (β) – Indicates the probability of the statistical test detecting significant differences when they exist – Analogous to sensitivity • Defined as 1 - β Descriptive Statistics • Used to present, organize, and summarize data • Usually the basic presentation of data • Provide clues as to the appearance of the data – Power of 80% is minimal (1 - 0.2) – Power of ≥ 90% is ideal (1 - 0.1) Measures of Central Tendency • Mean – Arithmetic average of the data – May be computed for continuous data – Extremely sensitive to outliers • Median – – – – The 50th percentile Value above which or below which half of the data points lie Not sensitive to outliers Useful for continuous or ordinal data • Mode – Most commonly obtained value in the distribution – Useful to describe nominal, ordinal, and continuous data Measures of Variability • Percentile – Point on the distribution where a value is larger than x% of the other values in the group • Range – Difference between the largest and the smallest values in the distribution – Highly sensitive to outliers 13 Measures of Variability • Interquartile range – Measure of variability directly related to the median – Range described by the interval between the 25th and 75th percentile values – Clearly defines where the middle 50% of measures occurs and indicates the spread of data – Used to describe the variability for ordinal data Standard Deviation Measures of Variability • Standard deviation (SD) – Describes the variability of data about the sample mean – Meaningful only when it is calculated for normally distributed continuous data – About 68% of the data will fall within ±1 SD and about 95% of data will fall within ±2 SD Inferential Statistics • Used to determine the likelihood that a conclusion, based on the analysis of the data from a sample, is true and represents the population studied 2.5% 2.5% -3SD -2SD -SD X +SD +2SD +3SD • Used to make inferences about the larger population of interest based on the results from the sample 68% 95% 99.7% 14 Inferential Statistics Inferential Statistics • Standard error of the mean (SEM) – Measure of the precision with which a sample mean estimates the population mean – Statistic derived from the SD from a single sample • SEM=SD/√n – Always smaller than SD – Used to calculate confidence intervals Inferential Statistics: Parametric • Methods that use data extrapolated from a sample of the population studies to numerically describe some characteristic of a population • Valid only when the characteristic follows (or nearly follows) the normal distribution in the population studies • Valid only for continuous data • Confidence intervals (CI) – Measurement of the variability of study data – 95% CI is a numerical range that contains the true value for the population 95% of the time – Most commonly used to estimate the true, but unmeasured, population’s mean values for continuous data that are normally distributed Inferential Statistics: Parametric • t-test – Used for independent samples • Paired t-test – Used when 2 groups contain the same people in groups (ie, cross-over study design) • ANOVA (analysis of variance) – Used when comparing 3 or more groups • ANCOVA (analysis of covariance) – Method used for controlling for the effects of multiple confounding variables 15 ANOVA: post-hoc tests • Used to compare the means of the groups two at a time • Less error associated with the use of compared with separate t-tests • Examples Inferential Statistics: Nonparametric • Applied to non-normal distributions or to data that do not meet the criteria for using parametric tests (ie, ordinal and nominal data) – Bonferroni Correction – Scheffè’s method – Tukey’s least significant difference Inferential Statistics: Nonparametric • Mann-Whitney U test – Nonparametric equivalent to the t-test – Used when data are measured on an ordinal scale – Mann-Whitney U test = Wilcoxon Rank Sum • Wilcoxon Signed Rank test – Nonparametric equivalent of the paired t-test – Used for ordinal data Inferential Statistics: Nonparametric • Kruskal-Wallis – Nonparametric equivalent to ANOVA – Used for ordinal data • Friedman – Used for 3 or more groups with dependent samples – Used for ordinal data 16 Inferential Statistics: Nonparametric • Chi Square (X2) – Compares the percentages between 2 or more groups – Most useful for nominal data – Used to answer research questions about rates, proportions, or frequencies – Used with independent samples Inferential Statistics: Nonparametric • Fisher’s Exact test – Used instead of Chi Square if a cell in the matrix has an expected frequency of less than 5 or when you have a very small sample size (eg, 20 to 40) – Samples are independent • McNemar’s Test – Used to compare nominal data from paired samples • Mantel-Haenszel – Used to compare nominal data while controlling for the effects of a confounder Statistical Significance vs Clinical Significance A study comparing the mean INR in the 90 days before and after patients switched from brand name to generic name warfarin was reported in 2099 patients. Results showed that the mean INR before the switch was 2.45 + 0.02 compared to 2.51 + 0.04 after the switch (p<0.0001). Are these results statistically significant? Clinically significant? Format of Outcome Data Yes No Group 1 A B Group 2 C D 17 Relative Risk Relative Risk Reduction • The ratio of risk of an outcome event occurring in the experimental group compared to the risk of the same outcome event occurring in the control group. • Relative risk reduction is a complement to RR • Percent reduction in the experimental group rate compared with the control group event rate • RRR estimates the percentage of baseline risk that is removed as a result of the new therapy • RRR = 1 – RR • If the RRR is zero, there was no effect of the treatment compared with the control • (C/C+D)/(A/A+B) – RR < 1.0 indicates the therapy lessened the risk of developing the adverse outcome – RR = 1.0 denotes no difference between treatments – RR > 1.0 indicated the therapy increased the risk of developing the adverse outcome Absolute Risk Reduction Numbers Needed-to-Treat • This is sometimes called the risk difference • Difference in the event rate between the control group and the experimental group • ARR = (A/A+B) – (C/C+D) • An ARR of zero indicates no difference between comparison groups • Number of patients who require treatment to prevent one additional undesired event • NNT assumes that baseline risk is the same for all patients • Can not be extrapolated beyond study points in time • NNT = 1/ARR • NNT = 1/[A/(A+B) – C/(C+D)] 18 Title A Systematic Approach to Journal Club Presentation Investigators • Do the investigators appear to be qualified to conduct the trial? • Are the investigators affiliated with reputable institutions? • Is a statistician involved with the trial? • Is it descriptive? • Is it accurate? • Does it describe the design, therapy, route of administration, populations, and outcomes assessed? • Does it suggest that one treatment is superior to another? Funding • Is the funding source one that fosters independent study? 19 Journal • Was the trial published in a reputable journal? • Was the study peer reviewed? Abstract • • • • Does it state the hypothesis of the trial? Does it describe how the trial was undertaken? Does it highlight the results accurately? Does it put the essence of the trial into perspective for the reader? • Is it an unstructured, structured, or informational abstract? • Is it free of bias? Introduction • Is it written clearly? • Is it free of bias? • Does it establish the rationale for conducting the trial? • Is it free of current investigation’s results? Objectives • • • • Are the objectives stated? Are the objectives specific? How will the objectives be measured? When and by whom will the objectives be measured? • Are the objectives reasonable or within the scope of the trial? 20 Methods • Study Design – Is the design appropriate for the investigation? • Inclusion Criteria – Are the inclusion criteria explicitly stated? – Are the inclusion criteria appropriate? • Exclusion Criteria – – – – Are the exclusion criteria explicitly stated? Are the exclusion criteria appropriate? Do the exclusion criteria result in a biased sample? Do the exclusion criteria limit the external validity? Methods • Patient selection – Are the subjects healthy volunteers or subjects with the condition that the intervention is meant to improve? – How were the patients selected? – Do the study subjects fairly represent the larger population of interest? – Were the patients randomized? Methods • Study treatment – Single dose vs multiple doses – Fixed doses vs titrating to desired effect – Comparable dosages for different agents – Dosage form, administration schedule, and duration of treatment – Identical placebo – Setting Methods • Study treatment – – – – How was compliance defined and assessed? Were the subjects receiving any other therapy? What was the potential impact of diet? What was the potential impact of changes in lifestyle? 21 Methods • Measurement of drug effects – Are the measurements valid? – Were the measurements standardized? – Were the measurements evaluated by the same person or the same laboratory? – Were the number of measurements identical between groups? – Are the results reproducible? Methods • Data analysis – Intention-to-treat – As-treated – Per-protocol Methods • Terminology – Were important terms defined? • Safety – How were adverse effects monitored? – When were safety assessments conducted? Methods • Statistical analysis – Are the tests appropriate for the type of data? – Are enough data given to do the calculations? – Was power defined? 22 Results • Are the results presented clearly? • Are the results complete? • Are graphs, charts, and illustrations accurate? • Were the results analyzed according to the original objectives? • • • • Discussion • Do the authors explain the limitations of the trial? • Do the authors consider the work of others? • Do the authors draw valid conclusions based on the data obtained? • Do the authors suggest future directions for further research on the topic? References Student Critique Do the authors cite themselves repetitively? Are the hallmark articles included? Are the references up-to-date? Are the references cited representative of the literature available on the topic? • What limitations can be identified in the study? • What strengths can be identified in the study? • Do you agree with the authors’ conclusions? • Will the results of the study impact clinical practice? 23 Useful Resources • Gehlbach SH. Interpreting the medical literature. New York: McGraw-Hill; 2006. • Gaddis ML, Gaddis GM. Introduction to Biostatistics: part 1-6. Annals of Emergency Medicine, 1990 – part 1, basic concepts. Ann Emerg Med. 1990;19:86-9. – part 2, descriptive statistics. Ann Emerg Med. 1990;19:309-15. – part 3, sensitivity, specificity, predictive value, and hypothesis testing. Ann Emerg Med. 1990;19:591-7. – part 4, statistical inference techniques in hypothesis testing. Ann Emerg Med. 1990;19:820-5. – part 5, statistical inference techniques in hypothesis testing with nonparametric testing. Ann Emerg Med. 1990;19:1054-9. – part 6, correlation and regression. Ann Emerg Med. 1990;19:146268. 24