Power analysis and sample size calculation Eirik Skogvoll, MD, PhD
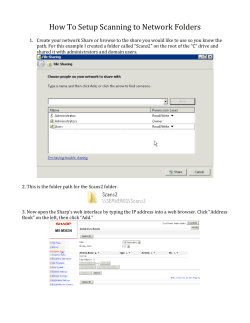
Power analysis and sample size
calculation
Eirik Skogvoll, MD, PhD
Professor, Faculty of Medicine
Consultant, Dept. of Anaesthesiology and Emergency medicine
1
The hypothesis test framework
Rosner tbl. 7.1
P (type II error)
Truth
Conclusion
H0 correct
1– α
α
H0 accepted
H0 rejected
P (type I error)
Power
Type I error: rejecting H0 if H0 is true
Type II error: accepting H0 if H0 is wrong
3
H0 wrong
β
1–β
Hypothesis
A statement about one or more population parameters, e.g.
μ ≤3
μ1 = μ2
σ2 = 14
π = 0,4
π1 =π2
ψ =1
β1 = 0
ρ >0
(Expected value, or “true mean”)
(Two expected values)
(variance)
(probability of a “success”, in a binomial trial)
(two probabilities)
(odds ratio, from a contingency table)
(regression coefficient)
(correlation coefficient)
4
The sample size is a compromise…
• Significance level
• Required or optimal power
• Available resources
– Money
– Time
– Practical issues of recruiting patients or subjects
• The problem under investigation
5
Power
• The probability that some test will detect a difference, if it exists
• With low power, even large differences may go unnoticed:
Absence of evidence is not evidence of absence!
• Power is usually set to 0.8 – 0.9 (80-90 %)
• An infinitely small difference is impossible to detect
• The researcher must specify the smallest difference of (clinical) interest
• Power calculations requires knowledge of the background variability (usually
the standard deviation)
6
Power or significance?
• We wish to reduce the probability of both a type I error (α) and a type II
error (β) , because…
– A small α means that it is diffcult to reject H0
– A small β means that it is easier to reject H0 (and accept H1)
– But minimizing α and β at the same time is complicated, because
α increases as β decreases, and vice versa
• Strategy:
– Keep α at a comfortable level (0.10, 0.05, 0.01);
the maximum ”acceptable” probability of making a type I error; i.e. rejecting H0
when it is true
– Then choose a test that minimizes β, i.e. maximizes power ( =1 - β).
Beware of H1: tests may have different properties!
7
Power (Rosner 7.5)
One- sided alternative hypothesis
H0: μ = μ0
vs.
H1: μ = μ1 < μ0
H0 is rejected if zobs < zα and accepted if zobs ≥ zα .
The decision dose not depend on μ1 as long μ1 < μ0.
(Rosner Fig. 7.5)
Power, Pr (reject H0|H0 wrong) = 1 – Pr(type II error) = 1 – β, however,
depends on μ1.
8
Rosner
Fig. 7.5
H1: μ = μ1 < μ0
9
vs.
H 0: μ = μ 0
⎛ σ2 ⎞
Under H1 , X ~ N ⎜⎜ μ1 , ⎟⎟
n ⎠
⎝
We reject H0 if the observed statistic z is less than critical value zα , i.e. if zobs < zα .
Using the corresponding value for X:
⎛
⎞
⎜ X −μ
⎟
σ ⎞
⎛
0
< zα ⎟ = Pr ⎜ X < μ0 + zα ⋅
Pr ( Z < zα ) = Pr ⎜
⎟
σ
n
⎝
⎠
⎜
⎟
⎜
⎟
n
⎝
⎠
(zα < 0)
10
... remember that Z =
X − μ1
σ
⇔ X =Z⋅
σ
n
+ μ1
n
σ ⎞
σ ⎞
⎛
⎛ σ
+ μ1 < μ 0 + zα
thus, Power = P⎜ X < μ 0 + zα
⎟ = P⎜ Z
⎟
n⎠
n
n⎠
⎝
⎝
11
σ ⎞
σ ⎞
⎛
⎛
zα
zα
⎟
⎜
⎟
⎜
μ
μ
μ
n ⎟ = P⎜ Z < 0 − μ1 +
n⎟
= P⎜ Z + 1 < 0 +
σ
σ
σ ⎟
σ
σ
σ ⎟
⎜
⎜
⎟
⎜
⎟
⎜
n ⎠
n
n
n ⎠
n
n
⎝
⎝
⎞
⎛
⎞
⎛
⎟
⎜
⎟
⎜
−
( μ 0 − μ1 )
μ
μ
μ
μ
−
⎛
⎞
0
1
0
1⎟
⎜
⎟
⎜
= P⎜ Z < zα +
⋅ n⎟
=P Z<
+ zα = P Z < zα +
σ
σ ⎟
⎜
⎟
⎜
σ
⎝
⎠
⎟
⎜
⎟
⎜
n
n
⎠
⎝
⎠
⎝
( μ 0 − μ1 )
⎛
⎞
= Φ⎜ zα +
⋅ n ⎟ ... because P(Z < z ) = Φ ( z ) ... table 3a
σ
⎝
⎠
12
One-sided alternatives, in general:
H0: μ = μ0
vs.
As large as possible …
H1: μ = μ1
| μ0 − μ1 |
| μ0 − μ1 |
⎛
⎞
⎛
⎞
Power = Φ ⎜ zα +
⋅ n ⎟ = Φ ⎜ − z1−α +
⋅ n⎟
σ
σ
⎝
⎠
⎝
⎠
(Rosner, Eq. 7.19)
(remember that zα = – z1-α)
13
Factors influencing power:
•
•
•
•
Power is reduced if α is reduced (zα becomes more negative)
Power increases with increasing |μ0 – μ1|
Power is reduced with increasing σ
Power is increased with increasing n
14
Example (Rosner expl. 7.26)
Birth weight.
H0: μ0 = 120 oz, vs. H1: μ1 = 115 oz,
α = 0.05, σ = 24, n = 100.
Power = Pr(rejecting H0|H0 wrong) =
120 − 115
5 ⋅10
⎞
⎛
= Φ (0.438)
Φ⎜ z0.05 +
⋅ 100 ⎟ = Φ (−1.645 +
24
24
⎠
⎝
= Pr( Z < 0.438) = 0.66
→ Pr(type II error) = Pr(accept H0|H0 wrong) = β= 1– 0.669 = 0,331
15
Example (Rosner expl. 7.29)
Birth weight.
H0: μ0 = 120 oz, vs. H1: μ1 = 110 oz,
α = 0.05, σ = 24, n = 100.
120 − 110
10 ⋅10 ⎞
⎞
⎛
⎛
Φ⎜ z0.05 +
⋅ 100 ⎟ = Φ⎜ − 1.645 +
⎟ = Φ (2.52)
24 ⎠
24
⎝
⎠
⎝
= Pr( Z < 2.52) = 0.99
16
Power for a one sample test, two sided alternative (in general):
H0: μ = μ0
vs.
H1: μ = μ1 ≠ μ0
⎛
⎞
| μ0 − μ1 |
Power ≈ Φ ⎜ − z α +
⋅ n ⎟ (Rosner Eq. 7.21)
σ
⎝ 1− 2
⎠
17
From Power to Sample size…
From Rosner Eq. 7.21 :
⎛
| μ 0 − μ1 | ⋅ n ⎞
⎟ = 1 − β ... now we set (" fix" ) 1 − β
Power = Φ⎜⎜ − z1−α / 2 +
⎟
σ
⎝
⎠
⎛ ⎛
| μ 0 − μ1 | ⋅ n ⎞ ⎞⎟
−1 ⎜
⎟ = Φ −1 (1 − β )
Φ Φ⎜⎜ − z1−α / 2 +
⎟⎟
⎜
σ
⎠⎠
⎝ ⎝
− z1−α / 2 +
| μ 0 − μ1 | ⋅ n
σ
= z1− β ⇔
⇔ μ 0 − μ1 ⋅ n = σ ⋅ (z1− β
| μ 0 − μ1 | ⋅ n
σ
= z1− β + z1−α / 2
σ ⋅ (z1− β + z1−α / 2 )
+ z1−α / 2 ) ⇔ n =
μ 0 − μ1
18
Sample size for one sample test, two sided alternative:
H0: μ = μ0
vs.
H1: μ = μ1 ≠ μ0
σ 2 (z1− β + z1−α / 2 )2
n=
(Rosner Eq. 7.28)
2
(μ0 − μ1 )
19
Two sample test: sample size (Rosner 8.10)
Given X1 ∼ N(μ1, σ21) and X2 ∼ N(μ2, σ22)
H0: μ1 = μ2 vs. H1: μ1 ≠ μ2 (two sided test),
significance level α, and Power 1 – β.
(σ 12 + σ 22 )( z
n=
1−
α
+ z1− β ) 2
2
( μ2 − μ1 )
2
…. in each group (Rosner Eq. 8.26)
20
Rules of thumb
Lehr’s ”quick” equations for two-sample comparison:
• 80 % power, α = 0.05 (two sided), Δ = standardized difference,
m = no. in each group:
m = 16/Δ2
• 90 % power, α = 0.05 (two sided), Δ = standardized difference,
m = no. in each group
m = 21/Δ2
21
The standardized difference
Machin et al. ”Sample size tables for Clinical studies” 3.ed, 2009
Altman 1991 (figure 15.2)
Need to specify the ”standardized difference”:
Δ=
| μ 2 − μ1 |
σ
… the least, clinically important difference expressed as standard
deviations. May vary 0,1 – 1,0, where Δ= 0,1 – 0,2 constitutes a ”small”
difference, while Δ = 0,8 is ”large”.
22
What is the background variability (”noise”)?
•
•
•
From other studies
Pilot data
From the range of possible values (”quick and dirty”):
Range
SD ≈
4
•
This results stems from the basic properties of the Normal (Gaussian) distribution,
in which approx. 95 % of the population are found within ± 2SD of the mean
23
Example
• 80 % power, α = 0.05 (two sided), Δ = standardised difference = 0.5
m = 16/Δ2 = 16/0.25 = 4*16 = 64
Total sample size = 64*2 = 128
24
Nomogram
(Altman 1991)
(total sample size)
Standardised
difference
25
Example
80 % power, α = 0.05
(two sided), Δ = 0.5
N (total) = 125
(total sample size)
Standardised
difference
26
Factors influencing power (1-ß)
•
•
•
•
Power decreases if α is reduced (zα becomes more negative)
Power increases with increasing |μ0 – μ1|
Power decreases with increasing σ
Power increases with increasing sample size ”n”
27
Factors leading to increased sample size (n)
•
•
•
•
Large standard deviation
Strict requirement for α (low level, 0.01- 0.02)
Strict requirement for power (1 – β) (high level: 0.90-0.95)
Low absolute difference between parameters under H1 and H0 (|μ1 – μ0|)
28
Confidence intervals
• Most journals want CI’s reported along with (or instead of) p-values
• The expected length of a confidence interval is determined by the sample
size:
l = 2·tn-1,1-α/2·s/√n
…where
t=
relevant quantile of the t distribution with n-1 degrees of freedom
s = sample standard deviation
n = no. of observations
29
How to make efficient use of your subjects
• Re-use subjects if possible, using a repeated measurements design.
Intra-subject variance will be reduced, as each subject acts as his own
control.
• Enter more than one experimental factor, using a factorial design. Each
subject counts twice (or thrice…) !
• Refine your measurement methods to reduce residual error
• Never, never, never…! dichotomize a continuous outcome variable to a
binary one (i.e. 1 or 0) ! This has the largest variance.
30
Software for sample size calculations
• Machin et al. ”Sample Size Software for Clinical studies” 3.ed, 2009 -- but
you need to set dot (.) as decimal separator /
• Sample Power
• R
• StatExact (for special procedures)
31
References
•
•
•
•
•
•
•
•
Eide, DM. Design av dyreforsøk (kap. 28) i A. Smith: Kompendium i forsøksdyrlære.
http://oslovet.veths.no/dokument.aspx?dokument=262 (2007)
Mead R. The Design of Experiments. Statistical Principles for Practical Applications.
Cambridge: Cambridge Univ. Press; 1990
Altman DG. Practical statistics for medical research. London: Chapman & Hall; 1991.
Altman DG, Bland JM. Absence of evidence is not evidence of absence. BMJ. 1995
Aug 19;311(7003):485.
Rosner B. Fundamentals of Biostatistics. Belmont, CA: Duxbury Thomson
Brooks/Cole; 2005.
Schulz KF, Grimes DA. Sample size calculations in randomised trials: mandatory and
mystical. Lancet. 2005 Apr 9-15;365(9467):1348-53.
Bland JM. The tyranny of power: is there a better way to calculate sample size? BMJ.
2009 October 6, 2009;339(oct06_3):b3985-.
Machin D, Campbell M, Tan SB, Tan SH. Sample Size Tables for Clinical Studies. 3
ed. Oxford: Wiley-Blackwell; 2009.
33
© Copyright 2026