Asymptotic behavior of the sample autocovariance and
Asymptotic behavior of the sample autocovariance and autocorrelation function of the AR(1) process with ARCH(1) errors Milan Borkovec Abstract We study the sample autocovariance and autocorrelation function of the stationary AR(1) process with ARCH(1) errors. In contrast to ARCH and GARCH processes, AR(1) processes with ARCH(1) errors can not be transformed into solutions of linear stochastic recurrence equations. However, we show that they still belong to the class of stationary sequences with regular varying nite-dimensional distributions and therefore the theory of Davis and Mikosch (1998) can be applied. AMS 1991 Subject Classications: primary: 60H25 secondary: 60G10, 60J05 Keywords: ARCH model, autoregressive process, extremal index, geometric ergodicity, heavy tail, multivariate regular variation, point processes, sample autocovariance function, strong mixing School of Operations Research and Engineering, 232 Rhodes Hall, Cornell University, Ithaca, New York 14853, USA, email: [email protected] 1 1 Introduction Over the last two decades, there has been a great deal of interest in modelling real data using time series models which exhibit features such as long range dependence, nonlinearity and heavy tails. Many data sets in econometrics, nance or telecommunications have these common characteristics. In particular, they appear to be reconcilable with the assumption of heavy-tailed marginal distributions. Examples are le lengths, CPU time to complete a job or length of on/o cycles in telecommunications and logreturns of stock indices, share prices or exchange rates in nance. The feature of nonlinearity can be often detected by considering the sample autocorrelation functions (ACFs) of a time series, their absolute values and squares. The reason is the following. A heavy tailed time series that can be represented as an innite moving average process has the property that the sample ACF at lag h converges in probability to a constant (h) although the mathematical correlation typically does not exist (Davis and Resnick (1985),(1986)). However, for many nonlinear heavy tailed sequences the sample ACF at lag h converges in distribution to a nondegenerate random variable. In Resnick and Van den Berg (1998) a test for (non)linearity of a given innite variance time series is proposed, based on subsample stability of the sample ACF. The phenomenon of random limits of sample ACFs was observed rst in the context of innite variance bilinear processes by Davis and Resnick (1996) and Resnick (1997). Davis and Mikosch (1998) studied the weak limit behavior for a large variety of nonlinear processes with regularly varying marginal distributions which satisfy a weak mixing condition and some additional technical assumptions. It is shown in their article that the sample autocovariance function (ACVF) and ACF of such processes with innite 4th but nite second moments have a rate of convergence to the true ACVF and ACF that become slower the closer the marginal distributions are to an innite second moment. In cases of an innite second moment, the limits of the sample ACVF and ACF are nondeterministic. Processes which belong to the framework of Davis and Mikosch (1998) are the ARCH(1) processes, the simple bilinear processes with lighttail noise (Basrak, Davis and Mikosch (1999)) and the GARCH(1,1) processes (Mikosch and Starica (1999)). Finally, Davis, Mikosch and Basrak (1999) embedded the three aforementioned processes to a larger class of processes which still satisfy the conditions for the theory of Davis and Mikosch (1998). These processes have basically the property that they can be transformed to solutions of multivariate linear stochastic recurrence equations. Linear stochastic recurrence 2 equations of this form were considered by Kesten (1973) and Vervaat (1979) and include the important family of the squares of GARCH processes. The aim of this paper is to apply the general theory of Davis and Mikosch (1998) to a dierent type of processes with dierent structure than considered in Davis, Mikosch and Basrak (1999), namely the autoregressive (AR) processes of order 1 with autoregressive conditional heteroscedastic one (ARCH(1)) errors. The class of AR (or more general ARMA) models with ARCH errors were rst proposed by Weiss (1984). In the paper of Weiss, they were found to be successful in modelling thirteen dierent U.S. macroeconomic time series. AR models with ARCH errors are one of the simplest examples of models that can be written by a random recurrence equation of the form Xt = t + t "t ; t 2 N ; (1.1) where "t are iid innovations with mean zero, t is the conditional expectation of Xt (which may or may not depend on t) and the volatility t describes the change of (conditional) variance. Because of the nonconstant conditional variance models of the form (1.1) are often referred to as conditional heteroscedastic models. Empirical work has conrmed that such models t many types of nancial data (log-returns, exchange rate, etc.). In this paper, we concentrate on the AR(1) process with ARCH(1) in order to have a Markov structure and hence make the model analytically tractable. It is dened by specifying t and t as follows: t = Xt 1 and t2 = + Xt2 1 ; (1.2) where 2 R and ; > 0. Note that for = 0 we get just the ARCH(1) model introduced by Engle (1982). The research of the sample ACVF and ACF of the AR(1) process with ARCH(1) errors is motivated by the following. The AR(1) process with ARCH(1) errors is a natural mixture between an AR(1) and an ARCH(1) process. Therefore results of this paper can be seen as a generalization of results for the aforementioned two processes. The weak limit behavior of the ARCH(1) process was studied by Davis and Mikosch (1998). For = 0, the process dened by (1.1) and (1.2) is an AR(1) process. A summary of results about the asymptotical theory of the sample ACFs of AR processes can be found for instance in Brockwell and Davis (1990), Chapter 7.2 and 13.3, or Embrechts, Kluppelberg and Mikosch (1997), Chapter 7.3. AR(1) processes with ARCH(1) errors are not solutions of linear stochastic recurrence equations and there is also no obvious way how to transform them to such equations. However, we 3 show that the processes still belong to stationary weak dependent sequences which are jointly regularly varying. One conclusion of this paper is that AR(1) processes with ARCH(1) errors serve as one of the simplest examples of sequences which do not fulll the framework in Davis, Mikosch and Basrak (1999) but to which the theory of Davis and Mikosch (1998) can still be applied. The paper is organized as follows. In Section2 we introduce the AR(1) model with ARCH(1) errors and consider some basic theoretical properties of it. The weak convergence of the point processes associated with the sequences (Xt ), (jXt j) and (Xt2) is investigated in Section 3. Finally, in Section 4 we present the results concerning the weak convergence of the sample ACVF and ACF of the AR(1) process with ARCH(1) errors, the absolute and squared values. 2 Preliminaries We consider an autoregressive model of order 1 with autoregressive conditional heteroscedastic errors of order 1 (AR(1) model with ARCH(1) errors) which is dened by the stochastic dierence equation q Xt = Xt 1 + + Xt2 1"t ; t 2 N ; (2.1) where ("t ) are i.i.d. random variables, 2 R; ; > 0 and the parameters and satisfy in addition the inequality p E (ln j + "j) < 0 : (2.2) This condition is necessary and sucient for the existence and uniqueness of a stationary distribution. Here " is a generic random variable with the same distribution as "t . In what follows we assume the same conditions for " as in Borkovec and Kluppelberg (1998). These are the so-called general conditions: " is symmetric with continuous Lebesgue density p(x) ; " has full support R ; the second moment of " exists ; and the technical conditions (D:1) (D:3): (D.1) p(x) p(x0) for any 0 x < x0 . 4 (2.3) (D.2) For any c 0 there exists a constant q = q(c) 2 (0; 1) and functions f+(c; ); f (c; ) with f+(c; x); f (c; x) ! 1 as x ! 1 such that for any x > 0 and t > xq p( xp+ c + t2 ) p( px + t 2 ) f+(c; x) ; + t + t x + c t x t ) f (c; x) : p p( p ) p ( + t2 + t2 (D.3) There exists a constant > 0 such that p(x) = o(x p N +1++3q)=(1 q)) ; ( as x ! 1 ; where N := inf fu 0 ; E (j "ju ) > 2g and q is the constant in (D:2). There exists a wide class of distributions which satisfy these assumptions. Examples are the normal distribution, the Laplace distribution or the Students distribution. Conditions (D:1) (D:3) are necessary for determing the tail of the stationary distribution. For further details concerning the conditions and examples we refer to Borkovec and Kluppelberg (1998). Note that the process (Xn)n2N is evidently a homogeneous Markov chain with state space R equipped with the Borel -algebra. The next theorem collects some results on (Xt). Theorem 2.1 Consider the process (Xt ) in (2.1) with ("t ) satisfying the general conditions (2.3) and with parameters and satisfying (2.2). Then the following assertions hold: (a) (Xt) is geometric ergodic. In particular, (Xt) has a unique stationary distribution and satises the strong mixing condition with geometric rate of convergence X (h), h 0. The stationary df is continuous and symmetric. (b) Let F (x) = P (X > x); x 0; be the right tail of the stationary df and the conditions (D:1) (D:3) are in addition fullled. Then F (x) c x ; x ! 1 ; where p p 2 j X j + E + X " ) j X j " ( + p c = 21 p E j + "j ln j + "j (2.4) (2.5) and is given as the unique positive solution to p E (j + "j ) = 1 : (2.6) Furthermore, the unique positive solution is less than 2 if and only if 2 + E ("2) > 1. 5 p Remark 2.2 (a) Note that E (j + "j ) is a function of ; and . It can be shown that for xed , the exponent is decreasing in jj. This means that the distribution of X gets heavier tails when jj increases. In particular, the AR(1) process with ARCH(1) errors has for = 6 0 heavier tails than the ARCH(1) process. (b) The strong mixing property includes automatically that the sequence (Xt ) satises the conditions A(an). The condition A(an ) is a frequently used mixing condition in connection with point process theory and was introduced by Davis and Hsing (1995). See (3.7) for the denition. 2 In order to investigate the limit behavior of the sample ACVF and ACF of (Xt) we dene three auxiliary processes (Yt), (Xet ) and (Zet ) as follows: let (Yt) and (Xet) be the processes given by the random recurrence equations q Yt = Yt 1 + Yt2 1 "t ; t 2 N ; (2.7) and q eXt = jXet + + Xet "tj ; t 2 N ; where the notation is the same as in (2.1), Y = X , Xe = jX j a.s. and set 2 1 0 0 1 0 (2.8) 0 Zet = ln(Xet2) ; t 2 N : It is easy to see that the process (Yt) is not stationary (or at least not non-trivial stationary). However, for Yt Xt large and M 2 N xed, we will see that the sequence Yt ; Yt+1; :::; Yt+M behaves approximately as Xt ; Xt+1; :::; Xt+M (see also Figure 1). This fact will be very important in order to establish joint regular variation of X0; X1 ; :::; XM . Because of the symmetry of ("t), the independence of "t and Xt 1 in (2.1) and the homogeneous Markov structure of (Xt) and (Xet ) it is readily seen that (Xet ) =d (jXtj). Studying the process (Xet) instead of (jXt j) can be often much more convenient. In particular, since (Xet) follows (2.8) the process (Zet ) satises the stochastic dierence equation q eZt = Zet + ln( + e Zet + "t) ; t 2 N ; (2.9) where Ze equals ln(X ) a.s.. Note that (Zet) =d (ln(Xt )). Moreover, (Zet) does not depend on the sign of the parameter since "t is symmetric. The following lemma shows that (Zet ) can be 0 2 1 1 2 2 0 bounded above a high threshold by a random walk with negative drift. The proof of this result 6 60 60 40 40 20 20 0 0 200 0 5 400 600 800 1000 0 200 0 5 400 600 800 1000 0 0 20 20 40 40 60 60 0 10 15 20 25 30 10 15 20 25 30 Figure 1: Simulated sample path of (Xt) with initial value X0 = 50 and parameters = 0:6; = 1; = 0:6 (left) and of (Yt ) with the same initial value and parameters (right) in the case " N (0; 1). Both simulations are based on the same simulated noise sequence ("t). The pictures demonstrate that the processes behave similar for large values. can be found in Borkovec (2000) and is based basically on the recurrence structure of (Zet) in (2.9). The result is crucial for proving Proposition 3.1 . Lemma 2.3 Let a be large enough, Na := inf f 1 j Ze ag and Ze > a. Then 0 Zet Ze0 + Sta for any t Na a.s. ; where Sta is random walk with negative drift given by S0a = 0 and Sta = Sta 1 p + ln ( + e a + "t )2 Moreover, for a " 1, we have Sta a:s: ! St ; 7 (2.10) p 2p e a=2"t 1 + ln 1 : ( + e a + "t )2 f"t<0g p where S0 = 0 and St = St 1 + ln( + "t )2 . 2 3 Weak convergence of some point processes associated with the AR(1) process with ARCH(1) errors In this section we formulate results on the weak convergence of some point processes of the form Nn = n X t=1 Xtm =an ; n = 1; 2; :::; ( (3.1) ) where Xt(m) are random row vectors with dimension m + 1 2 N arbitrary whose components are highly related to the AR(1) process with ARCH(1) errors (Xt) dened in the previous section and (an) is a normalizing sequence of real-valued numbers. The main result in this section is summarized in Theorem 3.3. The proof of this result is basically an application of the theory in Davis and Mikosch (1998). Proposition 3.1 collects some properties of (Xt(m)) which we need for the proof of Theorem 3.3. We follow the notation and the point process theory in Davis and Mikosch (1998) and Kallenberg (1983), respectively. The state space of the point processes considered is Rm+1 nf0g. Write M for the collection of Radon counting measures on Rm+1 nf0g with null measure o. This P n , where n 2 f1; 2; 3; :::g and means that 2 M if and only if is of the form = 1 i i=1 i xi m+1 xi 2 R n f0g distinct and #fi j jxij > y g < 1 for all y > 0 . In what follows we suppose that (Xt) is the stationary AR(1) process with ARCH(1) given by (2.1). ("t) satises the general conditions (2.3) and (D:1) (D:3) and the parameters and are chosen such that (2.2) holds. We start by specifying the random row vectors (X(tm)) and the normalising constants (an) in (3.1) and by introducing some auxilary quantities in order to be in the framework of Davis and Mikosch (1998). For m 2 N0 , dene Xtm = (Xt; Xt ; :::; Xt m) ; t 2 Z; p p p Z m = r ; (r + " ); :::; (r + " ) Qms ( + rs "s ) ( ) ( 0 ) and +1 0 p 0 Ztm = (r + " ) ( ) 0 + 1 1 tY1 0 1 =1 1 p ( + rs "s+1); :::; s=1 8 mY +t 1 s=1 +1 p ! ( + rs "s+1) ; t 2 N ; Q where rs = sign(Ys) is independent of jYs j, (Ys ) is the process in (2.7) and 0i=1 = 1 . Besides, for k 2 N0 arbitrary but xed, dene the stochastic vectors X mk (2k + 1) = (X mk ; X mk ; :::; Xkm ) ( ) ( ) ( ) +1 ( ) and Z m (2k + 1) = (Z m ; Z m ; :::; Z mk ) : ( 0 ( 0 ) ) ( 1 ( 2 ) ) Analogously to Davis and Mikosch (1998) we take j j to be the max-norm in Rm+1, i.e. jxj = j(x ; :::; xm)j = i max jx j : ;:::;m i 0 =0 Now we are able to dene the sequence (an) in (3.1). Let (a(nk;m) ) be a sequence of positive numbers such that P (jX j > a(nk;m) ) (n E (jZ(0m) (2k + 1)j )) 1 ; as n ! 1 : (3.2) For k = 0, we write an = an(0;m) in the following. Note that because of (2.4) one can choose a(nk;m) as a(nk;m) = 2 c E (jZ0(m) (2k + 1)j) = 1 n1= ; n 1 : (3.3) With this notation we can state the following proposition. Proposition 3.1 Let (Xt ) be the stationary AR(1) process with ARCH(1) given by (2.1) and and assume that the conditions of Theorem 2.1 hold. Then (a) (X(tm)) is strongly mixing with a geometric rate of convergence. To be more specic, there exist constants 2 (0; 1) and C > 0 such that for any h m sup A2(X(sm) ; s0);B2(Xs(m) ; sh) jP (A \ B ) P (A) P (B )j =: X m (h) ( ) = X (h m) C h m : (b) X(mk)(2k + 1) is jointly regularly varying with index > 0, more precisely n P (jX(mk)(2k + 1)j > t a(nk;m) ; X(mk) (2k + 1)=jX(mk) (2k + 1)j 2 ) (3.4) !v t E (jZ(0m)(2k + 1)j 1fZ m (2k+1)=jZ m (2k+1)j2 g)=E (jZ(0m)(2k + 1)j) ; t > 0 ; ( 0 ) ( 0 ) v stands for vague convergence. as n ! 1, where the symbol ! 9 (c) Let (pn) be an increasing sequence such that pn ! 0 and nX m (ppn) ! 0 as n ! 1 : ( n ) pn (3.5) Then for any y > 0 1 0 _ jXtm j > an y jX m j > any A = 0 : lim lim sup P @ p!1 n!1 ( ) ( 0 pjtjpn ) (3.6) Remark 3.2 (a) In the spirit of Davis and Mikosch (1998) the jointly regular varying property of X mk (2k + 1) can also be expressed in the more familiar way ( ) n P (jX(mk) (2k + 1)j > t a(nk;m) ; X(mk)(2k + 1)=jX(mk)(2k + 1)j 2 ) !v t P ( ) ; as n ! 1 ; where P ( ) = Pe ((kk) ; :::; k(k) ) 1 , j(k) = Z(km+)j =jZ(0m) (2k + 1)j, j = k; :::; k, and dPe = jZ0(m)(2k + 1)j=E (jZ(0m) (2k + 1)j ) dP : In the following we will basically use this notation. (b) Due to statement (b) in Proposition 3.1 the positive sequence (an) in (3.2) with k = 0 can be also characterized by lim n P (jX(0m)j > an) = 1 : n!1 Hence an can be interpreted as the (approximated) (1 n 1)-quantile of X0(m) . (c) In the case of a strong mixing process, the conditions in (3.5) are sucient to guarantee that (pn) is a A(an )-separating sequence, i.e. E exp n X t=1 ! f (Xtm)=an ) ( E exp pn X t=1 !!kn f (Xtm)=an ) ( ! 0 ; as n ! 1 ; (3.7) where kn = [n=pn] and f is an arbitrary bounded non-negative step function on Rm n f0g . Note that (pn) is in the case of a strong mixing process independent of (an). Proof. (a) This is an immediate consequence of the strong mixing property of (Xn) and the fact that strong mixing is a property of the underlying -eld. (b) Fix t > 0 and let > 0 be small enough such that t 2 > 0. Moreover, choose B 2 B(S (2k+1)(m+1) 1) arbitrary, where S := S (2k+1)(m+1) 1 denotes the unit sphere in R(2k+1)(m+1) with respect to the max-norm j j. Dene B = fx 2 S j 9 y 2 B : jx yj 2=(t 2)g and B = fx 2 B j jx yj 2=(t 2) 8y 2 S n B g. Note that B B B . Next set Yt(m) := (Yt ; Yt+1; :::; Yt+m) ; t 2 N0 ; and Y0(m)(2k +1) = (Y0(m); Y1(m); :::; Y2(mk )), where 10 (Yt ) is the process given in (2.7). Using the denition of the process (Yt) and of the stochastic vectors Z(tm), it can be readily seen that Y m (2k + 1) = jX j Z m (2k + 1) : ( 0 ) (3.8) ( ) 0 0 The basic idea of proving (3.4) is now to approximate X(mk) (2k + 1) by Y0(m)(2k + 1). Because of the stationarity of (Xt) it is sucient to compare X(0m)(2k + 1) with Y0(m) (2k + 1). First we bound the probability in the left hand side of (3.4) from above as follows. n P jX(mk)(2k + 1)j > t a(nk;m) ; X(mk) (2k + 1)=jX(mk) (2k + 1)j 2 B = n P jX(0m) (2k + 1)j > t a(nk;m) ; X0(m)(2k + 1)=jX(0m)(2k + 1)j 2 B n P jX(0m) (2k + 1) Y0(m) (2k + 1)j > a(nk;m) + n P jX(0m) (2k + 1)j > t a(nk;m) ; X(0m) (2k + 1)=jX(0m) (2k + 1)j 2 B ; jX0(m) (2k + 1) Y0(m)(2k + 1)j a(nk;m) n P jX(0m) (2k + 1) Y0(m) (2k + 1)j > a(nk;m) + n P jY0(m)(2k + 1)j > (t ) a(nk;m) ; Y0(m) (2k + 1)=jY0(m) (2k + 1) 2 B ; jY0(m)(2k + 1) Y0(m)(2k + 1)j a(nk;m) =: (I1) + (I2) ; where the last inequality follows from the fact that for any x; y 2 R(2k+1)(m+1) the inequalities jx yj a(nk;m) and jxj > ta(nk;m) imply jyj > (t )a(nk;m) , jx=jxj y=jxjj =t and jjyj=jxj 1j =(t 2). The rest is a triangular argument. First, we consider (I1). By the denition of the max-norm and due to the Boolean and Markov inequalities, we derive (I1) = n P (0smax jX Ysj > a(nk;m) ) 2k+m s q = n P (0smax j + Xs 2k+m 2 q 1 p Xs2 1j j"s j > a(nk;m) ) n P ( smax j" j > ank;m = ) k m s E (j"j ) ; (2k + m + 1) nk;m p (a = ) ( 0 ) 2 + + ( n E (j"j+ ) ) + where > 0 is chosen such that < 1 . This is possible because of the assumption (D:3). Using (3.3) the right hand side converges to zero. 11 Now we estimate (I2). By (3.8) , we have (I2) n P jX0j jZ(0m) (2k + 1)j > (t )a(nk;m) ; Z(0m)(2k + 1)=jZ(0m)(2k + 1)j 2 B = n P jX0j jZ(0m) (2k + 1)j 1fZ m (2k+1)=jZ m (2k+1)j2B g > (t )a(nk;m) ( 0 ) ( 0 ) Note that jX0 j and Z(0m) (2k + 1) are independent, nonnegative random variables. Moreover, jX0j is regularly varying with index > 0 and E (jZ(0m) (2k + 1)j) < 1. Thus, a result of Breiman (1965) yields that (I2) behaves asymptotically as n P jX0j > (t )a(nk;m) ) E (jZ(0m)(2k + 1)j 1fZ m (2k+1)=jZ m (2k+1)j2B g E (jZ(0m)(2k + 1)j 1fZ m (2k+1)=jZ m (2k+1)j2B ) (t ) ; as n ! 1 ; E (jZ(0m)(2k + 1)j) where we used in the second line (3.2). Because > 0 is arbitrary and B # B as # 0 we have found that ( 0 ( 0 ) ( 0 ) ( 0 ) ) lim sup n P jX(mk) (2k + 1)j > t a(nk;m) ; X(mk)(2k + 1)=jX(mk)(2k + 1)j 2 n!1 t E jZ m (2k + 1)j 1fZ m ( 0 ) ( 0 ) jZ m (2k + 1)j) : m) (2k+1)j2 g )=E ( (2k+1)=jZ ( 0 ( ) 0 (3.9) Next we proceed to establish that the inequality (3.9) also holds in the converse direction for lim inf. With similar arguments as above, we have n P jX(mk)(2k + 1)j > t a(nk;m) ; X(mk) (2k + 1)=jX(mk) (2k + 1)j 2 B n P jY0(m)(2k + 1)j > (t + ) a(nk;m) ; Y0(m)(2k + 1)=jY0(m)(2k + 1) 2 B ; jX(0m) (2k + 1) Y0(m)(2k + 1)j a(nk;m) n P jY0(m)(2k + 1)j > (t + ) a(nk;m) ; Y0(m)(2k + 1)=jY0(m)(2k + 1) 2 B n P jX(0m) (2k + 1) Y0(m) (2k + 1)j > a(nk;m) E (jZ(0m)(2k + 1)j 1fZ m (2k+1)=jZ m (2k+1)j2B g) (t + ) ; as n ! 1 : E (jZ(0m)(2k + 1)j) Since again > 0 is arbitrary the statement follows. (c) We start by rewriting the probability in statement (c). ( 0 P _ ( 0 ) jXtm (2k + 1)j > an y jX m (2k + 1)j > an y ( pjtjpn ) ) ( ) 0 = P p tmax jXtj > any 0max jX j > an y j 2k+1 j n p+2k+1 + P ptmax j X j > a y max j X j > a y t n j n p +2k+1 0j 2k+1 =: (J1) + (J2) : n 12 In what follows we consider only (J1). (J2) can be treated in a similar way. First note that (J1) k P (max X 2 +1 j =0 2k+1 X P j =0 P (jXj j > an y) pnt p+2k+1 jXt j > an y; jXj j > any) P (jXj j > any) P (max0j 2k+1 jXj j > any) max jX j > any jX0j > any pn j t p+2k+1 j t 2(k + 1) P 2(k + 1) jXt j > an y jX j > any max 0 pn (2k+1)t p+2k+1 pX +2k+1 P jXt j > an y jX0j > any : pn (2k+1) t= Moreover, using again the property of conditional probability together with the stationarity of (Xt ) and substituting t by t, we get that (J1) is bounded by 2(k + 1) t= pn = 2(k + 1) P jX tj > any jX0 j > an y (2k+1) pn+(2 Xk+1) t=p pX +2k+1 k P jXt j > any jX0j > an y : (2 +1) Recalling that (Zet ) = (ln(Xet)2) =d (ln(Xt )2) it follows that the last expression can be also expressed by 2(k + 1) pn+(2 Xk+1) t=p k P Zet > ln(any)2 Ze0 > ln(any)2 : (2 +1) Next, set Na = inf fs 2 N ; Zes a g as in Lemma 2.3. Choose the threshold a large enough =4 p p for a xed in order to guarantee that E ( + e a + ")2 2 e a=2"1f"<0g p u 2 (0; 1). This is possible because of (2.2) which implies that E (j + "j ) < 1 for all u 2 (0; ) and the fact that p p E ( + e a + ")2 2 e a=2"1 f"<0g = 4 p ! E j + "j= ; a ! 1 ; 2 by the dominated convergence theorem. We derive k p X (J1) 2(k + 1) + 2( +1) pnX +2k =p k =1 1 pn+(2 Xk+1) t=p (2k+1) pn+(2 Xk+1) t p (2 +1) = k P (Zet > ln(any)2; Na = j Ze0 > ln(any)2) P (Zet > ln(any)2; Na = j ln Ze0 > ln(any)2) (2 +1) 13 + 1 X pn+(2 Xk+1) =pn+(2k+1) t=p k P (Zet > ln(any)2; Na = j Ze0 > ln(any)2) (2 +1) =: 2(k + 1) (K1 ) + (K2) + (K3) It can be shown now (see Borkovec (2000)) that the summands (K1), (K2) and (K3 ) tend to zero as n ! 1 and then p ! 1. The basic idea underlying this result is to use Lemma 2.3 and the fact that the expression n P (Zet > ln(any)2 j Ze0 = x) is uniformly bounded for any n 2 N; x 2 [e n; ea ] and t 2 N . This nishes the proof. 2 Proposition 3.1 provides some properties for (Xt(m)) and (Xt(m) (2k + 1)) which are just the required assumptions in Davis and Mikosch (1998) for weak convergence of point processes of the form (3.1). If we dene f = f 2 M j (fx j jxj > 1g) = 0 and (fx j x 2 S mg) > 0g) M f) be the Borel -eld of M f then the following theorem is an immediate and if we let B(M consequence of Proposition 3.1. Theorem 3.3 Assume (Xt) is the stationary AR(1) process with ARCH(1) errors satisfying the conditions of Theorem 2.1. Then 1 X 1 n X X X X Nn = Xt=an ! N = Pi Qij ; t=1 where Xt = X(tm) , (3.10) i=1 j =1 P1 is a Poisson process on (0; 1] with intensity i Pi Yk p =1 (dy) = E (sup ( + "s ) P 1) y k1 s=1 1 dy P and P is a Pareto()-distributed random variable, independent of ("s). The process 1 i=1 Pi is P independent of the sequence of iid point processes 1 j =1 Qij , i 1, with joint distribution Q on f; B(M f)), where Q is the weak limit of (M Ee j0(k) j _k j =1 jjk j 1f g ( ) + X jtjk tk ( ) e k _k k =E j j jj j ( ) 0 ( ) j =1 + (3.11) as k ! 1, and the limit exists. Ee is the expectation with respect to the probability measure dPe dened in Remark 3.2(a). 14 Remark 3.4 Analogous results can be found for the vectors jXtj = jXtm j = (jXtj; :::; jXt mj) and Xt = Xtm = (Xt ; :::; Xt m) ; t 2 Z; m 2 N ; ( ) )2 ( 2 + 2 2 + by using (3.10) and the continuous mapping theorem. Thus, under the same assumptions as in Theorem 3.3, we have NnjXj = and n X t=1 jXt j=an ! 1 X 1 X i=1 j =1 PijQij j XX X PiQij NnX = Xt =an ! 1 1 n 2 2 t=1 i=1 j =1 2 where the sequences (Pi), (Qij ) are the same as above and jQij jl = (jQij jl ; jQij jl ; :::; jQijm jl ) ; l = 1; 2 : (0) (1) ( ) Proof. The proof is simply an application of Theorem 2.8 in Davis and Mikosch (1998). The assumptions of this theorem are satised because of Proposition 3.1. Finally, the extremal index W = limk!1 E j0(k) j kj=1 jj(k) j + =E j0(k) j of the AR(1) process with ARCH(1) errors is not zero and is specied by the formula (see Borkovec (2000)) Yk p = E (sup ( + "i ) P 1) ; k1 i=1 where P is a Pareto()-distributed random variable, independent of ("s). Hence the statement follows. 2 4 Asymptotic behavior of the sample ACVF and ACF In what follows we derive the limit behaviour of the sample ACVF and ACF of the stationary AR(1) process with ARCH(1) considered in the previous sections. The point process results of the section 3 will be crucial. Dene the sample ACVF of (Xt ) by nXh n;X (h) = n1 Xt Xt+h ; h = 0; 1; ::: ; t=1 15 and the corresponding sample ACF by n;X (h) = n;X (h)=n;X (0) ; h = 0; 1; ::: : The sample ACVF and ACF for (jXt j) and (Xt2) are given in the same way. Moreover, we write X (h) = E (X0Xh ) ; jX jl (h) = E (jX0jl jXh jl ) ; and X (h) = X (h)=X (0) ; jX jl (h) = jX jl (h)=jX jl (0) ; l = 1; 2 h = 0; 1; ::: if these quantities exist. If this is the case straightforward calculations yield X (h) = h X (0) = h =(1 2 E ("2 )) and X (h) = ( + E (" 2 2 2 ))h X 2 (0) + E (" 2 )X (0) h X 1 j =0 (2 + E ("2 ))j ; h 0 ; where X (0) = 2X (0)(22E ("2) + E ("4 ))=(1 4 62 E ("2 ) 2 E ("4)) : 2 Mean-corrected versions for the sample ACVF and ACF can also be investigated. However one can show (with the same approach as in the proof of Theorem 4.1) that the limits stay the same (see also Remark 3.6 of Davis and Mikosch (1998)). In order to state our results we have to introduce several mappings. Let > 0, xt = m+1 (m) (x(0) n f0g and dene the mappings t ; :::; xt ) 2 R Th;k; : M ! R by P P n = 1 n1 T 1; 1; 1 ; P1 t=1 t xt P1 t=1 (th)fjx(kt) j>g Th;k; t=1 nt xt = t=1 nt xt xt 1fjxt j>g ; h; k 0 ; (0) (0) where nt 2 N0 for any t 1. Since the set fx 2 Rm+1 n f0g j jx(h) j > g is bounded for any h = 0; :::; m the mappings are a.s. continuous with respect to the limit point processes N X, N jXj and N X . Consequently, by the continuous mapping theorem, we have in particular 2 XX X 1fjPiQij j>g T 1; 1; (NnX) = 1fjXt j>g !d T 1; 1; (N X) = 1 1 n t=1 (0) i=1 j =1 16 (0) (4.1) and for any h; k 0 X X 2 (h) (k) X Pi Qij Qij 1fjPi Qij j>g : (4.2) Th;k; (NnX) = Xt(h) Xt(k) 1fjXt j>g !d Th;k; (N X) = 1 1 n (0) t=1 i=1 j =1 (0) Note that, with obvious modications, (4.1) and (4.2) hold also for NnjXj and N jXj respectively NnX and N X . The following theorem collects the weak limit results of the sample ACVF and ACF of (Xt), (jXt j) and (Xt ) depending on the tail index > 0. The weak limits turn to be innite variance stable random vectors. However, they are only functionals of point processes and have no explicit representation. Therefore, the results are only of qualitative nature and explicit asymptotic condence bounds for the sample ACVFs and ACFs can't be constructed. 2 2 Theorem 4.1 Assume (Xt) is the stationary AR(1) process with ARCH(1) errors satsifying the conditions of Theorem 2.1 with E ("2) = 1. Let > 0 be the tail index in (2.6) and (an) be the sequence satisfying (3:3) for k = 0. Then the following statements hold: (1) (a) If 2 (0; 2), then nan 2n;X (h) h=0;:::;m !d (VhX )h=0;:::;m ; d (V X =V X ) (n;X (h))h=1;:::;m ! h 0 h=1;:::;m ; and nan 2n;jX j (h) h=0;:::;m !d (VhjX j )h=0;:::;m ; n;jX j (h) h=1;:::;m !d (VhjX j =V0jX j )h=1;:::;m ; where the vectors (V0X ; :::; VmX ) and (V0jX j ; :::; VmjX j ) are jointly =2-stable in Rm+1 with point process representation VhX and VhjX j = 1 X 1 X i=1 j =1 = 1 X 1 X i=1 j =1 (h) Pi2 Q(0) ij Qij (h) Pi2jQ(0) ij jjQij j ; h = 0; :::; m ; respectively . (b) If 2 (0; 4), then nan 4n;X (h) h=0;:::;m !d (VhX )h=0;:::;m ; n;X (h) h=1;:::;m !d (VhX =V0X )h=1;:::;m ; 2 2 2 2 17 2 where (V0X ; :::; VmX ) is jointly =4-stable in Rm+1 with point process representation 2 2 VhX 2 = 1 X 1 X i=1 j =1 (h) 2 Pi4 (Q(0) ij Qij ) ; h = 0; :::; m : respectively, (2) (a) If 2 (2; 4) and E ("4) < 1, then nan 2(n;X (h) X (h)) h=0;:::;m !d (VhX )h=0;:::;m ; nan 2(n;X (h) X (h)) h=1;:::;m !d X1(0)(VhX X (h)V0X )h=1;:::;m and nan 2(n;jX j (h) jX j (h)) h=0;:::;m !d (VhjX j )h=0;:::;m ; nan 2(n;jX j (h) jX j (h)) h=1;:::;m !d jX1j (0)(VhjX j jX j (h)V0jX j )h=1;:::;m ; where the vectors (V0X ; :::; VmX ) and (V0jX j ; :::; VmjX j ) are jointly =2-stable in Rm+1 with ; V X = Ve X + V X ; m 1 ; m m m V0X = Ve0X 1 (2 + ) 1 1 and p V0jX j = V0X ; VmjX j = VemjX j + E (j + "j)VmjX j1 ; m 1 : Furthermore, (Ve0X ; :::; VemX ) and (Ve0jX j ; :::; VemjX j ) are the distributional limits of T1;1; (N X) (2 + )T0;0; (N X); T0;h; (N X) T0;h and T1;1; (N jXj) X 1; (N ) h=1;:::;m nan 4(n;X 2 nan 4 (n;X (h) X (h)) h=0;:::;m !d (VhX )h=0;:::;m ; d 1 (0)(V X (h)V X ) (h) X (h)) h=1;:::;m ! X h=1;:::;m ; 0 h X 2 2 2 2 2 2 2 where (V0X ; :::; VmX ) is jointly =4-stable in Rm+1 with 2 2 ; V X = Ve X + ( + )V X ; m 1 ; m m m V0X = Ve0X 1 (4 + 62 + 2 E ("4)) 2 p ( + )T0;0; (N jXj); T0;h; (N jXj) E (j + "j)T0;h 1; (N jXj) h=1;:::;m ; 2 respectively, as ! 0. (b) If 2 (4; 8) and E ("8 ) < 1, then 2 2 1 18 2 2 2 1 and (Ve0X ; :::; VemX ) is the distributional limit of 2 2 T1;1; (N X ) (4 + 62 + 2 E ("4))T0;0; (N X ); T0;h; (N X ) (2 + )T0;h 2 2 as ! 0. (3) (a) If 2 (4; 1), then n1=2(n;X (h) X (h)) n1=2(n;X (h) X (h)) and 2 d (GX ) ! h h ;:::;m h=0 d 1 ! X (0)(GXh h=1;:::;m =0 X) ; 1; (N h=1;:::;m 2 ;:::;m ; X (h)GX0 )h=1;:::;m n1=2(n;jX j(h) jX j (h)) h=0;:::;m !d (GjhX j)h=0;:::;m ; 1=2 n (n;X (h) X (h)) h=1;:::;m !d X1 (0)(GjhX j X (h)Gj0X j)h=1;:::;m ; where the limits are multivariate Gaussian with mean zero. (b) If 2 (8; 1), then = n (n;X (h) X (h)) h = 1 2 2 2 n1 2(n;X (h) X (h)) 2 2 d (GX ! h )h ;:::;m ; ;:::;m !d X (0)(GXh X (h)GX )h ;:::;m 2 =0 =0 h=1 1 2 2 2 2 0 =1 ;:::;m ; where the limits are multivariate Gaussian with mean zero. Remark 4.2 (a) Theorem 4.1 is a generalization of results for the ARCH(1) process (see Davis and Mikosch (1998)). They use a dierent approach which does not extend to the general case because of the autoregressive part of (Xt ). (b) The assumption 2 := E ("2) = 1 in the theorem is not a restriction. In cases where the second moment is dierent from one consider the process (Xbt) dened by the stochastic recurrence equation q Xbt = Xbt 1 + =2 + Xbt2 1 "t = ; t 2 N ; where the notation is the same as for the process (Xt) in (2.1). Note that (Xbt) = (Xt=2 ). Since the assumptions in the theorem do not dependent on the parameter the results hold for (Xbt) and hence they also hold for (Xt ) replacing the limits (VhX ; VhjX j ;VhX )h=0;:::;m by 4 (VhX ; VhjX j ;VhX )h=0;:::;m and (GXh ; GjhX j;GXh )h=0;:::;m by 4 (GXh ; GjhX j;GXh )h=0;:::;m, respectively. 2 2 2 19 2 (c) Note that the description of the distributional limits in part (2) of Theorem 4.1 is dierent than in Theorem 3.5 of Davis and Mikosch (1998). In the latter theorem the condition lim lim sup var an #0 n!1 2 nXh t=1 ! Xt Xt+h 1fjXtXt hjang = 0 + 2 is required. However, this condition is very strong and does not seem to be in general fullled when (Xt ) is correlated (see e.g. Theorem 1.1 of Rio (1993) for a possible justication) . Therefore, we choose another way and establish the convergence in distribution of the sample ACVF directly from the point process convergence in Theorem 3.3. Proof. Statements (1a) and (1b) are immediate consequences of Theorem 3.5(1) of Davis and Mikosch (1998). Note that all conditions in this theorem are fullled because of Proposition 3.1 and Theorem 3.3. Statements (3a) and (3b) for the sample ACVFs follows from standard limit theorems for strongly mixing sequences (see e.g. Theorem 3.2.1 of Zhengyan and Chuanrong (1996)). The limit behavior for the ACFs can be shown in the same way as e.g. in Davis and Mikosch (1998), p.2062 . It remains to show (2a) and (2b). We restrict ourselves to the case (jXtj) and only establish joint convergence of (n;jX j(0); n;jX j (1)). All other cases can be treated similar or even easier. Recall that (Xet ) =d (jXt j), where the process (Xet) is dened in (2.8). Thus it is sucient to study the sample ACVF of the process (Xet). We start by rewriting n;Xe (0) using the recurrence structure of (Xet ) nan n;Xe (0) Xe (0) = an 2 = (2 + )an 2 n X e 2 n X e t=1 Xt2+1 E (Xe 2) Xt2 E (Xe 2) t q n X e 2Xt + Xet "t + ( + Xet )("t + an =1 2 2 t=1 We conclude that for any > 0 , n X 1 (2 + ) nan 2 n;Xe (0) Xe (0) = an 2 t=1 +1 ( + Xet2 )("2t+1 1)1fXetang + 2an 2 q n X e t=1 Xt + Xet2 "t+11fXetang 20 2 2 +1 1) : + an 2 n q X e Xt + Xet "t + ( + Xet )("t t=1 2 2 +1 2 +1 1) 1fXet>ang + oP (1) =: (I1) + (I2) + (I3) + oP (1) : We show rst that (I1) and (I2) converge in probability to zero. Note that the summands in (I1) are uncorrolated. Therefore, var(I1) = an 4 an 4 n X t=1 var ( + Xet2 ) 1fjXetjang ("2t+1 1) n X t=1 E ( + Xet2 )2 1fjXetjang E ("2t+1 1)2 const ; as n ! 1 ; ! 0 ; as # 0 ; 4 where the asymptotic equivalence comes from Karamatas theorem on regular variation and the tail behavior of the stationary distribution of (Xet). Note that the condition E ("4 ) < 1 is crucial. Analogously, one can show that lim lim var(I2) = 0 : #0 n!1 Now we consider (I3). (2.8) yields (I3) = an 2 n X e t=1 Xt2+11fXet>ang (2 + )an 2 n X e t=1 Xt21fXet>ang an 2 =d T1;1; (NnjXj) (2 + )T0;0; (NnjXj) an 2 T 1; 1; (NnjXj) !d T1;1; (N jXj) (2 + )T0;0; (N jXj) ; n X t=1 1fXet>ang (4.3) where the limit has expectation zero. Finally, following the same arguments as in Davis and Hsing (1995), pp. 897-898, the right hand side in (4.3) converges in distribution to a =2-stable random variable, as ! 0 . Now consider n;Xe (1). We proceed as above and write nan 2 n;Xe (1) Xe (1) = an 2 = an 2 n 1 X t=1 n X Xet Xet 1 t=1 +1 E (Xe0Xe1) f"t (Xet) E (f"t (Xet)) + an 2 +1 +1 =: (J1) + (J2) ; 21 n X e 1 t=1 p p Xt2j + "t+1j E (Xe 2)E (j + "j) p p where fz (y) = jyj jy + + y2 z j jy + yz j for any y; z 2 R. First, we show that (J1) converges in probability to zero. Observe for that purpose that var jan 2 n X 1 t=1 var an = an 4 f"t (Xet ) E (f"t (Xet))j +1 2 n X t=1 n X n X p t=1 s=1 ! +1 jf"t (Xet )j ! (4.4) +1 cov(jf"t (Xet )j; jf"s (Xes )j) : +1 +1 Now note that jfz (y)j jyj jz j for any y; z 2 R. Therefore and since > 2 there exists a > 0 such that p E (jf"(Xe )j2+) E (j"j2+)E (jXe j2+) < 1 : (4.5) Because of (4.5) and the geometric strong mixing property of (Xet) all assumptions of Lemma 1.2.5 of Zhengyan and Chuanrong (1996) are satised and we can bound (4.4) by const an 4 n n X s=1 (2=(2+))s (4.6) which converges to zero as n ! 1 since < 4. Next we rewrite (J2) and get p (J2) = E (j + "j)nan 2 n;Xe (0) Xe (0) + an 2 + an 2 n X e 1 t=1 nX1 t=1 p p p p Xt2 1fXetang j + "t+1 j E (j + "j) Xet2 1fXet>ang j + "t+1 j E (j + "j) = (K1) + (K2) + (K3) : d T (N jXj) (2 + )T (N jXj). Moreover, using the same arguments as By (4.3), (K1) ! 1;1; 0;0; before one can show that lim#0 limn!1 var(K2) = 0. Hence (K2 ) = oP (1). It remains to consider (K3). We begin with the decomposition (K3) = an 2 n X e 1 t=1 q p Xt 1fXet>ang jXet + Xet "t+1j jXet + + Xet2"t+1 j n n X X p e e + an Xt Xt 1fXet>ang an Xet 1fXet>angE (j + "j) : 1 2 t=1 1 2 +1 2 t=1 Proceeding the same way as in (4.4)-(4.6) the rst term converges in probability to zero. Thus, p (K3) =d oP (1) + T0;1; (NnjXj) E (j + "j)T0;0; (NnjXj) p !d T ; ; (N jXj) E (j + "j)T ; ; (N jXj) ; 00 01 22 where the limit has zero mean and converges again to a =2-stable random variable as # 0. Since for the distributional convergence only the point process convergence and the continuous mapping theorem has been used, it is immediate that the same kind of argument yields the joint convergence of the sample autocovariances to a =2-stable limit as described in the statement. Finally, the asymptotic behavior of the sample ACF can be shown in the same way as in Davis and Mikosch (1998), p.2062 . 2 Acknowledgement I am very grateful to Thomas Mikosch for useful comments and advice. Furthermore, I thank Claudia Kluppelberg for making me aware to this problem. References [1] Basrak, B., Davis, R.A. and Mikosch, T. (1999) The sample ACF of a simple bilinear process. Stoch. Proc. Appl. 83, 1{14. [2] Bingham, N.H., Goldie, C.M. and Teugels, J.L. (1987) Regular Variation. Cambridge University Press, Cambridge. [3] Borkovec, M. and Kluppelberg, C. (1998) The tail of the stationary distribution of an autoregressive process with ARCH(1) errors. Preprint. [4] Borkovec, M. (2000) Extremal behavior of the autoregressive process with ARCH(1) errors. Stoch. Proc. Appl. 85/2, 189-207. [5] Breiman, L. (1965) On some limit theorems similar to the arc-sin law. Theory Probab. Appl. 323{331. 10, [6] Brockwell, P.J. and Davis, R.A. (1990) Time Series: theory and Methods. Springer, New York. [7] Davis, R.A. and Hsing, T. (1995) Point process and partial sum convergence for weakly dependent random variables with innite variance. Ann. Probab. 23, 879{917. [8] Davis, R.A. and Mikosch, T. (1998) The sample autocorrelations of heavy-tailed processes with application to ARCH. Ann. Statist. 26, 2049{2080. [9] Davis, R.A. Mikosch, T., and Basrak, B. (1998) The sample ACF of solutions to multivariate stochastic recurrence equations. Technical Report. 23 [10] Davis, R.A. and Resnick, S.I. (1985) More limit theory for the sample correlation function of moving averages. Stoch. Proc. Appl. 20, 257{279. [11] Davis, R.A. and Resnick, S.I. (1986) Limit theory for the sample covariance and correlation functions of moving averages. Ann. Statist. 14, 533{558. [12] Davis, R.A. and Resnick, S.I. (1996) Limit theory for bilinear processes with heavy tailed noise. Ann. Appl. Probab. 6, 1191{1210. [13] Embrechts, P., Kluppelberg, C. and Mikosch, T. (1997) Modelling Extremal Events for Insurance and Finance. Springer, Heidelberg. [14] Engle, R. F. (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of U.K. ination. Econometrica 50, 987{1007. [15] Kallenberg, O. (1983) Random Measures, 3rd edition. Akademie-Verlag, Berlin. [16] Kesten, H. (1973) Random dierence equations and renewal theory for products of random matrices. Acta Math. 131, 207{248. [17] Mikosch, T. and Starica, C. (1998) Limit theory for the sample autocorrelations and extremes of a GARCH(1,1) process. Technical report. [18] Resnick, S.I. (1997) Heavy tail modeling and teletrac data. With discussion and a rejoinder by the author. Ann. Stat. 25, 1805{1869. [19] Resnick, S.I. and Van den Berg, E. (1998) A test for nonlinearity of time series with innite variance. Technical report. [20] Rio, E. (1993) Covariance inequalities for strongly mixing processes. Ann. Inst. Henri Poincare 29, 587{597. [21] Vervaat, W. (1979) On a stochastic dierence equation and a representation of nonnegative innitely divisible random variables. Adv. Appl. Prob. 11, 750{783. [22] Weiss, A.A. (1984) ARMA models with ARCH errors. J. T. S. A. 3, 129{143. [23] Zhengyan, L. and Chuanrong, L. (1996) Limit Theory for Mixing Dependent Random Variables, Kluwer Academic Publishers, Dordrecht. 24 1.0 -0.5 0.0 0.5 1.0 0.5 0.0 -0.5 5 10 15 20 0 5 10 15 20 0 5 10 15 20 -0.5 0.0 0.5 1.0 0 Figure 2: ACFs of the AR(1) process with ARCH(1) errors with standard normal distributed innovations ("t ) and parameters = 0:2; = 1 and = 0:4 (top, left), = 0:4, = 1 and = 0:6 (top, right) and = 0:8, = 1, = 0:6 (bottom). In the rst case = 5:49, in the second = 2:87 and in the last = 1:35. The dotted lines indicate the 5% and 95%-quantiles of the empirical distributions of the sample ACFs at dierent lags. The underlying simulated sample paths have length 1000. The condence bands were derived from 1000 independent simulations of the sample ACFs at these lags. The plots conrm the dierent limit behavior of the sample ACFs as described in this article. 25
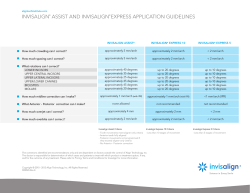
© Copyright 2026