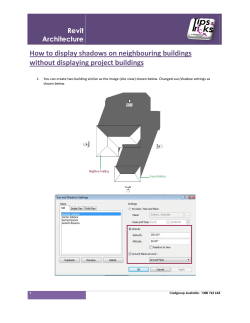
EGGN 512
Computer Vision
Sample Problem Set - SOLUTIONS
The exam will be closed book, but handwritten notes are allowed. The problems below are
representative of exam problems (although there may be more problems than would appear on
the actual exam). Some of the problems below are drawn from previous exams.
For reference, here are some equations (these will be provided on the exam):

A
B
The rotation matrix for XYZ fixed angles is:
RXYZ  X , Y ,  Z   RZ ( Z ) RY (Y ) RX ( X )
0 
 cz  sz 0   cy 0 sy   1 0




  sz cz 0   0 1 0   0 cx  sx 
0
0 1    sy 0 cy   0 sx cx 

where
cx  cos( X ), sy  sin(Y ), etc

The matrix for a rotation about the axis k by an angle  is
 k x k x v  c k x k y v  k z s k x k z v  k y s 


Rk     k x k y v  k z s k y k y v  c k y k z v  k x s 
 k k v  k s k k v  k s
k z k z v  c 
y
y z
x
 x z
where
c  cos  , s  sin  , v  1  cos 
T
kˆ  k , k , k 
x
y
z
1
EGGN 512
Computer Vision
1. Describe what kind of image the following Matlab code will generate, and draw a
sketch.
I=zeros(128,128);
for i=1:128
for j=1:128
if (i-64)*(i-64) + (j-64)*(j-64) < 40*40
I(i,j)=j;
else
I(i,j)=i;
end
end
end
Solution:
The background increases from dark at the top of the 128x128 image to light at the bottom of the
image. In the middle is a circle of radius 40, whose intensity increases from left to right.
2. Write a Matlab program that will generate an image of a checkerboard, consisting of
black and white squares in a 8x8 pattern. Each square is 10x10 pixels.
Solution:
There are many possible ways to do this. Here is one:
N = 10;
% Size of each square, in pixels
I = false(8*N,8*N);
for i=1:2*N:8*N
I(:, i:i+N-1) = true;
end
I = xor(I, I');
imshow(I, []);
2
EGGN 512
Computer Vision
3. A digital camera is modeled as a pinhole camera with focal length f. It has 512x512
sensor elements (pixels), where the center pixel (x,y) = (256,256) corresponds to the
optical axis. A point P has 3-D coordinates (1m, 2m, 8m) in camera coordinates, and
projects to pixel (x,y) = (356,456). Find the pixel projection of point Q, if Q has 3-D
coordinates (-3m, -1m, 16m) in camera coordinates.
Solution:
We can solve for focal length since we know from point P, (356-256) = f (1 m/ 8 m). So f = 800
pixels.
For Q:
(x-x0) = f X/Z = (800) (-3)/(16) = -150, or x = -150+256 = 106
(y-y0) = f Y/Z = (800) (-1)/(16) = -50, or y = -50+256 = 206
4. Correlate the horizontal Sobel filter with the image below. You may assume that the
image is padded with zeros beyond the visible boundaries of the image.
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
Solution:
The horizontal Sobel filter is
-1 0
+1
-2 0
+2
-1 0
+1
Correlation is defined as g ( x, y) 
m /2
n /2
 
h( s, t ) f ( x  s, y  t )  h  f . We will get
s  m /2 t  n /2
0
0
0
0
0
0
0
0
3
EGGN 512
Computer Vision
0
0
0
0
0
0
0
0
0
1
1
0
0
-1
-1
0
0
3
3
0
0
-3
-3
0
0
4
4
0
0
-4
-4
0
0
4
4
0
0
-4
-4
0
0
4
4
0
0
-4
-4
0
0
3
3
0
0
-3
-3
0
5. A square pixel camera looks down at a workbench. Points P1 and P2 have (x,y) image
coordinates (100,100) and (100,200), respectively. The locations of points P1 and P2 on
the X,Y plane of the workbench are (500mm, 300mm) and (1000mm, 300mm),
respectively. What is the X,Y location of point P3 on the workbench if its image
coordinates are (250,400)?
We will treat this as a rotation, followed by a scaling, followed by a translation.
The rotation angle is w – i = 0 – 90 = -90.
Next determine the scale factor: The distance between P1 and P2 is 100 pixels in the image, and
500 mm on the workbench. So the scale s = 500 mm/100 pixels = 5 mm/pixel.
 x w   1 0 x0  s 0 0  cos 
  


 y w    0 1 y 0  0 s 0  sin 
 1   0 0 1  0 0 1  0
  


 sin 
cos 
0
0  xi 
 
0  yi 
1  1 
x w  xi s cos   yi s sin   x0
y w  xi s sin   yi s cos   y 0
Using the coordinates of P1:
500 mm = (100 pix)(5 mm/pix) 0 – (100 pix)(5 mm/pix) (-1) + x0 = 500 mm + x0
300 mm = (100 pix)(5 mm/pix) (-1) + (100 pix)(5 mm/pix) (0) + y0 = -500 mm + y0
or
x0 = 0, y0 = 800 mm
For P3:
xw = (250 pix)(5 mm/pix) 0 – (400 pix)(5 mm/pix) (-1) + 0 = 2000 mm
4
EGGN 512
Computer Vision
yw = (250 pix)(5 mm/pix) (-1) + (400 pix)(5 mm/pix) 0 + 800 mm = -450 mm
6. A sphere of radius = 1 meter is projected onto an image. The camera has a focal length
of 10 mm, and the each pixel corresponds to 0.01 mm on the image plane. The sphere
projects to a circle of radius = 20 pixels on the image plane. How far away is the sphere
from the camera (ie., what is its Z coordinate)?
Solution:
The sphere has a projected radius of 20 pixels or 0.2 mm. By similar triangles, 0.2 mm/10 mm
= 1 meter / Z, or Z = 50 meters
7. A camera is mounted on the end effector of a robot arm as shown below. The end
effector coordinate system {E} has its Z axis pointing up, its Y axis pointing to the right
in the figure, and the X axis pointing out of the page. The origin of the camera {C} is
located at a position of (X,Y,Z) = (0, 10 cm, 5 cm) with respect to {E}. The X axis of the
camera is aligned with the X axis of the end effector. The Z axis of {C}is tilted down at
an angle of 45 degrees with respect to the Y axis of {E}. Write the 4x4 transformation
matrix relating the pose of the camera with respect to the end effector, ECT .
{C}
y
z
z
{E}
y
Solution:
The columns of the rotation matrix CE R are the unit vectors of {C} with respect to {E}.
The X axis of the camera is [ 1, 0, 0 ]T with respect to {E}.
The Y axis of the camera is [ 0, -0.707, -0.707 ]T with respect to {E}.
The Z axis of the camera is [ 0, 0.707, -0.707 ]T with respect to {E}.
So
0
0
0
1


 0  0.707 0.707 10 
E
CT  
0  0.707  0.707 5 


0
0
1 
0
5
EGGN 512
Computer Vision
It is also possible to do this one by plugging into the formula for the rotation matrix for XYZ
angles … we have a single rotation of -135 degrees about the x axis.
8. Image A is modified by the affine transform below. Sketch image “B”.
 xB   1 0.1 10  xA 
  
 
20  y A 
 yB    0.2 1
1  0

0
1 
  
 1 
Image A (the x,y coordinates of the corners of the square are given):
10,10
10,50
50,10
50,50
The corners of the square map as follows:
xB =
xA – 0.1 yA + 10
yB = 0.2 xA +
yA + 20
So
(10,10) -> (10-1+10, 2+10+20) = (19, 32)
(10,50) -> (10-5+10, 2+50+20) = (15, 72)
(50,10) -> (50-1+10, 10+10+20) = (59, 40)
(50,50) -> (50-5+10, 10+50+20) = (55, 80)
Image B
19,32
15,72
59,40
55,80
6
EGGN 512
Computer Vision
9. The perspective projection matrix for a camera is given below. This matrix models
both the intrinsic parameters of the camera and the extrinsic parameters (i.e., its pose
in the world).
 0 100 500 1500 


M   500 100 0
0 
 0
1
0
10 

A point is located at (X=1, Y=0, Z=1) in world coordinates. What image point does it
project to?
Solution:
p = MP = [2000; 500; 10]. We divide by the third element to get the x,y image coordinates:
x = 2000/10 = 200
y = 500/10 = 50
10. A pinhole camera (with focal length = 1) observes a flat wall. The camera is oriented
with its optical axis 45 degrees from the normal to the wall. The distance to the wall
(along the optical axis) is 10 meters. A top-down view is shown below.
d=10 m
=45°
The camera points directly at the origin of the wall plane. The X axis of the wall points
to the right along the wall, and the Y axis points down.
The mapping of points from the wall plane to the image plane can be described by a
projective transform, or homography, such that
 x1   a11 a12 a13  X Wall 
  


 x2    a21 a22 a23  YWall  , ximg  x1 / x3 , yimg  x2 / x3
 x  a


 3   31 a32 a33  1 
Which of the following matrices is the correct projective transform?
0 10 
1 0 0
 0.707 0 0 
 .707
0 1 1 








1 0  (c)  0 .707 0  (d)  1 0 0 
(a)  0 1 0  (b)  0
0 0 1
 0.707 0 10 
 0
 0 0 10 
0
1 







7
EGGN 512
Computer Vision
Solution:
First transform the wall points to the camera’s coordinate system,
C
W
 CR
H   W
 0
Now,
C
W
C
Cam
Cam
P  Wall
H Wall P , where
t Worg 
.
1 
R is the rotation matrix that describes the orientation of frame {W} with respect to
frame {C} (see slide 6 of Lecture 3). The two frames differ by a rotation about the Y axis.
Wz
Wy
Wx
Cz
Cy
Cx
The rotation is -45 degrees (see slide 9 of Lecture 4): Start with the {W} frame aligned with the
{C} frame. Point your right thumb in the direction of Wy. Then rotate the {W} frame until you
get to the desired orientation. You will have to rotate -45 degrees; i.e., Y = -45°.
Wz
Cz
The arrow shows the
direction of rotation for
a positive angle
Wx
+Y
Cx
The resulting rotation matrix is
 cos  Y 0 sin Y   0.707 0  0.707 

 

C
0
1
0  0
1
0 
W R 
  sin  0 cos    0.707 0 0.707 
Y
Y 



This makes sense because the columns of the rotation matrix are the unit vectors of the {W}
frame, expressed in the representation of the {C} frame. So the first column is the X axis of
8
EGGN 512
Computer Vision
{W}. As you can see in the figure, it points in the +X and +Z direction in the {C} frame. The
third column is the Z axis of {W}, and it indeed points in the –X and +Z direction in the {C}
frame.
The full transformation matrix is a rotation about the Y axis by 45 degrees, plus a translation of
10.
 0.707 0 0.707 0 


0
1
0
0
Cam

Wall H 
 0.707 0 0.707 10 


0
0
1
 0
So
XCam = (0.707) XWall – (0.707) ZWall
YCam = YWall
ZCam = (0.707) XWall + (0.707) ZWall + 10
But the wall is a plane, so all its Z values are zero:
XCam = (0.707) XWall
YCam = YWall
ZCam = (0.707) XWall + 10
Under image perspective projection,
ximg = f XCam / ZCam = (0.707) XWall / ( (0.707) XWall + 10 )
yimg = f YCam / ZCam =
YWall / ( (0.707) XWall + 10 )
We can accomplish this with the matrix
 x1   0.707 0 0  X Wall 
  


1 0  YWall  ,
 x2    0
 x   0.707 0 10  1 
 3 


ximg  x1 / x3 , yimg  x2 / x3
11. Write MATLAB code to shrink the size (ie., total number of pixels) of an image I by a
factor of four by subsampling. Assume that the dimensions of I are 512x512. (Note for this problem, you are not allowed to use the MATLAB function “imresize”).
Solution:
for i=1:512
for j=1:512
I2(i/2, j/2) = I(i,j);
end
end
9
EGGN 512
Computer Vision
or
for i=1:256
for j=1:256
I2(i, j) = I(2*i,2*j);
end
end
or
I2 = I(1:2:end, :);
I3 = I2(:, 1:2:end);
12. Image A is mapped to image B using an affine transformation. A square in image A is
mapped to parallelogram in image B. In image A, the square has dimension LxL, with
its top left corner of the square is at location (L,L). In image B, the parallelogram has
the dimensions shown. Its top left corner is also at location (L,L). Give the affine
transformation that maps A to B.
A
B
L
L
L
L
L/2
Solution:
We want to find the elements of the matrix aij such that
 xB   a11 a12 t x  x A 
  
 
 yB    a21 a22 t y  y A 
1  0

0 1 
  
 1 
The corners of the square in image A are
(L,L) (2L,L)
(L,2L) (2L,2L)
The corresponding points in the image B are:
(L,L) (2L,L)
10
EGGN 512
Computer Vision
(3L/2,2L) (5L/2,2L)
Obviously yB = yA, so a21 = 0, a22 = 1, ty = 0.
To find the rest of the values, write the equations for xB = a11 xA + a12 yA + tx
Writing down this equation at each tiepoint yields
L = a11 (L) + a12 (L) + tx
2L = a11 (2L) + a12 (L) + tx
3L/2 = a11 (L) + a12 (2L) + tx
Solving for these yields a11 = 1, a12 = 1/2, tx = -L/2
The affine transformation is
 xB   1 1/ 2  L / 2  x A 
  
 
0  y A 
 yB    0 1
 1  0 0

1 
  
 1 
11