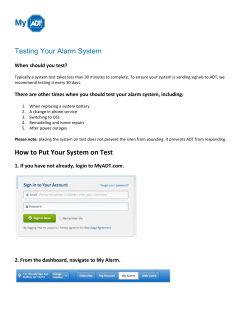
Statistics: Sample Exam 2 Solution Chapters 4 & 5: Probability, Probability Distribution 1. A simple event is an outcome or event that cannot be further broken down. 2. A sample space is a procedure that consists of all possible sample events. 3. If two events are mutually exclusive, the probability that both will occur is 0 P  A  B  0 4. The probability of an event is always between 0 and 1 0 ≤ P(A) ≤1 5. The sum of probabilities of all final outcomes of an experiment is always 1 6. The number of Combinations of n items selected n at a time is 1 nCn = n! / n! (n-n)! nCn = n! / n! (0!) *0! = 1 nCn = n! / n! (1) nCn = 1 7. The number of Permutations of n items selected 0 at a time is 1 nP0 = n! / (n-0)! nP0 = n! / n! nP0 = 1 8. The sample space for tossing 5 coin s consists of how many outcomes? 32 outcomes each coin has 2 outcomes: 25 = 32 9. A quiz consists of 3 true-false questions, how many possible answer keys are there? 8 possible answer keys 23 = 8 Although order is important, values can repeat one another (ex: true, true, true) 10. A pizza parlor offers 10 different toppings; how many four topping pizzas (different toppings) are possible? 210 four topping pizzas are possible order is not important  combination is used 10C4 = 10! / 4! (10-4)! = 10! / 4! X 6! = 10 x 9 x 8 x 7 x 6! / 4 x 3 x 2 x 1 x 6! = 210 11. How many 6-letter code words can be made from the 26 letters of the alphabet if no letter can be used more than once in the code word? 165, 765, 600 6-letter code words can be made order is important, no letter can be used more than once  permutation is used 26P6 = 26! / (26-6)! = 26! / 20! = 26 x 25 x 24 x 23 x 22 x 21 x 20! / 20! = 165, 765, 600 1 A random sample of 100 people was asked if they were for or against the tax increase on rich people. Of 60 males 45 were in favor, of all females 22 were in favor. Write the contingency table and answer the following questions. (Hint: Make up a table like Table 4-1 of page 152.) If one person is selected at random, find the probability that: Male Female total For tax increase on rich people Against tax increase on rich people Total 45 15 60 22 18 40 67 33 100 12. This person favors the tax increase on rich people. P(A) = n(A) / n(S) P(A) = 67/100 (or 0.67) 13. This person is a female. P(F) = n(F) / n(S) P(F) = 40/100 = 2/5 (or 0.4) 14. This person opposes the tax increase on rich people given that the person is a female. P(A|F) = P(A ∩ F) / P(F) P (A|F) = n(A ∩ F) / n(F) P(A |F)= 18/40 = 9/20 (or 0.45) 15. This person is a male given that he favors the tax increase on rich people. P(M|T) = P(M ∩ T) / P(T) P(M|T) = n(M ∩ T) / n(T) P(M|T) = 45/67 (or 0.6716) 16. This person is a female and favors the tax increase on rich people. P (F∩ T) = 22/100 = 11/50 (or 0.22) 17. This person opposes the tax increase on rich people or is a female. P(A U F) = P(A) + P(F) - P(A∩F) P(A U F) = n(A)/n(S) + n(F)/n(S) – n(A∩F)/n(S) P(A U F) = 33/100 + 40/100 – 18/100 = 55/100 = 11/20 (or 0.55) 18. Are the events “females” and opposes the tax increase on rich people independent? Explain. Events “females” and opposite the tax increase on rich people is dependent because occurrence of one of the events does affect the other event. Proof: P (A |F) = 18/40 P (A) = 67/100 19. Are they mutually exclusive? Explain. They are not mutually exclusive because a person can be both female and oppose the tax increase on rich people. Those two events are not disjoint. Proof: P(A∩F) = 18/100 20. Find the probability of getting the outcome of “Tails and 2” when a coin is tossed and a die is rolled. 2 P(A∩B) = P(A) x P(B) ½ x 1/6 1/12 (or 0.0833) In a game, you pay 60 cents to select a sequence of 4 digits such as 1234. If you win by selecting the same sequence of 4 digits that are drawn, you collect $3,000. 21. How many different selections are possible? n = number of digits = 10 10 possible numbers in 4 places (numbers can repeat) 104 = 10,000 22. What is the probability of winning? 1/10,000 23. If you win, what is your net profit? net profit = money gained – investment = 3000 – 0.60 = $2999.40 24. Write the Probability Distribution of Net Profit if you win. probability distribution of net profit if I win: 0.29994 Event Lose x -0.60 P(x) 9,999/10,000 (0.9999) 1/10,000 (0.0001) win +2999.40 25. Find the expected value. E = μ = ∑(x P(x)) -0.3 x P(x) -0.59994 0.29994 26. A box consists of 14 red and 36 blue markers. If we select 3 different markers randomly, a. What is the probability that they are all red? (with replacement) n(total) = 14 + 36 = 50 P(R) = n(R)/n(S) = 14/50 = 7/25 (7/25)3 = 343/15,625 = 0.021952 b. What is the probability that they are all red? (without a replacement) Draw a tree diagram and label each branch. (14/50) x (13/49) x (12/48) = 7/25 x 13/49 x ¼ = 13/700 (or 0.0186) If the probability of winning the race is 5/12, 27. What is the probability of losing the race? 1 – probability of winning 1 – 5/12 = 7/12 28. What are odds against winning? P(A’)/P(A) = (7/12)/(5/12) = 7/5 (or 7:5, 1.4) 3 29. If the pay off odd is listed as 6:1, how much profit do you make if you bet $10 and you win? (10 x 6) = 60 60 – 10 = 50 $50 It is known that 90% of managers of all companies suffer from job related stress. What is the probability that in a sample of 10 managers, 30. Exactly 8 suffer from job related stress. n = 10, x = 8, p = 0.9, q = 0.1 P(x) = n! /x! (n-x)! x px x qn-x P(8) = 10! /8! 2! X (0.9)8 x (0.1)2 P(8) = 45 x (0.9)8 x (0.1)2 P(8) = 0.1937 31. At most 2 suffer from job related stress. x ≤2 (x = 0,1,2) P(x) = n! /x! (n-x)! x px x qn-x P(0) + P(1) + P(2) P(0) = 10!/0! 10! X (0.9)0 x (0.1)10 P(0) = 1 x 1 x 0.110 P(1) = 10!/1! 9! X 0.91 x (0.1)9 P(1) = 10 x 0.9 x 0.19 P(1) = 0.000000009 P(2)= 10!/2! 8! X (0.9)2 x (0.1)8 P(2) = 45 x (0.9)2 x (0.1)8 P(2) = 0.0000003645 P(0) + P(1) + P(2) = 0.0000003746 or 3.746 x 10-7 32. At least 3 suffer from job related stress. x ≥3 (x=3,4,5,6,7,8,9,10) P(x≥3) = P(3) + P(4) + P(5) + P(6) + P(7) + P(8) + P(9) + P(10) = 1 –[ (P(0) + P(1) + P(2)] =1 – 0.0000003746 = 0.999999625 33. Find the expected value. E=μ=nxp E = 10 x 0.9 = 9 34. Find the standard deviation. σ2 = n x p x q σ2 = 10 x 0.9 x 0.1 = 0.9 4 σ = √0.9 σ = 0.9487 35. Would it be unusual to claim that at least 7 managers from this sample suffer from job related stress? range rule of thumb: μ ± 2σ 9 ± 2(0.9487) usual minimum: 7.1026 usual maximum: 10. 8974 7  (7.1026,10.8974)  Unusual 36. Find the probability of a couple having at least one girl among 3 children. n = 3, x ≥1, p = q = ½ x = 1,2,3 P(1) + P(2) + P(3) = 1 – P(0) P(x) = n! /x! (n-x)! x px x qn-x P(0) = 3! /0! 3! X (0.5)0 x (0.5)3 P(0) = 1 x (0.5)3 P(x≥1) = 1 – 0.53 = 1 – 0.125 = 0.875 (or 7/8) If an alarm clock has a 0.9 probability of working on any given morning. 37. What is the probability that it will not work? 1 – 0.9 = 0.1 (or 10 percent) 38. What is the probability that 2 such alarm clocks will not work? 0.1 x 0.1 = 0.01 there is the probability of 1% that 2 such alarm clocks will not work. 39. What is the probability of being awakened if you have 2 such alarm clocks? Probability of being awakened = 1 – probability of not being awakened 1 – 0.01 = 0.99 the probability of being awakened if you have 2 such alarm clocks is 99%. or P(A U B) = P(A) + P(B) – P(A∩B) = 0.9 + 0.9 – (0.9 x 0.9) = 0.99 5