1. No category

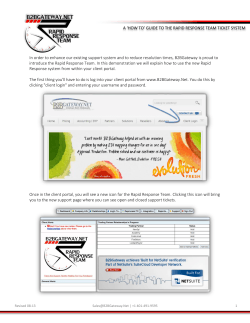
Math 46 - Final Exam Sample Packet A
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Find the slope of the line.
1) 11x + y = 9
1
A) m = 11
1)
B) m = 11
11
C) m =
9
D) m = -11
2) -x + 5y = 30
2)
1
A) m = 5
1
B) m =
5
C) m = -1
D) m = 5
Find the slopes of the lines that are (a) parallel to and (b) perpendicular to the line passing through the pair of points.
3) (8, -6) and (4, 7)
3)
4
13
13
4
A) (a) ; (b)
B) (a)
; (b) 13
4
4
13
C) (a) -
13
4
; (b)
4
13
D) (a) -
13
13
; (b)
4
4
Use the slope-intercept form to graph the equation.
4) y = 2x + 4
4)
y
10
5
-10
-5
10 x
5
-5
-10
A)
B)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
5
-5
-5
-10
-10
Appendix A - 1
10 x
C)
D)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
10 x
5
-5
-5
-10
-10
Write an equation of the line with the given slope, m, and y-intercept (0, b).
5) m = 7 , b = -3
3
A) y = - 7 x + 3
3
B) y = 7 x - 3
3
C) y = - 7 x - 3
3
5)
D) y = 7 x + 3
3
Find an equation of the line through the pair of points. Write the equation in the form Ax + By = C.
6) (-6, -9) and (-4, 0)
A) -3x + 4y = 12
B) 3x - 4y = 12
C) -9x - 2y = -36
D) 9x - 2y = -36
Find an equation of the line described. Write the equation in slope-intercept form if possible.
7) Through (-10, -57) and (3, 8)
1
1
A) y = x - 55
B) y = - x - 59
C) y = 5x - 7
D) y = -5x - 107
5
5
Solve. Assume the exercise describes a linear relationship.
8) A faucet is used to add water to a large bottle that already contained some water. After it has
been filling for 3 seconds, the gauge on the bottle indicates that it contains 10 ounces of water.
After it has been filling for 11 seconds, the gauge indicates the bottle contains 26 ounces of water.
Let y be the amount of water in the bottle x seconds after the faucet was turned on. Write a
linear equation that models the amount of water in the bottle in terms of x.
17
A) y = 1 x +
B) y = 2x + 4
C) y = -2x + 16
D) y = 2x + 15
2
2
Simplify the expression.
4
4x3
9)
y2
A)
257x7
y6
7)
8)
9)
B)
4x12
y8
C)
256x12
y2
D)
256x12
y8
10) (-3z2)(5z3)
A) -15z5
6)
10)
B) 1125z5
C) -15z6
Appendix A - 2
D) 15z6
Simplify the expression. Write the result using positive exponents only.
-2
xy 4
11)
x3y
A)
12)
1
5
x y9
B)
1
C)
x8y 10
x4
y6
11)
D)
y6
x4
13r-1(r-4)2
14(r-1)3
A)
13r6
14
12)
B)
13r5
14
C)
13
14r5
D)
13
14r6
Perform the indicated operation.
13) (7n6 - 19n3 - 19) - (3n6 + 11n3 - 3)
13)
A) 4n6 - 30n3 - 22
B) 4n6 - 30n3 - 16
C) 4n6 - 16n3 - 22
D) -42n9
Simplify the following by combining like terms.
14) 7r + 12r6 - 3r6 + 12r
14)
A) 28r6
B) 28r
C) 19r + 9r6
D) cannot be simplified
Factor the polynomial completely. If the polynomial cannot be factored, write "prime."
15) y 2 - 4y - 21
A) (y - 21)(y + 1)
B) prime
C) (y - 7)(y + 3)
15)
D) (y + 7)(y - 3)
16) x2 + 4xy - 21y 2
A) (x - 7y)(x + 3y)
B) prime
C) (x - 7y)(x + y)
D) (x + 7y)(x - 3y)
17) 4t2 + t - 5
A) (4t + 1)(t - 5)
B) (4t + 5)(t - 1)
C) (4t - 5)(t + 1)
D) (4t - 1)(t + 5)
16)
17)
18) xy 2 + 6y 2 - 4x - 24
18)
A) (x + 6)(y - 2)2
B) (x + 6)(y 2 - 4)
C) (x - 6)(y + 2)(y - 2)
D) (x + 6)(y + 2)(y - 2)
19) -yz5- y 5z
19)
A) -yz(y 4 + z4)
B) -yz(y - z)(y 4 + yz + z4)
C) -yz(y + z)(y 4 - yz + z4)
D) -yz(y - z)(y - z)
Appendix A - 3
Solve the equation.
20) 9t3 - 64t = 0
20)
A) 0
B) -
21) 17x2 = 8x
A) - 8 , 0
17
8 8
,
3 3
8 8
, ,0
3 3
C) -
D)
8
3
21)
B) 0, 8
17
C) - 17 , 0
8
D) 0, 17
8
Solve.
22) The sum of two numbers is 16 and the sum of their squares is 146. Find the numbers.
A) 10 and 6
B) 11 and 5
C) 13 and 3
D) 12 and 4
Multiply or divide as indicated.
2x + 6y
∙ x + 3y
23)
3
x2 + 6xy + 9y 2
24)
23)
A)
2x2 + 18xy + 18y 2
3x2 + 18xy + 27y 2
B)
2x + 6y
3(x + 3y)
C)
4
18xy
D)
2x2 + 18xy
3x2 + 18xy + 27y 2
(x + 3)2 ÷ x2 - 9
x- 3
3x - 9
A)
24)
3(x + 3)
x- 3
B)
(x + 3)3
3(x - 3)
C)
(x + 3)2
(x - 3)2
D)
6(x2 + 9)
x2 - 9
Simplify the expression.
(x2)4
25)
(3x)3
A)
25)
x11
27
B)
x5
27
C)
x5
3
D)
x3
27
Perform the indicated operation. Simplify if possible.
8a + 6b - 8a - 6b
26)
2
2
A) 36b
27)
x
x2 + 7x - 44
A) x + 11
B) 0
-
22)
26)
C) 8a
D) 6b
4
27)
x2 + 7x - 44
B) x - 4
C)
1
2(x + 11)
Appendix A - 4
D)
1
x + 11
Find the perimeter.
28)
28)
(x2 + 3x + 9) units
(x2 + 3x + 9)
units
A) (4x2 + 12x + 36) units
B) (x2 + 6x + 18) units
D) (x4 + 12x2 + 36) units
C) (x4 + 6x2 + 18) units
Factor the sum or difference of two cubes.
29) t3 + 64
29)
A) (t - 4)(t2 + 4t + 16)
B) (t + 4)(t2 + 16)
C) (t + 4)(t2 - 4t + 16)
D) (t - 64)(t + 1)(t - 1)
Find an equation of the line.
30) Perpendicular to y = 6, through (8, 11)
A) y = 11
B) x = 8
30)
C) x = -
Appendix A - 5
1
8
D) y = -
8 + 119
x
5
5
!
Math 46 - Final Exam Sample Packet B
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Solve.
1) The house numbers of two adjacent homes are two consecutive even numbers. If their sum is
326, find the house numbers.
A) 162, 324
B) 161, 163
C) 162, 164
D) 163, 165
Solve the formula for the specified variable.
2) A = P + PRT
for R
A
A) R =
B) R = PT
T
A-P
3) S = 2πrh + 2πr2
2)
C) R = P - A
PT
D) R = A - P
PT
for h
A) h = S - r
1)
3)
B) h = S - 1
2πr
2
C) h = S - 2πr
2πr
D) h = 2π(S - r)
Solve. If needed, round money amounts to two decimal places and all other amounts to one decimal place.
4) A store is advertising 20% off sale on everything in the store. Find the discount of a painting that
4)
regularly sells for $280.
A) $5.60
B) $274.40
C) $56.00
D) $224.00
Multiply.
5) 7y 2(5y 2 - 5y + 8)
A) 35y 4 - 35y 2 + 56
C) 35y 4 - 35y + 56
5)
B) 12y 4 + 2y + 15
D) 35y 4 - 35y 3 + 56y 2
Solve. If needed, round money amounts to two decimal places and all other amounts to one decimal place.
6) A store is advertising 15% off sale on everything in the store. Find the sale price of a painting
6)
that regularly sells for $260.
A) $2561.00
B) $39.00
C) $3.90
D) $221.00
7) Because of budget cutbacks, MaryAnn was required to take a 18% pay cut. If she earned $28,000
before the pay cut, find her salary after the pay cut.
A) $27,949.60
B) $22,960
C) $27,496
D) $2296
7)
8) A chemist needs 100 milliliters of a 76% solution but has only 55% and 85% solutions available.
Find how many milliliters of each that should be mixed to get the desired solution.
A) 70 ml of 55%; 30 ml of 85%
B) 40 ml of 55%; 60 ml of 85%
C) 60 ml of 55%; 40 ml of 85%
D) 30 ml of 55%; 70 ml of 85%
8)
9) The radiator in a certain make of car needs to contain 50 liters of 40% antifreeze. The radiator
now contains 50 liters of 20% antifreeze. How many liters of this solution must be drained and
replaced with 100% antifreeze to get the desired strength?
A) 12.5 L
B) 25 L
C) 16.7 L
D) 20 L
9)
Appendix B - 1
Solve the problem.
10) Sue took her collection of nickels and dimes to deposit in the bank. She has five fewer nickels
than dimes. Her total deposit was $55.40. How many dimes did she deposit?
A) 376 dimes
B) 371 dimes
C) 737 dimes
D) 366 dimes
10)
Solve.
11) Jeff starts driving at 65 miles per hour from the same point that Lauren starts driving at 40 miles
per hour. They drive in opposite directions, and Lauren has a half-hour head start. How long
will they be able to talk on their cell phones that have a 480-mile range?
4
8
17
16
A) 4 hr
B) 4
hr
C) 4
hr
D) 4
hr
7
21
30
21
Solve the problem.
12) Devon purchased tickets to an air show for 7 adults and 2 children. The total cost was $92. The
cost of a child's ticket was $8 less than the cost of an adult's ticket. Find the price of an adult's
ticket and a child's ticket.
A) adult's ticket: $13; child's ticket: $5
B) adult's ticket: $14; child's ticket: $6
C) adult's ticket: $12; child's ticket: $4
D) adult's ticket: $11; child's ticket: $3
Multiply.
13) (y + 6)(y + 7)
A) 2y 2 + 42
C) 2y + 42
A) (-∞, -2)
-4
-3
-2
-1
0
1
-4
-3
-2
-1
0
1
-4
-3
-2
-1
0
1
-4
-3
-2
-1
0
1
B) [-2, ∞)
-5
C) (-∞, -2]
-5
D) (-2, ∞)
-5
12)
13)
B) y 2 + 13y + 42
Solve the inequality. Graph the solution set and write it in interval notation.
14) -2(4x - 7) < -10x + 10
-5
11)
Appendix B - 2
D) y 2 + 13y + 13
14)
15) 15x - 35 > 5(2x - 11)
15)
A) [-4, ∞)
-7
-6
-5
-4
-3
-2
-1
-6
-5
-4
-3
-2
-1
-6
-5
-4
-3
-2
-1
-6
-5
-4
-3
-2
-1
B) (-∞, -4]
-7
C) (-∞, -4)
-7
D) (-4, ∞)
-7
Find the domain and the range of the relation.
16) {(7, 3), (7, -7), (7, -5)}
A) domain: {-7, -5, 3} ; range: {7}
C) domain: {3, 7} ; range: {-7, -5}
16)
B) domain: {7} ; range: {-7, -5, 3, 7}
D) domain: {7} ; range: {-7, -5, 3}
Find the domain of the function.
17) g(x) = 2
x - 15
17)
A) (-∞, 15) ∪ (15, ∞)
C) (-∞, ∞)
B) (-∞, 2) ∪ (2, ∞)
D) (-∞, -15) ∪ (-15, ∞)
Evaluate the function.
18) Find f(11) when f(x) = 6x - 11
A) -55
B) 55
18)
C) 56
Solve the system of equations by the substitution method.
19) -5x + y = -26
-6x - 3y = -6
A) (5, -7)
B) (-6, 4)
Solve the system of equations by the addition method.
20) x + 3y = 11
-6x + 2y = -6
A) (1, 4)
B) (2, 3)
21)
-2x + 2y = -5
4x - 4y = 10
A) (-2, 2)
C) (0, 0)
D) 77
19)
C) (4, -6)
D) no solution
20)
C) no solution
D) (-2, 4)
21)
B) no solution
D) infinite number of solutions
Appendix B - 3
Multiply.
22) (z - 5)(z2 + 5z - 3)
A) z3 + 22z - 15
22)
B) z3 - 10z2 - 28z + 15
D) z3 - 28z + 15
C) z3 + 10z2 + 28z - 15
23) (6y + x)(6y - x)
A) 12y 2 - x 2
B) 36y 2 + 12xy - x 2
23)
C) 36y 2 - x 2
D) 36y 2 - 12xy - x 2
Find the product and simplify.
5x3y 3 ∙ y 9
24)
-45xy 12
A)
25)
26)
x3
-9y
24)
B)
x2y
-9
C)
x3
-9
D)
x2
-9
8p - 8 ∙ 8p2
p
9p - 9
25)
A)
72p2 + 144p + 72
8p3
B)
9
64p
C)
64p
9
D)
64p3 - 64p2
9p2 - 9p
x2 + 10x + 21 ∙ x2 + 16x + 64
x2 + 15x + 56 x2 + 11x + 24
A)
x+3
x+8
26)
B)
1
x+8
C)
x+8
x+8
D) 1
Find the quotient and simplify.
3x2 ÷ x3
27)
5
15
A)
28)
9x2
x3
27)
B)
9
x
C)
x
9
D)
45x2
5x3
m2 - n2 ÷
m
m +n
2
m - mn
A) (m + n)2
28)
B) (m - n)2
C) (m - n)(m + n)
Appendix B - 4
D) (m + n)
29)
(x - 6)(x + 7) ÷ 5x - 30
3x
15x8
A) x8(x + 7)
30)
29)
B)
x7(x + 7)
5
C) x7(x + 7)
p2 - 9p + pq - 9q ÷ p - 9
4p - 4q
6p2 - 6q 2
30)
2
3
B)
C) 1
D)
A)
D) 5x7(x + 7)
4(p2 - 9p + pq - 9q)
6(p + q)(p - 9)
(p - 9)2
24(p - q)2
Appendix B - 5
!
Math 46 - Final Exam Sample Packet C
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Simplify the expression.
1) (-9)0 + (-14)0
A) 0
1)
B) 2
C) -2
D) -23
Simplify.
2)
2)
x
6
7
x+ 4
A) 42x(x + 4)
B)
x(x + 4)
42
C)
x+ 4
42x
D)
6x
7(x + 4)
3)
3)
x
4
7
x+ 7
A)
x(x + 7)
28
B)
4x
7(x + 7)
C)
4) If Q(x) = 4x2 + 3x + 2, find Q(-1).
A) 1
B) -5
x+ 7
28x
D) 28x(x + 7)
4)
C) 9
D) 3
Perform the division.
-18x6 - 15x4 - 12x2
5)
-3x4
A) 6x2 + 5 + 4
x
5)
B) 6x + 5 + 4
x2
C) 6x2 + 5 + 4
x2
Perform the indicated operation. Simplify if possible.
x
6
6)
x2 - 16 x2 + 5x + 4
D) 6x + 5 + 4
x
6)
A)
x2 - 5x + 24
(x - 4)(x + 4)(x + 1)
B)
x2 - 5
(x - 4)(x + 4)(x + 1)
C)
x2 + 5x + 24
(x - 4)(x + 4)(x + 1)
D)
x2 - 5x + 24
(x - 4)(x + 4)
Appendix C - 1
Write the number in standard notation.
7) 1.59 × 10 -4
A) 0.000159
7)
B) -159,000
C) 0.0000159
D) -0.000159
Solve the inequality. Graph the solution set.
8) |x + 16| < 17
8)
A) (-∞, 1)
-15
-10
-5
0
5
10
15
20
B) (-33, 1)
-30
-25
-20
-15
-10
-5
0
5
C) (-1, 33)
0
5
10
15
20
25
30
35
-50
-45
-40
-35
-30
-25
-20
-15
D) (-∞, -33)
Find an equation of the line. Write the equation in standard form.
9) Through (2, 3); perpendicular to 2x - 5y = 2
A) 2x + 5y = 16
B) 2x - 5y = 16
C) 5x + 2y = 16
9)
D) 5x - 2y = 16
Solve the equation.
2(8 - x) = -x
10)
3
A) -2
11)
10)
B) -16
C) 2
D) 16
x = -2x + 2x - 3
2x + 2 4x + 4
x+1
A) 3
11)
B)
3
2
C) no solution
D) -3
C) p = -4
D) p = -6
Solve.
12) -3(2p + 5) - 10 = -2(p + 6) + 3
A) p = 6
12)
B) p = 4
13) Linda and Dave leave simultaneously from the same starting point biking in opposite directions.
Linda bikes at 7 miles per hour and Dave bikes at 8 miles per hour. How long will it be until
they are 20 miles apart from each other?
1
3
5
A) 20 hr
B) 1 hr
C) hr
D)
hr
3
4
14
Appendix C - 2
13)
Subtract as indicated.
6 4
14) 9 7
A)
14)
2
3
B)
2
9
C)
2
63
D)
Find the slope of the line that passes through the given points.
15) (9, 1) and (2, -7)
6
7
8
A) B)
C) 11
8
7
15)
D)
Solve the compound inequality. Graph the solution set.
16) 6x - 4 < 2x or -4x ≤ -12
1
A) (-∞, 1) ∪ [3, ∞)
B) (1, 3)
1
2
2
3
3
4
8
7
16)
4
5
2
21
5
6
6
7
7
8
8
C) [1, 3]
1
2
3
4
5
6
7
D) ∅
-3
-2
-1
0
1
2
3
8
Multiply.
17) (x - 6)(x2 - 8)
A) x2 - 14x + 48
C) x3 - 6x2 - 8x + 48
17)
B) x3 - 8x2 - 6x + 48
D) -6x2 + x + 48
Appendix C - 3
Solve the system of equations by graphing.
18) y = -x - 3
y = 2x + 3
18)
y
6
4
2
-6
-4
-2
2
4
6
x
-2
-4
-6
A) no solution
B) (-2, -1)
C) (1, -2)
D) (-2, 1)
Perform the indicated operation.
19) (8n7 - 6n5 - 19) - (2n7 + 13n5 - 5)
19)
A) 6n7 - 19n5 - 24
B) -27n12
C) 6n7 - 19n5 - 14
D) 6n7 - 4n5 - 24
Factor out the GCF, greatest common factor, from the polynomial.
20) 80m7 + 64m5 + 24m3
20)
A) 8m3(10m4 + 8m2 + 3)
B) -m3(-80m4 + 64m2 - 24)
C) m3(80m4 + 64m2 + 24)
D) 8(10m7 + 8m5 + 3m3)
Simplify.
21)
1 (12x - 8)
4
A) 48x - 32
21)
B) x
C) 3x - 2
Appendix C - 4
D) 3x - 8
Use the slope-intercept form to graph the equation.
1
22) y = - x + 3
3
22)
A)
B)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
-5
-5
-10
-10
C)
5
10 x
5
10 x
D)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
-5
-5
-10
-10
Factor the trinomial completely. If the polynomial cannot be factored, write "prime."
23) x2 - 2x - 15
23)
A) prime
B) (x + 5)(x + 1)
C) (x - 5)(x + 3)
D) (x + 5)(x + 3)
24) x2 - 5x - 6
A) prime
B) (x + 1)(x - 6)
C) (x - 1)(x - 6)
D) (x - 1)(x + 1)
24)
Appendix C - 5
Solve the inequality. Graph the solution set and write it in interval notation.
25) 10 ≤ 2(x - 1) ≤ 14
A) [6, 8)
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15
B) (6, 8)
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15
C) [6, 8]
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15
D) (6, 8]
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15
25)
Find the product and simplify.
7x4y 4 ∙ y 4
26)
-56xy 8
A)
x3
-8
Solve the absolute value equation.
27) |5x + 8| + 12 = 8
4
12
A) - , 5
5
26)
B)
x4
-8
C)
x3y
-8
D)
x4
-8y
27)
4 12
B) ,
5 5
1
3
C) - , 2
2
Appendix C - 6
D) ∅
The figure shows two parallel lines intersected by a transversal. One of the angle measures is given. Find the measure
of the indicated angle.
28)
28)
37°
Find the measure of ∠2.
A) 53°
B) 27°
C) 127°
D) 37°
Graph the solution of the system of linear inequalities.
x ≥ 2y
29)
x + 2y ≤ 5
A)
29)
B)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
-5
-5
-10
-10
C)
5
10 x
5
10 x
D)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
-5
-5
-10
-10
Appendix C - 7
Graph the function.
30) g(x) = |x - 5|
30)
A)
B)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
-5
-5
-10
-10
C)
5
10 x
5
10 x
D)
y
-10
y
10
10
5
5
-5
5
10 x
-10
-5
-5
-5
-10
-10
Appendix C - 8