1. science
2. mathematics
3. statistics

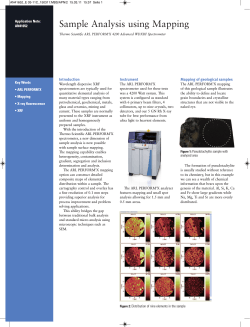
Accurate ARL Calculation for EWMA
Control Charts Monitoring
Simultaneously Normal Mean and
Variance
Sven Knoth
Advanced Mask Technology Center, Dresden, Germany
Abstract: EWMA control charts designed for monitoring the variance or the
mean and the variance of a normally distributed variable are either based on the log
transformation of the sample variance S 2 or provide only rough ARL results. Gan
(1995), as the most prominent example for the simultaneous case, calculated ARL
¯ S 2 EWMA schemes. The results in Knoth and Schmid
values precisely for X-ln
2
¯
(2002) for X-S
ones are less accurate than the former one. The reason behind
the lacking precision is that the methods usually applied for ARL calculation are
not able to handle the restricted support of the chart statistic (S 2 and, of course,
S and the range R are non-negative random variables). While in Knoth (2005)
this problem is treated for single variance monitoring by solving integral equations
with collocation methods, this paper employs collocation and ideas similar to Gan
¯ 2 EWMA control charts.
(1995) in order to obtain accurate ARL values of X-S
Additionally, the appropriate choice of the non-symmetric control limits for the S 2
part of the scheme is addressed.
Keywords: Average Run Length; Collocation; Computational methods;
Control chart design; Exponentially Weighted Moving Average.
Subject Classifications: 62L10; 60J22; 47N30; 65M70.
Address correspondence to S. Knoth, AMTC Dresden, Postfach 110161, D-01330
Dresden, Germany; Fax: +49-351-4048 9158; E-mail: [email protected]
1
1. INTRODUCTION
Control charts – core tools of Statistical Process Control (SPC) – are used
to monitor certain parameters of one or more (random) variables over time.
The main parameter of interest is the mean of the considered variable. Additionally, the performance of the variance plays a crucial role when applying a
control chart. For instance, the setting of control limits is based on reliable,
preliminary estimates of the variance. Thus, if the variance changes during
monitoring, then the average time until an alarm, false or right, is affected.
The most unpleasant case occurs when the mean changes and the variance
decreases at the same time. Then, usually, more time is needed to detect
the mean change than initially expected. Additionally, a changed (mostly
increased) variance is of importance of its own. To sum up, simultaneous
monitoring of mean and variance seems to be a quite reasonable task. Eventually, SPC software packages tend to favor most frequently X-MR (MR –
¯
¯
¯ control
Moving Range), X-R,
or X-S
control charts over single X or X
charts.
In practice, many control charts are applied at the same time. In general,
their joint behavior is not regarded; this is true even for charts which are
designed for the same unit. For example, in the previously mentioned simple
Shewhart control charts the control limits are seldom corrected to ensure a
certain behavior of the simultaneous charting scheme. It is quite simple
to obtain the same performance measures for the combined schemes as for
the single ones, if we consider only Shewhart charts. If we are interested
in applying more complex control charts such as EWMA (Exponentially
Weighted Moving Average) or CUSUM (Cumulative Sum), then we have to
face more complex problems.
There are several ways to form EWMA control charts with the objective
of monitoring mean and variance at the same time. Recall the so-called
omnibus charts in Domangue and Patch (1991) that exploit only a single
characteristic. Gan (1995) wrote a paper which plays an important rule
in the area of simultaneous EWMA charts. He demonstrated that EWMA
¯ and ln S 2 , that is, the natural logarithm of the sample
schemes based on X
variance, perform quite well and dominate the preceding omnibus charts.
Additionally, he equipped the SPC public with a numerical tool to determine the Average Run Length (ARL) of combined EWMA (and CUSUM as
well) schemes. The ARL – the average number of subgroups or individual
observations counted from monitoring startup, where it is assumed that the
change in the mean and/or variance happens only at the beginning – is the
most popular performance measure for control charts. Thus, there is high
2
interest in methods to compute this value in a quick and accurate manner.
Unfortunately, Gan’s original approach works only for ln S 2 . The same
could be observed in papers about ARL computation for single variance
control charts (see Knoth (2005) for more details). In Knoth and Schmid
¯ 2 EWMA scheme was analyzed, but with less ac(2002) the combined X-S
curacy than Gan (1995) provided. Apart from some practical reasons (ln S 2
looks more “normal” than S 2 , the scale change is transformed to a step
change, and the variance of ln S 2 does not depend on the actual value σ 2 )
one major reason drives the usage of ln S 2 – the numerical difficulties with
S 2 . These difficulties vanish after the log transformation. For ln S 2 , the
transition kernel of the EWMA sequence, more or less the distribution of
the chart statistic, is smooth, while the original sample variance leads to
a kernel which exhibits a non-smooth point. The latter is problematic for
the well-known Brook and Evans (1972) approach (Markov chain approximation) and for the so-called integral equation approach as well.
See Reynolds and Stoumbos (2001a,b, 2004) for a discussion of these
nasty problems. However, they do not provide any suitable calculation
method – their results rely mainly on Monte Carlo studies. Refer to Knoth
(2005) for a more comprehensive study of ARL calculation methods. Thereby,
mean as well as variance EWMA control charts are considered.
Hence, there are two obstacles in the way of calculation of the ARL of
combined EWMA control charts for monitoring mean and variance based
on S 2 (or S), (i) the difficulties that stem from the coupling of single charts
which was suitably solved by Gan (1995), (ii) the subtle character of the S 2
related transition kernel which was treated in Knoth (2005). The objective of
this paper is to combine ideas of both papers for getting a feasible calculation
¯ 2 EWMA control charts.
method of the joint ARL of X-S
¯ 2 EWMA CONTROL CHARTS
2. X-S
Let {Xij } be a sequence of subgroups (samples, batches) of independent
and normally distributed data. Each subgroup i consists of n observations
Xi1 , . . . , Xin . The subgroup size n can be equal to 1 if we utilize not the
usual sample variance S 2 but a variance estimator that employs the actual
mean (Reynolds and Stoumbos 2004, who preferred this version). In this
paper, which focuses more on calculation methods than on applicational
issues, this differentiation is not that important because of the equivalence
(in the in-control case, otherwise the non-central χ2 -distribution prevents
that) of both approaches in terms of the ARL calculation, if the degrees
3
of freedom in the variance part is re-adjusted. In the sequel we restrict
ourselves to the usual sample variance S 2 .
The parameters of the normal distribution are the mean µ and the variance σ 2 . Usually, we are interested in detecting changes in both directions of
µ and increases of σ 2 . Additionally, we consider here schemes which provide
signals in case of decreased variance so that we might be aware of missing
signals in the mean chart. For the topic of misleading signals we refer to
Morais and Pacheco (2006). To sum up, we consider joint schemes which
combine two-sided mean control charts with one-sided upper and two-sided
variance control charts, respectively.
To begin with, let us collect some suitable notation. The parameter
values, which describe the stable performance of the monitored process, are
µ0 and σ02 . As long as the stable and the actual parameter values coincide we
call the process “in-control”: it is otherwise “out-of-control” (unfortunately,
we have to base our decision on data and not on exact knowledge of µ and σ).
¯ 2 EWMA control charts are based on the two EWMA sequences
Then, X-S
µ
{Zi } and {Ziσ }, that is,
n
n
X
¯i = 1
X
Xij
n
Si2
z0µ
Z0σ
Ziσ
j=1
Z0µ
Ziµ
=
= (1 −
µ
λµ )Zi−1
1 X
¯i 2 ,
=
Xij − X
n−1
j=1
¯i
+ λµ X
=
z0σ
,
σ
= (1 − λσ )Zi−1
+ λσ Si2 .
The design parameters λµ and λσ are chosen from the interval (0, 1] to ensure
a certain signaling behavior, where small values increase the detection power
for small changes and vice versa. The starting values z0µ and z0σ are usually
set to µ0 and σ02 , respectively. Then, as long the process is in control, the
expectations of both EWMA sequences are equal to their target values.
An alarm is given at time point L if at least one of the single charts
signals,
L = min{Lµ , Lσ } ,
(
s
)
λµ σ0
√
Lµ = min i ∈ N :
− µ0 | >
:= cµ
,
2 − λµ n
(
)
r
r
λ
2
σ
Lσ = min i ∈ N : Ziσ − σ02 > c∗σ := cσ
σ2 .
2 − λσ n − 1 0
|Ziµ
c∗µ
As usual, the alarm thresholds on the righthand sides of Lµ and Lσ are
normalized with the asymptotic standard deviation of the chart statistics Ziµ
4
and Ziσ , respectively. The values cµ and cσ are called critical values. In the
sequel, however, we utilize the starred versions. For the two-sided variance
case we have to introduce a further limit because of the non-symmetric
behavior of Si2 and consequently Ziσ (see Section 4).
The previously mentioned ARL could be described as the expectation of
L. To be precise, for fixed values of the so-called head starts z0µ and z0σ , and
for given actual values of µ and σ, which are assumed to be valid for the
whole averaging process, denote
E(L) = E(L|µ, σ, z0µ , z0σ ) .
Of course, as in the univariate case the Markov chain as well the integral
equation approach could be established for the full 2-dimensional model.
Both end in large dimensions of the resulting linear equation system if a
reasonable precision is needed. See Knoth and Schmid (2002) for some results in that direction, where it had to be used for autocorrelated data. That
approach becomes even more complex if one tries to employ the collocation
ideas given in Knoth (2005).
3. ARL CALCULATION
Ideas like in Gan (1995) that are based on Waldmann (1986) should be
exploited in order to get a more feasible approach than the full 2-dimensional
one. First, the parameters µ0 and σ02 are set to 0 and 1, respectively, for
the sake of simplicity. Denote P (·) the probability measure of our series for
a fixed parameter set of µ, σ, z0µ , z0σ . Then for any j ∈ N regarding the
¯ and S 2
independence of X
P (L > j) = P (Lµ > j) P (Lσ > j) .
Using the well-known relation
E(L) =
∞
X
P (L > j)
j=0
and the geometric tail behavior of the distribution of L (see Waldmann
(1986), Gan (1995), Knoth (1998), and Madsen and Conn (1973) – the essential assumption for the asymptotic geometric tail is some quasi-positiveness
of the kernel of the joint scheme, which is mostly fulfilled for the considered
control charts) allows us to establish the following ARL bounds:
ARL±
J =
J−1
X
j=0
P (L > j) +
P (L > J)
.
1 − m±
J
5
The choice of the truncation point J relies on the distance between the
bounds ARL±
J and could be rather small for small distances already. The
constants m±
J are defined as in Waldmann (1986) and Gan (1995), that
is, they stand for sup and inf of P (L > j; z0µ , z0σ )/P (L > j − 1; z0µ , z0σ )
over the permissible domains of starting values z0µ and z0σ . These values m±
J
converge rapidly to a common limit which resembles the eigenvalue of largest
magnitude of the joint transition kernel. Waldmann (1986), and later Gan
(1995), utilized quadrature rules in order to calculate numerically the values
P (L > j) for j = 1, 2, . . . , J by means of the following iteration rule for the
single control charts:
∗
P (Lµ > 1)(z0µ ) =
Zcµ
f (z0µ , z) dz ,
−c∗µ
∗
P (Lµ > j)(z0µ ) =
Zcµ
P (Lµ > j − 1)(z) fµ (z0µ , z) dz .
−c∗µ
Thereby, f (·) denotes the corresponding transition kernel, which is equal to
z − (1 − λµ ) z0µ
1
µ
fµ (z0 , z) =
φµ,σ
λµ
λµ
for the mean chart. φ(·) denotes the probability density function (pdf) of
a normally distributed variable with mean µ and variance σ 2 . For the S 2
chart we have to use (and, of course, different limits in the integral)
1 2 n − 1 z − (1 − λσ ) z0σ
n−1
σ
fσ (z0 , z) =
χ
.
2
λσ
σ
λσ
σ2
χ2 (·) denotes the pdf of a chi-squared distributed random variable with
n − 1 degrees of freedom. Gan (1995) considered ln S 2 and obtained a
different version of the variance chart transition kernel. Thus, he was able
to approximate the integrals in both iteration sequences P (Lµ > j) and
P (Lσ > j) with Gauss-Legendre quadratures with small absciccae numbers
to ensure reasonable precision. Unfortunately, if we are interested in S 2
instead of ln S 2 , the same problem arises as for the single variance chart.
In Knoth and Schmid (2002) both iteration sequences were approximated
by terms, which come from the Markov chain approach. Instead of applying the truncation at a certain J the whole problem is transformed into a
6
Sylvester matrix equation system that is solved by employing a numerical
library. Unfortunately, it inherits the precision losses from the S 2 part and,
consequently, large matrix dimensions are needed to get higher accuracy.
A small study should demonstrate the ability of different approaches to
¯ 2 EWMA control charts. Let
deal with the subtle ARL calculation for X-S
us consider:
1. Pure transfer of Gan (1995), who utilized Gauss-Legendre quadrature
(GL) for calculating the iteration sequences P (Lµ > j) and P (Lσ > j),
j = 1, 2, . . .
2. Apply the Simpson (S) rule instead of GL for the S 2 part.
3. Apply the midpoint rule instead of GL, which is equivalent to the
popular Markov chain approximation (M 1) – Morais and Pacheco
¯ S 2 EWMA charts (for both the mean and
(2000) utilized this for X-ln
the variance chart).
4. Collocation (C) similar to Knoth (2005), described in more detail in
the Appendix of this paper.
5. Like in Knoth and Schmid (2002), employ Markov chain approximation (M 2) for both charts and solve a Sylvester matrix equation.
Note that with one exception (Sylvester matrix equation) all approaches
¯ part. The subgroup size
use always Gauss-Legendre quadratures for the X
n is equal to 5 like in Gan (1995). The smoothing parameters are taken as
λµ = 0.134 from Gan (1995) and λσ = 0.1 that is more a first shot than
a result of some optimization. However, it helps to build a control chart
which beats Gan’s best combination as will be demonstrated in Section
4. Then c∗µ = 0.345 477 and c∗σ = 0.477 977 are used, which yields an incontrol ARL of 252.3 of the combined scheme and equal ARLs of the single
charts. A Monte Carlo study with 109 replicates validates the above joint
ARL value by resulting in 252.307 with standard error 0.0078. In Figure 1
the approximated ARL versus matrix dimension N (each method relies on
matrices) are plotted. Note that the truncation point J that is needed for
approaches 1 to 4 is always chosen in the same way. The distance between
the bounds mentioned in the beginning of the section, ARL±
J , should be
smaller than 10−8 . The matrix dimension N is only related to the quality
of the survival function approximation.
7
Figure 1. Precision of different ARL computation methods for the in¯ 2 EWMA control chart monitoring the mean (2-sided)
control ARL of a X-S
and variance (upper) of normally distributed data, the true value is 252.3
and the smoothing values are λµ = 0.134 and λσ = 0.1; S – Simpson rule,
M 1 – Markov chain (midpoint rule), M 2 – Markov chain (Sylvester matrix
equation), C – Collocation.
The Gauss-Legendre quadrature based results are not drawn in Figure 1,
because they oscillate more than all the others (see Table 1 for some numerical results). At first sight of Figure 1, the collocation method exhibits the
best performance. For dimension N = 23, collocation already ensures the
first 6 digits after the decimal point. No other method in the study attains
this accuracy with N below 300. Even if we regard the higher complexity
of the collocation approach, which leads to the highest computing times for
fixed N among the candidates, collocation is the clear favorite. See Table 1
for the corresponding computing times. The second and third best ones are
the two Markov chain approaches, followed by Simpson and Gauss-Legendre
quadrature based ones.
Table 1. Resulting ARL approximations and CPU times (measured in
hundredth seconds on an Athlon XP 1.4 GHz) for selected matrix dimensions
N and all methods under consideration; the true value is 252.2999.
Method
Gauss-Leg.
Simpson
M. chain 1
M. chain 2
Collocation
13
25
60.8717
1
5.2588
1
232.4026
<1
211.3234
<1
253.3603
2
90.9297
1
-1
1
245.2234
<1
239.9381
1
252.2999
8
matrix dimension N
51
101
143.4348
2
297.8329
2
250.5108
2
249.3160
5
252.2999
35
253.1860
5
249.0502
5
252.2235
5
251.9535
32
252.2999
140
201
301
252.1741
30
252.5606
30
252.3001
31
252.2515
286
252.2999
583
252.6392
65
252.3129
65
252.2729
68
252.2598
1221
252.2999
1323
Thus, if we are interested in getting a quick and nearly accurate result,
8
then we would take the Markov chain approximation M 1. If we prefer high
accuracy, then collocation is the first choice.
The numbers in Table 2 demonstrate how the collocation approach works
for smaller λσ down to 0.001 and less subgroup sizes n. The parameter λµ
remains unchanged because it is numerically less subtle. Table 2 gives the
matrix dimensions Nσ (only the resolution of the S 2 related approximation,
just Nσ , is increased; Nµ is fixed at 51) and the resulting final thresholds,
that is, c∗µ and c∗σ . Fortunately, the matrix dimension Nσ does not increase
Table 2. Resolution (matrix dimension) Nσ needed to ensure 6 digits accuracy for the in-control ARL (252.3). Additionally, both (finalized) critical
values c∗µ and c∗σ (second and third entry) are given.
n
5
4
3
2
0.1
0.05
λσ
0.01
23
0.345477
0.477977
23
0.386268
0.563641
17
0.446048
0.713918
23
0.546349
1.081116
31
0.345381
0.284547
31
0.386166
0.332911
21
0.445939
0.416409
31
0.546243
0.614829
60
0.345962
0.075633
62
0.386822
0.087563
37
0.446709
0.107662
61
0.547224
0.153289
0.005
0.001
83
0.347443
0.038398
85
0.388478
0.044359
50
0.448622
0.054313
83
0.549569
0.076655
167
0.356187
0.006213
174
0.398254
0.007149
107
0.459910
0.008701
176
0.563392
0.012100
too fast. Note that small λ’s such as 0.001 are not reasonable at all. Knoth
(2006) provides a small study for one-sided S 2 EWMA charts that illustrates
it. While the ARL for detecting a given scale change decreases, the in-control
probability of an early alarm (right at the first observation) increases heavily.
In Section 6 the collocation approach is described in more detail. In
the next Section we employ this ARL calculation method to compare Gan’s
(ln S 2 based) ARL results with the ARL values of the competing S 2 based
simultaneous EWMA chart.
9
¯ S 2 AND X-S
¯ 2 EWMA CHARTS
4. COMPARE X-ln
Gan (1995) compared omnibus charts described in Domangue and Patch
(1991) with two joint EWMA charts and one CUSUM combination in terms
of their ARL. Both EWMA and CUSUM are built with ln S 2 . The EWMA
charts work considerably well. Here, we want to add for both EWMA
schemes the corresponding performance of the S 2 based charts. As mentioned in the previous Section, we take the same λµ = 0.134 like Gan, but
set λσ = 0.1, which is sufficiently powerful – as we will see soon. The critical limits c∗µ and c∗σ are chosen to provide an in-control ARL 252.3 for the
¯ chart looks similar:
combined scheme. Recall that Gan’s limit for the X
c∗µ,Gan = 0.345 vs. c∗µ = 0.345477. These limits ensure also equal in-control
ARLs for the single charts, namely 499.3. Note that our comparison is not
really fair, because Gan’s EWMA sequence exhibits a lower reflection barσ
σ
+ ln Si2 }. Then, Gan calculated
= max{0, (1 − λσ )Zi−1,Gan
rier, i. e. Zi,Gan
σ
the ARL for z0,Gan = 0 that corresponds to the worst case for detecting an
increase in σ 2 (the smoothing value is λσ,Gan = 0.043).
For the S 2 based chart, we calculate the ARL as usual for EWMA charts,
that is, for z0 = σ02 = 1, which is not the lowest position of Ziσ . It is difficult
to compare these charts in an appropriate manner (we have to switch to the
steady-state ARL or we should introduce a reflection for the S 2 chart like
in the comparison in Knoth 2005). In Table 3, however, we give ARL values
of both (upper) EWMA charts.
¯ S 2 (EEU ), and of
Table 3. Subset of ARLs from Gan (1995), that is, X-ln
2
¯
X-S EWMA charts calculated by collocation.
∆
0
0.20
0.40
1.00
σ/σ0
1.00 1.05 1.25 1.00 1.05 1.25 1.00 1.05 1.25 1.00 1.05 1.25
¯ S 2 252.3 113.0 16.6 129.7 78.3 15.9 48.8 39.4 14.2 10.2 10.0 8.3
X-ln
¯ 2 252.3 101.2 13.9 129.3 72.6 13.4 48.6 38.1 12.3 10.1 9.9 7.7
X-S
√
Note that the shift ∆ is measured in σ0 / n units (subgroup size n) like
in Gan (1995). We see from Table 3 that the S 2 based version works slightly
better. Remember that the comparison suffers from the same dilemma as
many EWMA-CUSUM comparisons.
We consider now a comparison for the double two-sided schemes. It
would remain an unfair comparison if CUSUM would be one competitor.
¯ S 2 EWMA chart and our X-S
¯ 2 EWMA chart,
Gan’s double two-sided X-ln
10
however, act similarly. According to Gan, the critical limits of his twosided ln S 2 were chosen to minimize the ARL for detecting an increase to
σ = 1.25σ0 (now λσ,Gan = 0.106). His resulting critical limits are c∗µ,Gan =
0.345, c∗σ,lower,Gan = −0.867 and c∗σ,upper,Gan = 0.215. Here, we want to
¯ 2 chart, and with so-called
compare this optimal chart with a similar X-S
ARL-unbiased versions of both. The analysis of the former is based again
on collocation methods and provide c∗µ = 0.345313, c∗σ,lower = −0.383153 and
c∗σ,upper = 0.53 (the upper variance limit was fixed, the lower one and the
mean limit are chosen to give the joint ARL 252.3 and equal ARL values of
the mean and the variance chart).
The term ARL-unbiased was defined in Pignatiello et al. (1995) and
broadly applied for variance control charts in Acosta-Mej´ıa and Pignatiello
(2000). Roughly speaking, the max of the ARL for fixed µ = µ0 = 0 and for
varying σ should be attained at σ = σ0 = 1. While it is trivial for symmetric
distributions (symmetric lower and upper control limits ensure that), it is
more demanding to choose the usually non-symmetric limits to provide the
max at the right position. Here, we try to solve the following task:
1. Joint ARL is again 252.3.
2. ARLs of the single charts are equal.
3. The slope (of the ARL function) in σ direction at σ = σ0 = 1 is 0.
This is done numerically based on Gan’s methods and on collocation. The re¯ S 2 EWMA scheme are c∗
sulting critical limits of Gan’s X-ln
µ,Gan = 0.345382,
∗
∗
cσ,lower,Gan = −0.824585, and cσ,upper,Gan = 0.262703. The respective limits
¯ 2 EWMA chart are c∗ = 0.345271, c∗
of the X-S
µ
σ,lower = −0.363404, and
∗
cσ,upper = 0.582758. The variance limits are slightly increased compared to
the previous designs. Thus, both schemes now detect decreases in σ faster,
while the increase detection ability became worse. In Figure 2 we see the
√
results for µ = µ0 + ∆/ n , ∆ ∈ {0, 0.2, 0.4, 1}.
For the given domain of possible σ values, the S 2 based scheme is better
than the ln S 2 one. Only for σ values smaller than 0.7 or larger than 1.3,
and for µ = 1 and σ < 1 the ln S 2 based version provides a better ARL
performance. The latter demonstrates the advantage of the more symmetric
behavior of the ln S 2 version. The S 2 version, however, becomes faster and
faster, when the magnitude of the mean shift and the variance increase in
the same time.
11
5. CONCLUSIONS
The main result of the current paper is that we are able to get accurate ARL
¯ 2 EWMA control charts. To do this, one should use colloresults for X-S
cation for the S 2 part. Standard methods like the Markov chain approach
provide quick and nearly accurate results, but do not attain high accuracy.
Moreover, as already seen in Knoth (2005) and several papers mentioned
therein S 2 based schemes perform better than ln S 2 ones in terms of their
ARL. However, the current paper does not provide a complete study. A
further paper might fill this gap.
For truly two-sided variance EWMA charts one has to look for so-called
ARL-unbiased designs. With recent computer technology (PCs, not clusters
or bigger boxes, which are even faster), this is done with CPU times of some
seconds only.
To get rid of large delays in detecting mean changes in the presence of simultaneous variance decreases, it is enough to take a slightly non-symmetric
design (hence, the scheme becomes “ARL-biased”) as Gan (1995) already
did.
6. APPENDIX
Here, some more details of the collocation method as a plugin for calculating
the iterations of P (Lσ > j) follow. Note that for the whole calculation
process we derive equations for an approximation of the run length survival
function and not for the true function itself, that is, all terms like P (L > j)
refer now to the numerical approximation.
¯ chart the Gauss-Legendre quadrature is employed,
Recall that for the X
which is here the most powerful one. Thus, take N Gauss-Legendre roots
zs and weights ws on the integration interval [−c∗µ , c∗µ ], so that
P (Lµ > j)(zr ) =
N
X
ws P (Lµ > j − 1)(zs ) fµ (zr , zs ) , r = 1, 2, . . . , N
s=1
provides us with a numerical recipe for the iteration sequence P (Lµ > j).
Please do not confuse z0µ (or z0σ ) from Section 3, where the 0 stands for in
control, with zs . Here, s points to sth quadrature node.
In Section 3 the same was applied for P (Lσ > j) besides the Simpson
and midpoint rules as competing quadrature methods.
Now, the collocation method should be presented. Collocation means
that the solution is built as linear combination of certain base functions
12
{Ts (·)}. Thus, set for each j
P (Lσ > j)(z) =
N
X
gjs Ts (z)
s=1
via
N
X
gjs Ts (zr ) =
s=1
N
X
∗
1+c
Z σ
gj−1,s
s=1
Ts (z)fσ (zr , z) dz , r = 1, 2, . . . , N
0
on a suitably chosen grid z1 < z2 < . . . < zN and an easily derived starting
set {g1s } we obtain the wanted iteration sequence for approximating the
run length survival function. We calculate the new values {gjs } step by step
while solving the above equation systems.
If we take step functions as base, then we arrive again at the Markov
chain approach. Usual bases are monomials like 1, z, z 2 , . . . , z N −1 , Lagrange
or Chebyshev polynomials (some adaption for usage on [0, 1 + c∗σ ] is needed)
Ts (z) = cos s arccos(z) , s = 0, 1, . . . , N − 1 , z ∈ [−1, 1] ,
which ensure more stable numerical quadratures than monomials or Lagrange polynomials. It could be worthwile to compare monomials and
Chebyshev polynomials in terms of the resulting ARL computing time. For
monomials it could be easier to establish faster iterations.
¯ and for S 2 we are able to approximate the survival function
Now, for X
µ/σ
P (Lµ/σ > j) for arbitrary z and not only at the nodes zr . Recall that the
grids used for the single charts differ from each other. Thus, zs stands for
the respective grid. In terms of vector arithmetics the methods look like:
P~j = MP~j−1 ,
µ 0
) ,
P~j = P (Lµ > j)(z1µ ), . . . , P (Lµ > j)(zN
M = Mrs , Mrs = ws fµ (zr , zs ) ,
for the simple mean part and
N ~gj = O~gj−1 ,
~gj = gj1 , . . . , gjN ,
N = Nrs , Nrs = Ts (zrσ ) ,
∗
1+c
Z σ
O = Ors , Ors =
Ts (z σ )fσ (zrσ , z σ ) dz σ
0
13
for the more subtle S 2 chart. Here, we recognize the source of the higher
computing times for fixed N compared to the competing methods. Fortunately, the matrices N and O do not depend on j so that the solution of
the linear equation system for each j could be accelerated. The entries of O
are calculated numerically, where only small numbers of quadrature points
are needed (do not confuse these quadratures with the upper ones) for high
accuracy. Note that for this paper Chebyshev polynomials are used (just in
case when for very small λ large values of N could be necessary). For the
monomials base perhaps, faster solution is possible.
For the two-sided variance chart the collocation approach becomes even
more difficult to describe. Instead of bases which contain smooth, nonconstant functions over the whole interval [1 + c∗σ,lower , 1 + c∗σ,upper ], we use
now piecewise defined functions, which vanish outside a small supporting
interval. For details about this we refer to Knoth (2005). The reason behind
this detour is that the piecewise approach is considerably more precise than
the full approach and does not need more computing time for the same N .
Eventually, the numerical approach for the ARL-unbiased design will be
sketched. As mentioned in Section 4, three conditions have to be fulfilled
and three critical values are unknown. The iteration starts with the upper scheme that yields the target joint in-control ARL and equal ARLs of
the single charts. Then, a slightly increased upper variance limit is fixed.
The remaining limits are calculated to ensure the previous mentioned ARL
design. Finally, by means of the secant rule this upper variance limit is
changed as long as (Lµ0 ,σ0 −ε − Lµ0 ,σ0 +ε )/(2ε) (this secant should mimic the
slope at (µ0 , σ0 ) in σ-direction) is larger than 10−6 . Thereby, ε is set to 10−4 .
After updating the upper variance limit, the lower one and the mean limit
are again derived to provide the target joint ARL and equal ARL values
of the separate charts. Figure 2 demonstrates that the iteration provides
reasonable results.
References
Acosta-Mej´ıa, C. A. and Pignatiello, J. J., Jr. (2000). Monitoring Process
Dispersion Dithout Subgrouping, Journal of Quality Technology 32: 89–
102.
Brook, D. and Evans, D. A. (1972). An Approach to the Probability Distribution of CUSUM Run Length, Biometrika 59: 539–549.
14
Domangue, R. and Patch, S. (1991). Some Omnibus Exponentially Weighted
Moving Average Statistical Process Monitoring Schemes, Technometrics 33: 299–313.
Gan, F. F. (1995). Joint Monitoring of Process Mean and Variance Using
Exponentially Weighted Moving Average Control Charts, Technometrics 37: 446–453.
Knoth, S. (1998). Exact Average Run Lengths of CUSUM Schemes for
Erlang Distributions, Sequential Analysis 17: 173–184.
Knoth, S. (2005). Accurate ARL Computation for EWMA-S 2 Control
Charts, Statistics and Computing 15: 341–352.
Knoth, S. (2006). The Art of Evaluating Monitoring Schemes – How to
Measure the Performance of Control Charts?, in Frontiers in Statistical Quality Control 8, H.-J. Lenz and P.-T. Wilrich, eds., pp. 74-99,
Heidelberg: Springer.
Knoth, S. and Schmid, W. (2002). Monitoring the Mean and the Variance
of a Stationary Process, Statistica Neerlandica 56: 77–100.
Madsen, R. W. and Conn, P. S. (1973). Ergodic Behavior for Nonnegative
Kernels, Annals of Probability 1: 995–1013.
Morais, M. C. and Pacheco, A. (2000). On the Performance of Combined
EWMA Schemes for µ and σ: A Markovian Approach, Communications
in Statistics - Simulation & Computation 29: 153–174.
Morais, M. C. and Pacheco, A. (2006). Misleading Signals in Joint Schemes
for µ and σ, in Frontiers in Statistical Quality Control 8, H.-J. Lenz
and P.-T. Wilrich, eds., pp. 100-123, Heidelberg: Springer.
Pignatiello, J. J., Jr., Acosta-Mej´ıa, C. A., and Rao, B. V. (1995). The
Performance of Control Charts for Monitoring Process Dispersion, 4th
Industrial Engineering Research Conference, pp. 320–328.
Reynolds, M. R., Jr. and Stoumbos, Z. G. (2001a). Individuals Control
Schemes for Monitoring the Mean and Variance of Processes Subject
to Drifts, Stochastic Analysis and Applications 19: 863–892.
Reynolds, M. R., Jr. and Stoumbos, Z. G. (2001b). Monitoring the Process Mean and Variance Using Individual Observations and Variable
Sampling Intervals, Journal of Quality Technology 33: 181–205.
15
Reynolds, M. R., Jr. and Stoumbos, Z. G. (2004). Control Charts and the
Efficient Allocation of Sampling Resources, Technometrics 46: 200–214.
Waldmann, K.-H. (1986). Bounds for the Distribution of the Run Length of
Geometric Moving Average Charts, Journal of Royal Statistical Society,
Series C 35: 151–158.
16
Figure 2. ARL function of double two-sided EWMA charts (Gan’s EE
¯ 2 -EWMA), mean is fixed at µ = µ0 + ∆/√n , ∆ ∈ {0, 0.2, 0.4, 1},
and X-S
in-control ARL 252.3.
17