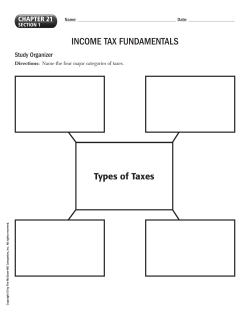
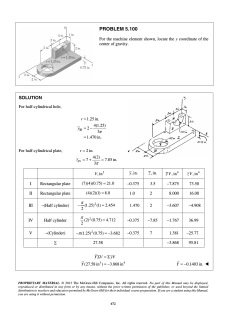
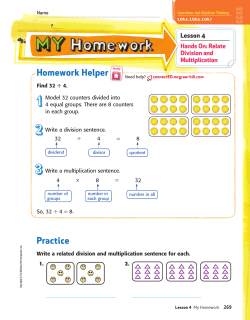
PROBLEM 6.77
Determine the components of all forces acting on member ABCD of the
assembly shown.
SOLUTION
Free body: Entire assembly:
ΣM B = 0: D (120 mm) − (480 N)(80 mm) = 0
D = 320 N
ΣFx = 0: Bx + 480 N = 0
B x = 480 N
ΣFy = 0: By + 320 N = 0
B y = 320 N
Free body: Member ABCD:
ΣM A = 0: (320 N)(200 mm) − C (160 mm) − (320 N)(80 mm)
− (480 N)(40 mm) = 0
C = 120.0 N
ΣFx = 0: Ax − 480 N = 0
A x = 480 N
ΣFy = 0: Ay − 320 N − 120 N + 320 N = 0
A y = 120.0 N
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
858
PROBLEM 6.79
For the frame and loading shown, determine the components of all
forces acting on member ABC.
SOLUTION
Free body: Entire frame:
ΣM E = 0: − Ax (4) − (20 kips)(5) = 0
Ax = −25 kips,
A x = 25.0 kips
ΣFy = 0: Ay − 20 kips = 0
Ay = 20 kips
A y = 20.0 kips
Free body: Member ABC:
Note: BE is a two-force member, thus B is directed along line BE and By =
2
Bx .
5
ΣM C = 0: (25 kips)(4 ft) − (20 kips)(10 ft) + Bx (2 ft) + By (5 ft) = 0
−100 kip ⋅ ft + Bx (2 ft) +
2
Bx (5 ft) = 0
5
Bx = 25 kips
By =
B x = 25.0 kips
2
2
( Bx ) = (25) = 10 kips
5
5
B y = 10.00 kips
ΣFx = 0: C x − 25 kips − 25 kips = 0
C x = 50 kips
C x = 50.0 kips
ΣFy = 0: C y + 20 kips − 10 kips = 0
C y = −10 kips
C y = 10.00 kips
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
860
PROBLEM 6.83
Determine the components of the reactions at A and E if a 750-N force
directed vertically downward is applied (a) at B, (b) at D.
SOLUTION
Free body: Entire frame:
The following analysis is valid for both parts (a) and (b) since position of load on its line of action is immaterial.
ΣM E = 0: − (750 N)(80 mm) − Ax (200 mm) = 0
Ax = − 300 N
A x = 300 N
ΣFx = 0: E x − 300 N = 0 E x = 300 N E x = 300 N
ΣFy = 0: Ay + E y − 750 N = 0
(a)
(1)
Load applied at B.
Free body: Member CE:
CE is a two-force member. Thus, the reaction at E must be directed along CE.
Ey
300 N
From Eq. (1):
=
75 mm
250 mm
E y = 90 N
Ay + 90 N − 750 N = 0
Ay = 660 N
Thus, reactions are
(b)
A x = 300 N
,
A y = 660 N
E x = 300 N
,
E y = 90.0 N
Load applied at D.
Free body: Member AC:
AC is a two-force member. Thus, the reaction at A must be directed along AC.
Ay
300 N
=
125 mm
250 mm
Ay = 150 N
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
864
PROBLEM 6.83 (Continued)
Ay + E y − 750 N = 0
From Eq. (1):
150 N + E y − 750 N = 0
E y = 600 N E y = 600 N
Thus, reactions are
A x = 300 N
,
A y = 150.0 N
E x = 300 N
,
E y = 600 N
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
865