Download Report

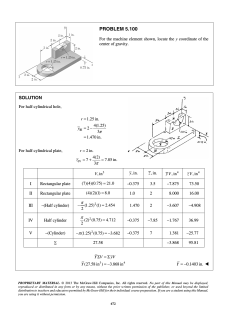
PROBLEM 4.93
A 4 × 8-ft sheet of plywood weighing 40 lb has been temporarily
propped against column CD. It rests at A and B on small wooden
blocks and against protruding nails. Neglecting friction at all
surfaces of contact, determine the reactions at A, B, and C.
SOLUTION
Free-Body Diagram:
We have five unknowns and six equations of equilibrium. Plywood sheet is free to move in x direction, but
equilibrium is maintained (ΣFx = 0).
ΣM A = 0: rB /A × ( B y j + Bz k ) + rC /A × C k + rG /A × ( −40 lb) j = 0
i j
5 0
0 By
k
i
j
k
i
j
k
0 + 4 4sin 60° −4cos 60° + 2 2sin 60° −2 cos 60° = 0
Bz 0
C
−40
0
0
0
(4C sin 60° − 80 cos 60°) i + (−5Bz − 4C ) j + (5B y − 80)k = 0
Equating the coefficients of the unit vectors to zero,
i:
4C sin 60° − 80 cos 60° = 0
j:
−5Bz − 4C = 0
k:
5B y − 80 = 0
ΣFy = 0:
Ay + B y − 40 = 0
ΣFz = 0:
Az + Bz + C = 0
C = 11.5470 lb
Bz = 9.2376 lb
B y = 16.0000 lb
Ay = 40 − 16.0000 = 24.000 lb
Az = 9.2376 − 11.5470 = −2.3094 lb
A = (24.0 lb)j − (2.31 lb)k ; B = (16.00 lb) j − (9.24 lb)k ; C = (11.55 lb)k
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
450
PROBLEM 4.99
The 45-lb square plate shown is supported by three vertical wires.
Determine the tension in each wire.
SOLUTION
Free-Body Diagram:
ΣM B = 0: rC /B × TC j + rA/B × TA j + rG /B × (−45 lb) j = 0
[−(20 in.)i + (15 in.)k ] × TC j + (20 in.)k × TA j
+ [−(10 in.)i + (10 in.)k ] × [−(45 lb)j] = 0
−20TC k − 15TC i − 20TAi + 450k + 450i = 0
Equating to zero the coefficients of the unit vectors,
k:
−20TC + 450 = 0
TC = 22.5 lb
i:
−15(22.5) − 20TA + 450 = 0
TA = 5.625 lb
ΣFy = 0:
TA + TB + TC − 45 lb = 0
5.625 lb + TB + 22.5 lb − 45 lb = 0
TB = 16.875 lb
TA = 5.63 lb; TB = 16.88 lb; TC = 22.5 lb
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
458
PROBLEM 4.105
A 2.4-m boom is held by a ball-and-socket joint at C and by two
cables AD and AE. Determine the tension in each cable and the
reaction at C.
SOLUTION
Free-Body Diagram:
(ΣMAC = 0).
Five unknowns and six equations of equilibrium, but equilibrium is maintained
rB = 1.2k
rA = 2.4k
AD = −0.8i + 0.6 j − 2.4k
AD = 2.6 m
AE = 0.8i + 1.2 j − 2.4k
AE = 2.8 m
AD TAD
=
(−0.8i + 0.6 j − 2.4k )
AD 2.6
AE TAE
=
=
(0.8i + 1.2 j − 2.4k )
AE 2.8
TAD =
TAE
ΣM C = 0: rA × TAD + rA × TAE + rB × (−3 kN) j = 0
i
j
k
i
j
k
TAD
T
0
0
2.4
0
2.4 AE + 1.2k × (−3.6 kN) j = 0
+ 0
2.6
2.8
0.8 1.2 −2.4
−0.8 0.6 −2.4
Equate coefficients of unit vectors to zero:
i : − 0.55385TAD − 1.02857TAE + 4.32 = 0
(1)
j : − 0.73846TAD + 0.68671TAE = 0
TAD = 0.92857TAE
From Eq. (1):
(2)
−0.55385(0.92857)TAE − 1.02857TAE + 4.32 = 0
1.54286TAE = 4.32
TAE = 2.800 kN
TAE = 2.80 kN
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
465
PROBLEM 4.105 (Continued)
From Eq. (2):
TAD = 0.92857(2.80) = 2.600 kN
TAD = 2.60 kN
0.8
0.8
(2.6 kN) +
(2.8 kN) = 0
2.6
2.8
0.6
1.2
(2.6 kN) +
(2.8 kN) − (3.6 kN) = 0
ΣFy = 0: C y +
2.6
2.8
2.4
2.4
(2.6 kN) −
(2.8 kN) = 0
ΣFz = 0: C z −
2.6
2.8
ΣFx = 0: C x −
Cx = 0
C y = 1.800 kN
C z = 4.80 kN
C = (1.800 kN) j + (4.80 kN)k
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
466
PROBLEM 4.113
A 100-kg uniform rectangular plate is supported in the position
shown by hinges A and B and by cable DCE that passes over a
frictionless hook at C. Assuming that the tension is the same in
both parts of the cable, determine (a) the tension in the cable,
(b) the reactions at A and B. Assume that the hinge at B does
not exert any axial thrust.
SOLUTION
rB/A (960 − 180)i = 780i
Dimensions in mm
960
450
− 90 i +
k
2
2
= 390i + 225k
= 600i + 450k
rG/A =
rC/A
T = Tension in cable DCE
CD = −690i + 675 j − 450k
CD = 1065 mm
CE = 270i + 675 j − 450k
CE = 855 mm
T
(−690i + 675 j − 450k )
1065
T
TCE =
(270i + 675 j − 450k )
855
W = −mgi = −(100 kg)(9.81 m/s 2 ) j = −(981 N) j
TCD =
ΣM A = 0: rC/A × TCD + rC/A × TCE + rG/A × (−Wj) + rB/A × B = 0
i
j
k
i
j
k
T
T
600
0
450
450
+ 600 0
1065
855
270 675 −450
−690 675 −450
i
+ 390
0
j
0
−981
k
i
225 + 780
0
0
j
0
k
0 =0
By
Bz
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
481
PROBLEM 4.113 (Continued)
Coefficient of i:
−(450)(675)
T
T
− (450)(675)
+ 220.73 × 103 = 0
1065
855
T = 344.64 N
Coefficient of j:
(−690 × 450 + 600 × 450)
T = 345 N
344.64
344.64
+ (270 × 450 + 600 × 450)
− 780 Bz = 0
1065
855
Bz = 185.516 N
Coefficient of k: (600)(675)
344.64
344.64
+ (600)(675)
− 382.59 × 103 + 780 By = 0 By = 113.178 N
1065
855
B = (113.2 N) j + (185.5 N)k
ΣF = 0: A + B + TCD + TCE + W = 0
690
270
(344.64) +
(344.64) = 0
1065
855
Coefficient of i:
Ax −
Ax = 114.5 N
Coefficient of j:
Ay + 113.178 +
675
675
(344.64) +
(344.64) − 981 = 0
1065
855
Ay = 377 N
Coefficient of k:
Az + 185.516 −
450
450
(344.64) −
(344.64) = 0
1065
855
Az = 141.5 N
A = (114.5 N)i + (377 N) j + (144.5 N)k
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
482
PROBLEM 4.138
The frame ACD is supported by ball-and-socket joints at A
and D and by a cable that passes through a ring at B and is
attached to hooks at G and H. Knowing that the frame
supports at Point C a load of magnitude P = 268 N, determine
the tension in the cable.
SOLUTION
Free-Body Diagram:
AD (1 m)i − (0.75 m)k
=
AD
1.25 m
= 0.8i − 0.6k
λ AD =
λ AD
TBG = TBG
= TBG
TBH = TBH
= TBH
BG
BG
−0.5i + 0.925 j − 0.4k
1.125
BH
BH
0.375i + 0.75 j − 0.75k
1.125
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
522
PROBLEM 4.138 (Continued)
rB /A = (0.5 m)i; rC/A = (1 m)i; P = −(268 N)j
To eliminate the reactions at A and D, we shall write
ΣM AD = 0:
λ AD ⋅ (rB /A × TBG ) + λ AD ⋅ (rB /A × TBH ) + λ AD ⋅ (rC /A × P) = 0
(1)
Substituting for terms in Eq. (1) and using determinants,
−0.6
−0.6
−0.6
0.8
0
0.8
0
0.8
0
TBG
TBH
+ 0.5
+ 1
0.5
0
0
0
0
0
0 =0
1.125
1.125
−0.5 0.925 −0.4
0.375 0.75 −0.75
0 −268
0
Multiplying all terms by (–1.125),
0.27750TBG + 0.22500TBH = 180.900
For this problem,
(2)
TBG = TBH = T
(0.27750 + 0.22500)T = 180.900
T = 360 N
PROPRIETARY MATERIAL. © 2013 The McGraw-Hill Companies, Inc. All rights reserved. No part of this Manual may be displayed,
reproduced or distributed in any form or by any means, without the prior written permission of the publisher, or used beyond the limited
distribution to teachers and educators permitted by McGraw-Hill for their individual course preparation. If you are a student using this Manual,
you are using it without permission.
523