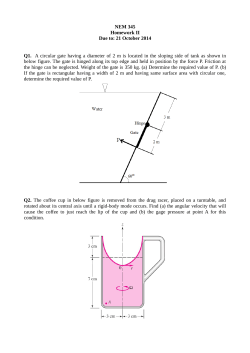
Tunable diameter electrostatically
Nano Research Nano Res DOI 10.1007/s12274-015-0729-7 Tunable diameter electrostatically-formed nanowire for high sensitivity gas sensing Alex Henning1, Nandhini Swaminathan1 , Andrey Godkin1, Gil Shalev1, Iddo Amit1, and Yossi Rosenwaks 1 () Nano Res., Just Accepted Manuscript • DOI 10.1007/s12274-015-0729-7 http://www.thenanoresearch.com on January 28, 2015 © Tsinghua University Press 2015 Just Accepted This is a “Just Accepted” manuscript, which has been examined by the peer-review process and has been accepted for publication. A “Just Accepted” manuscript is published online shortly after its acceptance, which is prior to technical editing and formatting and author proofing. Tsinghua University Press (TUP) provides “Just Accepted” as an optional and free service which allows authors to make their results available to the research community as soon as possible after acceptance. After a manuscript has been technically edited and formatted, it will be removed from the “Just Accepted” Web site and published as an ASAP article. Please note that technical editing may introduce minor changes to the manuscript text and/or graphics which may affect the content, and all legal disclaimers that apply to the journal pertain. In no event shall TUP be held responsible for errors or consequences arising from the use of any information contained in these “Just Accepted” manuscripts. To cite this manuscript please use its Digital Object Identifier (DOI®), which is identical for all formats of publication. 1 TABLE OF CONTENTS (TOC) Tunable Diameter Electrostatically-formed Nanowire for High Sensitivity Gas Sensing Alex Henning, Nandhini Swaminathan, Andrey Godkin, Gil Shalev, Iddo Amit, and Yossi Rosenwaks* Department of Physical Electronics, School of Electrical Engineering, Tel-Aviv University, Ramat-Aviv 69978, Israel Page Numbers. The font is ArialMT 16 (automatically inserted by the publisher) Tunable diameter electrostatically-formed nanowire towards a highly sensitive and robust room temperature gas sensing device. 1 Nano Res DOI (automatically inserted by the publisher) Research Article Tunable Diameter Electrostatically-formed Nanowire for High Sensitivity Gas Sensing Alex Henning1, Nandhini Swaminathan1, Andrey Godkin1, Gil Shalev1, Iddo Amit1, and Yossi Rosenwaks1 () 1 Department of Physical Electronics, School of Electrical Engineering, Tel-Aviv University, Ramat-Aviv 69978, Israel Received: day month year / Revised: day month year / Accepted: day month year (automatically inserted by the publisher) © Tsinghua University Press and Springer-Verlag Berlin Heidelberg 2011 ABSTRACT We report on an electrostatically-formed nanowire (EFN) based sensor with tunable diameters in the range of 16 nm to 46 nm and demonstrate an EFN based field-effect transistor as a highly sensitive and robust room temperature gas sensor. The device was carefully designed and fabricated using standard integrated-processing to achieve the 16 nm EFN and used for sensing without any surface modification. The EFN effective diameter was determined using Kelvin probe force microscopy accompanied by three-dimensional electrostatic simulations. We show that the EFN transistor is capable of detecting 100 parts per million of ethanol gas with bare SiO2. KEYWORDS Gas Sensing, Silicon Nanowires, KPFM, Electrostatic confinement, Multiple gate transistor Introduction Field-effect transistors (FETs) based on one-dimensional nanostructured materials have emerged as most promising candidates for miniature chemical sensors in comparison to the planar FETs [1]. In particular, Silicon Nanowire (SiNW) based FETs were demonstrated as highly sensitive and selective chemical sensors operating at room temperature (RT) [2–5]. Single crystalline SiNWs are fabricated via bottom-up or top-down methods with uniform spatial dimensions and high carrier mobility [6–11]. Predominantly, FETs based on arrays of SiNWs, usually modified with molecular groups, have been reported to be highly sensitive and selective to volatile organic compounds (VOCs) [2,4,12–18]. Due to the high surface-to-volume ratio of Si NWs, surface states have a large impact on the device performance and often require surface passivation. Although the top-down approach has less severe integration issues with the complementary metal-oxide-semiconductor (CMOS) technology compared to chemically grown NWs ———————————— Address correspondence to Yossi Rosenwaks, [email protected] 2 [19,20], it involves the lithographic techniques. use of sophisticated We present a robust electrostatically-formed nanowire (EFN) based sensor whose tunable nanowire diameter was determined by Kelvin probe force microscopy (KPFM) measurements supported by three-dimensional (3-D) electrostatic simulations. Detection of ethanol gas has been used as an example to demonstrate the application of the EFN device as a gas sensor. The detection sensitivity increases by a factor of 27 as the EFN effective diameter is reduced from 46 nm to 16 nm. We show that the 16 nm EFN device is capable of detecting ethanol down to a concentration of 100 parts per million (ppm), which is among the lowest reported values for nanostructured gas sensors without surface modification. Paska et al. demonstrated a limit-of-detection (LOD) of 60 ppm for ethanol using SiNW FETs with an organic surface modification [16]. Wu et al. showed 40 ppm LOD for ethanol with Sb-doped SnO2 NWs at RT [21]. Recently, Chu et al. demonstrated a 0.5 ppm detection limit for ethanol at RT using NW FETs modified with iron porphyrin attached to organic linker molecules [5]. Carbon nanotube (CNT) based FETs are also used as highly sensitive devices. Someya et al. showed an LOD of about 1300 ppm for ethanol with bare CNT based sensors [22]. Mirica et al. demonstrated response to 700 ppm of ethanol with CNT based sensors at RT modified with various selectors [23]. Liang et al. used CNTs coated with a thin SnO2 layer to detect ethanol down to 10 ppm with a sensitivity of 1.8 [24]. Chen et al. achieved a high sensitivity for 10 ppm of ethanol at RT for 1-D core/shell nanostructures (CNT/SnO2) [25]. The EFN device was fabricated using standard CMOS processing and demonstrates higher signal-to-noise ratio compared to the conventional NW based FETs. The EFN concept was first introduced by Shalev et al. in 2013 [26], who demonstrated a surface modified EFN (25 nm in width) based biosensor for the detection of femtomolar protein concentrations. Basically, the EFN is a nanowire-like conducting channel that is tuned to the nanometer size electrostatically post fabrication by appropriate gate biasing. The EFN device resembles the silicon-on-insulator (SOI) four-gate field-effect transistor (G4-FET), developed in 2002 [27,28] that emerged from the volume inversion SOI MOSFET [29]. Results and discussion EFN FORMATION AND ELECTRICAL CHARACTERIZATION. The EFN device (Fig. 1 a) is composed of a doped silicon region surrounded by four gates, a back gate (biased with V BG), two lateral junction gates (biased with V JG1 and V JG2) and a top dielectric that functions as a molecular gate. The electron accumulated channel between the source and drain is confined to a nanowire by appropriate biasing of V JG1, V JG2 and V BG. The active area is passivated with 6 nm thick thermal SiO2 that can be activated and modified for enhanced analyte adsorption with a self-assembled monolayer. The thickness and purity of the top oxide (SiO2) layer are important parameters for FET based sensors. The EFN device is a field-effect device where variations of the drain current with respect to the surface potential, Φs, define the gain, g s = dID/dΦs = (W/L)Ctox µeVD, where W and L are the respective width and length of the channel, Ctox is the top oxide layer capacitance and µe is the electron mobility. Therefore, a thinner gate dielectric results in greater Ctox and thus a higher gain. The cross-section along the short axis of the device (Fig. 1 b) depicts a scheme for the electron accumulated EFN channel (dark blue). Various nanowire configurations, each with a particular shape and effective diameter of the cross-sectional area are obtained with appropriate biasing of the surrounding gates. No nanometer features are defined during the fabrication, and the nanometer scaling of the EFN device is performed electrostatically post fabrication. 3 Figure 1 Schematic illustration of an EFN device. (a) Different contact regions and the channel region are defined by specific doping implants, assigned with n+, n and p+. A thermal SiO2 layer with a thickness of 6 nm covers the active sensing area. The EFN device is biased according to the electrical circuit. (b) Schematic cross-section along the y-axis of the device showing one possible configuration of the electrostatically shaped nanowire with a volatile organic compound (ethanol) bound to the active area of the device. Figure 2 (a) depicts a top scanning electron microscopy (SEM) image of the EFN device including the contact regions of source, drain and junction gates. The contact regions were designed large enough to be contacted with microprobes. Figure 2 (b) is a high magnification SEM image of the n-doped path in the center of the device. The nanowire is formed inside this ≈ 650 nm wide n-doped area, located in-between the two p-doped regions that appear bright in the SEM contrast. The distance between the two p-doped regions is the critical (spatial) dimension for the photolithography masks. Secondary electrons are sensitive to the surface dopant distributions providing a few nanometers lateral resolution [30] and allowed us to determine the width of the n-type doped region from the measured image (Fig. 2 b). The atomic force microscopy (AFM) topographic profile of the SiO2 surface within the 100 µ m2 sensing area (Fig. 2 c top) reveals a root mean square roughness of below 1 nm. The electron conductive channel is formed inside the n-doped silicon below the gate oxide. Figure 2 Scanning electron microscopy image of (a) a full EFN device with contact areas and (b) the active area in the center of the device where the EFN is located. In this square window the 6 nm thick gate dielectric is directly exposed to the analytes while the surrounding is passivated with a ≈ 40 nm thick dielectric layer. The ≈ 650 nm wide n-doped region appears darker in the SEM image and corresponds to the distance between the metallurgical junctions of the p-n-p structure. (c) Measured AFM topography (red line) is added on top of a schematic depth profile of the active area in the square window. 4 The complete EFN device process was simulated with a 3-D device simulator (Synopsys TCAD Sentaurus, Mountain View, CA, USA) taking into account all the fabrication processes including the actual ion implantations and thermal annealing steps. For each of the simulation mesh points, the Poisson and continuity equations are numerically solved. Electron acceptor and donor type interface trap states located at the gate-silicon interfaces with a concentration of 1 × 10 12 cm−2 were taken into account, whereas the contact resistances and the ambient air were neglected in the simulations. Figure 3 (a) shows the measured (black squares) and simulated (red circles) drain current, and the extracted effective diameter, De ff, (blue triangles) as a function of the side gate voltages, ID−V JG12, where V JG12 = V JG1 = V JG2. De ff of the EFN channel is defined as the full width at half maximum (FWHM) of the electron density distribution, ρ(r), within the n-doped Si across the p-n-p junction (Fig. 3 b) and was obtained by comparing the measured and simulated I−V characteristics (Fig. 3 a). By gradually applying more negative bias, V JG12, on both side gates, the drain current, ID, of the electron accumulated channel formed between source and drain is reduced and its De ff decreased (Fig. 3 a). Figure 3 The EFN effective diameter, Deff, is reduced to a few nanometers by reversed junction gate biasing. (a) Simulated and measured drain current-side gate bias (ID − VJG12) characteristics for the EFN is shown in a semi-logarithmic plot. Deff was estimated from 3-D electrostatic simulations. (b) The electron density distributions across the EFN correspond to 3 possible configurations and are extracted from 3-D simulations. (c) Measured drain current-drain voltage (ID − VD) characteristics are depicted in a semi-logarithmic plot; the dashed line represents the pinch-off voltage, VP . It is evident that the EFN transistor on/off ratio, ION/IOFF, is about 1 ×106. Below V JG12 ≈ −1.2 V, the current sharply decreases as the depletion regions span the entire conduction channel leaving a small electron accumulation region. De ff of the EFN cross-sectional area is found to be 46 nm for V JG12 = 0 V and 16 nm for V JG12 = −1.6 V. For V JG12 < −1.6 V, the electron density in the EFN drops below 3 × 10 15 cm−3 which corresponds to the detection limit of our measurement system. With more negative side gate voltages (V JG12 < −1.6 V) the electron-accumulated channel is pushed towards the device surface. In this case, the circular EFN shape turns to be elliptical maintaining a constant De ff of 16 nm, which corresponds to the transverse diameter of the elliptical cross-sectional area. We define the EFN as fully depleted when the electron density inside the channel drops by two orders of magnitude, from 3 × 10 17 cm−3 to 3 × 10 15 cm−3 with a corresponding current below the detection limit ( ≈ 5 pA). Accordingly, the EFN is fully depleted below V JG12 ≈ −1.6 V corresponding to De ff ≈ 16 nm as evident from Figure 3 (a). Pinch-off occurs due to the tapered shape of the electron-conducting path, which is a consequence of the drain-source potential drop along the channel. In a regular junction gate FET, the pinch-off voltage, VP , is the applied drain-source voltage for a certain gate voltage at which the drain current saturates. In the EFN device, V P is the source-drain voltage V D, for a particular V JG12 at which ID saturates because the two depletion regions from both sides of the channel are crossing each other as shown in the CPD measurement of an EFN device under operation (Fig. 4a, V JG12 = -1 V). 5 Depending on V JG12, the pinch-off voltage (indicated by dashed line Fig. 3 c) is in the range of V D = 0.1 to 0.8 V. It is evident from the ID-V D characteristics that the transistor operates in the linear Ohmic regime for V D below V P while for V D above VP , the transistor operates in the saturation regime and its current is nearly constant. 4 b, V JG12 = −2 V) the measured current also drops to zero (Fig. 3 a). At V JG12 = 0 V, the current linearly increases as a function of V D (Fig. 3 c) and the nanowire can be treated as a cone-shaped and uniformly doped conductor. The cross-sectional area, A, and resulting De ff are estimated using Ohm’s law (Eq. 1) [33]: KELVIN PROBE FORCE MICROSCOPY OF AN EFN DEVICE. KPFM measures the contact potential difference (CPD) between the AFM tip and a sample with nanometer spatial resolution and meV sensitivity [31,32] where the CPD is a direct measure of the sample Fermi level energy. Figure 4 (a) represents the CPD images of an EFN under operation for three different biasing configurations: V JG12 = 0 V, −1 V and −2 V at V D = 1 V and V BG = 0 V. The extracted CPD profiles along the EFN channel (Fig. 4 b) from source to drain (indicated by the dashed arrow) emphasize the effect of a more negative V JG12: a CPD increase in the conductive channel indicates a larger potential barrier between the source and drain. For negative V JG12, the conductive channel is more depleted of electrons and therefore the measured CPD is higher (more p-type). At V JG12 = −2 V the EFN is fully depleted and the depletion regions on either side of the EFN overlap (Fig. 4 a). As the energy barrier between the source and drain of a depleted EFN becomes too large (Fig. J = q µe n(x) ·d|CPD|/dx (1) J = ID/A is the current density, Ex = d|CPD|/dx is the local electric field, n(x) is the free carrier density inside the EFN, µ e is the electron mobility and q is the elementary charge. By differentiating the measured CPD profile along the EFN, Ex is obtained. The doping density was measured by time-of-flight secondary ion mass spectrometry (TOF-SIMS) and equals n = 4.0 ± 0.2 × 10 17 cm−3 which corresponds to µ e = (430 ± 10) cm2/Vs. ID was measured during each CPD measurement. Hence, all parameters except from A are known and the diameter was calculated along the EFN axis (Fig. 4 c). The error bars result from the measurement uncertainties for doping density, mobility, and CPD (± 5 mV). Due to the source-drain potential difference that causes pinch-off, the diameter decreases along the nanowire axis resembling a cone-like shape as schematically shown in Figure 4 c. 6 Figure 4 (a) CPD images of the EFN active area and (b) CPD profiles along the EFN channel from source to drain for three different cases: undepleted, partially depleted and fully depleted. VBG was maintained at 0 V. (c) The EFN diameter in axial direction along the nanowire was extracted from the measured CPD profile at V JG12 = 0 V. In order to demonstrate the reliability of this method to estimate the diameter, we have characterized an EFN device with a larger channel. Figure 5 (a) shows the ID-V D characteristics of the large EFN for four different side gate voltages, V JG12 = 0 V, -0.5 V, -1 V and -1.5 V. Compared with the I-V characteristics of the narrow EFN device (Fig. 3 c), the saturation (at VP ) is reached for higher source-drain-voltages. De ff was determined for four side gate voltages while applying a constant drain bias (V D = 0.5 V) indicated by the red circles in Figure 5 (a). The effective width was calculated from the CPD profiles from source to drain along the NW (Fig. 5 b) by using the slopes of the CPD profiles between 2 and 3 µ m in Eq. 1. In this manner, the values of De ff are equal to 105 nm, 85 nm, 67 nm and 40 nm for V JG12 = 0 V, -0.5 V, -1 V, -1.5 V, respectively. Figure 5 (a) ID-VD characteristics for a large channel EFN device for 4 different side gate voltages and corresponding (b) CPD profiles along the EFN channel from source to drain at VD = 0.5 V and VBG = 0 V. ETHANOL VAPOR SENSING WITH AN EFN DEVICE. The sensitivity of the EFN device for ethanol detection is quantified through the drain current change here defined as ∆I/I0 = (I0 - Ie th)/I0, where I0 and Ie th are the drain currents in pure nitrogen and ethanol with nitrogen as carrier gas, respectively. Figure 6 (a) shows the sensitivity of the device as a function of ethanol concentrations for side gate voltages, V JG12 = 0 V, −0.9 V, −1.2 V and −1.5 V and a back gate voltage of V BG = −6 V. These side gate voltages correspond to an effective EFN diameter varied from 46 nm to 16 nm, as represented by the schematic NW cross-sections to the right of Figure 6 (a). 7 Figure 6 Sensitivity plot as a function of ethanol concentration in ppm range at VBG = −6 V and VD = 1 V. Different curves correspond to VJG12 = 0 V, −0.9 V, −1.2 V and −1.5 V each voltage is equivalent to a different effective diameter represented by the semi-spherical cross-sections on the right. The Inset shows the logarithmic plot of the ID−VBG characteristics for different V JG12. Dotted curves correspond to the N2 atmosphere and the solid curves correspond to 1100 ppm ethanol exposure on the EFN device. (b) The plot of the drain current as a function of the ethanol concentration shows a linear behavior within the measurement uncertainties. The sensitivity increases with the concentration for all curves (for each V JG12). Furthermore, at each concentration, the sensitivity increases with decreasing V JG12 corresponding to a narrower channel. It is evident from Figure 6 (a) that the EFN device is sensitive to ethanol concentrations as low as 100 ppm when V JG12 < −0.9 V and V BG = −6 V. Figure 6 (b) shows the sensor response as a function of the ethanol concentration for the narrowest EFN (16 nm) showing a linear behavior. The error bars result from the device noise current and uncertainty of the adjusted ethanol vapor concentration. The EFN device can be reused following mild heating after which the ethanol molecules are desorbed. Figure 7 shows the drain current - backgate characteristics (ID-V BG) for three different cases: before sensing, after sensing and after heating. Figure 7 Drain current - backgate characteristics (ID-VBG) for the EFN device before (green triangles) and after long-term exposure to 1000 ppm of ethanol (black squares), and after regeneration (red circles), achieved by heating to 70 °C. The surface charge density can be estimated by using the basic relation of the threshold voltage shift, ∆V th = − (QSS tbox)/(ε0εox), for a standard MOS capacitor where QSS is the surface charge density, tbox is the back oxide layer thickness, ε0 is the vacuum permittivity and εox is the relative dielectric constant [34]. The measured threshold-voltage shift, ∆V th = 2.1 V, following ethanol adsorption (exposure to 1000 ppm), corresponds to QSS = 2.5 × 10 11 cm-2. Figure 8 shows the transconductance, gm, and sensitivity as a function of V JG12 obtained in the following two cases: (a) measurements with the EFN device at 1100 ppm ethanol exposure (b) simulation for 10 trapped electrons fixed on top (center) of the EFN channel surface representing a charged analyte molecule. In this work, gm is calculated as: ∂ID/∂V BG| VD=1V. As a consequence of the narrower channel due to more negative side gate voltages, the absolute change in ID becomes smaller. Hence, gm decreases with higher reversed side gate voltages (Fig. 8). 8 voltage where the transconductance curve is peaked. But this is not the case for the EFN device; here, the enhanced sensitivity is a direct result of the vertical and lateral size and shape of the channel tuned by appropriate biasing of V BG and V JG12, respectively. Conclusions Figure 8 Transconductance and logarithmic plot of sensitivity as a function of Deff controlled with reversed gate voltages V JG12 for VD = 1 V and VBG = 2.8 V and 10.8 V for (a) experimental results of the EFN sensing towards 1100 ppm ethanol and (b) simulated results for 10 electrons placed in the center of the EFN. Comparing the measurements with simulations, it is observed that the influence of the adsorbed ethanol molecules on the EFN characteristics is equivalent to that of the localized negative charges at the channel center. The negative surface charge causes electron depletion in the EFN hence reducing the drain current. The order of magnitude difference in the y-axis of Figure 8 (a) and Figure 8 (b) is due to two reasons: First, the surrounding medium for the EFN in the simulations is vacuum while in experiments, it is nitrogen; Secondly, trapped oxide charges in the top dielectric screen the electric field and were not taken into account in the simulations. The increase in the sensitivity with smaller De ff (more negative V JG12) can be explained by the influence of the adsorbed ethanol molecules on the electron density distribution of the EFN (Fig. 3 b). Adsorbed molecules modify the surface charge distribution and consequently induce a change in the surface potential; the smaller the EFN, the more it is affected by such a surface potential change. Hence, the increase in the sensitivity is a direct result of a smaller conducting channel when V JG12 is decreased. In addition, Figure 8 indicates that while sensitivity is high for more negative values of V JG12, gm is maximal at 0 V. Typically, the sensitivity of a FET-type sensor strongly depends on gm of the transistor. The device is most sensitive for the gate In summary, we have demonstrated an electrostatically formed nanowire with a tunable effective width down to 16 nm. The electrical properties of the device and the nanowire channel dimensions were simulated using a 3-D electrostatic simulator and were found to be in excellent agreement with KPFM and I − V measurements. The device was capable of detecting 100 ppm of ethanol vapor with a bare SiO2 surface. The EFN device being a low-cost (CMOS-compatible), robust and highly sensitive gas sensor, paves the way for future ultra-compact electronic devices. Work is in progress to achieve selectivity and increase the device sensitivity by surface modifications, using EFN arrays and signal processing. Materials and Methods EFN DEVICE FABRICATION. The EFN transistors were fabricated by a semiconductor foundry (TowerJazz, Israel - Migdal Haemek) in a CMOS process with 4 masks to implant the different dopant regions for the channel, source-drain and junction gate contacts. The actual doping densities, blanket Arsenic of 4 × 10 17 cm−3, junction gate Boron of 2 × 1020 cm−3 and source-drain Arsenic of 7 × 10 19 cm−3, were determined post fabrication by time-of-flight secondary ion mass spectrometry (TOF-SIMS). Boron doped 8 inch SOI wafers with a doping density of 1.5 × 10 14 cm2 and an SOI thickness of 150 nm were used. The thickness of the buried SiO2 is 1 µ m. The thermal SiO2 gate dielectric was formed at 1200 °C. The lowest spatial dimension in the process ((540 ± 20) nm) was given by the distance between the two metallurgical junctions within the active area. Devices were diced to 1 cm2 squares and Ti/Au contacts were manufactured by optical lithography and subsequent metal evaporation. ELECTROSTATIC DEVICE SIMULATIONS. A three-dimensional (3-D) finite-element device 9 simulator (Synopsys TCAD Sentaurus, Mountain View, CA, USA) was used in order to solve the Poisson equation, and the hole and electron continuity equations for each mesh. The measured doping density depth profiles (TOF-SIMS) within the silicon served as input for 3-D electrostatic simulations. Drift-diffusion transport model together with Boltzmann statistics were assumed throughout the device and the Masetti model for doping-dependent mobility was used in order to account for impurity scattering [35]. Drain, source, backgate and side gate contacts were defined and forced the respective biasing as boundary conditions. The material constants of silicon were taken from the literature [36]. The source-drain current was simulated for different configurations of backgate, sidegate and drain voltages. For the qualitative charge sensing, 10 elementary charges were placed on top of the SiO2 gate dielectric in the lateral and transversal center of the channel. The elementary charges were placed inside an imaginary cube with side dimensions of 10 nm. The charged cube should emulate the effect of a big sized molecule. This simplifies the problem as in reality molecules rather represent dipoles. ELECTRICAL CHARACTERIZATION AND GAS SENSING. Current-voltage characteristics, both as a function of drain electrode bias (ID−VD), backgate electrode bias (ID−V BG) and junction gate electrodes (ID−V JG12), were performed using semiconductor parameters analyzer (B1500A, Agilent). Sensing of volatile ethanol was done in a controlled nitrogen (99.999 % purity) atmosphere in a sealed metallic gas chamber connected to a gas dilution system. Ethanol gas was generated in a bubbler system and diluted with N2 and mass flow controllers. A reference sensor (ppbRAE 3000, RAE Systems) was connected to the gas chamber in order to verify the analyte concentration inside the chamber down to 100 ppb level. Sensing was performed by measuring and comparing the I−V characteristics with and without different concentrations of ethanol. The EFN device was cleaned and hydroxylated by the SC-1 treatment that involves immersion of the device in NH4OH:H2O2:H2 O (1:1:5, v/v/v) at 70 °C for 10 min. The device was then rinsed thoroughly in DI water several times and blow dried with N2. KELVIN PROBE FORCE MICROSCOPY. Amplitude modulation KPFM was carried out with a commercial AFM (Dimension Edge, Bruker Inc.) inside a nitrogen glove box with less than 1 ppm H2O. The CPD was measured simultaneously with the topographic signal at an effective tip sample distance of 5 to 10 nm during scanning. The topographic height was obtained by maintaining the amplitude of the first cantilever resonance (f 1st ≈ 75 kHz) at a predefined amplitude set point of approximately 5 to 20 nm. The CPD was determined by compensating the ac component of the electrostatic force, FES, at angular frequency ω with an applied dc voltage (= CPD) in a feedback control loop. To separate topographic from CPD signal, increase the sensitivity, and minimizing probe convolution effects, the ac electrostatic force component was generated at the second resonance [37,38], f2nd ≈ 450 kHz, of the cantilever by applying an ac voltage of about 500 mV. Highly conductive cantilevers with Pt/Ir coating (PPP EFM, Nanosensors) were used for KPFM. TOF-SIMS. Doping depth profiles with a surface sensitivity of 2 nm were obtained with a TOF-SIMS instrument (2100 TRIFT II, PHI). Briefly, a pulsed primary ion beam is used to desorb and ionize species from a sample surface. The resulting secondary ions are accelerated into a mass spectrometer, where they are mass analyzed by measuring their time-of-flight from the sample surface to the detector. Acknowledgements We are very grateful to Yakuv Roizin, Alexey Heiman, Miriam Buchbinder and Noel Berkovitch from TowerJazz for device fabrication and helpful discussions. We acknowledge the ’Pearl of Wisdom’ foundation. AH acknowledges the support of the Tel Aviv University Center for Nanoscience and Nanotechnology. References [1] Zhou, K. B.; Wang, X.; Sun, X. M.; Peng, Q.; Li, Y. D. Enhanced catalytic activity of ceria nanorods from well defined reactive crystal planes. J. Catal. 2005, 229, 206–212. [1] Patolsky, F.; Lieber, C. M. Nanowire nanosensors. Mater. Today 2005, 8, 20–28. [2] Cui, Y.; Wei, Q.; Park, H.; Lieber, C. M. Nanowire 10 nanosensors for highly sensitive and selective detection of biological and chemical species. Science 2001, 293, 1289–1292. [3] [4] [5] [6] [7] [8] [9] Zheng, G.; Patolsky, F.; Cui, Y.; Wang, W. U.; Lieber, C. M. Multiplexed electrical detection of cancer markers with nanowire sensor arrays. Nat. Biotechnol. 2005, 23, 1294–1301. Paska, Y.; Stelzner, T.; Christiansen, S.; Haick, H. Enhanced sensing of nonpolar volatile organic compounds by silicon nanowire field effect transistors. ACS nano 2011, 5, 5620–5626. Chu, C. J.; Yeh, C. S.; Liao, C. K.; Tsai, L.-C.; Huang, C.-M.; Lin, H.-Y.; Shyue, J.- J.; Chen, Y.-T.; Chen, C.-D. Improving nanowire sensing capability by electrical field alignment of surface probing molecules. Nano Lett. 2013, 13, 2564–2569. Morales, A. M.; Lieber, C. M. A laser ablation method for the synthesis of crystalline semiconductor nanowires. Science 1998, 279, 208–211. Cui, Y.; Zhong, Z.; Wang, D.; Wang, W. U.; Lieber, C. M. High performance silicon nanowire field effect transistors. Nano Lett. 2003, 3, 149–152. Elibol, O.; Morisette, D.; Akin, D.; Denton, J.; Bashir, R. Integrated nanoscale silicon sensors using top-down fabrication. Appl. Phys. Lett. 2003, 83, 4613–4615. Yang, C.; Zhong, Z.; Lieber, C. M. Encoding electronic properties by synthesis of axial modulation-doped silicon nanowires. Science 2005, 310, 1304–1307. Ultraselective Detection in the Gas Phase. Nano Lett. 2014, 14, 933–938. [19] Stern, E.; Klemic, J. F.; Routenberg, D. A.; Wyrembak, P. N.; Turner-Evans, D. B.; Hamilton, A. D.; LaVan, D. A.; Fahmy, T. M.; Reed, M. A. Label-free immunodetection with CMOS-compatible semiconducting nanowires. Nature 2007, 445, 519–522. [20] Park, I.; Li, Z.; Pisano, A. P.; Williams, R. S. Top-down fabricated silicon nanowire sensors for real-time chemical detection. Nanotechnology 2010, 21, 015501. [21] Wu, J. M. A room temperature ethanol sensor made from p-type Sb-doped SnO2 nanowires. Nanotechnology 2010, 21, 235501. [22] Someya, T.; Small, J.; Kim, P.; Nuckolls, C.; Yardley, J. T. Alcohol vapor sensors based on single-walled carbon nanotube field effect transistors. Nano Lett. 2003, 3, 877–881. [23] Mirica, K. A.; Azzarelli, J. M.; Weis, J. G.; Schnorr, J. M.; Swager, T. M. Rapid prototyping of carbon-based chemiresistive gas sensors on paper. Proc. Natl. Acad. Sci. 2013, 110, E3265–E3270. [24] Liang, Y.; Chen, Y.; Wang, T. Low-resistance gas sensors fabricated from multiwalled carbon nanotubes coated with a thin tin oxide layer. Appl. Phys. Lett. 2004, 85, 666–668. [25] Chen, Y.; Zhu, C.; Wang, T. The enhanced ethanol sensing properties of multi-walled carbon nanotubes/SnO2 core/shell nanostructures. Nanotechnology 2006, 17, 3012. [11] Schmidt, V.; Wittemann, J.; Gösele, U. Growth, thermodynamics, and electrical properties of silicon nanowires. Chem. Rev. 2010, 110, 361–388. [26] Shalev, G.; Landman, G.; Amit, I.; Rosenwaks, Y.; Levy, I. Specific and label-free femtomolar biomarker detection with an electrostatically formed nanowire biosensor. NPG Asia Mater. 2013, 5, e41. [27] Cristoloveanu, S.; Blalock, B.; Allibert, F.; Dufrene, B.; Mojarradi, M. The four-gate transistor. In Proceedings of the European Solid-State Device Research Conference. 2002, pp 323–326. [12] McAlpine, M. C.; Ahmad, H.; Wang, D.; Heath, J. R. Highly ordered nanowire arrays on plastic substrates for ultrasensitive flexible chemical sensors. Nat. Mater. 2007, 6, 379–384. [28] Blalock, B. J.; Cristoloveanu, S.; Dufrene, B. M.; Allibert, F.; Mojarradi, M. M. The multiple-gate MOS-JFET transistor. Int. J. High Speed Electron. Syst. 2002, 12, 511–520. [13] Engel, Y.; Elnathan, R.; Pevzner, A.; Davidi, G.; Flaxer, E.; Patolsky, F. Supersensitive detection of explosives by silicon nanowire arrays. Angew. Chem. Int. Ed. 2010, 49, 6830–6835. [29] Balestra, F.; Cristoloveanu, S.; Benachir, M.; Brini, J.; Elewa, T. Double-gate silicon- on-insulator transistor with volume inversion: A new device with greatly enhanced performance. IEEE Electron Device Lett. 1987, 8, 410–412. [30] Grunbaum, E.; Barkay, Z.; Shapira, Y.; Barnham, K.; Bushnell, D.; Ekins-Daukes, N.; Mazzer, M.; Wilshaw, P. The electric field and dopant distribution in p-i-n structures observed by ionisation potential (dopant contrast) microscopy in the HRSEM. In Microscopy of Semiconducting Materials. Cullis, A. G., Hutchison J. L., Eds.; Springer: Berlin Heidelberg, 2005, pp 503–506. [10] Tong, H. D.; Chen, S.; van der Wiel, W. G.; Carlen, E. T.; van den Berg, A. Novel top-down wafer-scale fabrication of single crystal silicon nanowires. Nano Lett. 2009, 9, 1015–1022. [14] Niskanen, A.; Colli, A.; White , R.; Li, H.; Spigone, E.; Kivioja, J. Silicon nanowire arrays as learning chemical vapour classifiers. Nanotechnology 2011, 22, 295502. [15] Cao, A.; Sudhölter, E. J.; de Smet, L. C. Silicon Nanowire-Based Devices for Gas-Phase Sensing. Sensors 2013, 14, 245–271. [16] Paska, Y.; Stelzner, T.; Assad, O.; Tisch, U.; Christiansen, S.; Haick, H. Molecular gating of silicon nanowire field-effect transistors with nonpolar analytes. ACS Nano 2011, 6, 335–345. [17] Wang, B.; Haick, H. Effect of functional groups on the sensing properties of silicon nanowires toward volatile compounds. ACS Appl. Mater. Interfaces 2013, 5, 2289–2299. [18] Wang, B.; Cancilla, J. C.; Torrecilla, J. S.; Haick, H. Artificial Sensing Intelligence with Silicon Nanowires for [31] Nonnenmacher, M.; Oboyle, M.; Wickramasinghe , H. Kelvin probe force microscopy. Appl. Phys. Lett. 1991, 58, 2921–2923. [32] Glatzel, T. In Kelvin Probe Force Microscopy; Sadewasser, S., Glatzel, T., Eds.; Springer Series in Surface Sciences; Springer: Berlin Heidelberg, 2011; pp 289–327. [33] Koren, E.; Rosenwaks, Y.; Allen, J.; Hemesath, E.; Lauhon, L. Nonuniform doping distribution along silicon nanowires 11 measured by Kelvin probe force microscopy and scanning photocurrent microscopy. Appl. Phys. Lett. 2009, 95, 092105. [34] Shaya, O.; Shaked, M.; Usherenko, Y.; Halpern, E.; Shalev, G.; Doron, A.; Levy, I.; Rosenwaks, Y. Tracing the mechanism of molecular gated transistors. J. Phys. Chem. C 2009, 113, 6163–6168. [35] Masetti, G.; Severi, M.; Solmi, S. Modeling of carrier mobility against carrier concentration in arsenic-, phosphorus-, and boron-doped silicon. IEEE Trans. Electron Devices 1983, 30, 764–769. [37] Kikukawa, A.; Hosaka, S.; Imura, R. Silicon pn junction imaging and characterizations using sensitivity enhanced Kelvin probe force microscopy. Appl. Phys. Lett. 1995, 66, 3510–3512. [38] Glatzel, T.; Sadewasser, S.; Lux-Steiner, M. C. Amplitude or frequency modulation- detection in Kelvin probe force microscopy. Appl. Surf. Sci. 2003, 210, 84–89. [36] Palik, E. D. Handbook of optical constants of solids; Academic press, 1998; Vol. 3. 12
© Copyright 2026