1. No category

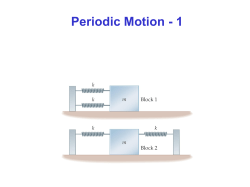
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
Chapter1: OSCILLATIONS
1. Introduction
Any motion that repeats itself in equal intervals of time is periodic, harmonic, oscillatory or vibratory
motion. Some examples are:





a mass attached to a spring, heart beat, breathing, sleeping, taking shower, eating, chewing,
blinking, drinking
a violin string, vocal cords, ear drums
a pendulum
motion of planets, stars, motion of electrons, atoms in molecules and solids
…wind (Tacoma Bridge)
Why does something vibrate/oscillate?
Whenever the system is displaced from equilibrium, a restoring force pulls it back, but it overshoots the
equilibrium position.
2. The Simple Harmonic Motion (SHM)
If a particle moves under the influence of a restoring force given by
F  kx (Hooke’s Law)
(1)
then the particle oscillates about a stable equilibrium position and exhibits simply harmonic motion (or
briefly SHM). An object moves with simple harmonic motion whenever its acceleration is proportional to
its position and is oppositely directed to the displacement from equilibrium.
Here
x is the displacement of the particle from its equilibrium and
k is called the force constant.
Note that such an oscillating particle is called simple harmonic oscillator (or SHO).
An example of a SHO is a mass attached to a spring. If
we apply Newton’s second Law:
F  kx  ma
or
a
k
x
m
(2)
According to Eqn. (2), if the acceleration of a particle is
proportional to the displacement from its equilibrium
position, then particle makes SHM.
Figure 1: The direction of the force acting on the mass
m at various values of displacement x.
1
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
Quantitative Analysis:
F  ma  m
d 2x
 kx
dt 2
or
d 2x
k
 x
2
m
dt
If we say  2  k / m then
d 2x
  2 x
2
dt
(3)
Solution of this differential equation (DE) is:
x(t )  A cos(ωt   )
(4)
where A and  are constants which can be determined from initial conditions. One can show that Eqn.
(4) is the general solution of DE, Eqn. (3) such that:
dx
d
 A cos(ωt   )  ωA sin(ωt   )
dt
dt
2
d x
d
 ωA sin(ωt   )  ω 2 A cos(ωt   )
2
dt
dt
2
 ω x
If we increase the time t by 2 / ω , the function becomes:
2


x  A cos ω(t 
) 
ω


 A cos(ωt  2   )
 A cos(ωt   )
That is, the the function repeats itself after a time 2 / ω . Therefore 2 / ω is the period of the motion.
The period,
T
2
 2
m
k
(5)
1
1

T 2
k
m
(6)

and the frequency is
f 
Hence the angular frequency
ω  2f 



k
m
(7)
The constant A has a simple physical meaning. The cosine (and sine) function takes on values
from [-1,1]. Thus, Eqn. (4) has the maximum value of A called amplitude of the motion, is simply
the maximum value of the position of the particle in either the positive or negative x direction.
The quantity (ωt   ) is called phase of the motion.
The constant  is called phase constant (or initial phase angle) and, along with the amplitude A, is
determined uniquely by the position and velocity of the particle at t =0.
2
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
Figure, given below, shows the displacement x
for several SHM.
AI  A and AII  A / 2
TI  TII  T
 I   II  0
AI  AII  A
TI  T and TII  T / 2
 I   II  0
AI  AII  A
TI  TII  T
 I  0 and  II  
Another feature of the SHM is the relation between
displacement, velocity and acceleration:
x  A cos(ωt   )
v
dx
d
 A cos(ωt   )
dt
dt
 ωA sin(ωt   )
a
d 2x
d
 ωA sin(ωt   )
2
dt
dt
2
 ω A cos(ωt   )
The equation of curves are given right (for   0 )
Note that, maximum values are:
xmax  A
vmax  ωA
amax  ω A
2
Figure 2: Graphical representation of simple harmonic
motion. (a) Position versus time. (b) Velocity versus
time. (c) accelerationversus time.
3
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
and at any specified time the velocity is 90° out of phase with the position and the acceleration is 180° out
of phase with the position.
Exercise 1
A particle oscillates about x=0 on the x-axis and its displacement is given by:


x  (4m) cos t  
4

where t is measured in seconds. Find:
a) amplitude, frequency and period, b) velocity and acceleration at t=1s, c) the value of the maximum
velocity and acceleration, d) the displacements between t=0 and t=1s e) the phase at t=2s of the particle.
Exercise 2
An object of mass m attached to a spring is oscillating with a SHM. At t = 0 the displacement from its
center of oscillation, velocity and acceleration are measured as x0 = –8 cm, v0= –0.9 m/s and a0=50
m/s2 respectively. Find (a) frequency, (b) the phase constant and (c) amplitude for the motion.
4
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
A mass on a vertical spring
If we suspend a mass from a vertical spring, we have
gravity also acting on the mass. The length of the spring
increases by an amount Δl.
Taking displacements in the downward direction as
positive, the resultant force on the mass is equal to mg −
kΔl. By uisnp Newton’s Law, we write
𝐹=𝑚
𝑑2 𝑥
= 𝑚𝑔 – 𝑘(𝛥𝑙 + 𝑥)
𝑑𝑡 2
i.e.
𝑚
𝑑2 𝑥
= – 𝑘𝑥
𝑑𝑡 2
Figure 3: An oscillating mass on a vertical
given by perhaps not surprisingly, this result is identical to spring. (a) The mass at its equilibrium position.
(b) The mass displaced by a distance x from its
the equation of motion (3) of the horizontal spring:
equilibrium position.
we simply need to measure displacements from the
equilibrium position of the mass.
3. Energy Considerations in SHM
Consideration of the energy of a system is a powerful tool in solving physical problems. Energy of a SHO
can be found from:
Potential Energy
Kinetic Energy
1 2
kx
2
1
2
 k A cos(ωt   )
2
1 2
 kA cos 2 (ωt   )
2
U
K




1 2
mv
2
1
2
m ωA cos(ωt   )
2
1
mω 2 A 2 sin 2 (ωt   )
2
1 k 2
m  A sin 2 (ωt   )
2 m
1 2
kA sin 2 (ωt   )
2
Mechanical Energy:
E  K U 

1 2
kA cos 2 (ωt   )  sin 2 (ωt   )
2

since cos 2 ( )  sin 2 ( )  1
E
1 2
kA
2
(8)
*** Thus the total mechanical energy of a simple harmonic oscillator is a constant of the motion and is
proportional to the square of the amplitude., as we expect. ***
5
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
We can find a useful relation between x and v
E  K U
1 2 1 2 1 2
kA  mv  kx
2
2
2
v2 
k
A 2  x 2 or v  ω A2  x 2
m
(9)
The Figures (given below) show the potential energy, kinetic energy and mechanical energy o of SHO as
a function of time and displacement.
Exercise 3:
A 0.5 kg cube attached to a spring of force constant k = 20 N/m vibrates on a smooth surface. If the
amplitude of the motion is 3 cm. Calculate (a) the total energy of the cube, (b) maximum velocity of the
cube (c) the velocity of the cube when x = 2 cm, (d) the potential and kinetic energy at x = 2 cm (e) the
displacement of the cube when v = 0.1 m/s.
a)
d)
b)
c)
6
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
Exercise 4: The period of oscillation of an object in an ideal mass-spring system is 0.50 sec and the
amplitude is 5.0 cm. What is the speed at the equilibrium point?
At equilibrium x=0:
1
1
1
1
𝐸 = 𝐾 + 𝑈 = 𝑚𝑣 2 + 𝑘𝑥 2 = 𝑘𝐴2 = 𝑚𝑣 2
2
2
2
2
Since E=constant, at equilibrium (x = 0) the KE must be a maximum. Here v = vmax = Aω.
The amplitude A is given, but ω is not.
𝑤=
2𝜋
2𝜋
=
= 12.6 𝑟𝑎𝑑/𝑠𝑒𝑐
𝑇
0.5 𝑠
And v = vmax = Aω=(5 cm) (12.6 rad/sec)=62.8 cm/sec
Exercise 5: The diaphragm of a speaker has a mass of 50.0 g and responds to a signal of 2.0 kHz by
moving back and forth with an amplitude of 1.8×10-4 m at that frequency.
(a)
What is the maximum force acting on the diaphragm?
(b)
What is the mechanical energy of the diaphragm?
Exercise 6: The displacement of an object in SHM is given by: y(t)=( 8.00 cm) sin(1.57 rads/sec t)
What are the frequency, period maximum displacement, velocity and acceleration of the oscillations?
Comparing to y(t)= A sinωt gives A = 8.00 cm and ω = 1.57 rads/sec.
7
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
4. Applications of SHM
i–The Simple Pendulum
The simple pendulum is the idealised form that consists of a point
mass m suspended from a massless rigid rod of length L, as
illustrated in Figure. Forces acting on the ball of mass m is tension,
T and the weight W = mg. Tangential component of the weight is
the restoring force which is:
d 2s
F  mg sin   m 2
dt
where the displacement s  L . So:
 mg sin   mL
d 2
dt 2
or

d 2
g
  sin 
2
L
dt
Notice that angular acceleration,  , is not proportional to  but sin  instead. The resulting motion is
not simple harmonic. But if  is small, then we can use the approximation sin    (try it on your
calculator for  = 0.1, 0.5, 1.0 radians). We obtain
d 2
g
 
2
L
dt
(10)
For small  values, therefore, the restoring force is proportional to  , hence angular SHM.
g
L
Angular frequency:
ω
Period:
T  2
(11)
L
g
(12)
In other words, the period and frequency of a simple pendulum depend only on the length of the string
and the acceleration due to gravity. Note: A pendulum can be used to be a timer since the period is
depends only on g and L
Exercise 7: A simple pendulum of length 1 m makes 100 complete oscillations in 204 s at a certain
location. What is the acceleration of gravity at this point?
8
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
ii–The Torsional Pendulum
Figure shows a disk suspended by a wire. Point P oscillates
between Q and R with an angular amplitude of  m . The twisted
wire exerts a restoring torque on the disk to return it
equilibrium position.
This torque is given by:
  
where  is a constant depending on the property of the wire and
called torsional constant.
If we apply Newton’s second law:
  I  I
d 2
 
dt 2
or
d 2

 
2
I
dt
(13)
Thus, the disk makes angular SHM with

angular frequency:
ω
Period:
T  2
(14)
I
I
(15)

Exercise 8:
A 8 kg solid sphere with a 15 cm radius is suspended by a wire
a shown in Figure. A torque of 0.2 Nm is required to twist the
sphere through an angle of 1 rad.
(a) write the equation of motion if   0
(b) calculate the period of the oscillation
r
9
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
Exercise 9: A clock has a pendulum that performs one full swing every 1.0 sec. The object at the end of
the string weights 10.0 N. What is the length of the pendulum?
iii- Connections of springs
If two springs (with 𝑘1 𝑎𝑛𝑑 𝑘2 ) are
equivalent spring constant is
𝑘𝑒𝑞 = 𝑘1 + 𝑘2
in paralel, the
If two springs (with 𝑘1 𝑎𝑛𝑑 𝑘2 ) are in series, the
equivalent spring constant is
1
1
1
= +
𝑘𝑒𝑞 𝑘1 𝑘2
Two springs with a mass in the middle
𝑘𝑒𝑞 = 𝑘1 + 𝑘2 = 𝑘 + 𝑘 = 2𝑘
and 𝑤 =
𝑘 𝑒𝑞
𝑚
=
2𝑘
𝑚
In diatomic vibrations,
𝑤=
𝑘
𝜇
𝑚1𝑚2
where 𝜇 = 𝑚
1 +𝑚 2
is the reduced mass.
Exercise 10: Transport Tunnel
A straight tunnel is dug from Stillwater through the center of the Earth and out the other side. A physics
2014 student jumps into the hole at 9:30 am. What time does she get back to Stillwater? (Note: RE =
6.38×106 m)
10
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
iv) The LC circuit
The simplest example of an oscillating electrical circuit consists of
an inductor L and capacitor C connected together in series with a
switch as shown in Figure. The charge q on the capacitor is given
by q = VCC where C is the capacitance. When the switch is closed
the charge begins to flow through the inductor and a current
I = dq/dt flows in the circuit. The voltage across the inductor given
VL = LdI/dt . We can analyse the LC circuit using Kirchhoff’s law,
which states that. VC + VL = 0.
Therefore
𝑞
𝑑𝐼
+ 𝐿 𝑑𝑡 = 0 giving
𝐶
𝑑2𝑞
𝑑2𝑞
𝑞
+ 𝐿 𝑑𝑡 2 = 0
𝐶
𝑞
and 𝑑 𝑡 2 = − 𝐿𝐶
This equation describes how the charge on a plate of the capacitor varies with time. It is of the same form
as Equation (3) and represents SHM. The frequency of the oscillation is given directly by, ω =√1/LC.
Thus the total energy in the circuit is given by
1 2 1 2 1 2 1 𝑞2
𝐸 = 𝐿𝐼 + 𝐶𝑉𝐶 = 𝐿𝐼 +
2
2
2
2𝐶
Similarities in physics
We note the similarities between the equations for the mechanical and electrical cases
Moreover we can see a direct correspondence between the two sets of physical quantities involved:
• q takes the place of x;
• L takes the place of m;
• 1/C takes the place of k.
For example, the inductance L is the electrical analogue of mechanical inertia m. These analogies enable
us to build an electrical circuit that exactly mimics the operation of a mechanical system. This is useful
because in the development of a mechanical system it is much easier to change, for example, the value of
a capacitor in the analogue circuit than to manufacture a new mechanical component.
5. Damped Harmonic Motion (DHM)
We know that in reality, a spring won't oscillate for ever. Frictional forces will diminish the amplitude of
oscillation until eventually the system is at rest. When dissipative forces such as friction are not
negligible, the amplitude of oscillations will decrease with time. The oscillations are damped. The below
figure depicts one such system: an object attached to a spring and submersed in a viscous liquid.
To incorporate friction, we can just say that there is a frictional force ( or retarding force) that's
proportional to the velocity of the mass. This retarding force is often observed when an object moves
through air, for instance. Because the retarding force can be expressed as Fd =- b v (where b is a constant
11
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
called the damping coefficient) and the restoring force of the system is "kx, we can write Newton’s second
law as
That is:
Fd  bv  b
dx
dt
(damping force) here b is a positive constant. For
the DHM:
or
d 2x
dx
m 2  b  kx  0
dt
dt
This is the equation of a damped harmonic oscillator..
If damping force smaller than restoring than solution of DE is:
x(t )  Ae

b
t
2m
cos(ωt   )
(16)
With
𝑤=
where 𝑤0 =
𝑘
𝑚
𝑤02
𝑏
−
2𝑚
2
represents the angular frequency in the absence of a retarding force (the undamped
oscillator) and is called the natural frequency of the system.
The plot of Eqn. (16) for b =0.2 kg/m,  =0 and ω =3 rad/s is shown in Figure given below:
Depending on the degree of damping involved, there are damping cases of motion such as (i) light
damping,(ii) heavy or over damping and (iii) critical damping. Light damping is the most important case
for us because it involves oscillatory motion whereas the other two cases do not.
12
Lecture notes on OPAC102- Introduction to Acoustics



Dr. Eser OLĞAR, 2015
𝐹𝑑 = 𝑏𝑣𝑚𝑎𝑥 < 𝑘𝐴 the system is said to be underdamped. As the value of b increases, the
amplitude of the oscillations decreases more and more rapidly
When b reaches a critical value bc such that bc/2m = w0, the system does not oscillate and is said to
be critically damped. In this case the system, once released from rest at some nonequilibrium
position, approaches but does not pass through the equilibrium position.
If the medium is so viscous that the retarding force is greater than the restoring force—that is, if
𝑏
𝐹𝑑 = 𝑏𝑣𝑚𝑎𝑥 > 𝑘𝐴 and 2𝑚 > 𝑤0 —the system is overdamped. Again, the displaced system, when
free to move, does not oscillate but simply returns to its equilibrium position. As the damping
increases, the time interval required for the system to approach equilibrium also increases.
Whenever friction is present in a system, whether the system is overdamped or underdamped, the
energy of the oscillator eventually falls to zero. The lost mechanical energy is transformed into internal
energy in the object and the retarding medium.
Exercise 11: Show that time rate of change of mechanical energy for a DHM is given by
dE / dt  bv 2 and hence is always negative.
Exercise 12: A pendulum of length 1 m is released from an initial angle of 15o. After 1000 s,
its amplitude is reduced by friction to 5.5o . What is the value of b/2m ?
7. Forced Oscillations and Resonance
We have seen that the mechanical energy of a damped oscillator decreases in time as a result of the
resistive force. It is possible to compensate for this energy decrease by applying an external force that
does positive work on the system.
13
Dr. Eser OLĞAR, 2015
Lecture notes on OPAC102- Introduction to Acoustics
Energy lost in a DHM can be compensated by an external driving force doing positive work on the
system. For this case the system responds forced oscillations.
Often driving force is given by:
F  F0 cos(ωt )
with Fm amplitude of the force and ω e its angular frequency. The equation of motion becomes:
d 2x
dx
m 2  b  kx  F0 cos(ωt )
dt
dt
The system responds to the driving force by oscillating with a constant amplitude with same frequency. In
this case the frequency called resonance frequency and corresponding state of the system is called
resonance. The Solution of DE:
x(t )  A cos(ωt   )
(18)
here
A
F0
(19)
m (ω  ω 02 ) 2  (bω) 2
2
2
where ω 0  k/m is the angular frequency of the un-damped oscillator (b=0).
The forced oscillator vibrates at the frequency of the driving
force and that the amplitude of the oscillator is constant for a
given driving force because it is being driven in steady-state
by an external force. For small damping, the amplitude is
large when the frequency of the driving force is near the
natural frequency of oscillation, or when 𝑤 ≈ 𝑤0 . The
dramatic increase in amplitude near the natural frequency is
called resonance, and the natural frequency 𝑤0 is also
called the resonance frequency of the system.
Notice that: resonance of the amplitude is increasing when
damping is decreasing. The reason for large-amplitude
oscillations at the resonance frequency is that energy is
being transferred to the system under the most favorable Figure: Graph of amplitude versus frequency
conditions.
for a damped oscillator when a periodic
driving force is present.
Resonance appears in other areas of physics. For example, certain electric circuits have natural
frequencies. A bridge has natural frequencies that can be set into resonance by an appropriate driving
force. A dramatic example of such resonance occurred in 1940, when the Tacoma Narrows Bridge in the
state of Washington was destroyed by resonant vibrations. Although the winds were not particularly
strong on that occasion, the ―flapping‖ of the wind across the roadway (think of the ―flapping‖ of a flag in
a strong wind) provided a periodic driving force whose frequency matched that of the bridge. The
resulting oscillations of the bridge caused it to ultimately collapse (Fig. 15.26) because the bridge design
had inadequate built-in safety features.
14
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
http://physics.usask.ca/~pywell/p121/Images/tacoma.avi
Problems:
1.) In an engine, a piston oscillates with simple harmonic motion so that its position varies according
to the expression
𝜋
𝑥 = 5.0 𝑐𝑚 cos 2𝑡 +
6
where x is in centimeters and t is in seconds. At t = 0, find (a) the position of the piston, (b) its
velocity, and (c) its acceleration. (d) Find the period and amplitude of the motion.
2.) The position of a particle is given by the expression 𝑥 = (4.00 𝑚)𝑐𝑜𝑠(3.00 𝜋𝑡 + 𝜋) )), where x
is in meters and t is in seconds. Determine (a) the frequency and period of the motion, (b) the
amplitude of the motion, (c) the phase constant, and (d) the position of the particle at t = 0.250 s.
3.) A simple harmonic oscillator takes 12.0 s to undergo five complete vibrations. Find (a) the period
of its motion, (b) the frequency in hertz, and (c) the angular frequency in radians per second.
4.) A 7.00-kg object is hung from the bottom end of a vertical spring fastened to an overhead beam.
The object is set into vertical oscillations having a period of 2.60 s. Find the force constant of the
spring.
5.) A 0.500-kg object attached to a spring with a force constant of 8.00 N/m vibrates in simple
harmonic motion with an amplitude of 10.0 cm. Calculate (a) the maximum value of its speed and
acceleration, (b) the speed and acceleration when the object is 6.00 cm from the equilibrium
position, and (c) the time interval required for the object to move from x= 0 to x = 8.00 cm.
6.) A 1.00-kg glider attached to a spring with a force constant of 25.0 N/m oscillates on a horizontal,
frictionless air track. At t= 0 the glider is released from rest at x =-3.00 cm. (That is, the spring is
compressed by 3.00 cm.) Find (a) the period of its motion, (b) the maximum values of its speed
and acceleration, and (c) the position,velocity, and acceleration as functions of time.
7.) A block of unknown mass is attached to a spring with a spring constant of 6.50 N/m and
undergoes simple harmonic motion with an amplitude of 10.0 cm. When the block is halfway
between its equilibrium position and the end point, its speed is measured to be 30.0 cm/s.
Calculate (a) the mass of the block, (b) the period of the motion, and (c) the maximum
acceleration of the block.
8.) A 200-g block is attached to a horizontal spring and executes simple harmonic motion with a
period of 0.250 s. If the total energy of the system is 2.00 J, find (a) the force constant of the
spring and (b) the amplitude of the motion.
9.) An automobile having a mass of 1 000 kg is driven into a brick wall in a safety test. The bumper
behaves like a spring of force constant 5.00 x106 N/m and compresses 3.16 cm as the car is
brought to rest. What was the speed of the car before impact, assuming that no mechanical energy
is lost during impact with the wall?
15
Lecture notes on OPAC102- Introduction to Acoustics
Dr. Eser OLĞAR, 2015
10.)
A particle executes simple harmonic motion with an amplitude of 3.00 cm. At what
position does its speed equal half its maximum speed?
11.)
A physical pendulum in the form of a planar body moves in simple harmonic motion with
a frequency of 0.450 Hz. If the pendulum has a mass of 2.20 kg and the pivot is located 0.350 m
from the center of mass, determine the moment of inertia of the pendulum about the pivot point.
12.)
A pendulum with a length of 1.00 m is released from an initial angle of 15.0°. After 1 000
s, its amplitude has been reduced by friction to 5.50°. What is the value of b/2m?
13.)
A 10.6-kg object oscillates at the end of a vertical spring that has a spring constant of 2.05
x 104 N/m. The effect of air resistance is represented by the damping coefficient b =3.00 N. s/m.
(a) Calculate the frequency of the damped oscillation. (b) By what percentage does the amplitude
of the oscillation decrease in each cycle? (c) Find the time interval that elapses while the energy of
the system drops to 5.00% of its initial value.
14.)
A 2.00-kg object attached to a spring moves without friction and is driven by an external
force given by 𝐹 = (3.00 𝑁)𝑠𝑖𝑛(2𝜋𝑡). If the force constant of the spring is 20.0 N/m, determine
(a) the period and (b) the amplitude of the motion.
15.)
Damping is negligible for a 0.150-kg object hanging from a light 6.30-N/m spring. A
sinusoidal force with an amplitude of 1.70 N drives the system. At what frequency will the force
make the object vibrate with an amplitude of 0.440 m?
16.)
The mass of the deuterium molecule (D2) is twice that of the hydrogen molecule (H2). If
the vibrational frequency of H2 is 1.30x 1014 Hz, what is the vibrational frequency of D2? Assume
that the ―spring constant‖ of attracting forces is the same for the two molecules.
17.)
A simple pendulum with a length of 2.23 m and a mass of 6.74 kg is given an initial speed
of 2.06 m/s at its equilibrium position. Assume it undergoes simple harmonic motion, and
determine its (a) period, (b) total energy, and (c) maximum angular displacement.
References:
1) ―Physics For Scientists And Engineers‖, by Serway And Jewett, 6th Edition.
2) https://www.google.com.tr/
16