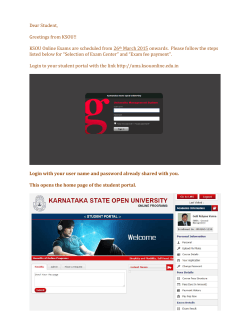
File
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Unit 4B Review on Linear Relationships KEY
Functions 8.5G
Determine whether each relation is a function. Explain.
1.
2.
3. {(5, −5), (5, 5), (6, −6), (6, 6)}
4. {(4, 11), (5, 13), (6, 15), (7, 17)}
5.
6.
x
y
25
25
50
50
−5
5
−10
10
x
y
0
1
2
3
0
1.25
2.50
3.75
7. Nora earns $15.75 per hour. Are her wages a function of the number of hours she works? Justify your
response by creating a set of ordered pairs.
Yes; (0, 0), (1, 15.75), (2, 31.5), (3, 47.25)
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Linear Functions 8.5G
Graph each function.
1. y = 2x
2. y = - 4x
3. y = x – 4
4. y = x + 3
5. y = 3x + 1
6. y = 𝑥 + 2
7. Mrs. Valdez can assemble a chair in 1 day and a table in
1
4 days. Graph the function y = 5− 𝑥 to determine how
4
many of each type of furniture Mrs. Valdez can assemble in
20 days. Is the function continuous or discrete? Explain.
8. A fitness center has set a goal to have 500 members. The
fitness center already has 150 members and adds an average
of 25 members per month. The function f(x) = 150 + 25x
represents the membership after x months. Graph the
function to determine the number of months it will take for
the fitness center to reach its membership goal. Is the
function continuous or discrete? Explain.
14 months; discrete; there cannot be partial members.
1
4
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Proportional and Non-Proportional Functions 8.5H
1. Paolo’s Portraits charges $12 per photo with no
sitting fee. The graph shows the fees for Clear
Image Studio. Determine whether the function is
proportional or non-proportional. Justify your
response.
2. Joshua earns a salary plus a commission for every
painting he sells. The equation c = 40p + 75, where
c is the commission in dollars and p is the number
of paintings, represents how much he earns.
Martin’s commissions are shown in the table.
Determine whether the function is proportional or
non-proportional. Explain.
Number of
Paintings Sold
1
2
3
Commission ($)
115
150
185
3. The table shows the cost for traveling on a toll road in Henderson. The graph shows the cost of traveling on a toll road in
Clarkson. Compare the linear functions to determine whether they are proportional or non-proportional. Justify your
response.
Henderson Toll Road Costs
Miles
Traveled
Cost ($)
10
20
30
3
6
9
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Write Equations of Functions 8.5I
Solve.
1. The Pep Club rented a shaved ice machine to sell
shaved ice as a fundraiser. They paid an initial fee and
then an hourly charge. The table shows the cost per
hour. Determine and interpret the rate of change and
initial value. Assume the relationship between the two
quantities is linear.
Number of
Hours, x
2
3
4
5
Cost ($), y
30
35
40
45
3. Marcus is a member of a theater club. He pays a
monthly fee and his movie tickets are then $5 for an
unlimited number of movies that month. The graph
shows the cost for each month. Determine the
monthly fee.
Pick two points. Find the slope or
change of y to change of x. It’s $7.50.
2. Simone planted a tomato plant and measured its height weekly. The total height at 2, 3, 4, and 5 weeks respectively
were 13, 16, 19, and 22 inches tall. How tall was the tomato plant when Simone planted it? Assume the relationship is
linear.
Create a table. Look for a pattern in the height. Then go backwards in the number of
# weeks
Height (in)
weeks until it’s at the beginning.
0
1
2
3
4
5
7
10
13
16
19
22
The plant was originally 7 in.
4. The cost of having photos taken includes a sitting fee and $12 for each portrait. The cost of 3, 6, and 9 photos
respectively is $51, $87, and $123. What is the sitting fee?
# portrait
0
1
2
3
6
9
Cost($)
15
27
39
51
87
123
Since each photo is $12, take 12 away from 51 until there’s no photo left. The
amount at zero photo is the sitting fee.
The sitting fee is $15.
NAME _____________________________________________ DATE ____________________________ PERIOD _____________
Solve Simultaneous Linear Equations
8.9A
Identify and verify the values of x and y that simultaneously satisfy each pairs of equations.
1. y = 3x + 4
y = -x – 4
2. y = 10 + 6x
y = 6x
(-2, -2)
No Solution
Write and solve a pair of simultaneous linear equations that represents the situation. Interpret the solution.
3. Alonzo and Miguel scored a total of 54 points in the basketball
game. Miguel scored four more points than Alonzo.
r+ m = 54 and m = 4 + 4
(25, 29); Miguel scored 29 and Alonzo scored 25.
4. Morgan is 15 years younger than Mrs. Santos. Their
combined age is 44.
m+ s = 44 and m = 2 – 15
(29.5, 14.5); Morgan is 14.5 and Mrs. Santos
is 29.5
5. The total number of cats and dogs at the shelter is 125.
There are 5 more cats than dogs.
c = 125 – d and c = d + 5
(60, 65); 60 dogs and 65 cats
6. Jenny won the ping-pong championship eight more times
than Gerardo. They have won a combined total of 32
championships.
J + g = 32 and j = g + 8
(12, 20); Jenny has won 20 and Gerardo has won 12.
© Copyright 2025