1. No category

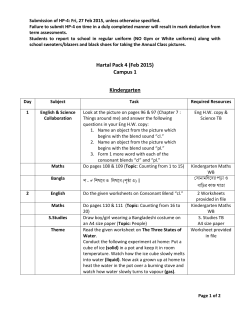
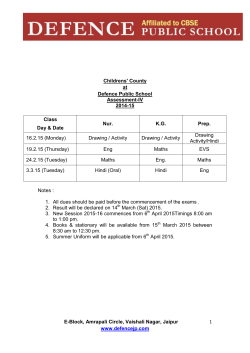
AS: Use of Maths
Algebra & Graphs
Practice sheet
Rearranging formulae
General points
•
•
•
•
•
•
•
•
The aim is to isolate the required subject at one side of the formula – all the other terms
should be at the other side.
Always do the same thing to both sides of the equation.
To ‘get rid’ of a term, do the opposite (e.g. to get rid of + mv2, subtract mv2 from both sides).
You may need to remove brackets or multiply through by a number to remove fractions
(to simplify the expression) before starting to rearrange the terms.
If the required subject is in a negative term, add this term to both sides to avoid having a
negative sign with your subject at the end.
If the subject is in the denominator of a fraction, multiply to ‘bring it to the top’.
If the subject is in a square (or square root), isolate the square (or root), then take the square
root (or square) on both sides.
If the subject appears in more than one term, bring these terms together at one side of the
equation, then write the subject outside a bracket as a common factor.
Examples
Method
d
Make t the subject of v =
t
vt = d
d
t=
v
Multiply both sides by t to ‘bring t to the top’.
Make s the subject of v 2 = u 2 + 2as
v 2 = u 2 + 2as
v 2 − u 2 = 2as
v2 − u2
s=
2a
Make u the subject of v 2 = u 2 + 2as
v 2 − 2as = u 2
u = v 2 − 2as
Make l the subject of A = πr (l + r )
A
=l+r
A = πrl + πr 2 or
πr
A
−r =l
A − πr 2 = πrl
πr
A − πr 2
A
l=
l=
−r
πr
πr
© Nuffield Foundation 2004
Divide by v to leave t on its own.
There is only one term in the formula with s in it (2as).
Subtract u2 from both sides to isolate the term 2as.
Divide (the whole of) both sides by 2a to leave s on its own
and write with s at the left hand side.
There is only one term in the formula with u in it (u2)
Subtract 2as from both sides to leave only the term
involving u on one side of the formula.
Take the square root to give the formula for u.
There is more than one method:
Remove the bracket
or
Divide by the term outside
Isolate the term with l
Write with l at the left hand side.
AS Use of Maths Scheme of Work Wizard Nelson Thornes Ltd
AS: Use of Maths
Algebra & Graphs
Practice sheet
Examples
Method
Make m the subject of:
1
E = mv 2 + mgh
2
2 E = mv 2 + 2 mgh
2 E = m(v 2 + 2 gh )
2E
m= 2
v + 2 gh
Multiply every term by 2 to get rid of the fraction.
Write m outside a bracket as a common factor.
Divide by the bracket to leave m on its own.
Some to try
1
Make I the subject of V = IR
2
Make m the subject of y = mx + c
3
Make h the subject of V = πr 2 h
4
Make r the subject of V = πr 2 h
5
Make u the subject of v = u + at
6
7
Make W the subject of P = 2(L + W )
8
9
Make h the subject of A =
h(a + b)
2
10
Make P the subject of I =
PRT
100
Make l the subject of L = l (1 + αt )
Make a the subject of A =
h(a + b)
2
11
Make m the subject of I = mv − mu
12
Make u the subject of I = mv − mu
13
Make h the subject of A = 2πr 2 + 2πrh
14
Make a the subject of s = ut + 12 at 2
16
Make v the subject of E = 12 cv 2
18
Make C the subject of F = 95 C + 32
15
17
Make d the subject of F =
Make T the subject of c =
L
4πd 2
T
µ
19
Make r the subject of A = π (R 2 − r 2 )
20
21
Make p the subject of E 2 = p 2 c 2 + m 2 c 4
22
23
Make v the subject of E =
© Nuffield Foundation 2004
mc 2
v2
1− 2
c
24
Make l the subject of T = 2π
Make R the subject of
l
g
1
1
1
=
+
R R1 R2
Make v the subject of p =
mv
1−
v2
c2
AS Use of Maths Scheme of Work Wizard Nelson Thornes Ltd
AS: Use of Maths
Algebra & Graphs
Practice sheet
Answers
Other answers are possible – if in doubt, ask your tutor.
1
4
7
10
13
16
19
22
I=
V
R
2
r=
V
πh
5
W =
P
P − 2L
− L or
2
2
8
a=
2A
2 A − hb
− b or
h
h
11
h=
A − 2πr 2
2πr
14
y−c
x
3
u = v − at
6
L
1 + αt
9
m=
l=
m=
a=
2E
c
17
T = µc 2
r=
πR 2 − A
π
20
 T 
l =
 g
 2π 
R1 R2
R1 + R2
© Nuffield Foundation 2004
23
15
2( s − ut )
t2
v=
R=
12
I
v−u
18
21
2
 mc 2
v = c 1 − 
 E




2
24
h=
V
πr 2
P=
100 I
RT
h=
2A
a+b
u=
mv − I
m
d=
L
4πF
C=
p=
v=
5
9
(F − 32)
E 2 − m2 c 4
c2
1
m
1
+ 2
2
p
c
2
AS Use of Maths Scheme of Work Wizard Nelson Thornes Ltd
AS: Use of Maths
Algebra & Graphs
Practice sheet
Extra practice
Make x the subject of the following:
1
3x + 1 = y
2
12 − 2 x = 4 y + 2
3
4
3 + 4 y + 2x = 9
5
2 xy + 1 = 3 y
6
2( x + 3) = 3( x + 2 y − 1)
7
x −1
=3
y+2
8
2
x +1
9
3− x
=x
y
xy
=3
x +1
12
3b
x
15
x−z x+ y
=
2
3
18
10
3
= 5y
x −1
11
13
z = x2 y + 3
14
16
y = (2 x + 3)
17
y=
xyz =
y=
x +1
2
y −3=
x
2x + 1
( x + 1) 2 = 3ab + 1
y=
1
x
19
z2 = x2 + y2
20
2( x + 3) − 3( y + 2) = 4 xy
21
z = xy + 1
22
x
n
= 2
y +1 x y
23
x + 3y
=3
z − 2x
24
( x − 1) 2
+ (2 y + 1) 2 = 1
4
© Nuffield Foundation 2004
AS Use of Maths Scheme of Work Wizard Nelson Thornes Ltd
AS: Use of Maths
Algebra & Graphs
Practice sheet
Answers
1
2
4
y −1
3
x = 3 − 2y
7
x = 3y + 7
8
x=
3
+1
5y
11
x=
z −3
y
14
x=
y2 − 3
2
17
10
13
16
19
22
x=
x = z2 − y2
x=3
n( y + 1)
y
© Nuffield Foundation 2004
5
20
23
x = 5 − 2y
3
x = 2y −1
3y − 1
2y
6
x = 9 − 6y
2
−1
y
3
x=
y−3
9
x=
x=
3b
yz
x = 2 y + 3z
x=
12
15
18
x=
3y
2 − 4y
21
x=
3( z − y )
7
24
3
y +1
3− y
x=
2y − 7
x=
x = (3ab + 1) − 1
x=
x=
1
y2
(z − 1)2
y
x = 2 1 − (2 y + 1) 2 + 1
AS Use of Maths Scheme of Work Wizard Nelson Thornes Ltd