1. finance
2. investing
3. day trading

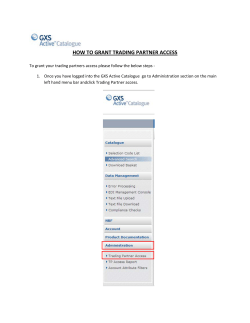
Journal of Banking & Finance 36 (2012) 575–583
Contents lists available at SciVerse ScienceDirect
Journal of Banking & Finance
journal homepage: www.elsevier.com/locate/jbf
A unique ‘‘T + 1 trading rule’’ in China: Theory and evidence
Ming Guo a,⇑, Zhan Li b, Zhiyong Tu c
a
Shanghai Institute of Advanced Finance, Shanghai Jiaotong University, Shanghai, China
Department of Economics, W.P. Carey School of Business, Arizona State University, USA
c
HSBC School of Business, Peking University, Shenzhen, China
b
a r t i c l e
i n f o
Article history:
Received 6 July 2009
Accepted 3 September 2011
Available online 10 September 2011
JEL classification:
G11
G12
a b s t r a c t
Unique to the world, China adopts a ‘‘T + 1 trading rule’’, which prevents investors from selling stocks
bought on the same day. We develop a dynamic price manipulation model to study the effects of the
‘‘T + 1 trading rule’’. Compared to the ‘‘T + 0 trading rule’’, which allows investors to buy and sell the same
stocks during the same day, we show that the ‘‘T + 1 trading rule’’ reduces the total trading volume and
price volatility, and improves the trend chasers’ welfare when trend-chasing is strong. An empirical test
using data on China’s B-share stock market supports the model’s theoretical predictions.
Ó 2011 Elsevier B.V. All rights reserved.
Keywords:
T + 1 trading rule
Trading volume
Volatility
Trend-chasing
1. Introduction
The Chinese stock market opened in December 1990, with two
separate sub-markets: an A-share market (for domestic investors)
and a B-share market (for foreign investors). Initially, both adopted
the ‘‘T + 0 trading rule’’, which allows an investor to sell stocks
bought the same day. However, in January 1995, the China Securities Regulatory Commission (CSRC) abandoned this ‘‘T + 0 trading
rule’’ for A-share stocks and replaced it with a ‘‘T + 1 trading rule’’
– a unique institutional arrangement found nowhere else in the
world. The ‘‘T + 1 trading rule’’ requires an investor to sell only
stocks he purchased at least one day prior, and forbids him from
selling stocks bought the same day. In China’s official newspaper,
Renmin Daily, the authority claimed that the ‘‘T + 1 trading rule’’
would effectively prevent excessive speculative trading and thus
would be in line with the interests of retail investors.1 In 2000, China’s B-share stock market abandoned the ‘‘T + 0 trading rule’’, and
adopted the ‘‘T + 1 trading rule’’ as well. Despite the longstanding
arguments in favor of the ‘‘T + 1 trading rule’’, few theoretical models
and little empirical evidence have been provided to explain and analyze this unique trading arrangement. Our paper may be the first to
explore the effects of the ‘‘T + 1 trading rule’’ on the welfare of
various investors, the stock prices, and volumes, from both theoretical and empirical perspectives.
We develop a parsimonious trade-based price manipulation
model in which there are three types of traders: a strategic trader,
mechanical trend chasers, and competitive risk-averse liquidity
providers. The risk-averse liquidity providers passively clear the
market by taking orders submitted by the strategic trader and
trend chasers. The strategic trader maximizes her expected utility
by manipulating the stock prices to induce trend chasers to follow
her trading, whereas the trend chasers follow a pre-specified trading rule.2 The stock price is affected by the strategic trader’s manipulation trades as well as by the trend chasers’ trend-following
behavior. We show that, compared with the ‘‘T + 0 trading rule’’,
adopting the ‘‘T + 1 trading rule’’ effectively reduces the total trading
volume, as well as price volatility, and improves the trend chasers’
welfare if trend-chasing is strong. We test the model’s predictions
by comparing trading volume and stock price volatility before and
after the implementation of ‘‘T + 1’’, using data from China’s B-share
market. We also check the robustness of our test by examining different measures of stock volatility and by controlling the effect of
the ‘‘Opening-up’’ policy, which was introduced about the same time
as the introduction of the ‘‘T + 1 trading rule’’. The empirical results
support our hypotheses.
⇑ Corresponding author. Tel.: +86 21 62932017; fax: +86 21 62933418.
E-mail addresses: [email protected], [email protected] (M. Guo), zhan.li@
asu.edu (Z. Li), [email protected] (Z. Tu).
1
Due to the lack of rigorous regulation in the early 1990s, China’s stock market is
dominated by speculative trading, as in most emerging markets.
0378-4266/$ - see front matter Ó 2011 Elsevier B.V. All rights reserved.
doi:10.1016/j.jbankfin.2011.09.002
2
Trend-following behavior is common in emerging markets, see Gelos and Wei
(2002) and Khwaja and Mian (2005). It is very common among retail investors in
China as well.
576
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
Our paper is closely related to the literature on stock market
manipulation. Allen and Gale (1992) classify stock market manipulation into three categories: action-based manipulation, information-based manipulation, and trade-based manipulation. Our
theory falls into the trade-based manipulation category, in which
a trader manipulates a stock simply by buying and selling, without
taking any publicly-observable action to change the firm’s value, or
releasing any information to affect the price. Hart (1977) shows, in
a dynamic deterministic setting, that trade-based manipulation is
profitable when the stationary equilibrium is unstable or demand
functions are nonlinear. Jarrow (1992) extends Hart (1977) to a
stochastic environment and shows that the manipulation can be
profitable if there exists a ‘‘price momentum’’, or when the speculator can corner the market. In these papers, the demand functions
are exogenously given and their frameworks are thus of partial
equilibria.3 We take a general equilibrium approach here. In our paper, there exist risk-averse liquidity providers who clear the markets
so that the demand function is endogenously determined. In addition, we assume there exist trend chasers, who follow an exogenously-given trading rule. The rule requires them to buy stocks
when the price goes up and sell stocks when the price goes down.
DeLong et al. (1990) classifies this type of trading as positive feedback
trading. They cite various empirical evidence to support this assumption. Our model is similar to DeLong et al. (1990) in that we also assume the rational strategic trader can manipulate the positive
feedback trader to make a profit. However, our paper differs from
theirs in two aspects. First, our model assumes information symmetry among traders because we focus on the effects of the ‘‘T + 1 trading rule’’. In contrast, DeLong et al. (1990) assume information
asymmetry among different types of traders, aiming primarily at
manipulative behavior. Second, in their paper, the equilibrium price
is obtained by directly specifying demand functions for passive traders, while in our model, the demand of the passive traders, or, riskaverse liquidity providers, is determined by their own utility maximization, following Subrahmanyam (1991).
Several papers document empirical evidence of market manipulation for both emerging and developed markets. Using trade-level data from Pakistan stock market, Khwaja and Mian (2005) find
that brokers earn at least 8% higher returns on their own trades
through a specific trade-based ‘‘pump and dump’’ price manipulation scheme. Mei et al. (2004) empirically test a price manipulation
pattern based on investors’ behavioral biases, using data on Securities and Exchange Commission (SEC) prosecution of ‘‘pump and
dump’’ manipulation cases. Aggarwal and Wu (2006) also provide
empirical evidence from 142 litigation cases of stock price manipulation in the U.S. from 1990 to 2001.
The rest of this paper is organized as follows. Section 2 specifies
the assumptions of the model. Section 3 solves the equilibrium for
the case of the ‘‘T + 1 trading rule’’. Section 4 solves the equilibrium
for the case of the ‘‘T + 0 trading rule’’. In Section 5, we compare the
equilibrium features of these two cases with regard to trading volume, price volatility, and investors’ welfare. Section 6 tests for the
predictions in Section 5, using data from China’s B-share market.
Section 7 concludes the paper.
2. The model
For tractability, we consider a two-day model in which there are
three types of traders: a risk-averse strategic trader, trend chasers,
and risk-averse liquidity providers. There are one risk-free bond
and one risky stock available for trading. Without loss of generality, we assume that the interest rate for the bond is zero. Therefore,
the bond’s price is always equal to 1.
3
See also Merrick et al. (2005) and Vitale (2000).
The model involves two days, in which day 1 comprises periods
1–4, and the stock payoff is realized and the stock is liquidated in
day 2.4 Before period 1, the strategic trader and the risk-averse
liquidity providers know that the stock’s payoff is D0. Uncertainty
about the stock’s payoff arises in period 1 and ends in the second
day. From periods 1 to 4, the strategic trader and the risk-averse
liquidity providers know only that the stock payoff D follows a normal distribution with a mean D0 and a variance r2. The uncertainty
is resolved in day 2 and the stock payoff D is realized.
The strategic trader chooses her optimal trading strategy, while
trend chasers follow an exogenously-given rule. Risk-averse liquidity providers trade passively to provide immediacy to other investors for liquidity premium, and set equilibrium prices
competitively based on the order flows submitted by the strategic
trader and trend chasers.5 Note that because there is no information
asymmetry, it does not make any difference to risk-averse liquidity
providers whether they observe the order flows separately or in
total.
Since the liquidity providers are risk averse, the order flows
submitted by the strategic trader and trend chasers affect the stock
prices in equilibrium. As a result, the strategic trader chooses her
optimal trading strategies by taking into account the impact of
her trades on prices. The strategic trader has an exponential utility
of the form exp (cW), where c is her risk-aversion coefficient.
We also assume an exponential utility exp (cW) for risk-averse
liquidity providers. Without loss of generality, we normalize the
number of risk-averse liquidity providers to be 1. The stock price
in period i is denoted by Pi, where i 2 {1, 2, 3, 4, 5}. Since there is
no uncertainty in period 5 (day 2), the price in period 5 satisfies
that P5 = D. Since there is no uncertainty before period 1, the stock
price before period 1 is equal to D0.
We assume that the strategic trader’s initial stock endowment
is X0, where X0 is a positive constant. The initial endowments of
risk-averse liquidity providers are assumed to be zero and their
holding in period i, where i 2 {1, 2, 3, 4}, is denoted by Qi.
For simplicity, we assume that the strategic trader trades in
periods 1 and 3, and the quantities she trades are denoted by X
and X, respectively. The trend chasers follow the strategic trader’s
trading and trade in periods 2 and 4. The quantities chosen by
them in these two periods are denoted by Y and Y, respectively.
They are given by the following rule:
Y ¼ gðP1 D0 Þ;
ð1Þ
and
Y ¼ gðP3 P2 Þ;
ð2Þ
where g is a positive constant. As in DeLong et al. (1990), g represents the intensity of the bullishness of trend chasers.
We now introduce the ‘‘T + 1 trading rule’’ into the model. Under the ‘‘T + 1 trading rule’’, the quantities an investor sells in day
1 cannot be more than his initial position at the beginning of day
1. This rules out the case where an investor buys a large number
of stocks and sells this quantity during the same day.
4
In essence, we only focus on the intra-day trading behaviors of the investors, to
study the effect of the ‘‘T + 1 trading rule’’. However, our results should be robust in a
more complicated setup.
5
It is worth noting that individual investors also provide liquidity in other markets,
as empirical evidence has indicated. Kaniel et al. (2008, 2009) have shown that riskaverse individual investors provide liquidity to institutional investors in the U.S.
Therefore, it is reasonable to assume that the risk-averse liquidity providers
(individual investors) clear the market at the equilibrium price. Technically, many
papers assume exogenous demand functions of risk-averse liquidity providers, for
tractability reasons. For example, Brunnermeier and Pedersen (2005) incorporate the
price impacts of order flows and downward-sloping demands of risk-averse liquidity
providers into asset pricing models. In their paper, the demand curve is exogenously
given. Our paper, on the other hand, endogenizes the demands of the liquidity
providers when incorporating the price impacts of order flows.
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
577
In this section, we solve for the equilibrium under the ‘‘T + 1
trading rule’’.
where X is the quantity she trades in period 3 and X0 is her initial
position.
Simple derivation yields the strategic trader’s budget constraint
in period 3:
3.1. Equilibrium prices
W 5 W 2 ¼ ðX 0 þ XÞðP5 P2 Þ þ XðP5 P3 Þ:
Since the risk-averse liquidity providers’ goal is to clear the
markets in each period, the sum of the positions of the strategic
trader, trend chasers, and risk-averse liquidity providers must be
equal to zero. We thus obtain
Her maximization problem in period 3 is then given by6:
0 ¼ Q 1 þ X;
s:t: ðaÞ W 5 W 2 ¼ ðX 0 þ XÞðP 5 P2 Þ þ XðP5 P3 Þ
3. Equilibrium under the ‘‘T + 1 trading rule’’
0 ¼ Q 2 Q 1 þ Y;
0 ¼ Q 4 Q 3 þ Y:
The risk-averse liquidity providers set prices competitively to clear
the market. Following Subrahmanyam (1991), the quantities traded
by risk-averse liquidity providers satisfy:
1
E½Q t ðD Pt Þ cVar½Q t ðD Pt Þ ¼ 0:
2
ð4Þ
With the above equation, we establish the relationship between the
equilibrium prices and the risk-averse liquidity providers’ holdings,
in the following proposition.
Proposition
1. The
stock
P t ¼ D0 12 cr2 Q t ; t ¼ f1; 2; 3; 4g.
c
max EðW 5 jF 3 Þ VarðW 5 jF 3 Þ
2
X
price
in
period
t
is
ð10Þ
ðbÞ X P X 0 ;
ð3Þ
0 ¼ Q 3 Q 2 þ X;
ð9Þ
where F 3 denotes her information set in period 3. Since her objective function is quadratic, we need only to solve the optimization
problem in (10) without constraint (b) and then determine whether
the solution is larger than X0.
The optimization problem without constraint (b) is given by
c
max EðW 5 jF 3 Þ VarðW 5 jF 3 Þ
2
X
ð11Þ
s:t: ðaÞ W 5 W 2 ¼ ðX 0 þ XÞðP 5 P2 Þ þ XðP5 P3 Þ:
Substituting (5), (1), and constraint (a) into the objective function in
(11) yields:
max W 2 kðX 0 þ XÞð1 þ gkÞX kXðX þ gkX þ XÞ kðX 0 þ X þ XÞ2 :
X
Proof. Since D N(D0, r2), substituting E[Qt(D Pt)] = Qt(D0 Pt)
and 12 cVar½Q t ðD Pt Þ ¼ 12 cQ 2t r2 into (4) yields Pt ¼ D0 12 cr2 Q t ;
t ¼ f1; 2; 3; 4g. h
Define k ¼ 12 cr2 . Using equations (3) and Proposition 1, we
obtain
P1 ¼ D0 þ kX;
P2 ¼ D0 þ kðX þ YÞ;
P3 ¼ D0 þ kðX þ Y þ XÞ;
ð5Þ
P4 ¼ D0 þ kðX þ Y þ X þ YÞ:
Substituting (5) into (1) and (2) yields the quantities traded by
trend chasers in periods 2 and 4, which are given by
Y ¼ gðP1 D0 Þ ¼ gkX
ð6Þ
and
Y ¼ gðP3 P2 Þ ¼ gkX:
ð7Þ
3.2. The strategic trader’s optimization problem
In day 1 (periods 1–4), the strategic trader trades in periods 1
and 3 to maximize her expected utility in day 2 (period 5). We
use the backward induction method to solve for her optimal trading strategies. We first solve the optimization problem of the strategic trader in period 3 and then solve for her optimal trading in
period 1.
3.2.1. The maximization problem in period 3
In period 3, the strategic trader maximizes her expected utility
in period 5 based on the information available in period 3. With the
‘‘T + 1 trading rule’’, the quantity that the strategic trader sells cannot be more than X0. Therefore, we have the following constraint:
X P X 0 ;
ð8Þ
ð12Þ
The first-order condition (FOC) gives:
1
ðgk þ 3ÞX
:
X0 ¼ X0 2
4
ð13Þ
It is easy to check that the second-order condition is negative. Thus,
the solution (13) is the optimal one. If X 0 P X 0 , then (13) is also
the solution to the constrained optimization problem given by
(10). If X 0 < X 0 , because the objective function is quadratic and
concave, the constraint will be binding at X0. Therefore, combining
the above two cases, we can write the optimal solution to problem
(10) as:
X ¼ maxfX 0 ; X 0 g:
ð14Þ
Eq. (14) shows that the strategic trader’s optimal strategy in period
3 is a nonlinear function of her initial endowment X0 and her chosen
quantity X in period 1. Eq. (13) shows that X 0 is negatively correlated with X. The implication is that the strategic trader tends to
trade in the opposite directions in periods 1 and 3 to manipulate
markets and obtain trading profit by inducing trend chasers to follow her transaction. An example is that she buys low and sells high.
Note that X 0 is also negatively correlated with her initial endowment X0, because the risk-averse strategic trader tends to hold a position with a smaller magnitude to reduce the risk. In addition, Eq.
(14) shows that the quantities she sells in period 3 are up-bounded,
which is consistent with the ‘‘T + 1 trading rule’’.
3.2.2. The maximization problem in period 1
In period 1, the strategic trader’s budget constraint is given by
W 5 W 0 ¼ X 0 ðP5 D0 Þ þ XðP5 P 1 Þ þ XðP 5 P3 Þ;
ð15Þ
and her optimization problem is:
6
Given u(W) = exp (cW), max E[u(W)] is equivalent to max EðWÞ 12 cVarðWÞ .
578
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
c
jXj 6 kX 0 ; k > 0:
max EðW 5 jF 1 Þ VarðW 5 jF 1 Þ
X
2
s:t: ða0 Þ W 5 W 0 ¼ X 0 ðP5 D0 Þ þ XðP5 P1 Þ þ XðP5 P3 Þ
0
ðb Þ X P X 0 ;
ð16Þ
where F 1 is the strategic trader’s information set in period 1.
Substituting constraint (a0 ), (1) and (5) into her objective function
(16) yields:
max
X
2
X XðX þ gkX þ XÞ ðX 0 þ X þ XÞ
2
0
ð17Þ
s:t: ðb Þ X P X 0 :
Given X ¼ maxfX 0 ; X 0 g, we solve the optimization problem given
in (17) by considering X 0 P X 0 and X 0 < X 0 , respectively. We
summarize the results in the following proposition.
Proposition 2. Under the ‘‘T + 1 trading rule’’, when gk > 1, the
strategic trader has two optimal trading strategies. The first one is:
X ¼ gk 4þ 1 X 0 and X ¼ X 0 . The second one is: X⁄ = X0 and
X ¼ gk 4þ 1 X 0 . When 0 < gk < 1, the strategic trader has a unique
optimal trading strategy, i.e., X ¼ X ¼ gk2Xþ0 7.
Proof. See Appendix A. h
Proposition 2 shows that the strategic trader’s optimal trading
strategy depends crucially on gk, the strength of the trend-following
behavior. The larger gk is, the more manipulation profit the strategic
trader can obtain. When gk > 1, the profit from market manipulation
dominates the inventory risk she takes, therefore the optimal trading in periods 1 and 3 shall go in opposite directions. Since the model
structure is symmetric, buying in the first period and selling in the
third one shall yield the same utility as selling in the first period
and buying in the third one. However, when gk < 1, market manipulation profit is relatively low, so reducing the risk of stock-holding
becomes the dominant consideration. Then the strategic trader
tends to reduce her inventory in both periods 1 and 3.
4. Equilibrium under the ‘‘T + 0 trading rule’’
In a market adopting the ‘‘T + 0 trading rule’’, an investor can
sell stocks she purchases during the same day. In this section, we
solve for the strategic trader’s optimal strategies in this institutional arrangement. Compared with the previous section, the only
difference is that she solves her maximization problem without the
constraint X P X 0 . We solve the strategic trader’s optimal trading
quantities X⁄ and X by backward induction, as in the previous section. In period 3, the strategic trader maximizes her expected utility in period 5, given the quantity X she trades in period 1. The
solution is equal to X 0 , derived in the previous section, that is,
1
ðgk þ 3ÞX
:
X ¼ X0 2
4
ð18Þ
The strategic trader’s maximization problem in period 1 is given by
1
1
1
1
X 0 gk X 0 X X 20 :
max ðgk þ 7Þðgk 1ÞX 2 þ
X
8
2
2
2
2
X0:
gk þ 7
The above constraint means that the quantity the strategic trader
buys or sells cannot be more than kX0 in the first period. It is a
mechanical assumption to obtain an interior solution. We further
assume that k P 1, and k can be understood as an investor’s funding
ability.7 Comparing the utilities from X = kX0 and X = kX0, we find
that the objective function (19) is maximized at the right boundary:
X ¼ kX 0 :
ð22Þ
Substituting (22) into Eq. (18), the strategic trader’s optimal trading
0
quantity in period 3 is given by X ¼ 12 X 0 ðgkþ3ÞkX
. We summarize
4
the above results in the following proposition.
Proposition 3. Under the ‘‘T + 0 trading rule’’, when gk > 1, the
strategic trader’s optimal trading quantities are: X⁄ = kX0 and
0
X ¼ 12 X 0 ðgkþ3ÞkX
. When 0 < gk < 1, the strategic trader’s optimal
4
2
trading quantities are: X ¼ X ¼ gkþ7
X0.
The interpretation of the optimal trading strategies in Proposition 3 is the same as in Proposition 2, except that the solution is
unique when gk > 1. This is due to the fact that we impose a bound
for the first-period trading under the ‘‘T + 0’’ scenario, which makes
the model asymmetric.
5. Comparison of ‘‘T + 1’’ and ‘‘T + 0’’ trading rules
In this section, we compare the equilibrium properties for these
two trading mechanisms. First, in Table 1, we summarize the strategic trader’s optimal trading strategies, described in the previous
two sections.
Next, we compare the equilibrium properties, including total
trading volumes, price volatilities, and investors’ welfare.
5.1. Equilibrium volumes
We use V(T+1) and V(T+0) to denote total trading volumes under
the ‘‘T + 1’’ and ‘‘T + 0’’ trading rules, respectively.
Under the ‘‘T + 1 trading rule’’:
V ðTþ1Þ ¼ jX j þ jY j þ jX j þ jY j
gk þ 1
gkðgk þ 1Þ
X0 þ
X 0 þ X 0 þ gkX 0
4
4
g 2 k2 þ 6gk þ 5
X0:
¼
4
¼
Under the ‘‘T + 0 trading rule’’:
V ðTþ0Þ ¼ jX j þ jY j þ jX j þ jY j
1
ðgk þ 3ÞkX 0
X0 þ
¼ kX 0 þ gkkX 0 þ
ðgk þ 1Þ
2
4
1
¼ ðkðgk þ 7Þ þ 2Þðgk þ 1ÞX 0 :
4
Comparing V(T+1) with V(T+0) yields:
1 2 2
7
3
X0 :
g k ðk 1Þ þ gkð2k 1Þ þ k 4
4
4
ð19Þ
V ðTþ0Þ V ðTþ1Þ ¼
ð20Þ
It is easy to note that when k > gkþ3
; V Tþ0 V Tþ1 > 0. Since k P 1,
gkþ7
adopting the ‘‘T + 1 trading rule’’ tends to reduce the total trading
volume. Intuitively, the ‘‘T + 1 trading rule’’ imposes an upper-limit
for the strategic trader to manipulate the price, thus inducing less
trading.
When gk < 1, the first-order condition yields
X ¼ ð21Þ
The second-order condition is 18 ðgk þ 7Þðgk 1Þ < 0. Substituting
2
(20) into (18), we obtain X ¼ gkþ7
X0 .
When gk > 1, the objective function (19) is convex; it is maximized at either 1 or +1. In order to ensure a bounded solution,
we make the following assumption:
7
This assumption is for tractability reasons. However, we think it is also
reasonable, since an investor is likely to obtain a loan of the same dollar value, using
her initial stock holding X0 as collateral.
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
Table 1
The strategic trader’s optimal trading strategies under ‘‘T + 1’’ and ‘‘T + 0’’ trading
rules.
gk > 1
X
ðg 2 k2 þ 2gk 7ÞX 20
8
kðgk 1Þðkgk þ 7k þ 4Þ 4 2
X0
8
1
¼ ðgk 1Þðk þ 1Þðkgk þ 7k gk 3ÞX 20 :
8
U ðTþ1Þ U ðTþ0Þ ¼
0 < gk < 1
⁄
X
T+1
gkþ1
4 X 0 ðor
T+0
kX0
X0 Þ
X 0
12 X 0
or
gkþ1
4 X0
ðgkþ3ÞkX 0
4
X⁄
X
2
gkþ7
X0
2
gkþ7
X0
2
gkþ7
X0
2
gkþ7
X0
579
When k P 1, we have:
U Tþ1 < U Tþ0 :
5.2. Price volatilities
We use Pmax Pmin to measure the price volatility, where Pmax
and Pmin are the maximum and minimum prices in day 1,
respectively.8
Under the ‘‘T + 1 trading rule’’, the strategic trader has two equilibrium trading strategies. It is easy to check that these two strategies actually yield the same price volatility measured by
Pmax Pmin. Without loss of generality, we consider only the case
where gk > 1.9 Under this scenario, the price rises in periods 1 and
2 and falls in periods 3 and 4. The maximum price must be P2 and
2
the minimum price can be D0 or P4. We have P 2 ¼ D0 þ k ðgkþ1Þ
X0
4
g 2 k2 2gk3
and P4 ¼ D0 þ k
X
.
0
4
When gk > 3, P4 > D0, min{D0, P4} = D0,
rðTþ1Þ
ðgk þ 1Þ2
¼ jP2 D0 j ¼ k
X0 :
4
When gk < 3, we have P4 < D0, min{D0, P4} = P4,
rðTþ1Þ ¼ jP2 P4 j ¼ kX 0 ð1 þ gkÞ:
Under the ‘‘T +0 trading rule’’, P2 ¼ D0 þ kðgk þ 1ÞkX 0 ; P 4 ¼
D0 þ k 12 þ 1gk
k ð1 þ gkÞX 0 < D0 , so the price volatility is:
4
rðTþ0Þ
1 1 gk
k ð1 þ gkÞX 0
¼ jP2 P4 j ¼ kðgk þ 1ÞkX 0 k þ
2
4
1 gk þ 3
þ
k ð1 þ gkÞX 0 :
¼k
2
4
Simple calculation yields that:
when gk > 3,
1
4
rðTþ0Þ rðTþ1Þ ¼ kðgk þ 1Þðkgk gk þ 3k þ 1ÞÞX 0 > 0;
and, when gk < 3,
1
4
rðTþ0Þ rðTþ1Þ ¼ kðgk þ 1Þðkgk 2 þ 3kÞX 0 > 0:
Therefore, we find that the ‘‘T + 1 trading rule’’ reduces the price
volatility relative to the ‘‘T + 0’’ rule when the strength of trend-following is strong.
5.3. Welfare
In this section, we compare both the strategic trader and trend
chasers’ welfare under two trading rules. Given the results presented in Tables 1 and A.1 in Appendix A, it is easy to see that when
0 < gk < 1 the strategic trader’s expected utilities under the two
scenarios are the same. We next consider the case that gk > 1,
where
8
The volatility measurement with high price minus low price has been widely used
by financial professionals. It is also explored in the academic literature, e.g., Garman
and Klass (1980).
9
When gk < 1, these two mechanisms have the same price volatility, based on
Table 1.
Thus the strategic trader is better off under the ‘‘T + 0 trading rule’’
when k P 1. Intuitively, the strategic trader can manipulate prices
to a larger extent without constraints on the maximum quantities
she can sell.
With regard to trend chasers, we measure their welfare by their
expected trading profit. Under the ‘‘T + 1 trading rule’’, the trend
chasers’ welfare is given by:
ðgk þ 1Þgk
X 0 þ ðP4 D0 ÞgkX 0
4
ðgk þ 1Þ2 ðgk þ 1Þgk
g 2 k2 2gk 3
¼ k
X0 þ k
X 0 gkX 0
X0
4
4
4
1
¼ gkð1 þ gkÞðg 2 k2 2gk þ 13ÞkX 20 :
16
W ðTþ1Þ ¼ EðD P2 Þ
Under the ‘‘T + 0 trading rule’’, the trend chasers’ welfare is given
by:
1
ðgk þ 3ÞkX 0
W ðTþ0Þ ¼ ðD0 P2 ÞgkkX 0 þ ðP 4 D0 Þ X 0 þ
gk
2
4
1
2
2
2
¼ gk2 ð1 þ gkÞðg 2 k2 k þ 4kgk þ 2gkk þ 4k þ 13k þ 4ÞX 20 :
16
The difference between trend chasers’ welfare under the ‘‘T + 1’’ and
‘‘T + 0’’ mechanisms is given by:
1 2 2
k gX 0 ðk þ 1Þð1 þ gkÞðg 2 k2 k g 2 k2
16
þ 2kgk þ 2gk þ 13k 9Þ < 0:
W ðTþ0Þ W ðTþ1Þ ¼ This shows that trend chasers are better off under the ‘‘T + 1 trading
rule’’. In summary, we show that compared with the ‘‘T + 0 trading
rule’’, adopting the ‘‘T + 1 trading rule’’ reduces the total trading volume and the price volatility, and protects the welfare of trend chasers. Intuitively, the ‘‘T + 1 trading rule’’ imposes an upper-bound on
the magnitude to which the strategic trader can manipulate prices.
As a result, total trading volume, as well as price volatility, decreases and trend chasers benefit from a smaller amount of negative
profit from trading under ‘‘T + 1’’. The results are summarized in the
following proposition.
Proposition 4. Compared with the ‘‘T + 0 trading rule’’, the ‘‘T + 1
trading rule’’ leads to smaller total trading volume, lower price
volatility, and higher welfare for trend chasers.
6. Empirical test
In this section, we test the model’s predictions that, when
trend-chasing is strong, introducing the ‘‘T + 1 trading rule’’ will reduce both price volatility and total trading volume. In China’s stock
market, price manipulation and trend-chasing behavior are very
common. Therefore, we expect that the above hypothesis holds.
The Chinese stock market is separated into an A-share market
and a B-share market. In the A-share market, listed stocks are
traded in Chinese currency RMB, while all stock transactions listed
in the B-share market are carried out in foreign currencies. The Ashare market was introduced in December, 1990 and included only
eight stocks. The B-share market was introduced in February 1992.
580
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
Initially, both markets adopted the ‘‘T + 0 trading rule’’. In January
1995, however, the A-share market abandoned the ‘‘T + 0 trading
rule’’ and replaced it with the ‘‘T + 1 trading rule’’. The B-share market adopted the ‘‘T + 1 trading rule’’ in December 2001. We test the
predictions in Proposition 4 with data from the B-share market. We
understand that we can obtain richer data from the A-share market, but that market switched its trading rule at a time when the
Chinese stock market was still quite immature and we are concerned with the quality of the data, so we believe that using data
from the B-share market could be the better choice.
For comparison, we include two years of data before and after
the switch from the ‘‘T + 0 trading rule’’ to the ‘‘T + 1 trading rule’’,
to test our hypotheses. More specifically, our sample consists of
daily data of 109 B-share stocks listed on China’s B-share market
from December 1999 to November 2003. There are 955 trading
days included: 479 trading days are under the ‘‘T + 0 trading rule’’
and 476 trading days are under the ‘‘T + 1 trading rule’’. We use i to
denote the stock, i 2 [1, 109], and t to denote the trading day,
t 2 [1,955]. Let Vi,t denote the daily volume of stocki in the number
P
of shares at day t. Following our theory, we use ln Pi;t;h as a meai;t;l
sure of daily price volatility of stock i in day t, where Pi,t,h and Pi,t,l
are the highest and lowest prices of stock i on day t, respectively.
Under the ‘‘T + 0 trading rule’’, the average daily trading volume
and price volatility for stock i are given by:
V ðTþ0Þi ¼
479
1 X
V i;t and
479 t¼1
rhighlow
¼
ðTþ0Þi
479
1 X
rhighlow ;
479 t¼1 i;t
where rhighlow
is stock i’s volatility on day t, which denotes volatili;t
ity calculated from Pi,t,h and Pi,t,l. Similarly, under the ‘‘T + 1 trading
rule’’, the average daily trading volume and price volatility for stock
i are:
V ðTþ1Þi ¼
955
1 X
V i;t and
476 t¼480
rhighlow
¼
ðTþ1Þi
955
1 X
rhighlow :
476 t¼480 i;t
For robustness, we also use the standard deviation of close-toclose log return series for each stock, to measure the stock’s volaP close;t
tility. The return series r i;t ¼ ln P
close;t1
, where Pclose,t and Pclose,t1 are
stock i’s close prices on day t and day t 1, respectively. The volatility under the ‘‘T + 0 trading rule’’ is defined by the sample stanqffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ffi
P479
1
2
dard deviation of the return series: rstd
t¼1 ðr i;t r i Þ ,
ðTþ0Þi ¼
4791
where ri is the average of the return series. The volatility under
the ‘‘T + 1 trading rule’’ can be defined in a similar way and we denote it as rstd
ðTþ1Þi .
Denote the differences in trading volume and price volatilities
due
to
the
change
of
trading
rule
by
DV i ¼
¼ rhighlow
rhighlow
V ðTþ0Þi V ðTþ1Þi ; Drhighlow
i
ðTþ0Þi
ðTþ1Þi
and
Drstd
¼
i
std
rstd
ðTþ0Þi rðTþ1Þi respectively. Table 2 presents the summary statistics of DV i ; Drhighlow
and Drstd
for 109 B-share stocks.
i
i
Table 2
Summary statistics of 109 B-share stocks’ DV i ; Drhighlow
and Drstd
i .
i
DVi/shares
Drhigh—low
i
Drstd
i
Mean
Std. dev.
Skewness
Kurtosis
1,076,723
1,062,113
0.6487
6.2444
0.0171
0.0038
0.4847
3.8327
0.0130
0.0093
7.0493
67.7707
Min
5% Qntl.
25% Qntl.
50% Qntl.
75% Qntl.
95% Qntl.
Max
2,701,784
111,190
462,714
871,991
1,521,220
3,224,088
5,254,964
0.0045
0.0105
0.0146
0.0177
0.0194
0.0222
0.0268
0.0732
0.0065
0.0108
0.0108
0.0165
0.0186
0.0381
Table 2 shows that the average volume as well as price volatility
before the change in the trading rule are higher than those after the
implementation of the trading rule. To better understand the difference, we plot the differences of volumes and volatilities under
the ‘‘T + 0’’ and ‘‘T + 1’’ trading rules for the 109 B-share stocks in
Fig. 1. The upper graph is the difference of volumes under the
‘‘T + 0’’ and ’’T + 1’’ trading rules. The middle graph is the difference
of volatilities measured by maximum and minimum price differences. The lower graph is the difference of volatilities measured
by the standard deviation of the return series. It is easy to see that
most stocks have lower average daily volumes under ‘‘T + 1’’ than
under ‘‘T + 0’’, and almost all stocks’ average volatilities are lower
under ‘‘T + 1’’ for both measures.
We conduct the Wilcoxon Signed Rank test of our hypotheses.10
The null hypothesis is that there is zero difference in trading volumes (and volatilities) due to the change of the trading rule, and
the alternative hypothesis is that the difference is greater than 0.
The results, summarized in Table 3, show that the differences in
trading volume and volatilities are significantly greater than 0.
However, another important policy change occurred in 2001 as
well. This policy allows domestic investors to invest in the B-share
market after February 19, 2001. This ‘‘Opening-up’’ policy attracted
more investors, hence more capital into the market. As the trading
volume and volatilities in the stock market are also affected by the
number of investors, it would be premature to conclude it is the
switch from ‘‘T + 0’’ to ‘‘T + 1’’ that caused the reduction of average
trading volume and volatilities. We check the robustness of our
test by taking into consideration the effect of the ‘‘Opening-up’’
policy, using two approaches.
First, it is worth noting that the ‘‘Opening-up’’ policy is introduced earlier than the ‘‘T + 1 trading rule’’. Therefore, if we use only
the sample data after the implementation of the ‘‘Opening-up’’ policy to conduct the Wilcoxon Signed Rank test for trading volume
and price volatilities, then our results are not driven by the ‘‘Opening-up’’ policy. There are two stages in the B-share market’s
‘‘Opening-up’’ policy. From February 19, 2001 to June 1, 2001,
domestic investors were only allowed to use deposits made to
domestic commercial banks before February 19. After June 1,
domestic investors were allowed to trade B-shares with deposits
made to domestic commercial banks after February 19, as well as
with foreign funds transferred from overseas. To account for the
potentially different impacts of these two stages, we construct
two samples in our empirical estimation: February 19, 2001 to
September 25, 2002, with 195 trading days before and after the
‘‘T + 1 trading rule’’, respectively, denoted as ‘‘Sample 1’’, and a
shorter sample period starting from June 1, 2001 to June 20,
2002 with 126 trading days before and after the ‘‘T + 1 trading
rule’’, respectively, denoted as ‘‘Sample 2’’.
We calculate the differences in trading volume and price volatilities as before. Because we use the data sampled after February
19, the date the ’’Opening-up’’ policy began, the differences of trading volume and price volatilities before and after ‘‘T + 1’’ exclude
the effect of the ’’Opening-up’’ policy, leaving only the effect of
the change in the trading rule. We conduct the Wilcoxon Signed
Rank test of our hypotheses. The null hypothesis is that there is
zero difference in trading volumes (and volatilities) due to the
change of trading rule, and the alternative hypothesis is that the
difference is greater than 0. The results, summarized in Table 4,
show both differences are still significantly greater than 0.
The second approach for checking the robustness is to separate
the effect of the ‘‘Opening-up’’ policy and the ‘‘T + 1 trading rule’’,
using two-year sample period data. Since the introduction of the
10
Wilcoxon Signed Rank test is a nonparametric test, commonly used to compare
two sample medians without the assumption of the distribution.
581
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
Denote V Tþ1=Tþ0 ¼ ln VV Tþ1
. We further decompose VT+1/T+0 into
Tþ0
the part which can be explained by the change in the trading rule
and explained by the increase in the number of shareholders,
Tþ1
NSTþ1=Tþ0 ¼ NS
, which is a proxy variable for the ‘‘Opening-up’’
NSTþ0
policy. This decomposition is in line with the spirit of our above
empirical analysis and separates the effects of the change of trading rule and the ’’Opening-up’’ policy. Following this logic, we conduct the following regression:
V Tþ1=Tþ0 ¼ a þ bNSTþ1=Tþ0 :
ð23Þ
V Tþ1
,
V Tþ0
Note that VT+1/T+0 is the logarithm of
thus if we can reject the
null hypothesis of ‘‘H0:a P 0’’, then we can conclude that volume
under the ’’T + 1 trading rule’’ is smaller. Thus the constant a measures the effect of the change from ‘‘T + 0’’ to ‘‘T + 1’’ and b measures
the effect of the ‘‘Opening-up’’ policy. Similarly, we define
!
highlow
Tþ1=Tþ0
r
!
rhighlow
rstd
Tþ1
and rstd
:
¼ ln Tþ1
Tþ1=Tþ0 ¼ ln
highlow
rstd
rTþ0
Tþ0
We have the following two regressions:
rhighlow
Tþ1=Tþ0 ¼ a þ bNSTþ1=Tþ0 ;
rstd
Tþ1=Tþ0 ¼ a þ bNSTþ1=Tþ0 :
Fig. 1. Differences of volumes and volatilities under ‘‘T + 0’’ and ‘‘T + 1’’ Trading
Rules, 1999–2003.
‘‘Opening-up’’ policy changes the number of investors participating
in the B-share market, we use the number of shareholders to capture the effects of the ’’Opening-up’’ policy. From the Wind Financial Database, we find the data regarding each B-share’s number of
shareholders for each year during our sample period from December 1999 to November 2003. Denote NST+0 as the average number
of shareholders under the ‘‘T + 0 trading rule’’ from December 1999
to November 2001 and NST+1as the average number of shareholders
under the ‘‘T + 1 trading rule’’ from December 2001 to November
Tþ1
2003. We define NSTþ1=Tþ0 ¼ NS
, which measures the increase of
NSTþ0
shareholders from ‘‘T + 0’’ to ‘‘T + 1’’. We summarize the descriptive
statistics for NST+0 and NST+1 in Table 5.
ð24Þ
ð25Þ
To further check the robustness, we also carry out our regression for different time horizons. We estimate our models using
samples within one-year and two-year observations, before and
after the switching of trading rules, respectively. We present the
results in Table 6.
Table 6 shows that the constant terms are significant at the 5%
significance level. A one-sided t-test can reject the null hypothesis
of ‘‘H0: a P 0’’ at the 5% significance level. Thus we can confirm
that volumes and volatilities are all smaller under the ‘‘T + 1 trading rule’’ than under the ‘‘T + 0 trading rule’’ after controlling for
the effect of the ‘‘Opening-up’’ policy.
It is worth noting that in Table 6, the coefficient of NST+1/T+0 is
negative but not significantly different from zero. This coefficient
measures the contribution of the ‘‘Opening-up’’ policy to volume
and volatility, which is driven by two offsetting effects. On the one
hand, the ‘‘Opening-up’’ policy brings more rational investors to
the B-share market. Competition among rational investors makes
intentional manipulation less effective. As a result, the trading volume and price volatility tend to decrease. The reduction in trading
volume and volatility is consistent with the argument that more
rational speculators stabilize asset prices, which dates back to
Friedman (1953).11 Tirole (1982) also shows that price bubbles rely
on the myopia of traders and that they disappear if traders are all rational. On the other hand, the ’’Opening-up’’ policy introduces more
irrational trend chasers to the B-share market as well, which leads to
stronger trend-chasing (a larger g). As shown in Sections 5.1 and 5.2,
both trading volume and price volatility are positively related to g.
Hence, volume and volatility tend to increase. Our empirical results
indicate that in China’s B-share market, these two effects roughly
offset each other, though the first effect is weakly stronger than the
second one. As the coefficient is not significantly different from zero,
this negative coefficient should not be overly emphasized.
7. Conclusion
China’s stock market adopts a unique ‘‘T + 1 trading rule’’: an
investor is only allowed to sell stocks he bought at least one day
prior, and is forbidden to sell stocks he bought during the same
day. In this paper, we develop a dynamic price manipulation model
to analyze the effects of the ‘‘T + 1 trading rule’’ in terms of trading
11
See also Shleifer and Vishny (1997).
582
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
Table 3
Results of Wilcoxon Signed Rank test.
Sample periods
Price volatility (rhigh–low)
Trading volume (V)
Test statistics
P-value
Price volatility (rstd)
1 year
2 years
1 year
2 years
1 year
2 years
8.84
2.2e16
8.42
2.2e16
9.06
2.2e16
7.85
2.2e15
8.83
2.2e16
8.83
2.2e16
Table 4
Results of test for the sample after ‘‘Opening-up’’ policy.
Sample periods
Price volatility (rhigh–low)
Trading volume (V)
Test statistics
P-value
Price volatility (rstd)
Sample 1
Sample 2
Sample 1
Sample 2
Sample 1
Sample 2
8.26
2.2e16
8.88
2.2e16
8.71
2.2e16
9.06
2.2e16
7.98
2.2e15
8.81
2.2e16
Table 5
Summary statistics for NST+0 and NST+1.
Sample periods
Standard deviation
Min
Max
Average number of shareholders under ‘‘T + 0’’
2 years
4.67e+4
1 year
5.09e+4
Mean
4.65e+4
4.95e+4
4.88e+3
5.13e+3
2.61e+5
2.69e+5
Average number of shareholders under ‘‘T + 1’’
2 years
5.67e+4
1 year
5.77e+4
4.78e+4
4.90e+4
1.06e+4
1.01e+4
2.65e+5
2.73e+5
Mathur (editor). Any remaining errors are our own. This project
is supported by the HFRI.
Table 6
Estimation results.a
Coefficients
2 years
1 year
0.6566⁄⁄
0.2810
0.0512
1.1131⁄⁄
0.2540
0.0260
0.4378⁄⁄
0.0404
0.0194
0.3149⁄⁄
0.0730
0.0206
0.4589⁄⁄
0.0275
0.0031
0.3672⁄
0.0594
0.0095
Regression (23)
a
b
R2
Regression (24)
a
b
R2
Regression (25)
a
b
R2
a
We have tested our models for heteroskedasticity by using White test at the
10% level of significance. In regression (23), we find the evidence of heteroskedasticity during the 2-year sample period. For volatilities, we find that there is no
heteroskedasticity in regression (24) and there is heteroskedasticity in regression
(25) during both sample periods. For the cases when there is heteroskedasticity, we
use the HC3 estimator (Huber, 1967 and White, 1980) for efficient estimation of
coefficients’ covariance matrix. For all of the models under both sample periods, we
can reject the null hypothesis of ‘‘H0: a P 0’’ at the 5% level of significance by a onesided t-test.
⁄
5% Level of significance.
⁄⁄
1% Level of significance.
volume, price volatility, and investors’ welfare. We compare it with
the usual ‘‘T + 0 trading rule’’ adopted by all other equity markets,
with respect to the above three aspects.
We show that the ‘‘T + 1 trading rule’’ can effectively reduce the
total trading volume and price volatility, and improves the trend
chasers’ welfare compared with the ‘‘T + 0 trading rule’’, when
the strength of trend-chasing is strong. An empirical test with data
from China’s B-share market strongly supports our theory.
Appendix A. Proof of Proposition 2
Step 1. We first consider the case where X 0 P X 0 . In this case, we
have a boundary solution, i.e., X ¼ maxfX 0 ; X 0 g ¼ X 0 .
Since X 0 X 0 ¼ 12 X 0 þ ðgkþ3ÞX
P 0, we thus have
4
XP
2
X0:
gk þ 3
Substituting X ¼ X 0 into (17) yields:
max 2X 2 þ ðgk þ 1ÞX 0 X X 20
X
0
ð26Þ
ðb Þ X P X 0 :
The first-order condition gives:
X0 ¼
gk þ 1
X0:
4
ð27Þ
Similar to the period
3 problem,
we have the period 1 solun
o
2
tion X ¼ max X 0 ; gkþ3
X0 .
We then solve the case where X 0 6 X 0 . In this case, we
obtain:
1
ðgk þ 3ÞX
:
X ¼ maxfX 0 ; X 0 g ¼ X 0 ¼ X 0 2
4
ð28Þ
Plugging Eq. (28) into (17) yields:
1
1
1
ðgk þ 7Þðgk 1ÞX 2 þ ðgk 1ÞX 0 X X 20
8
2
2
ðb Þ X P X 0 :
max
X
0
ð29Þ
Acknowledgements
We thank Qingying He, Minsoo Lee, Mike Pollinger and an
anonymous referee for helpful comments. We also thank Ike
The first-order condition gives:
X¼
2
X0;
gk þ 7
ð30Þ
583
M. Guo et al. / Journal of Banking & Finance 36 (2012) 575–583
Whether (30) is optimal depends on the sign of the secondorder derivative, i.e., the sign of SOC ¼ 18 ðgk þ 7Þðgk 1Þ.
Plugging Eq. (28) into X 0 6 X 0 yields:
1
ðgk þ 3ÞX
6 0:
X 0 X 0 ¼ X 0 þ
2
4
2
X0:
gk þ 3
ð31Þ
For the case where X 0 6 X 0 , we also need to consider two
subcases as well. The first subcase is gk < 1. Since SOC < 0,
the object function (29) is quadratic and concave. Because
2
2
X 0 6 gkþ7
X 0 6 gkþ3
X0 ,
the
optimal
solution
is
2
X ¼ gkþ7
X 0 . For the second subcase where gk P 1, the object function is quadratic and convex. Thus, it is maximized
2
2
at either X0 or ðgkþ3Þ
X 0 . Plugging X0 or ðgkþ3Þ
X 0 into Eq.
(29) shows that X⁄ = X0 is the optimal solution. Therefore,
we can summarize the above results obtained in Step 1 in
the following lemma.
n
o
2
0
Lemma 1. If X 0 P X 0 , then X ¼ max gkþ1
4 X 0 ; gkþ3 X 0 ; if X 0 < X
2
and gk < 1, then X ¼ gkþ7
X 0 ; if X 0 < X 0 and gk > 1, then X⁄ = X0.
Step 2. Lemma 1 gives only intermediate results for the strategic
trader’s optimal trading strategy. We next obtain the equilibrium results by comparing the expected utility of
wealth for the strategic trader in the cases of X 0 < X 0
and X 0 P X 0 . Simple calculation leads to the following
summary table.
Table A.1 presents the strategic trader’s optimal trading quantities in periods 1 and 3 and the corresponding expected utilities in
two cases. From this table, it is easy to derive the final equilibrium
trading strategy for the strategic trader. When gk > 1, the expected
utilities for the cases X 0 > X 0 and X 0 P X 0 are the same. Therefore, the optimal trading quantity of the strategic trader in period
0
1 is not unique. It is given by either X ¼ ðgkþ1ÞX
or X⁄ = X0. Cor4
respondingly, her optimal trading quantity in period 3 is given by
0
either X ¼ X 0 or X ¼ ðgkþ1ÞX
. When 0 < gk < 1, comparing the
4
expected utilities between the two cases yields:
ðgk þ 3ÞX 20 ðg 2 k2 þ 2gk 11ÞX 20
ð1 gkÞð5 þ gkÞ2
¼2
> 0:
2
gk þ 7
ðgk þ 3Þ
ðgk þ 7Þðgk þ 3Þ2
Therefore, the strategic trader’s optimal trading quantities in periods 1 and 3 are given by:
X ¼ X ¼ 2X 0
:
gk þ 7
X 0 P X 0
X
Rearrangement gives:
X6
Table A.1
The strategic trader’s optimal trading quantities and utilities.
⁄
X 0 < X 0
X
EU1
X⁄
X
EU1
ðg 2 k2 þ2gk7ÞX 20
8
ðg 2 k2 þ2gk11ÞX 20
ðgkþ3Þ2
X0
ðgkþ1ÞX 0
4
2X 0
gkþ7
2X 0
gkþ7
ðg 2 k2 þ2gk7ÞX 20
8
ðgkþ3ÞX 20
gkþ7
gk > 1
ðgkþ1ÞX 0
4
X0
0 < gk < 1
2X 0
gkþ3
X0
Note: EU1 is the expected utility in period 1.
References
Aggarwal, R.K., Wu, G., 2006. Stock market manipulation. Journal of Business 79,
1915–1953.
Allen, F., Gale, D., 1992. Stock-price manipulation. Review of Financial Studies 5,
503–529.
Brunnermeier, M., Pedersen, L., 2005. Predatory trading. Journal of Finance 60,
1825–1863.
DeLong, J.B., Shleifer, A., Summers, L.J., Waldmann, R.J., 1990. Positive feedback
investment strategies and destabilizing rational speculation. Journal of Finance
45, 379–395.
Friedman, M., 1953. The case for flexible exchange rates. In: Friedman, M. (Ed.),
Essays in Positive Economics. University of Chicago Press.
Garman, M., Klass, M., 1980. On the estimation of security price volatilities from
historical data. Journal of Business 63, 67–78.
Gelos, G.R., Wei, S., 2002. Transparency and international portfolio holdings.
Working Paper, IMF.
Hart, O., 1977. On the profitability of speculation. Quarterly Journal of Economics
101, 579–597.
Huber, P.J., 1967. The behavior of maximum likelihood estimates under nonstandard conditions. In: Proceeding of the Fifth Berkeley Symposium on
Mathematical Statistics and Probability, vol. 1, pp. 221–233.
Jarrow, R.A., 1992. Market manipulation, bubbles, corners, and short squeezes.
Journal of Financial and Quantitative Analysis 27, 311–336.
Kaniel, R., Saar, G., Titman, S., 2008. Individual investor trading and stock returns.
Journal of Finance 63, 272–310.
Kaniel, R., Liu, S., Saar, G., Titman, S., 2009. Individual investor trading and return
patterns around earnings announcements. Working Paper, CEPR.
Khwaja, A.I., Mian, A., 2005. Unchecked intermediaries: price manipulation in an
emerging stock market. Journal of Financial Economics 78, 203–241.
Mei, J., Wu, G., Zhou, C., 2004. Behavior based manipulation: theory and prosecution
evidence. Working Paper, New York University.
Merrick, J.J., Naik, N.Y., Yadav, P.K., 2005. Strategic trading behavior and price
distortion in a manipulated market: anatomy of a squeeze. Journal of Financial
Economics 77, 171–218.
Shleifer, A., Vishny, R., 1997. The limits of arbitrage. Journal of Finance 61, 35–55.
Subrahmanyam, A., 1991. Risk aversion, market liquidity, and price efficiency.
Review of Financial Studies 4, 417–441.
Tirole, J., 1982. On the possibility of speculation under rational expectations.
Econometrica 50, 1163–1181.
Vitale, P., 2000. Speculative noise trading and manipulation in the foreign exchange
market. Journal of International Money and Finance 19, 689–712.
White, H., 1980. A heteroskedastic-consistent covariance matrix estimator and a
direct test of heteroskedasticity. Econometrica 48, 817–838.