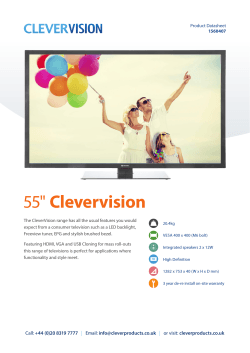
9HSTF MG*afi hii+
D e p a r t me nto fS i g na lP r o c e s s i nga ndA c o us t i c s J ussi Rämö Equal iz at io nT e c h nique s fo r H e adph o neL ist e ning Equal iz at io nT e c h nique sf o rH e adph o neL ist e ning J us s iR ämö A a l t oU ni v e r s i t y D O C T O R A L D I S S E R T A T I O N S Aalto University publication series DOCTORAL DISSERTATIONS 147/2014 Equalization Techniques for Headphone Listening Jussi Rämö A doctoral dissertation completed for the degree of Doctor of Science (Technology) to be defended, with the permission of the Aalto University School of Electrical Engineering, at a public examination held at the lecture hall S1 of the school on 31 October 2014 at 12. Aalto University School of Electrical Engineering Department of Signal Processing and Acoustics Supervising professor Prof. Vesa Välimäki Thesis advisor Prof. Vesa Välimäki Preliminary examiners Dr. Aki Härmä, Philips Research, The Netherlands Dr. Joshua D. Reiss, Queen Mary University of London, UK Opponent Dr. Sean Olive, Harman International, USA Aalto University publication series DOCTORAL DISSERTATIONS 147/2014 © Jussi Rämö ISBN 978-952-60-5878-8 ISBN 978-952-60-5879-5 (pdf) ISSN-L 1799-4934 ISSN 1799-4934 (printed) ISSN 1799-4942 (pdf) http://urn.fi/URN:ISBN:978-952-60-5879-5 Unigrafia Oy Helsinki 2014 Finland Abstract Aalto University, P.O. Box 11000, FI-00076 Aalto www.aalto.fi Author Jussi Rämö Name of the doctoral dissertation Equalization Techniques for Headphone Listening Publisher School of Electrical Engineering Unit Department of Signal Processing and Acoustics Series Aalto University publication series DOCTORAL DISSERTATIONS 147/2014 Field of research Acoustics and Audio Signal Processing Manuscript submitted 13 February 2014 Date of the defence 31 October 2014 Permission to publish granted (date) 6 August 2014 Language English Monograph Article dissertation (summary + original articles) Abstract The popularity of headphones has increased rapidly along with digital music and mobile phones. The environment in which headphones are used has also changed quite dramatically from silent to noisy, since people are increasingly using their headphones while commuting and traveling. Ambient noise affects the quality of the perceived music as well as compels people to listen to the music with higher volume levels. This dissertation explores headphone listening in the presence of ambient sounds. The ambient sounds can be either noise or informative sounds, such as speech. The first portion of this work addresses the first case, where the ambient sounds are undesirable noise that deteriorates the headphone listening experience. The second portion tackles the latter case, in which the ambient sounds are actually informative sounds that the user wants to hear while wearing headphones, such as in an augmented reality system. Regardless of the nature of the ambient sounds, the listening experience can be enhanced with the help of equalization. This work presents a virtual listening test environment for evaluating headphones in the presence of ambient noise. The simulation of headphones is implemented using digital filters, which enables arbitrary music and noise test signals in the listening test. The disturbing effect of ambient noise is examined with the help of a simulator utilizing an auditory masking model to simulate the timbre changes in music. Another study utilizes the same principles and introduces an adaptive equalizer for mitigation of the masking phenomenon. This psychoacoustic audio processing system was shown to retain reasonably low sound pressure levels while boosting the music, which is highly important from the viewpoint of hearing protection. Furthermore, two novel hear-through systems are proposed, the first of which is a digital augmented reality headset substituting and improving a previous analog system. The second system is intended to be worn during loud concerts as a user-controllable hearing protector and mixer. The main problem in both of the systems is the risk of a comb filtering effect, which can deteriorate the sound quality. However, it is shown that the comb filtering effect is not detrimental due to the passive isolation of an in-ear headset. Finally, an optimization algorithm for high-order graphic equalizer is developed, which optimizes the order of adjacent band filters to reduce ripple around the filter transition bands. Furthermore, a novel high-precision graphic equalizer is introduced based on parallel secondorder sections. The novel equalization techniques are intended for use not only in headphone applications, but also in wide range of other audio signal processing applications, which require highly selective equalizers. Keywords Acoustic signal processing, audio systems, augmented reality, digital filters, psychoacoustics ISBN (printed) 978-952-60-5878-8 ISBN (pdf) 978-952-60-5879-5 ISSN-L 1799-4934 ISSN (printed) 1799-4934 ISSN (pdf) 1799-4942 Location of publisher Helsinki Pages 151 Location of printing Helsinki Year 2014 urn http://urn.fi/URN:ISBN:978-952-60-5879-5 Tiivistelmä Aalto-yliopisto, PL 11000, 00076 Aalto www.aalto.fi Tekijä Jussi Rämö Väitöskirjan nimi Ekvalisointitekniikoita kuulokekuunteluun Julkaisija Sähkötekniikan korkeakoulu Yksikkö Signaalinkäsittelyn ja akustiikan laitos Sarja Aalto University publication series DOCTORAL DISSERTATIONS 147/2014 Tutkimusala Akustiikka ja äänenkäsittelytekniikka Käsikirjoituksen pvm 13.02.2014 Julkaisuluvan myöntämispäivä 06.08.2014 Monografia Väitöspäivä 31.10.2014 Kieli Englanti Yhdistelmäväitöskirja (yhteenveto-osa + erillisartikkelit) Tiivistelmä Digitaalisen musiikin ja matkapuhelimien yleistyminen ovat lisänneet kuulokkeiden suosiota. Samalla kuulokkeiden tavallinen käyttöympäristö on muuttunut hiljaisesta meluisaksi, sillä ihmiset käyttävät kuulokkeita liikkuessaan. Taustamelu vaikuttaa havaittuun äänenlaatuun ja myös pakottaa ihmiset kuuntelemaan musiikkia suuremmalla äänenvoimakkuudella. Tässä väitöskirjatyössä tutkitaan kuulokekuuntelua tilanteissa, joissa kuullaan myös ympäristöstä lähtöisin olevia ääniä. Ympäristön äänet voivat olla melua tai informatiivisia ääniä, kuten puhetta. Tämän työn ensimmäinen osa keskittyy tapaukseen, jossa ympäristön äänet ovat kuulokekuuntelua häiritsevää melua. Toisessa osassa ympäristön äänet ovat informatiivisia hyötyääniä, jotka käyttäjä haluaa kuulla vaikka käyttäisikin kuulokkeita, kuten esim. lisätyn todellisuuden järjestelmässä. Kummassakin tapauksessa kuulokekuuntelukokemusta voidaan parantaa ekvalisaattorin avulla. Tässä työssä esitetään virtuaalinen kuuntelukoeympäristö kuulokkeiden arviointiin melussa. Kuulokkeiden simulointi on toteutettu digitaalisilla suotimilla, jotka mahdollistavat mielivaltaisten testisignaalien käytön. Taustamelun aiheuttamaa peittoilmiötä tutkitaan simulaattorin avulla, joka hyödyntää auditiivista peittomallia simuloimaan havaittua musiikkia melussa. Samoja periaatteita hyödyntämällä on toteutettu myös psykoakustinen adaptiivinen ekvalisaattori, joka mukautuu kuunneltavaan musiikiin ja ympäristön meluun. Työssä näytettiin, että ekvalisaattori säilyttää musiikin kohtuullisen äänipainetason, koska se vahvistaa vain tarvittavia taajuusalueita. Tämä on erittäin tärkeää kuulovaurioiden ehkäisemisen kannalta. Työssä esitetään myös kaksi digitaalista läpikuuluvuussovellusta, joista ensimmäinen on analogisen järjestelmän paranneltu versio. Toinen sovellus on kehitetty konsertteja varten, joissa tarvitaan kuulonsuojausta. Sovellus mahdollistaa käyttäjäkohtaisen kuulonsuojauksen ja läpikuultavan musiikin ekvalisoinnin. Molempien sovellusten ongelmana on mahdollinen kampasuodinilmiö, joka voi heikentää järjestelmän äänenlaatua. Työssä kuitenkin osoitettiin, että kampasuodinilmiö on hallittavissa tulppakuulokkeiden hyvän vaimennuskyvyn ansiosta. Lisäksi tässä työssä kehitetään korkea-asteiselle graafiselle ekvalisaattorille optimointialgoritmi, joka vähentää ekvalisaattorin vasteen värähtelyä siirtymäkaistoilla. Tässä työssä kehitettiin myös uusi tarkka graafinen ekvalisaattori, joka perustuu rinnakkaisiin toisen asteen suotimiin. Uusia ekvalisointitekniikoita voidaan käyttää kuulokesovellusten lisäksi myös monissa muissa audiosignaalinkäsittelyn sovelluksissa. Avainsanat Akustinen signaalinkäsittely, audiojärjestelmät, digitaaliset suodattimet, lisätty todellisuus, psykoakustiikka ISBN (painettu) 978-952-60-5878-8 ISBN (pdf) 978-952-60-5879-5 ISSN-L 1799-4934 ISSN (painettu) 1799-4934 ISSN (pdf) 1799-4942 Julkaisupaikka Helsinki Sivumäärä 151 Painopaikka Helsinki Vuosi 2014 urn http://urn.fi/URN:ISBN:978-952-60-5879-5 Preface The work presented in this dissertation was carried out at the Department of Signal Processing and Acoustics at Aalto University School of Electrical Engineering in Espoo, Finland, during the period of September 2009 and October 2014. During this period, I have been lucky to have had the chance to be involved in various projects with Nokia Gear and Nokia Research Center. Without these great projects the writing of this thesis would not have been possible. I want to express my deepest gratitude to my supervisor Prof. Vesa Välimäki for all the guidance and support during the writing of this dissertation. Your guidance has been inspiring and invaluable. I am also extremely grateful to my first supervisor Prof. Matti Karjalainen who originally believed in me and gave me the chance to work in the acoustics lab back in 2008. I wish to thank my co-authors Dr. Miikka Tikander, Mr. Mikko Alanko, and Prof. Balázs Bank, for all your contributions. We managed to do pretty cool stuff together. I would also like to thank all the people from Nokia, with whom I have had the chance to work with during the projects. I also want to thank Luis Costa for proof-reading my work and constantly helping me to improve my writing skills. I would like to thank my pre-examiners Dr. Joshua D. Reiss and Dr. Aki Härmä, whose comments were valuable in further improving this dissertation. Thank you also to Dr. Sean Olive for agreeing to act as my opponent. As many have said before, the working environment in the acoustics lab is absolutely top-notch and I have had the pleasure to work with fantastic colleagues in the lab over the years. I would like to thank my co-workers: Sami, Julian, Heidi-Maria, Rafael, Stefano, Hannu, Jussi, Antti, Henkka, Pasi, Ole, Rémi, Jari, Jyri, Heikki T., Fabian, Atakan, 1 Preface Ville, Magge, Mikkis, Javier, Tapani, Olli, Marko, Ilkka, Tuomo, Teemu, Okko, Henna, Symeon, Archontis, Julia, Sofoklis, and all the other former and present people at the acoustics lab I have met during these years. Of course, I also need to thank all my friends outside the university who have helped me to maintain the balance between work and free-time. I am deeply grateful to my parents Arto Rämö and Heli Salmi for always believing and supporting me and showing pride in the things I do. I cannot thank you enough for that. Your support has been and still is extremely important to me. Finally, I would like to say special thanks to my girlfriend Minna for all the support and love you have shown me over the years. Espoo, September 18, 2014, Jussi Rämö 2 Contents Preface 1 Contents 3 List of Publications 5 Author’s Contribution 7 List of Symbols 9 List of Abbreviations 11 1. Introduction 13 2. Headset Acoustics and Measurements 17 2.1 Headphone Types . . . . . . . . . . . . . . . . . . . . . . . . . 17 2.2 Headset Acoustics . . . . . . . . . . . . . . . . . . . . . . . . . 18 2.3 Ear Canal Simulators . . . . . . . . . . . . . . . . . . . . . . . 20 2.4 Frequency Response Measurements . . . . . . . . . . . . . . 22 2.5 Headphone Equalization . . . . . . . . . . . . . . . . . . . . . 24 2.6 Ambient Noise Isolation . . . . . . . . . . . . . . . . . . . . . 25 2.7 Occlusion Effect . . . . . . . . . . . . . . . . . . . . . . . . . . 27 3. Augmented Reality Audio and Hear-Through Systems 29 3.1 Active Hearing Protection . . . . . . . . . . . . . . . . . . . . 29 3.2 Augmented Reality Audio . . . . . . . . . . . . . . . . . . . . 30 3.2.1 ARA Applications . . . . . . . . . . . . . . . . . . . . . 31 3.3 Comb-Filtering Effect . . . . . . . . . . . . . . . . . . . . . . . 32 4. Auditory Masking 35 4.1 Critical Bands . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 4.2 Estimation of Masking Threshold . . . . . . . . . . . . . . . . 36 3 Contents 4.3 Partial Masking . . . . . . . . . . . . . . . . . . . . . . . . . . 5. Digital Equalizers 38 39 5.1 Equalizers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39 5.2 Parametric Equalizer Design . . . . . . . . . . . . . . . . . . 41 5.3 High-Order Graphic Equalizer Design . . . . . . . . . . . . . 42 5.4 Parallel Equalizer Design . . . . . . . . . . . . . . . . . . . . 44 5.5 Comparison of the Graphic Equalizers . . . . . . . . . . . . . 46 6. Summary of Publications and Main Results 49 7. Conclusions 53 Bibliography 57 Errata 69 Publications 71 4 List of Publications This thesis consists of an overview and of the following publications which are referred to in the text by their Roman numerals. I J. Rämö and V. Välimäki. Signal Processing Framework for Virtual Headphone Listening Tests in a Noisy Environment. In Proc. AES 132th Convention, 6 pages, Budapest, Hungary, April 2012. II J. Rämö, V. Välimäki, M. Alanko, and M. Tikander. Perceptual Frequency Response Simulator for Music in Noisy Environments. In Proc. AES 45th Int. Conf., 10 pages, Helsinki, Finland, March 2012. III J. Rämö, V. Välimäki, and M. Tikander. Perceptual Headphone Equalization for Mitigation of Ambient Noise. In Proc. Int. Conf. Acoustics, Speech, and Signal Processing, pp. 724–728, Vancouver, Canada, May 2013. IV J. Rämö and V. Välimäki. Digital Augmented Reality Audio Headset. Journal of Electrical and Computer Engineering, Vol. 2012, Article ID 457374, 13 pages, September 2012. V J. Rämö, V. Välimäki, and M. Tikander. Live Sound Equalization and Attenuation with a Headset. In Proc. AES 51st Int. Conf., 8 pages, Helsinki, Finland, August 2013. VI J. Rämö and V. Välimäki. Optimizing a High-Order Graphic Equalizer for Audio Processing. IEEE Signal Processing Letters, Vol. 21, No. 3, pp. 301–305, March 2014. 5 List of Publications VII J. Rämö, V. Välimäki, and B. Bank. High-Precision Parallel Graphic Equalizer. IEEE/ACM Transactions on Audio, Speech and Language Processing, Vol. 22, No. 12, pp. 1894–1904, December 2014. 6 Author’s Contribution Publication I: “Signal Processing Framework for Virtual Headphone Listening Tests in a Noisy Environment” The author collaborated in the development of the filter design algorithms. He made the measurements and implemented the whole system by himself. He also wrote and presented the entire work. Publication II: “Perceptual Frequency Response Simulator for Music in Noisy Environments” The author conducted the measurements, listening tests, and implementation of the perceptual frequency response simulator in collaboration with the co-authors. Furthermore, the author wrote the article and presented it at the conference. Publication III: “Perceptual Headphone Equalization for Mitigation of Ambient Noise” The author collaborated in the algorithm development. He implemented the signal processing algorithms for the perceptual headphone equalizer. Furthermore, the author wrote and presented the entire paper. Publication IV: “Digital Augmented Reality Audio Headset” The author collaborated in the signal processing algorithm development. He implemented and wrote the work in its entirety except for the writing of abstract and conclusions. 7 Author’s Contribution Publication V: “Live Sound Equalization and Attenuation with a Headset” The author designed the system in collaboration with the co-authors, based on the original idea of the second author. The author programmed the Matlab simulator as well as the real-time demonstrator. Furthermore, the author wrote the article and presented it at the conference. Publication VI: “Optimizing a High-Order Graphic Equalizer for Audio Processing” The author discovered, designed, and implemented the optimization algorithm and was the main author of the paper. Publication VII: “High-Precision Parallel Graphic Equalizer” The author was responsible for coordinating and editing the work based on the idea of the co-authors. The author wrote the abstract and Sections I, IV, and V. He also collaborated in the algorithm design and implemented most of the new Matlab codes and examples as well as provided all the figures and tables included in the paper. 8 List of Symbols A(z) transfer function of an allpass filter a frequency parameter of the Regalia-Mitra filter ac frequency parameter of the Regalia-Mitra filter for cut cases ak,1 , ak,2 denominator coefficients of the parallel equalizer b allpass coefficient of the Regalia-Mitra filter bk,0 , bk,1 numerator coefficients of the parallel equalizer B two-slope spreading function c speed of sound f frequency in Hertz fr,open first quarter-wavelength resonance of an open ear canal fr,closed first quarter-wavelength resonance of a closed ear canal gd gain of direct sound geq gain of equalized sound h(t) impulse response of a system H(z) transfer function of a system K gain of the Regalia-Mitra filter L delay in samples LM sound pressure level of a masker l length of the ear canal leff effective length of the ear canal P number of filter sections r average radius of the ear canal U masking energy offset x(t) input signal (sine sweep) y(t) output signal (recorded sine sweep) ν frequency in Bark units Ω normalized filter bandwidth of the Regalia-Mitra filter ω0 normalized center frequency of the Regalia-Mitra filter 9 List of Symbols 10 List of Abbreviations ANC active noise control ARA augmented reality audio CPU central processing unit DRP drum reference point FIR finite impulse response FFT fast Fourier transform GPS Global Positioning System GPU graphics processing unit HRTF head-related transfer function IEC International Electrotechnical Commission IFFT inverse fast Fourier transform IIR infinite impulse response ISO International Organization for Standardization ITU-T International Telecommunication Union, Telecommunication Standardization Sector LPC linear prediction coefficients NIHL noise-induced hearing loss PGE parallel graphic equalizer SPL sound pressure level 11 List of Abbreviations 12 1. Introduction Nowadays many people listen to music through headphones mostly in noisy environments due to the widespread use of portable music players, mobile phones, and smartphones. Gartner Inc. reported that worldwide mobile phone sales to end users totaled 1.75 billion units in 2012, while the fourth quarter of 2012 realized a record in smartphone sales totaling over 207 million units, which was more than a 38 percent increase from the same quarter of 2011 [1]. However, already in the third quarter of 2013, smartphones sales reached over 250 million units, and the forecast of global mobile phone sales in 2013 is 1.81 billion units [2]. Almost all mobile phones, including low-priced budged phones, are capable of playing music and typically come with a stereo headset, which can also be used as a hands-free device (see Figure 1.1). Thus, basically everybody who owns a mobile phone is a potential headphone user. Due to the mobile nature of today’s headphone usage, the listening environments have also changed quite dramatically from quiet homes and offices to noisy streets and public transportation vehicles. The increased ambient noise of the mobile listening environments introduces a problem, since the noise masks the music by reducing its perceived loudness or by (a) (b) (c) Figure 1.1. Different mobile headsets, where (a) shows a smartphone and an in-ear headset, (b) shows a button-type headset, and (c) shows an on-the-ear headset. 13 Introduction masking parts of the music completely. This often leads to increased noise exposure levels, since people try to compensate the masking of the music by turning up the volume, which can increase the risk of hearing impairment. First, people should use suitable headphones that isolate ambient sounds well, and secondly, the ‘unmasking’ of the music signal should be done in a way that the level of the music is increased as little as possible. Additionally, now that people increasingly use their headphones, it is necessary to have a hear-through function in the headphones so that communication is easy and enjoyable even without removing the headphones. This requires built-in microphones and an equalizer to compensate for the changes that the headphones introduce to our outer ear acoustics. The ideal hear-through function, which is also the basis in augmented reality audio (ARA) [3], is to have completely transparent headphones that do not alter the timbre of the incoming sounds at all. This work considers how we can devise and assess improved signal processing approaches that enhance the experience of listening over headphones, including how to implement a psychoacoustically reasonable equalizer for headphones, especially for noisy environments, and how to further immerse headphone usage to be a part of our everyday lives. Thus, the main objectives of this dissertation are to 1. provide means to demonstrate the sound quality of different headphones especially in noisy environments, 2. enhance the mobile headphone listening experience using digital signal processing, 3. improve the precision of graphic equalizers, and 4. develop novel digital methods for hear-through systems. Objective 1 provides essential results that helps us to understand and experience how different types of headphones behave in a noisy environment. After understanding the principles of objective 1, it possible to devise novel signal processing methods, as defined in objective 2, which will enhance the headphone listening experience, e.g., by adaptively equalizing the music according to ambient noise. In order to equalize the music to mitigate the masking caused by ambient noise, it is necessary to satisfy 14 Introduction objective 3 and to design an equalizer with frequency selectivity similar to that of a human ear. Finally, to include headphones more into our everyday lives, the headphones should have a hear-through function that allows us to wear the headphones during conversations and to use them with augmented reality audio applications. The contents of this dissertation consist of this overview part accompanied by seven peer-reviewed publications, from which three have been published in international journals and four in international conferences. These publications tackle the research questions aiming to satisfy the objectives. Publications I, II, and III tackle the first objective by exploring headphone listening in noisy environments. Publication I introduces a test environment for virtual headphone listening tests, which also enables the evaluation of headphones in the presence of virtual ambient noise, whereas Publication II presents a perceptual frequency response simulator, which simulates the effect of the auditory masking caused by the ambient noise. Objective 2 is addressed especially in Publication III, which introduces an intelligent adaptive equalizer that is based on psychoacoustic models. However, the groundwork for Publication III is done in Publications I, II, and VI. Objective 3 is covered in Publications VI and VII, which present an optimizing algorithm for a high-order graphic equalizer and a novel high-precision graphic equalizer implemented with a parallel filter structure, respectively. The final objective is addressed in Publications IV and V, where digital hear-through systems are developed and evaluated. This overview part of this dissertation is organized as follows. Section 2 discusses headset acoustics and their measurement techniques, including ear canal simulators as well as magnitude frequency response and ambient noise isolation measurements. Section 3 introduces hear-through systems along with the concept and applications of augmented reality audio. Section 4 examines the auditory masking phenomenon, including the concepts of masking threshold and partial masking. Section 5 introduces digital equalizers, giving also three examples of digital equalizer filters used during this work. Section 6 summarizes the publications and their main results, and Section 7 concludes this overview part. 15 Introduction 16 2. Headset Acoustics and Measurements This section introduces basic headset acoustics and their measurement techniques. The focus is on in-ear headphones, since they are increasingly used in mobile music listening and in hands-free devices. Furthermore, in-ear headphones provide the tightest fit of all headphones, which leads to excellent ambient noise isolation, but at the same time introduces problems, such as unnatural ear canal resonances and the occlusion effect, due to the tightly blocked ear canal. The emphasis on the measurement techniques is on the frequency response and ambient noise isolation measurements, since they greatly affect the perceived sound quality in noisy environments. Section 2.1 provides a brief introduction to different headphone types and Section 2.2 introduces the basics of headphone acoustics, providing background information for Publications I through V. Section 2.3 describes the history and current status of ear canal simulators that are used in headphone measurements, related to Publications I–V. Sections 2.4 and 2.6 recapitulate frequency response and ambient noise isolation measurement procedures. Section 2.7 discusses the occlusion effect, which can easily degrade the user experience of an in-ear headset (Publications IV and V). 2.1 Headphone Types There are many different types of headphones, which all have their pros and cons in divergent listening environments. Furthermore, different applications set distinct requirements for headphones, such as size, ambient noise isolation, sound quality, and even cosmetic properties. ITU Telecommunication Standardization Sector (ITU-T) categorizes headphones into four groups: circum-aural, supra-aural, intra-concha, and in-ear/insert 17 Headset Acoustics and Measurements (a) (b) (c) (d) Figure 2.1. Categorization of headphones according to ITU-T Recommendation P.57, where (a) shows a circum-aural, (b) a supra-aural, (c) an intra-concha, and (d) an in-ear/insert headphone. Adapted from [4]. headphones [4]. Figure 2.1 shows the ITU-T categorization of the headphones, where (a) shows the circum-aural headphones, which are placed completely around the ear against the head; (b) shows the supra-aural headphones, which are placed on top of the pinna (also called on-the-ear headphones); (c) shows the intra-concha headphones (button-type), which are put loosely in the concha cavity; and (d) shows the in-ear headphones, which are inserted tightly into the ear canal (similarly to earplugs). When one or more microphones are wired to the headphones, they become a headset. Commonly, a mono microphone is installed in the wire of stereo headphones. Often, the casing of the in-wire microphone is also used as a remote control for the music player. When two microphones are mounted into headphones in a way that they are placed near the ear canal entrances of the user, the binaural cues of the user can be preserved well [5]. 2.2 Headset Acoustics Normally, when a person is listening to surrounding sounds with open ears, the incident sound waves are modified by the environment as well as by the listener’s torso, head, and outer ear. However, when the same surrounding sounds are captured with a conventional microphone and later reproduced using headphones, all these natural modifications are lost. Thus, headphone listening is quite different from the natural openear hearing that we are used to. Headphones also produce almost perfect channel separation between the left and right channels, which results in a situation where sound is perceived to come from inside the head. 18 Headset Acoustics and Measurements Headphones can alter the acoustics of the open ear canal by blocking it. This happens especially when using in-ear headphones, which tightly block the entrance of the ear canal. An open ear canal is basically a tube, which is open at one end and closed at the other by the ear drum. Thus, the open ear canal acts as a quarter-wavelength resonator, which has it first resonance at the frequency fr,open = c , 4leff (2.1) where c is the speed of sound and leff is the effective length of the ear canal. The effective length of the ear canal is slightly longer than the physical length due to the attached-mass effect [6]. The effective length of the ear canal (as an open-ended tube) can be estimated as leff = l + 8r/3π, (2.2) where r is the average radius and l is the physical length of the ear canal [6, 7]. An average ear canal has a length of approximately 27 mm and a diameter of about 7 mm [8]. When these measures are used in (2.1) and (2.2), the effective length leff is 30 mm and the first quarter-wavelength resonance occurs at the frequency of 2890 Hz, when the speed of sound is 346 m/s (corresponding to 25◦ C). Typically, the first resonance of the human ear is located around 3 kHz with the maximum boost of approximately 20 dB [9]. Figure 2.2 shows the effect of an open ear canal, where the contributions of the pinna, head, and upper torso are also included. The curve represents the difference between the magnitude response of a Genelec 8030A active monitor measured first 2 meters away in free-field, and then measured again from inside a human ear canal located 2 meters away. The microphone was placed 1 cm deep into the ear canal for the second measurement. As can be seen in Figure 2.2, the first quarter-wavelength resonance of this individual appears at 3.0 kHz. When the ear canal is blocked by an in-ear headphone, the ear canal acts as a half-wavelength resonator. The first half-wavelength resonance occurs at fr,closed = c . 2l (2.3) The insertion of the in-ear headphone also shortens the length of the ear canal (by approximately 5 mm) and increases the temperature of the air in the ear to be about 35◦ C [10]. The speed of sound at 35◦ C is approximately 19 Magnitude (dB) Headset Acoustics and Measurements 20 10 0 −10 100 1k Frequency (Hz) 10k Figure 2.2. Effect of the torso, outer ear, and ear canal on the magnitude of the frequency response measured approximately 1 cm deep from the ear canal of a human subject. The quarter-wavelength resonance, created by the open ear canal, appears at 3.0 kHz. 352 m/s. Using these measures in Equation (2.3), the first half-wavelength resonance of a closed ear canal occurs at 7180 Hz. Thus, the insertion of the headphone creates a new unnatural resonance as well as cancels the natural resonance people are used to hearing. 2.3 Ear Canal Simulators Headphones are typically measured using an ear canal simulator or a dummy head. The idea of both of the measurement devices is to mimic the actual average anatomy of the human ear canal, i.e., the measurement result should contain the ear canal resonances and the attenuation at low frequencies due to the eardrum impedance [11, 10]. The measurement device should also provide a natural fitting of the headphone to the measurement device. The sound pressure level (SPL), and thus also the magnitude response, created by a headphone in a cavity depends directly on the impedance of the cavity. The impedance of the cavity depends on the volume of the cavity and on the characteristics of anything connected to it [11]. In the case of an in-ear headphone inserted into an ear canal, there is a volume between the headphone tip and the eardrum (about 0.5 cm3 [11], and it depends on the in-ear headphone and the insertion depth of the headphone) as well as an acoustic compliance due to the middle ear cavity and the eardrum, which corresponds to a second volume (approximately 0.8 cm3 [11]). For low frequencies, the combined volume of 1.3 cm3 determines the impedance, and thus the SPL as well. When the 20 Headset Acoustics and Measurements frequency increases, the impedance changes from stiffness-controlled to mass-controlled as the mass of the eardrum becomes more significant (around 1.3 kHz) [10]. After that, the impedance corresponds only to that of the volume between the headphone tip and the eardrum (in this example 0.5 cm3 ), since the mass of the eardrum blocks the impedance of the middle ear [11, 10]. At higher frequencies, above around 7 kHz, the ear canal resonances affect the impedance the most [10]. One of the earliest endeavours to build a dummy head, which included a detailed structure of the pinnae as well as a correct representation of the ear canal up to the eardrum location, was conducted by Alvar Wilska in 1938 [12]. Wilska was actually a physician, and he had access to a morgue, where he was able to make a mold of the head of a male corpse. He then made a gypsum replica of the head with the ear regions formed from gelatine. He also built his own microphones (with a membrane diameter of 13 mm) and even installed the microphones at the eardrum location at an angle, which corresponds to the human anatomy [12]. The first headphone measurement devices were couplers that had a cylindrical volume and a calibrated microphone [11, 10], which simulated the acoustical load of an average adult ear. The couplers were mainly used to measure hearing aids and audiometry headphones. However, the simple cylindrical volume did not produce satisfactory results, which led to the development of more ear-like couplers [11, 13]. The pioneer of the modern ear simulator is Joseph Zwislocki, who designed an occluded ear canal simulator, which has a cylindrical cavity corresponding to the volume of the ear canal, a microphone positioned at the ear drum location called the drum reference point (DRP) [4], and a mechanical acoustic network simulating the acoustic impedance of the ear drum [14]. The acoustic network consists of several small cavities (typically from two to five), which are all connected to the main cylindrical cavity via a thin tube [11, 10]. The purpose of these thin tubes and cavities is to simulate the effective total volume of the ear, which changes with frequency, as explained above. As the frequency rises, the impedance of the thin tubes that connect the small cavities to the main cavity increases, which causes them to close off, and thus the effective volume of the simulator gradually falls from 1.3 cm3 to 0.6 cm3 , similarly as in the real ear [11]. Sachs and Burkhard [15, 16], Brüel [10], Voss and Allen [17], and Saltykov and Gebert [18] have evaluated the performance of the Zwislocki ear 21 Headset Acoustics and Measurements canal simulator and the previous 2 cm3 headphone couplers (often called 2cc couplers). Their results showed that even though there is a significant variability in the magnitude of the impedance for different human ear canals, the Zwislocki ear simulators produce reasonably accurate results when compared to real ear measurements, whereas the 2 cm3 calibration couplers give worse results. Futhermore, Sachs and Burkhard [15] suggested that better results could be achieved for the 2cc couplers, if an electronic correction filtering is applied. Today, the IEC 60318-4 Ed 1.0b:2010 [19] and ANSI S3.25–2009 [20] standards define the occluded ear simulators that are used to measure headphones. The occluded ear simulator can be used to measure in-ear headphones and hearing aids as such, and it can be extended to simulate the complete ear canal and the outer ear [19, 21, 22]. IEC 60318-4 (2010) defines the frequency range of the occluded ear canal simulator to be from 100 Hz to 10 kHz, whereas the previous standard IEC 60711, published in 1981, defined an upper frequency limit of 8 kHz. Furthermore, below 100 Hz and above 10 kHz, the simulator can be used as an acoustic coupler at frequencies down to 20 Hz and up to 16 kHz. However, the occluded ear simulator does not simulate the human ear accurately in the extended frequency range. 2.4 Frequency Response Measurements The frequency response measurement is a good way to study the performance of headphones. The magnitude frequency response shows the headphones’ ability to reproduce different audible frequencies, which determines the perceived timbral quality of the headphones. A widely used technique to measure frequency responses is a swept-sine technique. It has been proposed by Berkhout et al. [23], Griesinger [24, 25], Farina [26, 27], as well as Müller and Massarani [28]. The swept-sine technique as well as other measurement techniques are compared by Stan et al. [29]. The basic idea in sweep measurements is to apply a known signal x(t), which has a sinusoidal shape with exponentially increasing frequency, through the headphones, which are fitted in an ear canal simulator or a dummy head, and record the response of the system y(t) at the DRP. The impulse response of the system h(t) is calculated from the x(t) and 22 Headset Acoustics and Measurements −20 Magnitude (dB) −30 −40 −50 Circum−aural Supra−aural Intra−concha In−ear −60 −70 −80 100 1k Frequency (Hz) 10k Figure 2.3. Magnitude frequency responses of different headphones. y(t) with the fast Fourier transform (FFT) deconvolution h(t) = IFFT FFT(y(t)) , FFT(x(t)) (2.4) where IFFT is the inverse fast Fourier transform. Figure 2.3 shows four magnitude frequency responses of different headphones measured using a dummy head and the sine-sweep technique. The responses are normalized to have the same magnitude value at 1 kHz. As can be seen in the figure, the in-ear headphone has the strongest low frequency response. This is caused by the pressure chamber principle [30, 31], which affects low and middle frequencies, when sound is produced in small, airtight enclosures. The force of the headphone driver pumps the air inside the ear canal cavity producing a sound pressure proportional to the driver excursion. Moreover, when the wavelength is large compared to the dimensions of the ear canal (up to about 2 kHz [30]), the sound pressure is distributed uniformly in the volume, which enables the production of high SPLs at low frequencies. Thus, the pressure inside the closed ear canal is in phase with the volume displacement of the transducer membrane and the amplitude is proportional to that volume displacement [30]. The sine-sweep measurement technique was an essential tool in Publication I, but it was also utilized in Publications II–V and VII. Publication I introduced a signal processing framework for virtual headphone listening tests in simulated noisy environments. Briolle and Voinier proposed the idea of simulating headphones by using digital filters in 1992 [32]. Hirvonen et al. [33] presented a virtual headphone listening test methodology, which was implemented using dummy-head recordings. Hiekkanen 23 Headset Acoustics and Measurements et al. [34] have proposed a method to virtually evaluate and compare loudspeakers using calibrated headphones. Furthermore, a recent publication by Olive et al. [35] tackles the virtual headphone listening task by using infinite impulse response (IIR) filters constructed based on headphone measurements to simulate the headphones. Similarly as in [35], the main idea in Publication I is to simulate different headphones with digital filters, which allows the use of arbitrary music, speech, or noise as the source material. Thus, a wide range of impulse responses of different headphones were measured using the sine-sweep technique and a standardized head-and-torso simulator. The measured impulse responses were used as finite impulse response (FIR) filters to simulate the measured headphones. Furthermore, the ambient noise isolation capabilities of the headphones were also measured and simulated using FIR filters (see Section 2.6). 2.5 Headphone Equalization In the simulator of Publication I, all the modeled headphones are listened to through one pair of calibrated headphones. The pair of headphones used with the simulator must be compensated so that they introduce as little timbre coloration to the system as possible. This is done by flattening or whitening the headphone response. A typical method to implement the compensation of the headphones is to use an inverse IIR filter constructed from the magnitude response measurement of the headphone [33, 35]. Olive et al. [35] used a slightly smoothed minimum-phase IIR correction filter, which did not apply filtering above 10 kHz. Lorho [36] fitted a smooth curve to the headphone’s magnitude response to approximate the mean response of his measurements. The fitted curve had a flat low-frequency shape, the most accurate match in the range of 2–4 kHz (around where the first quarterwavelength resonance occurs), and a looser fit at high frequencies. Finally, he designed a linear-phase inverse filter from the smoothed approximation curve. There can be problems with the inverse filter when the measured magnitude response has deep notches, because they will convert into high peaks in the inversion. This was the case in [34] and in Publication I of this work. Hiekkanen et al. [34] first smoothed the measured magnitude response (with a moving 1/48-octave Hann window) and then inverted 24 Headset Acoustics and Measurements the smoothed response. They then calculated a reference level based on the average level of the inverted response (between 40–4000 Hz). After that, they compressed all the peaks (above 4 kHz) exceeding the reference level. Finally, they created a minimum-phase impulse response from the inverted and peak deducted magnitude response. In Publication I the measured magnitude response of the headphones was first modeled with linear prediction coefficients (LPC). The LPC technique results in a minimum-phase all-pole filter, which can easily be inverted without any stability issues. A peak reduction (or actually a notch reduction) technique was also used, and it was implemented by ’filling’ the notch in the measured magnitude response in the frequency domain, after which the LPC technique was applied to the corrected magnitude response where the notch was compensated. 2.6 Ambient Noise Isolation The isolation capabilities of headphones are determined by the physical structure of the headphones as well as by the coupling of the headphones to the user’s ears. Circum-aural and supra-aural headphones are typically coupled tightly against the head and the pinna, respectively. Furthermore, these headphones can have open or closed backs, where the open back refers to earphone shells with leakage routes intentionally built into them. Intra-concha headphones usually sit loosely in the concha cavity, thus providing poor ambient noise isolation for the user. However, in-ear headphones are used similarly as earplugs, and they are designed to have good isolation properties. Figure 2.4 shows the measured isolation curves of four different types of headphones. In Figure 2.4, zero dB means that there is no attenuation at all and negative values indicate increasing attenuation. The black curve illustrates the isolation of open-back circum-aural headphones, the green curve represents the isolation of closed-back supra-aural headphones, the red curve shows the isolation of intra-concha headphones, and finally the purple curve shows the isolation of in-ear headphones. As can be seen, the in-ear headphones have clearly the best ambient noise isolation capability of these headphones, while the open-back circum-aural and the intra-concha headphones have the worst sound isolation, as can be expected. The isolation properties of headphones are further explored in Publica- 25 Headset Acoustics and Measurements 10 Attenuation (dB) 0 −10 −20 −30 −40 −50 Circum−aural Supra−aural Intra−concha In−ear 100 1k Frequency (Hz) 10k Figure 2.4. Measured isolation curves of different headphone types. tions I–V, where the first three publications estimate and simulate the amount of ambient noise in the ear canal in a typical music listening and communication applications and the latter two consider how the leakage of ambient noise affects the hear-through applications (see Section 3). The isolation capabilities of headphones can be improved with active noise control (ANC) [37, 38, 39, 40, 41]. The idea in ANC is to actively reduce the ambient noise at the ear canal by creating an anti-noise signal, which has the same sound pressure in magnitude but is opposite in phase to the noise signal. The utilization of the ANC in headsets dates back to the 1950s, where Simshauser and Hawley [42] conducted pure-tone experiments with an ANC headset. The two basic forms of ANC are feedforward [40] and feedback systems [41]. The main difference in these systems is the position of the microphones that are used to capture ambient noise. Adaptive feedforward ANC uses an external reference microphone outside the headphone to capture the noise and a microphone inside the headphone to monitor the error signal. Feedback ANC has only the internal error microphone that is used to capture the noise and to monitor the error signal. The feedforward and feedback structures can also be combined to create more efficient noise attenuation [39, 43]. Figure 2.5 shows the effect of a feedback ANC, measured from a commercial closed-back circum-aural ANC headset. The feedback ANC works best at low frequencies, while it has a negligible effect at high frequencies. Furthermore, the feedback ANC typically amplifies the noise at its transition band, around 1 kHz [39], as shown in Figure 2.5. The transition band is the frequency band between the low frequencies, where the ANC 26 Headset Acoustics and Measurements 10 ANC off ANC on Attenuation (dB) 0 −10 −20 −30 −40 −50 100 1k Frequency (Hz) 10k Figure 2.5. Effect of active noise control. operates efficiently and the high frequencies, where the effect of the ANC is negligible. 2.7 Occlusion Effect The occlusion effect refers to a situation where one’s ears are blocked by a headset or a hearing aid and their own voice sounds loud and hollow. This effect is due to the bone conducted sounds that are conveyed to the ear canals [44]. The occlusion effect is experienced as annoying and unnatural, since the natural perception of one’s own voice is essential to normal communication [45]. With music listening this is rarely a problem, since the user rarely talks while listening to music. However, with ARA applications and hearing aids, the occlusion effect can be a real nuisance. Normally, when the ear canal is not blocked, the bone-conducted sounds can escape through the ear canal opening into the environment outside the ear and no extra sound pressure is generated in the ear canal [30, 46], as illustrated in Figure 2.6(a). This is the normal situation that people are used to hear. However, when the entrance of the ear canal is blocked, the perceived sound of one’s own voice is changed [45]. This is because the bone-conducted sounds that are now shut in the ear canal obey the pressure chamber principle, as discussed in Section 2.4. This amplifies the perception of the bone-conducted sounds when compared to the open ear case [30, 11, 47, 48, 46], as illustrated in Figure 2.6(b). In addition to the bone-conducted sounds, the air-conducted sounds are attenuated when the the ear canal is occluded, which further accentuates the distorted perception of one’s own voice [45]. 27 Headset Acoustics and Measurements Bone conducted sound Bone conducted sound p p (a) (b) Figure 2.6. Occlusion effect. Diagram (a) illustrates the open ear, where the bone conducted sound radiates through the ear canal opening and (b) illustrates the occluded ear, where the bone conducted sound is amplified inside the ear canal. Adapted from [30]. The occlusion effect can be passively reduced by introducing vents in the headset casing. However, the vents decrease the ambient noise isolation of the headset, which is usually undesirable. Furthermore, the vents increase the risk of acoustic feedback when the headset microphone is placed near the earpiece. The occlusion effect can also be reduced actively, which typically uses the active feedback cancellation method similarly as a feedback ANC. That is, there is an internal microphone inside the ear canal connected to the signal chain with a feedback loop [49]. According to Meija et al. [49], active occlusion reduction can provide 15 dB of occlusion reduction around 300 Hz, which results in a more natural perception of one’s own voice and therefore increases the comfort of using a headset. Furthermore, active occlusion reduction does not deteriorate the ambient noise isolation capability of a headset, since no additional vents or leakage paths are needed. 28 3. Augmented Reality Audio and Hear-Through Systems This section presents the concept of ARA as well as touches on the subject of active hearing protection. According to the World Health Organization [50], more than 360 million people have disabling hearing loss. The number is so large that the current production is less than 10 % of the global need. It is extremely important to protect one’s hearing, and not only from loud environmental noises, but also from loud music listening, which can cause hearing loss as well. Furthermore, it is widely accepted that temporary hearing impairments can lead to accumulated cellular damage, which can cause permanent hearing loss [51]. This section provides background information for Publications III, IV and V. 3.1 Active Hearing Protection Noise-induced hearing loss (NIHL) occurs when we are exposed to very loud sounds (over 100 dB) or sounds that are loud (over 85 dB) for a long period of time. NIHL can be roughly divided into two categories, namely work-related and self-imposed NIHLs. The first one can be controlled with regulations, which, e.g., enforce employees to wear hearing protection in loud working environments. However, laws or regulations cannot prevent self-imposed NIHL, such as that caused by listening to loud music or live concerts. People’s listening habits when using headphones have been studied, e.g., in [52, 53], where the highest user-set music levels reached over 100 dB in the presence of background noise [52]. Studies conducted during live music concerts [54, 55] indicate that the A-weighted exposure levels can exceed 100 dB during a concert. Furthermore, Clark et al. [54] discovered that five of the six subjects had significant hearing threshold shifts 29 Augmented Reality Audio and Hear-Through Systems (< 50 dB) mainly around the 4-kHz region after a rock concert. The hearing of all subjects returned to normal 16 hours after the concert. A major problem with passive hearing protection is that it impairs speech intelligibility as well as blocks informative sounds, such as alarms or instructions. With active hearing protectors, it is possible to implement a hear-through function, which lets low-level ambient sounds, such as speech, through the hearing protector by capturing the sounds with an included microphone and by reproducing them with a loudspeaker that is implemented in the hearing protector. When the level of the ambient sounds increases, the gain of the reproduced ambient sounds is decreased, and eventually when the gain goes to zero, the harmfully loud sounds are passively attenuated by the hearing protector [56]. Publications III and V tackle the NIHL problem by offering signal processing applications which reduce the noise exposure caused by music. Publication III introduces an intelligent, perceptually motivated equalizer for mobile headphone listening that adapts to different noisy environments. The idea is to boost only those frequency regions that actually need amplification, and in this way minimize the volume increase caused by the boosting. Publication V presents a hear-through application that can be used during a loud concert to limit the noise exposure caused by the live music. The hear-through function is user controllable, which allows the user to do some mixing of their own during the concert. Furthermore, the idea to enhance the target signal in the presence of noise is also used in mobile communication applications [57, 58, 59] as well as in automotive audio [60, 61]. In mobile communication applications, the target signal is typically speech, and this technique is called near-end listening enhancement. 3.2 Augmented Reality Audio Augmented reality is defined as a real-time combination of real and virtual worlds [3]. In ARA, a person’s natural sound environment is extended with virtual sounds by mixing the two together so that they are heard simultaneously. The mobile usage of ARA requires a headset with binaural microphones [62, 63, 64]. A prerequisite of an ARA headset is that it should be able to relay the natural sound environment captured by the microphones to the ear canal unaltered, and with minimal latency. This copy of the natural 30 Augmented Reality Audio and Hear-Through Systems Virtual sounds Binaural signals to distant user Figure 3.1. Block diagram of the ARA system. sound environment that has propagated through the ARA system is called a pseudoacoustic environment [3]. However, the acoustics of the ARA headset differs from normal open ear acoustics, and hence, the ARA headset requires equalization in order to sound natural. The equalization is realized with an ARA mixer [63]. The sound quality of the pseudoacoustic environment must be good so that the users can continuously wear the ARA headset without fatigue. The usability issues of the ARA headset have been studied by Tikander [65]. Because of the low latency requirements, earlier ARA systems were implemented using analog components [63] in order to avoid the combfiltering effect (see Section 3.3) caused by the delayed pseudoacoustic sound. Publication IV introduces a novel digital version of the ARA system, as well as analyses how the delay caused by the digital signal processing affects the perceived signal. 3.2.1 ARA Applications Figure 3.1 shows the system diagram for ARA applications. Virtual sounds can be processed, e.g., with head-related transfer functions (HRTF) to place the virtual sounds into the three dimensional space around the user [66, 67]. The ARA mixer and equalizer is used for the equalization of the pseudoacoustic representation as well as for routing and mixing of all the signals involved in the system. Furthermore, the binaural microphone signals can be sent to distant users for communication purposes. The ARA technology enables the implementation of different innovative applications, including applications in communication and information services, such as teleconferencing and binaural telephony with good telepresence [68, 69], since the remote user can hear the same pseudoacoustic environment as the near-end user does. 31 Augmented Reality Audio and Hear-Through Systems There are also many possible application scenarios when the position and orientation of the user is known, including an eyes-free navigation system [70, 71], the virtual tourist guide [65], and location-based games [72]. The positioning of the user can be done using the Global Positioning System (GPS) whereas determining of the user’s orientation requires head tracking [73]. The ARA system can also be used to increase situational awareness [56]. Furthermore, it is possible to estimate different acoustic parameters from the surrounding environment, such as room reflections [74] and reverberation time [75]. The ARA system could also be used as an assistive listening device. In Publication V, the hear-through headset is used to attenuate ambient sounds while the pseudoacoustic representation is made adjustable for the user. Enhancing ambient sounds would also be possible with current technology. The digital ARA technology presented in Publication IV would enable an adjustable platform for a user-controllable ARA system that could be individually tuned to the user’s needs. 3.3 Comb-Filtering Effect In ARA, the pseudoacoustic representation undergoes some amount of delay due to the equalization filters. However, the largest delays are typically caused by the analog-to-digital and digital-to-analog converters operating before and after the actual equalization, respectively. The delay of a laptop and an external FireWire audio interface measured in Publication IV, including both the delays of the analog-to-digital and the digitalto-analog converter, was 8.6 and 21 ms, respectively. Furthermore, the delay introduced by the converters of the DSP evaluation board used in Publication IV was approximately 0.95 ms. In addition to the pseudoacoustic sound, the ambient sounds leak through and around the ARA headset. The leaked sound and the delayed pseudoacoustic sound are summed at the ear drum of the user, and because of the delay, it can easily result in a comb-filtering effect [76, 77]. The combfiltering effect occurring in a hear-through device can be simulated with an FIR comb filter: H(z) = gd + geq z −L , (3.1) where gd is the gain for the direct leaked sound, geq is the gain for the equalized pseudoacoustic sound, and L is the delay in samples. 32 Augmented Reality Audio and Hear-Through Systems Magnitude (dB) 10 0 −10 −20 −30 −40 100 1k Frequency (Hz) 10k (a) Magnitude (dB) 10 0 −10 −20 −30 −40 100 1k Frequency (Hz) 10k (b) Figure 3.2. Magnitude frequency response of the FIR comb filter defined in Equation (3.1), when the delay is 2 ms. In (a) the values of gd and geq = 0.5 and in (b) gd = 0.1 and geq = 0.9. The worst-case scenario occurs when both of the signals have the same amount of energy gd = geq . Figure 3.2(a) shows the comb-filtering effect when the gains are set to gd = geq = 0.5 and the delay is 2 ms. The value of 0.5 for the gains was chosen because when the sum of the gains is one the top of the peaks lie at 0 dB. Figure 3.2(b) shows the magnitude response of an FIR comb filter described by Equation (3.1), when the delay between the signals is 2 ms, as for the filter used to obtain Figure 3.2(a). However, now the direct sound is attenuated 20 dB, and thus the values of gd and geq are 0.1 and 0.9, respectively. As can be seen, the dips are at the same frequencies as in Figure 3.2(a), but their depth is reduced dramatically. In fact, with the 20-dB attenuation, the depth of the dips is only 2 dB. The audibility of the comb-filtering effect has been previously studied, e.g., in [78, 79, 76]. The amount of attenuation needed between the direct and delayed sound for the comb-filtering coloration to be inaudible 33 Augmented Reality Audio and Hear-Through Systems depends on the delay and the type of audio that is listened to. The result of Schuller and Härmä [79] showed that the level difference between the direct and delayed sound should be around 26–30 dB in order to be inaudible. The result was averaged over different audio test material. Brunner et al. [76] conducted a listening test in order to determine the audibility of the comb-filtering effect for speech, piano, and snare drum test signals. Their results indicated that when the delay is 0.5–3 ms, which corresponds to a typical latency of an ARA headset system, the average level difference needed in order for the comb-filtering effect to be inaudible was approximately 12 dB for the speech and piano, and 17 dB for the snare drum sample. The highest required attenuations (based on single subjects) for the piano, speech, and snare drum samples, were 22, 23, and 27 dB, respectively. This kind of isolation cannot be accomplished with all headphones, but with in-ear headphones it is possible, since they can provide more than 20-dB attenuation above 1 kHz, as shown in Figure 2.4. Furthermore, the idea in the ARA system is to wear the headset continuously and not to compare the pseudoacoustic representation of the sound directly with the real-world sounds by removing the headset. This allows the user of the headset to get accustomed to minor timbral distortions. 34 4. Auditory Masking Psychoacoustics is aiming to understand and characterize human auditory perception, especially the time-frequency processing of the inner-ear [80]. Auditory masking is a common psychoacoustic phenomenon that occurs all the time in our hearing system. Auditory masking refers to a situation where one sound (a masker) affects the perceived loudness of another sound (a maskee). The maskee can either be completely masked to be inaudible by the masker or just reduced in loudness. The latter instance is referred to as partial masking. Auditory masking has been tackled for quite a long time. Fletcher and Munson [81] have studied the relation between the loudness of complex sounds and masking already back in 1937. Despite the long history of research in the area, the auditory system, including auditory masking and hearing models, is still an active research topic [82, 83]. Knowledge of auditory masking has also been utilized in audio coding for 35 years, since Schroeder et al. [84] studied the optimization of speech codecs by utilizing the knowledge of human auditory masking. The idea in audio coding is to identify irrelevant information by analyzing the audio signal and then reducing this information from the signal according to psychoacoustical principles, including the analysis of absolute threshold of hearing, the masking threshold, and the spreading of the masking across the critical bands [85, 86, 87]. This Section provides the psychoacoustic context for Publications II and III. 4.1 Critical Bands The critical band is an important concept when describing the time-frequency resolution of the human auditory system. Basically, it describes 35 Auditory Masking 30 100 1k 300 Frequency (Hz) 10k 3k Figure 4.1. Bark band edges on a logarithmic scale. how the basilar membrane interprets different frequencies. The mechanical properties of the basilar membrane change as a function of its position. At the beginning, the membrane is quite narrow and stiff, while at the end it is wider and less stiff [88]. Every position on the basilar membrane reacts differently to different frequencies. In fact, the basilar membrane conducts a frequency-to-position transformation of sound [89, 90, 91]. The critical bandwidth is based on the frequency-specific positions of the basilar membrane. The hearing system analyzes wide-band sound in a way that the sounds within one critical band are analyzed as a whole. In terms of auditory masking, this means that the level of masking within a critical band is constant [92]. The Bark scale was proposed by Zwicker in 1961 [93] to represent the critical bands such that one Bark corresponds to one critical band. The critical bands behave linearly up to 500 Hz, and after that the behavior is mainly logarithmic. Figure 4.1 plots the band edges of the Bark scale, as introduced in [93]. Furthermore, the conversion from frequency in Hertz to the Bark scale can be approximately calculated from ν = 13 arctan 0.76f kHz + 3.5 arctan f 7.5kHz 2 , (4.1) where f is the frequency in Hertz and ν is the mapped frequency in Bark units [94]. 4.2 Estimation of Masking Threshold In order to estimate the inaudible critical bands of the maskee in the presence of a masker, a masking threshold is calculated. According to Zwicker and Fastl [94], the masking threshold refers to the SPL needed for a maskee to be just audible in the presence of a masker. The calculation of masking threshold used in this work (Publications II and III) is based on an audio signal coding technique presented by Johnston [85]. There are 36 Auditory Masking Masking energy offset (U) Sp re ad i ng fu nc tio SPL (dB) n (B ) SPL of masker (LM) Critical band (Bark) Figure 4.2. Masking threshold estimation. more recent and advanced auditory models available as well, e.g., [95, 96]. Nevertheless, the technique by Johnston was chosen, since the applications in Publications II and III required only an estimate of the masking threshold and not more complex auditory models or attributes. The Johnston method provides a straightforward method to calculate the masking threshold, and it is sufficiently low in complexity to be implemented in real-time. The masking threshold is calculated in steps [85], including the following: calculating the energy of the masker signal, mapping the frequency scale onto the Bark scale and calculating the average energy for each critical band, applying a spreading function to each Bark band, summing the individual spread masking curves into one overall spread masking threshold, estimating the tonality of the masker and calculating the offset for the overall spread masking threshold, and finally, accounting for the absolute threshold of hearing. All the equations needed to calculate the masking threshold are found in Publications II and III. Figure 4.2 illustrates the masking threshold estimation of one Bark band, where LM is the energy of the Bark band, B is the spreading function, and U is the masking-energy offset. The masking-energy offset is determined based on the tonality of the masker that can be estimated using the spectral flatness measure, which is defined as the ratio of the geometric mean to the arithmetic mean of the power spectrum [85]. A ratio close to one indicates that the spectrum is flat and the signal has decorrelated noisy content, whereas a ratio close to zero implies that the spectrum has narrowband tonal components [80]. The masking energy offset is required since it is known that a noise-like masker masks more effectively than a tonal masker [95]. 37 Auditory Masking SPL (dB) Masker A B Ma ski ng thre sho ld Critical band (Bark) Figure 4.3. Partial masking effect, where two tones (unfilled markers) are in the presence of a masker. 4.3 Partial Masking The maskee is not necessarily masked completely in the presence of the masker. When the maskee is just above the masking threshold, it is audible but perceived to be reduced in loudness. In such a case, the maskee is partially masked. Thus, the masker does not only shift the absolute threshold of hearing to the masked threshold, but it also produces a masked loudness curve [94]. The effect of partial masking is the strongest near the masking threshold. When the level of the maskee increases, the effect of the partial masking decreases at a slightly faster rate. As the level of the maskee increases to a sufficiently high level, the effect of partial masking ends, and the maskee is perceived at the same level in the presence of the masker as in quiet [97]. Figure 4.3 shows a situation where two tones with the same SPL are in the presence of a masker, one of which is at slightly higher frequency (B) than the masker and the other at much lower frequency (A). The thick stem with the filled marker shows the SPL of the masker, whereas the two stems with unfilled round markers (A and B) indicate the SPL of the two tones. The triangle marker is the perceived SPL of the high-frequency tone. As can be seen in Figure 4.3, the high-frequency tone (B) is above the masking threshold but still close to it. Thus, the tone is audible but its perceived SPL is reduced, as indicated by the triangle marker. However, the low-frequency tone (A) is nowhere near the masking threshold, and thus, it is not affected by the masker at all. The low-frequency tone is perceived at the same level as it would be perceived without the masker. 38 5. Digital Equalizers This section presents the basics of digital equalizers, which are widely used in this work, as well as a parametric and a graphic equalizer design, since they are used in Publications II-VII. Furthermore, the concept of a parallel equalizer is introduced, since Publication VII is based on this concept. 5.1 Equalizers Equalizers are often used to correct the performance of audio systems. In fact, equalization can be said to be one of the most common and important audio processing methods. The expression ‘equalize’ originates from its early application, which was to flatten out a frequency response. However, nowadays, the objective is not necessarily to flatten out the frequency response, but to alter it to meet desired requirements. A certain set of filters is needed in the implementation of an equalizer. These equalizer filters can be tuned to adjust the equalizer to suit the given application. Typical equalizer filters are shelving filters and peak or notch filters. Shelving filters are used to weight low or high frequencies. High-frequency and low-frequency shelving filters boost or attenuate frequencies above or below the selected cut-off frequency, respectively. Shelving filters are usually found on the treble and bass controls of home and car audio systems. Shelving filters are useful when adjusting the overall tonal properties. However, more precise filters are often required. A peak or notch filter can be targeted to a specific frequency band at any desired frequency. The first time that an equalizer was used to improve the quality of reproduced sound was in the 1930s, when motion pictures with recorded sound tracks emerged. Sound recording systems as well as reproduction systems 39 Digital Equalizers Figure 5.1. Front panel of a graphic equalizer. that were installed in theaters were poor and thus needed equalization [98, 99]. The first stand-alone, fully digital equalizer was introduced in 1987 by Yamaha, namely the DEQ7, which included features such as 30 preset equalizer programs and a parametric equalizer [99, 100]. The two most common types of equalizers are the parametric [101, 102, 103, 104, 105] and graphic [106, 107, 108, 109, 110] equalizers. With a parametric equalizer, the user can control the center frequency, bandwidth, and gain of the equalizer filters, whereas with graphic equalizer the only user-controllable parameter is the gain. The gains are controlled using sliders that plot the approximate magnitude response of the equalizer, as shown in Figure 5.1. Nowadays equalizers are widely used in audio signal processing, which include a variety of applications, such as enhancing a loudspeaker response [111, 112, 113] as well as the interaction between a loudspeaker and a room [114, 115, 116, 117, 118], equalization of headphones in order to provide a natural music listening experience [36, 119, 120, 121, 122] or a natural hear-through experience [123, 124, 125, 126], and enhancement of recorded music [127, 128]. Furthermore, an equalizer can be considered to be a filter bank, since it has an array of bandpass filters that are used to control different subbands of the input signal. However, more advanced filter banks, such as quadrature mirror filter banks, are often implemented with the analysissynthesis system using multirate signal processing [129]. In the analysis bank, the signal is split into different bands, and the sub-bands are decimated by an appropriate factor. Then, the sub-band signals can be processed independently, for example, by using different coding or compressing the sub-bands differently. After that, the signal is reconstructed by interpolating the sub-band signals [129]. Although multirate filter banks 40 Digital Equalizers offer a wider range of signal processing possibilities, the advantage of an equalizer is that it does not require the splitting and reconstruction of the audio signal. 5.2 Parametric Equalizer Design Regalia and Mitra [101] introduced a digital parametric equalizer filter, which is based on an allpass filter structure. The Regalia–Mitra filter enables gain adjustments at specified frequencies, while it leaves the rest of the spectrum unaffected. Furthermore, the equalizer parameters can be individually tuned. The transfer function of the filter can be expressed as K 1 H(z) = [1 + A(z)] + [1 − A(z)], 2 2 (5.1) where K specifies the gain of the filter and A(z) is an allpass filter [101]. When A(z) is a first-order allpass, the filter is a shelving filter. When A(z) is a second-order allpass, the filter is a peak or notch filter. The secondorder allpass filter commonly used in (5.1) has the transfer function A(z) = a + b(1 + a)z −1 + z −2 , 1 + b(1 + a)z −1 + az −2 where a= 1 − tan(Ω/2) , 1 + tan(Ω/2) b = − cos(ω0 ), (5.2) (5.3) (5.4) Ω denotes the normalized filter bandwidth, and ω0 the normalized center frequency. When K > 1, the filter is a peak filter and when K < 1, it is notch filter. The peaks and notches are not symmetric in the original Regalia–Mitra filter structure, i.e., the bandwidth of the notches is smaller than that of the peak filters [101]. Figure 5.2(a) shows the asymmetry between the peak and notch filters. However, Zölzer and Boltze [130] extended the second-order Regalia-Mitra structure in order to have symmetrical peaks and notches. The only change to the original structure concerns the frequency parameter a, which becomes ac = K − tan Ω/2 , K + tan Ω/2 when K < 1. (5.5) Figure 5.2(b) shows the magnitude response of the peak and notch filters, when ac is used. 41 Digital Equalizers 20 10 10 0 0 −10 −10 Gain (dB) 20 −20 100 1k Frequency (Hz) 10k −20 100 (a) 1k Frequency (Hz) 10k (b) Figure 5.2. Effect of ac , where (a) is the response of the original Regalia-Mitra design and (b) is that of the improved design, which uses the ac parameter for notch filters. A slightly different approach to achieve the symmetry between the peaks and notches is presented by Fontana and Karjalainen [131]. Their implementation enables switching between peak and notch filter structures such that both structures share a common allpass section. 5.3 High-Order Graphic Equalizer Design Holters and Zölzer [108] presented a high-order graphic equalizer design with minimum-phase behavior. The equalizer has almost independent gain control at each band due to the high filter order. The design is based on a high-order digital parametric equalizer [132], which was later extended by Holters and Zölzer [133]. The design utilizes recursive filters, where fourth-order filter sections are cascaded in order to achieve higher filter orders. Figure 5.3 shows the recursive structure of the graphic equalizer, where P is the number of fourth-order sections that are cascaded. The dashed lines show the lower and upper limits of the ninth Bark band, whose center frequency is 1 kHz and bandwidth is 160 Hz. As can be seen, the filter becomes more and more accurate as the number of fourth-order sections is increased. A more detailed description of the filter design is given, e.g., in Publication VI. Publications II and III use a Bark-band graphic equalizer implemented using this high-order filter design [108]. The graphic equalizer in Publication II is used to simulate the perception of music in a noisy environment, i.e., the graphic equalizer is used to suppress those Bark bands that are either completely or partially masked by ambient noise. The masking information is obtained from psychoacoustical models, as described in Sec- 42 Digital Equalizers H1(z) H2(z) HP(z) Figure 5.3. High-order graphic equalizer, where the gain is set to -20 dB. The dashed line shows the lower and upper limit of the ninth Bark band. tion 4. Based on the estimate of the masking threshold and the partial masking effect, the gains of the high-order graphic equalizer are adjusted to suppress the music, so that if the energy of the music in a certain Bark band is below the masking threshold it is attenuated 50 dB. When the music is just partially masked, it is attenuated according to the partial masking model. The lessons learned from Publication II was then exploited in Publication III, where the design goal was to implement an adaptive perceptual equalizer for headphones which estimates the energy of the music and ambient noise inside the user’s ear canal based on the measured characteristics of the headphones. Furthermore, Publication VI introduces a novel filter optimization algorithm for the high-order graphic equalizer. Especially in the Bark-band implementation of the graphic equalizer, the errors in the magnitude response around the transition bands of the filters increase at high and low frequencies (due to the bilinear transform at high frequencies [108] and logarithmically non-uniform bandwidths at low frequencies). The errors occur due to the non-optimal overlapping of the adjacent filter slopes. The proposed optimization algorithm in Publication VI minimizes these errors by iteratively optimizing the orders of adjacent filters. The optimization affects the shape of the filter slope in the transition band, which makes the search for the optimum filter order possible by comparing it to the slope of the adjacent filter. Figure 5.4 shows the idea behind the optimization scheme, where in (a) the black curve is a target band filter (center frequency 350 Hz, bandwidth 100 Hz, gain −20 dB, and the number of fourth-order sections P = 2) and the colored curves are filter candidates of different order for the adjacent band (center frequency 250 Hz and bandwidth 100 Hz) with different number of fourth-order sections P = 2–5. As can be seen in Figure 5.4(a), 43 Digital Equalizers 0 3 Error (dB) −5 Magnitude (dB) P=2 P=3 P=4 P=5 −10 P=2 P=2 P=3 P=4 P=5 −15 −20 200 300 Frequency (Hz) 400 (a) 2 1 0 240 260 280 300 320 Frequency (Hz) 340 360 (b) Figure 5.4. Example of the interaction occurring around a transition band between two adjacent band filters, where (a) shows the magnitude response of a target band filter (black curve, P = 2) and a set of magnitude responses of filter candidates on the adjacent lower band (colored curves, P = 2, 3, 4, 5), and (b) shows the absolute errors around the transition band for the total filter responses (target is a flat curve in −20 dB). the shape of the filter slope changes when the filter order is increased. Figure 5.4(b) shows the absolute errors around the transition band (300 Hz), when the filters of different order (colored curves) are summed with the target filter (black curve). The target curve lies at −20 dB. As can be seen, the smallest peak error (approx. 1.5 dB, purple curve) occurs when the lower band filter has three fourth-order sections P = 3. The algorithm then chooses the number of fourth-order sections that results in the smallest peak error and moves to the next band and starts optimizing the order of that band filter by comparing it to the already optimized filter. 5.4 Parallel Equalizer Design The fixed-pole design of parallel equalizer filters was first introduced by Bank [134]. Since then, it has been utilized in different applications, such as magnitude response smoothing [135, 136], equalization of a loudspeaker-room response [135, 136], and modeling of musical instruments [134, 137, 138]. The design is based on parallel second-order IIR filters whose poles are set to predetermined positions according to the desired frequency resolution, which is directly affected by the pole frequency differences, i.e., the distance between adjacent poles. This enables a straightforward design of a logarithmic frequency resolution by placing the poles logarithmically, which closely corresponds to that of human hearing, and hence, it is of- 44 Digital Equalizers In b1,0 -a1,1 -a1,2 Out b1,1 H1(z) d0 Figure 5.5. Structure of the parallel equalizer. ten used in audio applications [139, 140]. The accuracy of the equalizer gets better when the number of the poles is increased. Furthermore, the accuracy increment can be targeted to a specified frequency area by placing more poles in that area. The poles can be set manually, as is done in Publication VII, or automatically, as shown, e.g., in [135, 118]. Other ways to achieve logarithmic frequency resolution include using warped filters [141] and more generalized Kautz filters [142, 143], where the frequency resolution can be set arbitrarily through the choice of the filter poles. Furthermore, Alku and Bäckström [144] introduced a linear prediction method which gives more accuracy at low frequencies. The method is based on conventional linear predictors of successive orders with parallel structures, which consist of symmetric linear predictors and lowpass and highpass pre-filters. Figure 5.5 shows the block diagram of the parallel filter structure, which consists of P parallel second-order sections (H1 (z), H2 (z), . . . , HP (z)) and a parallel direct path with a gain d0 . Thus, the transfer function of the parallel filter is H(z) = d0 + P bk,0 + bk,1 z −1 , 1 + ak,1 z −1 + ak,2 z −2 k=1 (5.6) where ak,1 and ak,2 are the denominator coefficients of the k th second-order section, which are derived based on the predetermined pole positions, and bk,0 and bk,1 are the numerator coefficients of the k th section, which are optimized based on the target response. 45 Digital Equalizers In Publication VII of this work, the filter design is done in the frequency domain [140, 145], since the parallel filter structure is used to implement a graphic equalizer, where the gain sliders define the target magnitude response. The phase of the target magnitude response is then set to be minimum phase. Furthermore, it is often useful to give different weights to different frequencies depending on the desired gain, when the magnitude error is minimized on a decibel scale, as discussed in Publication VII. Once the denominator coefficients and the target response have been determined, the numerator parameters can be solved using least-squares error minimization, as shown in Section III-B of Publication VII. This design is similar to the linear-in-parameter design of Kautz equalizers [142, 143]. In fact, the parallel filter structure produces effectively the same results as the Kautz filter but requires 33 % fewer operations, and has a fully parallel structure [146]. The benefit of the fully parallel structure is the possibility to use a graphics processing unit (GPU) instead of a central processing unit (CPU) to do the filtering [147]. GPUs have a large number of parallel processors, which can also be used to perform audio signal processing [148, 149]. 5.5 Comparison of the Graphic Equalizers Figure 5.6 shows the magnitude responses of both of the proposed graphic equalizers, when they have been configured for Bark-bands (25 bands). Figure 5.6(a) shows the magnitude response of the optimized high-order graphic equalizer, and Figure 5.6(b) shows the magnitude response of the parallel graphic equalizer (PGE). These two Bark-band graphic equalizers have the same command slider settings (round markers), which were chosen to have flat regions as well as large gain differences, both of which are known to be difficult challenges for a graphic equalizer. The orders of the equalizers differ quite radically. Starting from the first Bark band of the optimized high-order design shown in Figure 5.6(a), the number of the fourth-order sections are six, four, and three; bands from 4 to 23 have two fourth-order sections; and the last two bands have three and five sections, respectively, yielding a total order of 244. The parallel graphic equalizer shown in Figure 5.6(b) has 50 second-order sections, resulting in a total order of 100. Furthermore, the PGE design avoids the problem that typically occurs in graphic equalizers, where the interaction between the adjacent band 46 Digital Equalizers Magnitude (dB) 15 10 5 0 −5 −10 −15 100 1k Frequency (Hz) 10k (a) Magnitude (dB) 15 10 5 0 −5 −10 −15 100 1k Frequency (Hz) 10k (b) Figure 5.6. Comparison of two Bark-band graphic equalizers (25 bands). The figures show the magnitude response of (a) the optimized high-order equalizer design and (b) the parallel graphic equalizer design with the same command slider positions. The round markers indicate the command positions. filters cause errors in the magnitude response, as shown in the case of the high-order graphic equalizer in Figure 5.4(b). This problem is avoided because the parallel second-order sections are jointly optimized, as discussed in Publication VII. Comparing the PGE to the high-order graphic equalizer, the main difference between these two equalizers is that the joint optimization in the PGE enables smaller filter orders than the highorder graphic equalizer requires. One downside of the PGE is that every time a command slider position is altered by the user, the optimization has to be recalculated, whereas in the optimized high-order equalizer, the optimization is done only once, offline, and when the user changes the command setting of a band, only the fourth-order sections of that band must be recalculated. However, saving preset equalizer command settings for the PGE is highly efficient, since the filter optimization can be precomputed and easily stored in memory. 47 Digital Equalizers Both of these graphic equalizer designs can be widely used in audio signal processing applications. The high-order graphic equalizer results in more brick-wall-like filters than the smoother PGE due to the high filter order, as can be seen in Figure 5.6, especially around 400–1000 Hz and 2– 3 kHz. This feature makes the high-order graphic equalizer suitable, e.g., for the perceptual equalization applications presented in Publications II and III. 48 6. Summary of Publications and Main Results This section summarizes the main results presented in the publications. Publication I: "Signal Processing Framework for Virtual Headphone Listening Tests in a Noisy Environment" Publication I describes a signal processing framework that enables virtual listening of different headphones both in quiet and in virtual noisy environments. Ambient noise isolation of headphones has become an essential design feature, because headphones are increasingly used in noisy environments when commuting. Thus, it is important to evaluate the performance of the headphones in an authentic listening environment, since the headphones together with the ambient noise define the actual listening experience. The proposed framework provides just this by emulating the characteristics of the headphones, both the frequency response of the driver and the ambient sound isolation of the headphone, based on actual measurements. Furthermore, the proposed framework makes otherwise impractical blind headphone comparisons possible. Section 3 presents the calibration method of the reference headphones used during the listening, since the frequency response of the reference headphones must be compensated. This is done by using linear prediction filter coefficients to invert the measured frequency response of the reference headphones with the help of a peak reduction technique, also described in Section 2.5 of this overview part. Section 4 shows how the proposed framework is implemented using Matlab with Playrec and how the measured impulse responses are used as FIR filters to simulate the characteristics of the headphones. 49 Summary of Publications and Main Results Publication II: "Perceptual Frequency Response Simulator for Music in Noisy Environments" Publication II further tackles mobile headphone listening and the difficulties caused by ambient noise. Publication II expands on the fact that the listening environment drastically affects the headphone listening experience, as discussed in Publication I. A real-time perceptual simulator for music listening in noisy environments is presented. The simulator uses an auditory masking model to simulate how the ambient noise alters the perceived timbre of music. The auditory masking model is described in Section 3, which includes a masking threshold calculation (Sec. 3.1) and a partial masking model (Sec. 3.2) derived from a listening test with complex test sounds resembling musical sounds. Section 4 describes the implementation of the simulator, whose output is a music signal from which all components masked by the ambient noise as well as the noise itself are suppressed. This is done with a high-order Bark-band graphic equalizer, which is controlled by the psychoacoustic masking estimations. Furthermore, Section 5 presents the simulator evaluation results obtained from a listening test. Publication III: "Perceptual Headphone Equalization for Mitigation of Ambient Noise" Publication III uses the ideas and techniques developed in Publication II to enhance the listening experience in mobile headphone listening by equalizing the music. This is achieved by using the same psychoacoustic models that were used in Publication II to analyze ambient noise and music while simultaneously considering the characteristics of the headphones. This enables the estimation of the ambient noise and music level inside the ear canal. The ideal goal is to estimate the level to which the music should be raised to in order to have the same perceived tonal balance in a noisy mobile environment as in a quiet one. The same high-order Bark-band graphic equalizer as used in Publication II was utilized. Section 3 together with Figures 1 and 2 describe the implementation of the proposed perceptual headphone equalization. One of the main advantages of the proposed equalizer is that it retains a reasonable SPL after equalization, since the music is boosted only at those frequencies where needed. Thus, the system preserves the hearing of the user, when com- 50 Summary of Publications and Main Results pared to the typical case where the user just raises the volume of the music. The Matlab/Playrec implementation is also presented in Section 3. Publication IV: "Digital Augmented Reality Audio Headset" Publication IV introduces a novel digital design of an ARA headset. The ARA system has been commonly believed to require the delay in the processing chain to be as small as possible, since otherwise the perceived sound can be colored by the comb-filtering effect. This is the reason why earlier ARA systems have been implemented with analog components. However, the in-ear headphones used in this work provide a high isolation of the outside ambient sounds, which is beneficial with regard to the comb-filtering effect. Section 2 describes the physics behind the ARA technology as well as introduces possible applications to be used on the ARA platform. Sectiond 3 and 4 discuss the delays introduced by digital filters and passive mechanisms. Section 5 introduces the ARA equalizer filter design, which is implemented using a DSP evaluation board, as discussed in Section 6. Additionally, Section 6 presents how the measurements of the properties of the DSP board are made as well as a detailed analysis of the comb-filtering effect. Moreover, a listening test was conducted to subjectively evaluate the disturbance of a comb-filtering effect with music and speech signals. The digital implementation brings several benefits when compared to the old analog realization, such as the ease of design and programmability of the equalizer filters. Publication V: "Live Sound Equalization and Attenuation with a Headset" It was possible to implement a novel idea, where the user can control their surrounding soundscape during a live concert, based on the successful implementation of the digital augmented reality headset presented in Publication IV. Publication V presents a system, called LiveEQ, which captures ambient sounds around the user, provides a user-controllable equalization, and plays back the equalized ambient sounds to the user with headphones. An important feature of the LiveEQ system is that it also attenuates the perceived live music, since it exploits the high attenuation capability of in-ear headphones to provide hearing protection. The system was implemented using Matlab with Playrec as well as with 51 Summary of Publications and Main Results a DSP evaluation board. The Matlab implementation serves as a simulator whereas the DSP board implementation can be used in real time. Section 4.1 further examines the comb-filtering effect occurring in a hearthrough system that uses attenuative headphones. Publication VI: "Optimizing a High-Order Graphic Equalizer for Audio Processing" Publication VI presents a new optimization algorithm for the high-order graphic equalizer used in Publications II and III. The main idea is to optimize the filter orders to improve the accuracy and efficiency of the equalizer. Every practical filter has a transition band, and in the case of a graphic equalizer, each transition band interacts with its neighboring filters creating errors in the magnitude response. The proposed iterative algorithm minimizes these errors by optimizing the filter orders, which affects the shape of the transition band. The optimum shape of the transition band depends on the shape of the adjacent filter. The order optimization is executed only once offline, and after that, during the operation, only the gains of the graphic equalizer are changed according to the user’s command settings. The order optimization was shown to reduce the peak errors around the transition bands while the equalizer still had a lower filter order than non-optimized equalizers with larger errors. Publication VII: "High-Precision Graphic Parallel Equalizer" Publication VII introduces an accurate graphic equalizer whose design differs from that of the high-order equalizer used in Publication VI. The novel graphic equalizer is based on the parallel filter structure introduced in Section 5.4 of this overview. A typical problem with graphic equalizers is that the interaction between the adjacent filters, which can result in substantial errors especially with large boost or cut command settings. The advantage of the parallel design is that the filters are jointly optimized, and thus, the typical errors due to interaction of the filters are avoided. This enables the implementation of a highly accurate graphic equalizer. It was discovered that when there are twice as many pole frequencies compared to the number of the equalizer bands, the maximum error of the magnitude response of the proposed ±12-dB parallel graphic equalizer is less than 1 dB across the audible frequencies. 52 7. Conclusions This work explores equalization techniques for mobile headphone usage, including equalization of typical headphones as well as equalization of a hear-through headset. The mobile use of headphones has introduced new problems in music listening by degrading the perceived sound quality of the music. This is due to the ambient noise that leaks through the headphones into the ear canal. The ambient noise masks parts of the music and thus changes its perceived timbre. This is the reason why a good isolation capability is nowadays an important feature in mobile headphones. The degrading effect of ambient noise can be mitigated by using an intelligent equalization that enhances the music in those frequency regions where the auditory masking is pronounced. The ample isolation capability can sometimes be too much, especially in social situations. An ARA headset is a device that aims to produce a perfect hear-through experience with the possibility to include virtual sounds. The ambient sounds are captured with binaural microphones and reproduced with the headphone drivers. This requires equalization to compensate the alterations that the headset introduces to the acoustics of the outer ear. This overview of the dissertation presented background information that supports the included publications. The discussed topics include headphone acoustics and their measurements, an introduction to hear-through systems, as well as augmented reality audio and its applications. We also discussed digital equalizers and the matter of auditory masking, including the concepts of masking threshold and partial masking. Publication I presents a signal processing framework for virtual headphone listening tests, which includes the simulation of headphones’ ambient noise isolation characteristics. Publication II provides a simulator tool that helps one understand the auditory masking phenomenon in mo- 53 Conclusions bile headphone listening. Publication III is a sequel to Publication II, where the discovered results were utilized in an implementation of a perceptual equalizer for mobile headphone listening. Publications IV and V concentrate on hear-through applications. Publication IV presents the digital ARA headset, whereas Publication V presents a user-controllable hear-through application for equalizing live music and limiting the sound exposure during live concerts. The parts related to Publications II–V that could be expanded in the future are the usability and validation tests. Both of the systems introduced in Publications II and III would probably be more accurate should they be fine-tuned based on listening tests conducted in laboratory conditions as well as in real-life everyday situations. However, both of the proposed systems operate well as they are, and the perceptual equalizer introduced in Publication III provides an enhanced listening experience in noisy environments, while at the same time sustains restrained SPL. Moreover, the main issue in hear-through applications presented in Publications IV and V is the comb-filtering effect. However, it should also be tested how disturbing the comb-filtering effect actually is, when the user wears the hear-through system over long, continuous periods of time in different environments. Publication VI presents an optimization algorithm for a high-order graphic equalizer that iteratively optimizes the order of adjacent band filters. Publication VII presents a novel high-precision graphic equalizer, which is implemented using parallel second-order filters. The optimized highorder graphic equalizer enables brickwall-like filter responses, as demonstrated in Figure 5.3, which gives good accuracy for each band filter as well as for the whole equalizer, since the overlapping of the adjacent band filters are minimized. However, the filter orders must be quite large in order to create the brickwall filters. The PGE in Publication VII, on the other hand, avoids the filter overlapping issue by jointly optimizing the second-order sections. The resulting total order of the PGE can be significantly lower than that of the high-order equalizer; however, the PGE cannot create as steep band filter responses as the high-order equalizer, but results in a smoother overall magnitude response. Furthermore, the parallel structure of the graphic equalizer enables implementations using a GPU, which can often outperform a CPU in such a parallelizable task. Future research could address the following aspects and tasks that were not possible to be included in this work due to the time and space con- 54 Conclusions straints. First, a mobile implementation of the proposed equalization techniques and headphone applications would be important in order to allow real-life testing of the systems. The problem is the limited computing power of smartphones as well as the shortage of input channels (typically only one channel). However, the computing power of smartphones is constantly increasing, and modern smartphones can even be equipped with a GPU, which can enable utilization of parallel algorithms. Even then, the low power consumption, and thus low complexity algorithms, is a key requirement for smartphone applications. Another future study could include the development of algorithms reducing the comb-filtering effect in hear-through devices, which should be possible, since the equalized sound can be independently processed from the leaked sound. Furthermore, different hardware configurations should also be tested, since low-delay digital signal processors are widely available and they could reduce the disturbance of the comb-filtering effect. Of course, the ideal goal would be to implement all the proposed methods and more into a single pair of headphones. For example, it could include a user-controllable frequency response (arbitrary or based on existing measured responses), which could then be enhanced with an intelligent adaptive equalizer that keeps the perceived frequency response constant no matter what kind of noisy environment the user is in. Furthermore, the hear-through function should be fully adjustable from transparent hear-through to amplification and all the way to the most effective ANC-driven isolation. The adjusting of the hear-through can be automated based on the ambient noise and the content the user is listening to. Furthermore, it is possible to utilize other data provided by the user’s smartphone, such as location, network connections (WIFI and Bluetooth), time of day, and incoming phone calls, to control the properties of the headphones. It would also be useful in the future to measure a vast set of headphones, build a database, as well as implement and publish a listening test framework on the Internet that would be available to all who are interested in headphones. Based on the informal feedback from the users of the headphone simulator presented in Publication I, this appears to be a highly desired application for consumers. In the future, headphones could and probably will be used in assistive listening applications, where the idea is to improve the hearing of people with normal hearing in different situations. I believe that assistive 55 Conclusions listening applications will also create a need for novel signal processing methods and increase the usage of headphones in the future. 56 Bibliography [1] Gartner, Inc., “Gartner says worldwide mobile phone sales declined 1.7 percent in 2012,” http://www.gartner.com/newsroom/id/2335616, Feb. 2013. [2] ——, “Gartner says smartphone sales accounted for 55 percent of overall mobile phone sales in third quarter of 2013,” http://www.gartner.com/newsroom/id/2623415, Nov. 2013. [3] A. Härmä, J. Jakka, M. Tikander, M. Karjalainen, T. Lokki, J. Hiipakka, and G. Lorho, “Augmented reality audio for mobile and wearable appliances,” J. Audio Eng. Soc., vol. 52, pp. 618–639, Jun. 2004. [4] ITU-T, “Recommendation P.57, Series P: Telephone transmission quality, objective measuring apparatus - artificial ears,” International Telecommunication Union, Telecommunication Standardization Sector, Rec. ITU-T P.57, 2008/1996. [5] D. Hammershøi, “Fundamental aspects of the binaural recording and synthesis techniques,” in Proc. AES 100th Convention, Copenhagen, Denmark, May 1996. [6] R. Teranishi and E. A. G. Shaw, “External-ear acoustic models with simple geometry,” J. Acoust. Soc. Am., vol. 44, no. 1, pp. 257–263, 1968. [7] D. Raichel, The Science and Applications of Acoustics. Springer-Verlag, 2000. New York: [8] L. L. Beranek, Acoustics. New York: Acoustical Society of America through the American Institute of Physics, Inc., 1996. [9] F. M. Wiener and D. A. Ross, “The pressure distribution in the auditory canal in a progressive sound field,” J. Acoust. Soc. Am., vol. 18, no. 2, pp. 401–408, Oct. 1946. [10] P. Brüel, “Impedance of real and artificial ears,” Brüel & Kjær, Application Note, 1976. [11] H. Dillion, Hearing Aids. Sydney, Australia: Boomerang Press, 2001. [12] A. Wilska, “Studies on directional hearing,” Ph.D. dissertation, English translation, Aalto University School of Science and Technology, Dept. of Signal Processing and Acoustics, 2010. Ph.D. dissertation originally published in German as Untersuchungen über das Richtungshören, University of Helsinki, 1938. 57 Bibliography [13] M. D. Burkhard, “Measuring the constants of ear simulators,” J. Audio Eng. Soc., vol. 25, no. 12, pp. 1008–1015, Dec. 1977. [14] J. J. Zwislocki, “An ear-like coupler for calibration of earphones,” J. Acoust. Soc. Am., vol. 50, no. 1A, pp. 110–110, 1971. [15] R. M. Sachs and M. D. Burkhard, “Earphone pressure response in ears and couplers,” in Proc. 83rd Meeting of the Acoustical Society of America, Jun. 1972. [16] ——, “Zwislocki coupler evaluation with insert earphones,” Industrial Research Products, Inc. for Knowles Electronics, Inc., Tech. Rep., Nov. 1972. [17] S. E. Voss and J. B. Allen, “Measurement of acoustic impedance and reflectance in the human ear canal,” J. Acoust. Soc. Am., vol. 95, no. 1, pp. 372–384, Jan. 1994. [18] O. Saltykov and A. Gebert, “Potential errors of real-ear-to-couplerdifference method applied for a prediction of hearing aid performance in an individual ear,” in Proc. AES 47th International Conference, Chicago, USA, Jun. 2012. [19] IEC, “Electroacoustics—Simulator of human head and ear—Part 4: Occluded-ear simulator for the measurement of earphones coupled to the ear by means of ear inserts,” International Electrotechnical Comission, IEC 60318-4 Ed. 1.0 b:2010, Jan. 2010. [20] ANSI, “American national standard for an occluded ear simulator,” ANSI S3.25-2009, 2009. [21] S. Jønsson, B. Liu, A. Schuhmacher, and L. Nielsen, “Simulation of the IEC 60711 occluded ear simulator,” in Proc. AES 116th Convention, Berlin, Germany, May 2004. [22] K. Inanaga, T. Hara, G. Rasmussen, and Y. Riko, “Research on a measuring method of headphones and earphones using HATS,” in Proc. AES 125th Convention, San Francisco, CA, Oct. 2008. [23] A. J. Berkhout, D. de Vries, and M. M. Boone, “A new method to acuire impulse responses in concert halls,” J. Acoust. Soc. Am., vol. 68, no. 1, pp. 179–183, Jul. 1980. [24] D. Griesinger, “Impulse response measurements using all-pass deconvolution,” in Proc. AES 11th International Conference, Portland, Oregon, May 1992, pp. 306–321. [25] ——, “Beyond MLS—Occupied hall measurements with FFT techniques,” in Proc. AES 101st Convention, Los Angeles, California, Nov. 1996. [26] A. Farina, “Simultaneous measurement of impulse response and distortion with a swept-sine technique,” in Proc. AES 108th Convention, Paris, France, Feb. 2000. [27] ——, “Advancements in impulse response measurements by sine sweeps,” in Proc. AES 122nd Convention, Vienna, Austria, May 2007. [28] S. Müller and P. Massarani, “Transfer-function measurement with sweeps,” J. Audio Eng. Soc., vol. 49, no. 6, pp. 443–471, Jun. 2001. 58 Bibliography [29] G.-B. Stan, J.-J. Embrechts, and D. Archambeau, “Comparison of different impulse response measurement techniques,” J. Audio Eng. Soc., vol. 50, no. 4, pp. 249–262, Apr. 2002. [30] C. A. Poldy, “Headphones,” in Loudspeaker and Headphone Handbook, 3rd ed., J. Borwick, Ed. Focal Press, New York, 1994, pp. 585–692. [31] S. P. Gido, R. B. Schulein, and S. D. Ambrose, “Sound reproduction within a closed ear canal: Acoustical and physiological effects,” in Proc. AES 130th Convention, London, UK, May 2011. [32] F. Briolle and T. Voinier, “Transfer function and subjective quality of headphones: Part 2, subjective quality evaluations,” in AES 11th International Conference, Portland, OR, May 1992, pp. 254–259. [33] T. Hirvonen, M. Vaalgamaa, J. Backman, and M. Karjalainen, “Listening test methodology for headphone evaluation,” in Proc. AES 114th Convention, Amsterdam, The Netherlands, Mar. 2003. [34] T. Hiekkanen, A. Mäkivirta, and M. Karjalainen, “Virtualized listening tests for loudspeakers,” J. Audio Eng. Soc., vol. 57, no. 4, pp. 237–251, Apr. 2009. [35] S. E. Olive, T. Welti, and E. McMullin, “A virtual headphone listening test methodology,” in Proc. AES 51st International Conference, Helsinki, Finland, Aug. 2013. [36] G. Lorho, “Subjective evaluation of headphone target frequency responses,” in Proc. AES 126th Convention, Munich, Germany, May 2009. [37] P. A. Nelson and S. J. Elliott, Active Control of Sound. demic Press Limited, 1995. London, UK: Aca- [38] S. M. Kuo and D. R. Morgan, “Active noise control: A tutorial review,” Proceedings of the IEEE, vol. 87, no. 6, pp. 943–973, Jun. 1999. [39] B. Rafaely, “Active noise reducing headset—An overview,” in Proc. International Congress and Exhibition on Noise Control Engineering, The Hague, The Netherlands, Aug. 2001. [40] S. Priese, C. Bruhnken, D. Voss, J. Peissig, and E. Reithmeier, “Adaptive feedforward control for active noise cancellation in-ear headphones,” in Proc. Meeting on Acoustics, Acoustical Society of America, vol. 18, Jan. 2013. [41] C. Bruhnken, S. Priese, H. Foudhaili, J. Peissig, and E. Reithmeier, “Design of feedback controller for active noise control with in-ear headphones,” in Proc. Meeting on Acoustics, Acoustical Society of America, Jan. 2013. [42] E. D. Simshauser and M. E. Hawley, “The noise-cancelling headset—An active ear defender,” J. Acoust. Soc. Am., vol. 27, no. 1, pp. 207–207, 1955. [43] T. Schumacher, H. Krüger, M. Jeub, P. Vary, and C. Beaugeant, “Active noise control in headsets: A new approach for broadband feedback ANC,” in Proc. International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, May 2011, pp. 417–420. 59 Bibliography [44] G. V. Békésy, “The structure of the middle ear and the hearing of one’s own voice by bone conduction,” J. Acoust. Soc. Am., vol. 21, no. 3, pp. 217–232, May 1948. [45] C. Pörschmann, “One’s own voice in auditory virtual environments,” Acta Acustica united with Acustica, vol. 87, pp. 378–388, 2001. [46] J. Curran, “A forgotten technique for resolving the occlusion effect,” Starkey Audiology Series reprinted from Innovations, vol. 2, no. 2, 2012. [47] F. Kuk, D. Keenan, and C.-C. Lau, “Vent configurations on subjective and objective occlusion effect,” J. Am. Acad. Audiol., vol. 16, no. 9, pp. 747–762, 2005. [48] J. Kiessling, “Open fittings: Something new or old hat?” in Hearing Care for Adults First International Conference, (Chapter 17, pp. 217-226), Staefa, Switzerland, 2006. [49] J. Meija, H. Dillon, and M. Fisher, “Active cancellation of occlusion: An electronic vent for hearing aids and hearing protectors,” J. Acoust. Soc. Am., vol. 124, no. 1, pp. 235–240, Jul. 2008. [50] WHO, “World health organization. millions have hearing loss that can be improved or prevented,” Feb. 2013. [Online]. Available: www.who.int/mediacentre/news/notes/2013/hearing_loss_20130227/en/ [51] N. Petrescu, “Loud music listening,” McGill Journal of Medicine, vol. 11, no. 2, pp. 169–176, 2008. [52] E. Airo, J. Pekkarinen, and P. Olkinuora, “Listening to music with earphones: An assessment of noise exposure,” Acta Acustica united with Acustica, vol. 82, no. 6, pp. 885–894, Nov./Dec. 1996. [53] S. Oksanen, M. Hiipakka, and V. Sivonen, “Estimating individual sound pressure levels at the eardrum on music playback over insert headphones,” in Proc. AES 47th International Conference, Chicago, IL, Jun. 2012. [54] W. W. Clark and B. A. Bohne, “Temporary threshold shifts from attendance at a rock concert,” J. Acoust. Soc. Am. Suppl. 1, vol. 79, pp. 48–49, 1986. [55] R. Ordoñes, D. Hammershøi, C. Borg, and J. Voetmann, “A pilot study of changes in otoacoustic emissions after exposure to live music,” in Proc. AES 47th International Conference, Chicago, IL, Jun. 2012. [56] M. C. Killion, T. Monroe, and V. Drambarean, “Better protection from blasts without sacrificing situational awareness,” International Journal of Audiology, vol. 50, no. S1, pp. 38–45, Mar. 2011. [57] B. Sauert and P. Vary, “Recursive closed-form optimization of spectral audio power allocation for near end listening enhancement,” in ITGFachtagung Sprachkommunikation, Bochum, Germany, Oct. 2010. [58] ——, “Near end listening enhancement concidering thermal limit of mobile phone loudspeakers,” in Proc. 22. Konferenz Elektronische Sprachsignalverarbeitung, Aachen, Germany, Sept. 2011. 60 Bibliography [59] C. H. Taal, J. Jensen, and A. Leijon, “On optimal linear filtering of speech for near-end listening enhancement,” IEEE Signal Processing Letters, vol. 20, no. 3, pp. 225–228, Mar. 2013. [60] T. E. Miller and J. Barish, “Optimizing sound for listening in the presence of road noise,” in Proc. AES 95th Convetion, New York, NY, Oct. 1993. [61] M. Cristoph, “Noise dependent equalization control,” in Proc. AES 48th International Conference, Munich, Germany, Sept. 2012. [62] M. Tikander, M. Karjalainen, and V. Riikonen, “An augmented reality audio headset,” in Proc. 11th Int. Conference on Digital Audio Effects (DAFx08), Espoo, Finland, Sept. 2008. [63] V. Riikonen, M. Tikander, and M. Karjalainen, “An augmented reality audio mixer and equalizer,” in Proc. AES 124th Convention, Amsterdam, The Netherlands, May 2008. [64] D. Brungart, A. Kordik, C. Eades, and B. Simpson, “The effect of microphone placement on localization accuracy with electronic pass-through earplugs,” in Proc. IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA), New Paltz, NY, Oct. 2003. [65] M. Tikander, “Usability issues in listening to natural sounds with an augmented reality audio headset,” J. Audio Eng. Soc., vol. 57, no. 6, pp. 430– 441, Jun. 2009. [66] H. Møller, M. F. Sørensen, D. Hammershøi, and C. Jensen, “Head-related transfer functions of human subjects,” J. Audio Eng. Soc., vol. 43, no. 5, pp. 300–321, May 1995. [67] J. G. Bolaños and V. Pulkki, “HRIR database with measured actual source direction data,” in Proc. AES 133rd Convention, San Francisco, USA, Oct. 2012. [68] A. Härmä, J. Jakka, M. Tikander, M. Karjalainen, T. Lokki, H. Nironen, and S. Vesa, “Techniques and applications of wearable augmented reality audio,” in Proc. AES 114th Convention, Amsterdam, The Netherlands, Mar. 2003. [69] T. Lokki, H. Nironen, S. Vesa, L. Savioja, A. Härmä, and M. Karjalainen, “Application scenarios of wearable and mobile augmented reality audio,” in Proc. AES 116th Convention, Berlin, Germany, May 2004. [70] C. Dicke, J. Sodnik, and M. Billinghurst, “Spatial auditory interfaces compared to visual interfaces for mobile use in a driving task,” in Proc. Ninth International Conference on Enterprise Information Systems (ICEIS), Funchal, Madeira, Portugal, Jun. 2007, pp. 282–285. [71] B. F. G. Katz, S. Kammoun, G. Parseihian, O. Gutierrez, A. Brilhault, M. Auvray, P. Truillet, M. Denis, S. Thorpe, and C. Jouffrais, “NAVIG: augmented reality guidance system for the visually impaired,” Virtual Reality, vol. 16, pp. 253–269, 2012. [72] M. Peltola, T. Lokki, and L. Savioja, “Augmented reality audio for locationbased games,” in Proc. AES 35th International Conference, London, UK, Feb. 2009. 61 Bibliography [73] M. Karjalainen, M. Tikander, and A. Härmä, “Head-tracking and subject positioning using binaural headset microphones and common modulation anchor sources,” in Proc. International Conference on Acoustics, Speech and Signal Processing (ICASSP), Montreal, Canada, May 2004. [74] S. Vesa and T. Lokki, “Detection of room reflections from a binaural room impulse response,” in Proc. 9th Int. Conference in Digital Audio Effect (DAFx-06), Montreal, Canada, Sept. 2006, pp. 215–220. [75] S. Vesa and A. Härmä, “Automatic estimation of reverberation time from binaural signals,” in Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Philadelphia, USA, Mar. 2005, pp. 281–284. [76] S. Brunner, H.-J. Maempel, and S. Weinzierl, “On the audibility of combfilter distortions,” in Proc. AES 122nd Convention, Vienna, Austria, May 2007. [77] A. Clifford and J. D. Reiss, “Using delay estimation to reduce comb filtering of arbitary musical sources,” J. Audio Eng. Soc., vol. 61, no. 11, pp. 917– 927, Nov. 2013. [78] W. Ahnert, “Comb-filter distortions and their perception in sound reinforcement systems,” in AES 84th Convention, Paris, France, Mar. 1988. [79] G. Schuller and A. Härmä, “Low delay audio compression using predictive coding,” in IEEE Int. Conf. Acoust. Speech Signal Process., Orlando, FL, May 2002, pp. 1853–1856. [80] A. Spanias, T. Painter, and V. Atti, Audio Signal Processing and Coding. Hoboken, New Jersey: John Wiley & Sons, Inc., 2007. [81] H. Fletcher and W. A. Munson, “Relation between loudness and masking,” J. Acoust. Soc. Am., vol. 9, no. 1, pp. 1–10, Jul. 1937. [82] R. F. Lyon, A. G. Katsiamis, and E. M. Drakakis, “History and future of auditory filter models,” in Proc. IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, Jun. 2010, pp. 3809–3812. [83] J. Blauert, Ed., The Technology of Binaural Listening. Springer-Verlag, 2013. New York: [84] M. R. Schroeder, B. S. Atal, and J. L. Hall, “Optimizing digital speech coders by exploiting masking properties of the human ear,” J. Acoust. Soc. Am., vol. 66, no. 6, pp. 1647–1652, Dec. 1979. [85] J. D. Johnston, “Transform coding of audio signals using perceptual noise criteria,” IEEE Journal of Selected Areas in Communications, vol. 6, no. 2, pp. 314–323, Feb. 1988. [86] K. Brandenburg and D. Seitzer, “OCF: Coding high quality audio with data rates of 64 kbit/sec,” in Proc. AES 85th Convention, Los Angeles, CA, Nov. 1988. [87] K. Brandenburg and M. Bosi, “Overview of MPEG audio: Current and future standards for low-bit-rate audio coding,” J. Audio Eng. Soc., vol. 45, no. 1/2, pp. 4–21, Feb. 1997. 62 Bibliography [88] J. O. Pickles, An Introduction to the Physiology of Hearing. Academic Press Inc., 1982. London, UK: [89] D. D. Greenwood, “Critical bandwidth and the frequency coordinates of the basilar membrane,” J. Acoust. Soc. Am., vol. 33, no. 10, pp. 1344–1356, Oct. 1961. [90] ——, “A cochlear frequency-position function for several species–29 years later,” J. Acoust. Soc. Am., vol. 87, no. 6, pp. 2592–2605, Jun. 1990. [91] G. V. Békésy, Experiments in Hearing, E. G. Wever, Ed. McGraw–Hill Book Company, Inc., 1960. New York: [92] M. Bosi and R. E. Goldberg, Introduction to Digital Audio Coding and Standards. Boston, MA: Kluwer Academic, 2003. [93] E. Zwicker, “Subdivision of the audible frequency range into critical bands (frequenzgruppen),” J. Acoust. Soc. Am., vol. 33, no. 2, p. 248, Feb. 1961. [94] E. Zwicker and H. Fastl, Psychoacoustics: Facts and Models. Springer-Verlag, 1990. New York: [95] S. van de Par, A. Kohlrausch, G. Charestan, and R. Heusdens, “A new psychoacoustical masking model for audio coding applications,” in Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), May 2002, pp. 1805–1808. [96] M. L. Jepsen, S. D. Ewert, and T. Dau, “A computational model of human auditory signal processing and perception,” J. Acoust. Soc. Am., vol. 124, no. 1, pp. 422–438, Jul. 2008. [97] H. Gockel and B. C. J. Moore, “Asymmetry of masking between complex tones and noise: Partial loudness,” J. Acoust. Soc. Am., vol. 114, no. 1, pp. 349–360, Jul. 2003. [98] W. C. Miller, “Basis of motion picture sound,” in Motion Picture Sound Engineering, 6th ed. D. Van Nostrand Company, Inc., New York, 1938, ch. 1, pp. 1–10. [99] D. A. Bohn, “Operator adjustable equalizers: An overview,” in Proc. AES 6th International Conference, May 1988, pp. 369–381. [100] Yamaha, Digital Equalizer DEQ7, Operating Manual. [Online]. Available: http://www2.yamaha.co.jp/manual/pdf/pa/english/signal/DEQ7E.pdf [101] P. Regalia and S. Mitra, “Tunable digital frequency response equalization filters,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 35, no. 1, pp. 118–120, Jan. 1987. [102] T. van Waterschoot and M. Moonen, “A pole-zero placement technique for designing second-order IIR parametric equalizer filters,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 15, no. 8, pp. 2561– 2565, Nov. 2007. [103] H. Behrends, A. von dem Knesebeck, W. Bradinal, P. Neumann, and U. Zölzer, “Automatic equalization using parametric IIR filters,” J. Audio Eng. Soc., vol. 59, pp. 102–109, Mar. 2011. 63 Bibliography [104] J. D. Reiss, “Design of audio parametric equalizer filters directly in the digital domain,” IEEE Transactions on Audio Speech and Language Processing, vol. 19, no. 6, pp. 1843–1848, Aug. 2011. [105] S. Särkkä and A. Huovilainen, “Accurate discretization of analog audio filters with application to parametric equalizer design,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 19, no. 8, pp. 2486–2493, Nov. 2011. [106] D. A. Bohn, “Constant-Q graphic equalizers,” J. Audio Eng. Soc., vol. 34, no. 9, pp. 611–626, Sept. 1986. [107] S. Azizi, “A new concept of interference compensation for parametric for parametric and graphic equalizer banks,” in Proc. AES 112th Convention, Munich, Germany, May 2002. [108] M. Holters and U. Zölzer, “Graphic equalizer design using higher-order recursive filters,” in Proc. Int. Conf. Digital Audio Effects (DAFx-06), Sept. 2006, pp. 37–40. [109] S. Tassart, “Graphical equalization using interpolated filter banks,” J. Audio Eng. Soc., vol. 61, no. 5, pp. 263–279, May 2013. [110] Z. Chen, G. S. Geng, F. L. Yin, and J. Hao, “A pre-distortion based design method for digital audio graphic equalizer,” Digital Signal Processing, vol. 25, pp. 269–302, Feb. 2014. [111] M. Karjalainen, E. Piirilä, A. Järvinen, and J. Huopaniemi, “Comparison of loudspeaker equalization methods based on DSP techniques,” J. Audio Eng. Soc., vol. 47, no. 1-2, pp. 15–31, Jan./Feb. 1999. [112] A. Marques and D. Freitas, “Infinite impulse response (IIR) inverse filter design for the equalization of non-minimum phase loudspeaker systems,” in Proc. IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, Oct. 2005, pp. 170–173. [113] G. Ramos and J. J. López, “Filter design method for loudspeaker equalization based on IIR parametric filters,” J. Audio Eng. Soc., vol. 54, no. 12, pp. 1162–1178, Dec. 2006. [114] J. N. Mourjopoulos, “Digital equalization of room acoustics,” J. Audio Eng. Soc., vol. 42, no. 11, pp. 884–900, Nov. 1994. [115] M. Karjalainen, P. A. A. Esquef, P. Antsalo, A. Mäkivirta, and V. Välimäki, “Frequency-zooming ARMA modeling of resonant and reverberant systems,” J. Audio Eng. Soc., vol. 50, no. 12, pp. 1012–1029, Dec. 2002. [116] A. Mäkivirta, P. Antsalo, M. Karjalainen, and V. Välimäki, “Modal equalization of loudspeaker-room responses at low frequencies,” J. Audio Eng. Soc., vol. 51, no. 5, pp. 324–343, May 2003. [117] A. Carini, S. Cecchi, F. Piazza, I. Omiciuolo, and G. L. Sicuranza, “Multiple position room response equalization in frequency domain,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 20, no. 1, pp. 122– 135, Jan. 2012. 64 Bibliography [118] B. Bank, “Loudspeaker and room equalization using parallel filters: Comparison of pole positioning strategies,” in Proc. AES 51st International Conference, Helsinki, Finland, Aug. 2013. [119] A. Lindau and F. Brinkmann, “Perceptual evaluation of headphone compensation in binaural synthesis based on non-individual recordings,” J. Audio Eng. Soc., vol. 60, no. 1/2, pp. 54–62, Jan./Feb. 2012. [120] S. E. Olive and T. Welti, “The relationship between perception and measurement of headphone sound quality,” in Proc. AES 133rd Convention, San Francisco, CA, Oct. 2012. [121] S. E. Olive, T. Welti, and E. McMullin, “Listener preference for different headphone target response curves,” in Proc. AES 134th Convention, Rome, Italy, May 2013. [122] ——, “Listener preferences for in-room loudspeaker and headphone target responses,” in Proc. AES 135th Convention, New York, NY, Oct. 2013. [123] M. Tikander, “Usability issues in listening to natural sounds with an augmented reality audio headset,” J. Audio Eng. Soc., vol. 57, no. 6, pp. 430– 441, Jun. 2009. [124] D. Hammershøi and P. F. Hoffmann, “Control of earphone produced binaural signals,” in Proc. Forum Acousticum, Aalborg, Denmark, Jun. 2011, pp. 2235–2239. [125] P. F. Hoffmann, F. Christensen, and D. Hammershøi, “Quantitative assessment of spatial sound distortion by the semi-ideal recording point of hearthrough device,” in Proc. Meetings on Acoustics, vol. 19, Montreal, Canada, Jun. 2013. [126] ——, “Insert earphone calibration for hear-through options,” in Proc. AES 51st International Conference, Helsinki, Finland, Aug. 2013. [127] E. Perez Gonzales and J. Reiss, “Automatic equalization of multi-channel audio using cross-adaptive methods,” in Proc. AES 127th Convention, New York, NY, Oct. 2009. [128] Z. Ma, J. D. Reiss, and D. A. A. Black, “Implementation of an intelligent equalization tool using Yule-Walker for music mixing and mastering,” in Proc. AES 134th Convention, Rome, Italy, May 2013. [129] P. P. Vaidyanathan, Multirate Systems and Filter Banks. Cliffs, New Jersey: Prentice-Hall, Inc., 1993. Englewood [130] U. Zölzer and T. Boltze, “Parametric digital filter structures,” in AES 99th Convention, New York, NY, Oct. 1995. [131] F. Fontana and M. Karjalainen, “A digital bandpass/bandstop complementary equalization filter with independent tuning characteristics,” IEEE Signal Processing Letters, vol. 10, no. 4, pp. 119–112, Apr. 2003. [132] S. J. Orfanidis, “High-order digital parametric equalizer design,” J. Audio Eng. Soc., vol. 53, no. 11, pp. 1026–1046, Nov. 2005. [133] M. Holters and U. Zölzer, “Parametric recursive high-order shelving filters,” in AES 120th Convention, Paris, France, May 2006. 65 Bibliography [134] B. Bank, “Direct design of parallel second-order filters for instrument body modeling,” in Proc. International Computer Music Conference, Copenhagen, Denmark, Aug. 2007, pp. 458–465, URL: http://www.acoustics.hut.fi/go/icmc07-parfilt. [135] B. Bank and G. Ramos, “Improved pole positioning for parallel filters based on spectral smoothing and multi-band warping,” IEEE Signal Processing Letters, vol. 18, no. 5, pp. 299–302, Mar. 2011. [136] B. Bank, “Audio equalization with fixed-pole parallel filters: An efficient alternative to complex smoothing,” J. Audio Eng. Soc., vol. 61, no. 1/2, pp. 39–49, Jan. 2013. [137] B. Bank and M. Karjalainen, “Passive admittance synthesis for sound synthesis applications,” in Proc. Acoustics’08 Paris International Conference, Paris, France, Jun. 2008. [138] ——, “Passive admittance matrix modeling for guitar synthesis,” in Proc 13th International Conference on Digital Audio Effects (DAFx-10), Graz, Austria, Sept. 2010, pp. 3–7. [139] A. Härmä and T. Paatero, “Discrete representation of signals on a logarithmic frequency scale,” in Proc. IEEE Workshop on the Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, Oct. 2001, pp. 39–42. [140] B. Bank, “Logarithmic frequency scale parallel filter design with complex and magnitude-only specifications,” IEEE Signal Processing Letters, vol. 18, no. 2, pp. 138–141, Feb. 2011. [141] A. Härmä, M. Karjalainen, L. Savioja, V. Välimäki, U. K. Laine, and J. Huopaniemi, “Frequency-warped signal processing for audio applications,” J. Audio Eng. Soc., vol. 48, no. 11, pp. 1011–1031, Nov. 2000. [142] T. Paatero and M. Karjalainen, “Kautz filters and generalized frequency resolution: Theory and audio applications,” J. Audio Eng. Soc., vol. 51, no. 1–2, pp. 27–44, Jan./Feb. 2003. [143] M. Karjalainen and T. Paatero, “Equalization of loudspeaker and room responses using Kautz filters: Direct least squares design,” EURASIP Journal on Advances in Signal Processing, vol. 2007, 13 pages, Jul. 2007. [144] P. Alku and T. Bäckström, “Linear predictive method for improved spectral modeling of lower frequencies of speech with small prediction errors,” IEEE Trans. Speech and Audio Processing, vol. 12, no. 2, pp. 93–99, Mar. 2004. [145] B. Bank, “Magnitude-priority filter design for audio applications,” in Proc. AES 132nd Convention, Budapest, Hungary, Apr. 2012. [146] ——, “Perceptually motivated audio equalization using fixed-pole parallel second-order filters,” IEEE Signal Processing Letters, vol. 15, pp. 477–480, May 2008, URL: http://www.acoustics.hut.fi/go/spl08-parfilt. [147] J. A. Belloch, B. Bank, L. Savioja, A. Gonzalez, and V. Välimäki, “Multichannel IIR filtering of audio signals using a GPU,” in IEEE International Conference on Acoustic, Speech and Signal Processing (ICASSP), Florence, Italy, May 2014, pp. 6692–6696. 66 Bibliography [148] L. Savioja, V. Välimäki, and J. O. Smith, “Audio signal processing using graphics processing units,” J. Audio Eng. Soc., vol. 59, no. 1/2, pp. 3–19, Jan./Feb. 2011. [149] J. A. Belloch, M. Ferrer, A. Gonzalez, F. J. Martinez-Zaldivar, and A. M. Vidal, “Headphone-based virtual spatialization of sound with a GPU accelerator,” J. Audio Eng. Soc., vol. 61, no. 7/8, pp. 546–561, Jul./Aug. 2013. 67 A al t o D D1 4 7 / 2 0 1 4 9HSTFMG*afihii+ I S BN9 7 89 5 2 6 0 5 87 88 I S BN9 7 89 5 2 6 0 5 87 9 5( p d f ) I S S N L1 7 9 9 4 9 34 I S S N1 7 9 9 4 9 34 I S S N1 7 9 9 4 9 4 2( p d f ) A a l t oU ni v e r s i t y S c h o o lo fE l e c t r i c a lE ng i ne e r i ng D e p a r t me nto fS i g na lP r o c e s s i nga ndA c o us t i c s w w w . a a l t o . f i BU S I N E S S+ E C O N O M Y A R T+ D E S I G N+ A R C H I T E C T U R E S C I E N C E+ T E C H N O L O G Y C R O S S O V E R D O C T O R A L D I S S E R T A T I O N S
© Copyright 2026