Download Report

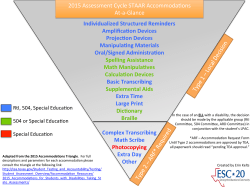
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
Blue – Rates
1.
A bricklayer can lay 8 bricks every 12 minutes. What is his rate of brick laying per
hour?
2.
A car travels 80 km in 90 minutes. What is its speed in km/h?
3.
A forestry worker can plant 126 pine seedlings in 40 minutes. How many pine
seedlings would he plant in 3 hours?
4.
If it takes 5 hours for a person to stack 1080 bales of hay, how long would it take
the same person to stack 756 bales?
5.
Bill spends $70 out of every $80 he earns. If he saves $250 each month, what is his
monthly income?
6.
For every $15 that a company earned during a charity fund raising, the company kept
$12 and the rest was given to charity. How much more did the company keep than
give to charity if it gave $1500 to clarity?
7.
Gina can wash 20 bowls for every 15 bowls that Margaret washes. If both of them
wash a total of 210 bowls, how many more bowls does Gina wash than Margaret?
8.
5 cm on a map represents an actual distance of 100 km.
a. What is the actual distance represented by 12 cm on the map?
b. What is the distance on the map representing an actual distance of 1260 km?
9.
The table shows the rate of charges in a parking lot.
First hour part thereof
$3.50
Every subsequent half an hour or part thereof
$2.50
Jaclyn parked her car in the parking lot from 10:20 a.m. to 1:30 p.m. How much did
she pay for the parking charges?
10. The table shows the rates of taxi fare.
First km
$2.40
Every subsequent 200 m or part thereof
$0.10
Sally traveled 26.9 km on a taxi. How much taxi fare did she pay?
11. It cost $2.50 to rent a badminton court per hour or part thereof between 9:00 a.m.
and 6:00 p.m., and $3.50 per hour or part thereof between 6:00 p.m. and 10:00 p.m.
Jennifer rented two badminton courts from 4:30 p.m. to 7:10 p.m. How much money
did she pay?
1
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
12. A taxi charged $2.20 for the first 2 mile travelled and $0.10 for each additional
half-mile or part thereof. Janet took a taxi from her house to the airport, which was
23.4 mi away. If she paid the driver $20, how much change did she get?
13. A book distributor charges $19.90 for the first book ordered through a book order.
It charges $17.50 for each of the next 4 books and $16.90 for every subsequent
book thereafter. How much must Peter pay if he were to order 10 books through this
book order?
14. It cost $12 to send a type A package and $18 to send a type B package. Albert sent
some type A and type B packages and paid $612 altogether. If he sent 9 type A
packages, how many type B packages did he send?
15. The table below shows the rates of charge for household water usage.
For the first 75 units
$0.20 per unit
For the next 100 units
$0.30 per unit
For the nest 125 units thereafter
$0.40 per unit
For all units thereafter
$0.50 per unit
If a certain household has to pay $110 for water usage this month, how many units of
water has it used?
16. A Pound of Tea
Jonathan and Hazel love to drink tea. When they are both at home, a pound of tea
lasts two weeks. Occasionally Hazel visits her mother in Australia. It takes six weeks
for Jonathan alone to use up a pound of tea.
How long should a pound of tea last Hazel if she were alone?
Remember to explain how you solved the problem.
Extra: In 2006 Hazel visited her mother for six weeks in the spring. In the summer
Jonathan gave up drinking tea for six weeks. Their favorite tea costs $9.00 per
pound. About how much did the couple spend on tea during the year? Explain.
17. The Big Balloon Blowup
Ulrike and Lars were helping with preparations for a fall party. One of their tasks
was blowing up balloons for some of the games that would be played.
Ulrike can blow up a balloon in 5 seconds. Lars can blow up a balloon in 6 seconds.
Ulrike takes 3 seconds to tie each balloon and Lars takes 4 seconds to tie each
balloon. Together they blew up and tied three bags of balloons in 14 minutes.
How many balloons were in each bag?
2
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
18. Horton's Clover Hunt
I have always loved the story Horton Hears a Who! by Dr. Seuss. For
those of you who aren't familiar with this particular tale, Horton the
elephant takes on the task of protecting tiny creatures living on a
dust speck that he has placed on a clover.
At one point in the story, a bird steals the clover from Horton and
drops it over a very large clover field at 6:56 a.m. Ever the faithful protector and
true to his promise to save them, "Because, after all, a person's a person, no matter
how small" Horton begins the enormous task of searching for the lost clover.
But clover, by clover, by clover he found
That the one that he sought for was just not around.
And by noon poor old Horton, more dead than alive,
Had picked, searched, and piled up, nine thousand and five.
For each of the answers below, round to the nearest whole unit.
1. At this rate, estimate how many clovers Horton picked each minute.
2. Approximately how many seconds did Horton spend on each clover?
Extra: The story continues
Then, on through the afternoon, hour after hour...
Till he found them at last! On the three millionth flower!
You need only choose one of these questions to answer:
A. If Horton continued at the rate you calculated above without pausing, how long
would it take him to reach the three millionth flower? Be sure to answer this
question in a way that makes sense (in other words, don't give an answer like 72
hours when 3 days would give us a better sense of how long this is).
or
B. In the story it seems that Horton finds the clover later the same day. If he
continued picking from noon until he found the clover at six o'clock that same
evening, approximately how fast would he have to work?
19. Water Fun?
Yesterday at 4:13 our 30-gallon water heater sprung a leak. It was spraying out
water at a rate of 2 tablespoons per second. Fortunately, we discovered the leak
right away and turned it off.
What I'd like to know is what time the water heater would have been empty if we
hadn't discovered the problem. We'll assume that the water heater was not refilling
itself at the same time it was leaking. Note: there are 16 tablespoons in 1 cup, 4 cups
in 1 quart, and 4 quarts in 1 gallon.
3
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
Bonus: What time would the water heater have been empty had the water been
spewing out at a rate of 3 tablespoons per second?
Solutions
1.
40 bricks/hours
2. 53.3 km/hr
3. 567 pine seedlings
4.
3.5 hours
5. $2000
6. $4500
7.
30
8. a. 240 km
b. 63 cm
9. $16
10. $15.40
11. $24
12. $13.50
13. $174.40
14. 28
15. 330
16. My final solution to "A Pound of Tea" is 3 weeks. My final solution to "Extra" is
$207.00 spent.
A Pound of Tea
If Jonathan drinks 1 lb in 6 weeks, that equals 1/6 lb per week, in 2 weeks Jonathan
will drink 2/6 lb (1/3 lb). If Jonathan drinks 2/6 lb in 2 weeks and Jonathan and
Hayzel together will drink 1 lb in 2 weeks, Hazel will drink 4/6 (6/6 - 2/6=4/6) lbs in
2 weeks. For each week Hazel drinks = 2/6 or 1/3 lb per week. For Hazel to drink 1 lb
it will take her 3 weeks.
Extra: There are 52 weeks in a year. Jonathan is away for 6 weeks in the summer
and Hazel is away for 6 weeks in the spring. It means that Jonathan drank tea for 46
weeks and Hazel also drank for 46 weeks (52-6). Jonathan and Hazel therefore
drank tea together for 46 weeks. If in two weeks they drank one pound of tea, in 46
weeks they will drink 46/2, which is equal to 23 lbs of tea. If one pound of tea is
$9.00, then 23 lbs of tea will cost 23x9, which is equal to $207.00
17. There were 63 balloons in each bag.
Ulrike could blow up a balloon in 5 seconds and tie it in 3 seconds and 5 plus 3 is 8.
Lars can blow up a balloon in 6 seconds and tie it in 4 seconds. And 6 plus 4 is 10.
Lars can blow up 6 balloons in 1 minute because 10 times 6 is 60 and there are 60
seconds in a minute. And Ulrike can blow up 7 and a half balloons in one minute. Lars
can blow up and tie 84 balloons in 14 minutes because 14 times 6 is 84. Ulrike can
blow up and tie 105 balloons in 14 minutes because 14 times 7 and a half is 105. We
used a table and added 15 for every two minutes for Ulrike. And Lars we put 12 for
every two minutes.
We then added 84 plus 105 to get 189. And then we used a calculator to divide 189
into three parts, which equaled 63.
18. 1. 30 clovers per minute. 2. 2 seconds per clover. Extra A. 9 weeks and 6 days, at
5:36pm , Extra B. 8,308 clovers per minute to finish by 6:00 pm.
4
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
Problem 1: First I calculated for how long Horton picked clovers. I found that out by
subtracting 6:56 from 12:00. That equaled 5:04. I converted that into minutes by
multiplying 5 hours x 60 minutes per hour, which equals 300 minutes. I added the
extra 4 minutes to 300 because that would give me the total number of minutes
Horton picked, which is 304. I took the total number of clovers picked, which was
9,005, and divided it by 304 because that would give me the number of clovers
Horton picked per minute. That equals 29.62171, which I rounded to 30 clovers per
minute, which is the answer.
Problem 2: If Horton picks 30 clovers per minute, then an equivalent statement
would be 30 clovers per 60 seconds. Then I divided 60 seconds by 30 clovers per 60
seconds to give me how many seconds he spent on each clover. The answer is 2
seconds.
Extra A: Since he found the speck on the 3 millionth clover, and he picks 30 clovers
per minute, I divided 3,000,000 by 30 to get 100,000 minutes. 100,000 minutes
divided by 60 gives me 1666 2/3 hours. 1666 2/3 hours divided by 24 is 69 days, 10
hours, and 40 minutes. So he would find the speck in 9 weeks and 6 days, at 5:36pm.
Extra B: First, I found out how many clovers Horton picked between noon and 6:00
pm. To find this out I subtracted the 9,005 he picked in the morning from the
3,000,000 he picked altogether. That gave me 2,990,995 clovers picked in the
afternoon. Then I figured out how much time he spent picking in the afternoon by
subtracting 6:00 pm from 12:00pm. That gave me a total of 6 hours spent picking in
the afternoon. I then divided the 2,990,995 clovers picked in the afternoon by the 6
hours he spent picking because that would give me the number of clovers that
needed to be picked per hour to achieve the goal. That answer was 498,499 clovers
picked per hour. To convert this to the number of clovers picked per minute, I
divided 498,499 by 60 because there are 60 minutes in an hour. That gave me a
picking rate of 8,308 clovers picked per minute. That means Horton would have to
pick 8,308 clovers per minute to finish by 6:00 pm
19. The tank would have been empty by 5:17 if you had not discovered the leak.
Step 1) The first thing I did was to figure out how many tablespoons are equal to one
gallon. To do this I started with the number of tablespoons in one cup (16 tbsp = 1
cup).
Step 2) Since I know that there are four cups in one quart I multiplied 16 x 4 which
equals 64, therefore I know that there are 64tbsp in 1qt, I also know that there are
4qt in one gallon. I then multiplied 64 x 4 and came up with there being 256 tbsp in 1
gallon.
Step 3) Next using the information I had collected I set up a ratio of tbsp to
seconds, 2:1 = 256:x, to solve the ratio I crossed multiplied and came up with x =
128sec. per gallon.
Step 4) Now I know that it takes 128 sec. for one gallon to leak out of the tank, so I
multiplied 128 x 30 =3840 (because we are told that there are 30 gallons in the
tank). Next I divided the 3840 by 60, so I can change the time from seconds to
5
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
minutes. I then concluded that it would take a total of 64 minutes to empty the tank
(or 1 hour and 4minutes).
Step 5) My final step was to add the 64 minutes to 4:13 which equals 5:17
Bonus: If the tank was leaking at a rate of 3 tbsp per sec. then it would be empty at
4:55:40.
To solve the bonus I set up another ratio using 3 tbsp per sec. rather than 2 tbsp
per sec. At this new rate the tank would empty in 42 min. and 40 sec. or 4:55:40.
6
Unit 5 – Rates, Ratios, and Proportions
Lesson 2 – Rates
Blue Handout
Bibliography Information
Teachers attempted to cite the sources for the problems included in this problem set. In some cases,
sources may not have been known.
Problems
Bibliography Information
16 - 19
The Math Forum @ Drexel
(http://mathforum.org/)
7