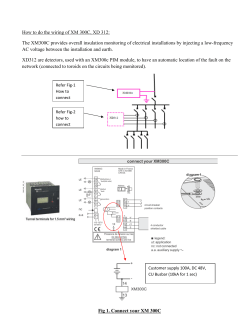
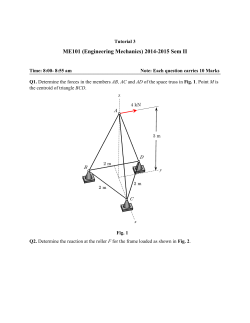
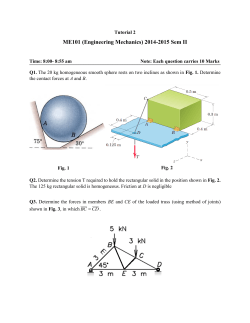
EE324 Lab 12 - Allison Thongvanh
Allison Thongvanh Section B Thursday 12:10 - 3PM Spring EE324 Lab 12 13 Lab 12 Thongvanh 1 Purpose In this lab we observe how the use of feedback influences the stability of an amplifier and what measures can be taken to improve this effect. To make said observations, we experiment with and manipulate the compensator network in Figure 1. Fig. 1 Feedback system with compensator network Lab Assignment We are given the Laplace transfer function of Figure 1 as A(s), Equation 1, and that L(s) is the function as shown in Equation 2. 10 5 A(s) = Eq. 1 (1+ 10−4 s)(1+ 10−6 s) L(s) = € R2 A(s) = R ⋅ A(s) R1 + R2 Eq. 2 First we use MatLab to verify the Bode plot of A(s) and L(s). Then we verify the phase margin and step-response of T(s), Equation 3. (See Appendix A2 for derivation of T(s)). € T(s) = A(s) A(s) = 10000 1+ A(s) ⋅ R 1+ A(s) 10000 + 90000 € Fig. 2 Bode plot of A(s) Fig. 3 Bode plot of L(s) Eq. 3 Lab 12 Thongvanh 2 Fig. 4 Gain and Phase Margins of T(s) (zoomed on margins on right) Fig. 5 Step Response of T(s) Now we improve the response using a lead compensator system. The improved system is shown in Figure 6. Fig. 6 Improved compensator network Lab 12 Thongvanh 3 Lastly we find a value for the capacitor in the improved compensator network. To do so we find the transfer function for the network itself (Equation 4), play with numbers for the capacitor value, and observe the values' effects on L(s). R2 R2 R2 Eq. 4 R( s) = = = 1 R1sC + 1 Z + R 2 R1 || + R2 + R2 sC R1 • R1 = 9k Ω , R2 = 1k Ω , C = 1pF Transfer functions: € 9e11 L(s)=-----------------------------------90 s^3 + 9e16 s^2 + 9.09e12 s + 9e06 9e06 s^3 + 9e21 s^2 + 9.09e17 s + 9e11 T(s)=-------------------------------------------------------------------9e11 s^5 + 9e26 s^4 + 1.818e23 s^3 + 9.009e21 s^2 + 9.09e17 s + 9e11 Fig. 6 Bode Plot of L(s) Fig. 7 Step Response of T(s) Fig. 8 Bode Plot of T(s) Lab 12 • Thongvanh 4 R1 = 9k Ω , R2 = 1k Ω , C = 5pF Transfer functions: 9e11 L(s)=------------------------------------450 s^3 + 9e16 s^2 + 9.09e12 s + 9e06 4.5e07 s^3 + 9e21 s^2 + 9.09e17 s + 9e11 T(s)=---------------------------------------------------------------------4.5e12 s^5 + 9e26 s^4 + 1.818e23 s^3 + 9.009e21 s^2 + 9.09e17 s + 9e11 Fig. 9 Bode Plot of L(s) Fig. 10 Bode Plot of T(s) Fig. 11 Step Response of T(s) Lab 12 • Thongvanh 5 R1 = 9k Ω , R2 = 1k Ω , C = 10pF Transfer functions: 9e11 L(s)=------------------------------------900 s^3 + 9e16 s^2 + 9.09e12 s + 9e06 9e07 s^3 + 9e21 s^2 + 9.09e17 s + 9e11 T(s)=-------------------------------------------------------------------9e12 s^5 + 9e26 s^4 + 1.818e23 s^3 + 9.009e21 s^2 + 9.09e17 s + 9e11 Fig. 12 Bode Plot of L(s) Fig. 13 Bode Plot of T(s) Fig. 14 Step Response of T(s) Lab 12 • Thongvanh 6 R1 = 9k Ω , R2 = 1k Ω , C = 15pF Transfer functions: 9e11 L(s)=-------------------------------------1350 s^3 + 9e16 s^2 + 9.09e12 s + 9e06 1.35e08 s^3 + 9e21 s^2 + 9.09e17 s + 9e11 T(s)=----------------------------------------------------------------------1.35e13 s^5 + 9e26 s^4 + 1.818e23 s^3 + 9.009e21 s^2 + 9.09e17 s + 9e11 Fig. 15 Bode Plot of L(s) Fig. 16 Bode Plot of T(s) Fig. 17 Step Response of T(s) Conclusion The purpose of this lab was to observe how the use of feedback influences the stability of an amplifier and what measures can be taken to improve this effect. We observe changes in phase of L(s) when changing the capacitor in the compensator network. I would choose the 10 pF capacitor. Lab 12 Thongvanh 7 Appendix A1: Various A(s), L(s), and T(s) plots >> >> >> >> >> >> >> >> >> >> >> r1=9000; r2=1000; c=1e-12; z=tf([r1*c 1],[r1]); RS=r2/(z+r2); AS=tf([0 0 0 0 0 1e5],[10000000000 1010000 1]); LS1=AS*RS TS1=AS/(1+LS1); bode(LS1) margin(TS1) step(TS1) %Repeat the same process for varied capacitor (c) values. A2: Gain = 10 calculation Given R=R2/(R1+R2) Vo(s) = A(s)(Vp(s)−Vn(s))=A(s)(Vp(s)−RVo(s)) Therefore, Vo(s) A(s) ----- = ---------Vp(s) 1+A(s)*R From here, manipulate values in R so that gain is equal to 10.
© Copyright 2026