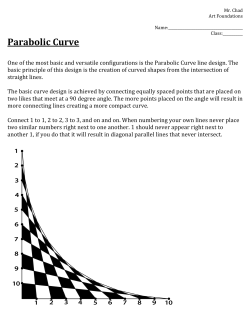
5/5/2015
Sections 6-1 and 6-2
Review and Preview
and
The Standard Normal Distribution
NORMAL DISTRIBUTIONS
Ifacontinuousrandomvariable
hasadistributionwithagraph
thatissymmetricandbell‐
shapedandcanbedescribedby
theequation
2
wesaythatithasanormal
distribution.
REMARK
WewillNOT needtousetheformulaonthe
previousslideinourwork.However,itdoes
showusoneimportantfactaboutnormal
distributions:
Anyparticularnormaldistributionis
determinedbytwoparameters:
themean,μ,and
thestandarddeviation,σ.
1
5/5/2015
HEIGHTS OF WOMEN AND MEN
Women:
µ = 63.8
 = 2.5
Men:
µ = 69.4
 = 2.8
63.8
69.4
Height (inches)
UNIFORM DISTRIBUTIONS
Acontinuousrandomvariablehasauniform
distribution ifitsvaluesarespreadevenly
overtherangeofpossibilities.Thegraphofa
uniformdistributionresultsinarectangular
shape.
EXAMPLE
Supposethatafriendofyoursisalwayslate.
Lettherandomvariable representthetime
fromwhenyouaresupposetomeetyourfriend
untilhearrives.Yourfriendcouldbeontime
(
0)orupto10minuteslate(
10)with
allpossiblevaluesequallylikely.
Thisisanexampleofauniformdistribution
anditsgraphisonthenextslide.
2
5/5/2015
0.1
1
0
0.0
10.0
Numberofminuteslate
DENSITY CURVES
Adensitycurve (orprobabilitydensity
function)isagraphofacontinuous
probabilitydistribution.Itmust satisfythe
followingproperties:
1. Thetotalareaunderthecurve
mustequal1.
2. Everypointonthecurvemust
haveaverticalheightthatis0or
greater.(Thatis,thecurvecannot
fallbelowthe ‐axis.)
IMPORTANT CONCEPT
Becausethetotalareaunder
thedensitycurveisequalto1,
thereisacorrespondence
betweenarea andprobability.
3
5/5/2015
EXAMPLE
Supposethatafriendofyoursisalwayslate.
Lettherandomvariable representthetime
fromwhenyouaresupposetomeetyour
frienduntilhearrives.Yourfriendcouldbeon
time(
0)orupto10minuteslate(
10)
withallpossiblevaluesequallylikely.Findthe
probabilitythatyourfriendwillbemorethan
7minuteslate.
THE STANDARD NORMAL
DISTRIBUTION
Thestandardnormaldistribution isanormal
probabilitydistributionthathasamean
0
andastandarddeviation
1,andthetotal
areaunderthecurveisequalto1.
COMPUTING PROBABILITIES
FOR THE STANDARD NORMAL
DISTRIBUTION
Wewillbecomputingprobabilitiesforthe
standardnormaldistributionusing:
1. TableA‐2locatedinsidethebackcoverof
thetext,theFormulasandTables insert
card,andAppendixA(pp.584‐585).
2. TheTI‐83/84calculator.
4
5/5/2015
COMMENTS ON TABLE A-2
1. TableA‐2isdesignedonlyforthe
standard normaldistribution
2. TableA‐2isontwopageswithonepage
fornegative z scoresandtheotherpage
forpositive z scores.
3. Eachvalueinthebodyofthetableisa
cumulativeareafromtheleft uptoa
verticalboundaryforaspecificz score.
COMMENTS (CONCLUDED)
4. Whenworkingwithagraph,avoidconfusion
betweenz scoresandareas.
z score: Distance alongthehorizontal
scaleofthestandardnormaldistribution;
refertotheleftmostcolumnandtoprow
ofTableA‐2.
Area: Region underthecurve;referto
thevaluesinthebodyoftheTableA‐2.
5. Thepartofthezscoredenotinghundredths
isfoundacrossthetoprowofTableA‐2.
NOTATION
denotestheprobabilitythat
thez scoreisbetween and
.
denotestheprobabilitythat
thez scoreisgreaterthan .
denotestheprobabilitythat
thez scoreislessthan .
5
5/5/2015
COMPUTING PROBABILITIES
USING TABLE A-2
1. Drawabell‐shapedcurvecorresponding
totheareayouaretryingtofind.Label
thez score(s).
2. Lookupthez socre(s)inTableA‐2.
3. Performanynecessarysubtractions.
FINDING THE AREA BETWEEN
TWO z SCORES
Tofind
,theareabetween and :
1. Findthecumulativearealessthan ;that
is,find
.
2. Findthecumulativearealessthan ;that
.
is,find
3. Theareabetween and is
.
FINDING PROBABILITIES
(AREAS) USING THE TI-83/84
Tofindtheareabetweentwoz scores,press
2ndVARS (forDIST)andselect2:normalcdf(.
Thenenterthetwoz scoresseparatedbya
comma.
Tofindtheareabetween−1.33and0.95,your
calculatordisplayshouldlooklike:
normalcdf(−1.33,0.95)
6
5/5/2015
FINDING PROBABILITIES (AREAS)
USING THE TI-84 NEW OS
Tofindtheareabetweentwoz scores,press
2ndVARS (forDIST)andselect2:normalcdf(.Then
enterthetwoz scoresseparatedbyacomma.
Tofindthearea
between−1.33and
0.95,yourcalculator
displayshouldlook
like:
NOTES ON USING TI-83/84 TO
COMPUTE PROBABILITIES
• TocomputeP(z <a),use
normalcdf(−1E99,a)
• TocomputeP(z >a),use
normalcdf(a,1E99)
PROCDURE FOR FINDING A z
SCORE FROM A KNOWN AREA
USING TABLE A-2
1. Drawabell‐shapedcurveandidentifythe
regionthatcorrespondstothegiven
probability.Ifthatregionisnota
cumulativeregionfromtheleft,work
insteadwithaknownregionthatis
cumulativefromtheleft.
2. Usingthecumulativeareafromtheleft
locatetheclosestprobabilityinthebody
ofTableA‐2andidentifythe
correspondingz score.
7
5/5/2015
FINDING A z SCORE
CORRESPONDING TO A KNOWN
AREA USING THE TI-83/84
Tofindthez scorecorrespondingtoaknown
area,press2ndVARS (forDIST)andselect
3:invNorm(.Thenenterthetotalareatothe
leftofthevalue.
Tofindthez scorecorrespondingto0.6554,a
cumulativeareatotheleft,yourcalculator
displayshouldlooklike:
invNorm(.6554)
FINDING A z SCORE FROM
AN AREA ON TI-84 NEW OS
Tofindthez scorecorrespondingtoaknownarea,
press2ndVARS (forDIST)andselect3:invNorm(.
Thenenterthetotalareatotheleftofthevalue.
Tofindthez score
correspondingto
0.6554,acumulative
areatotheleft,your
calculatordisplay
shouldlooklike:
CRITICAL VALUES
Foranormaldistribution,acriticalvalue isa
z scoreontheborderlineseparatingthez
scoresthatarelikelytooccurfromthosethat
areunlikelytooccur.
NOTATION:Theexpression denotesthe
z scorewithanareaof toitsright.( isthe
Greeklower‐caseletteralpha.)
8