1. No category

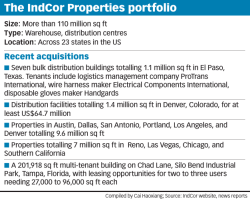
An investigation of the gains from commitment in
monetary policy
Ernst Schaumburg and Andrea Tambalotti
JME
Two possible assumptions when modeling optimal policy:
I
an infinitely lived policy maker can credibly commit to a policy
(function) forever
I
policy maker can not credibly commit at all
the assumption of commitment usually leads to time inconsistent
policies.
This Paper
This paper tries to analyze ’intermediate’ cases where a policy maker
can commit to a policy rule but is only in power for a random number
of periods.
I
draws of a Bernoulli random variable ηt indicate whether or not a
new policy maker is in power.
I
α: probability of policy maker being replaced next period ’measure of credibility’
I 1:
α
I τj :
I
average duration of regime
time period policy maker j comes into power
∆τj = τj+1 − τj − 1
The Private Sector
xt = Et xt+1 − σ(it − Et πt+1 − rte )
(1)
πt = κxt + βEt πt+1 + ut
(2)
Lt = πt2 + λx (xt − x∗ )2
(3)
It = {rse , us , ηs }s≤t
(4)
Optimal Policy Problem
Assume for now ut iid


∆τj
X
V(uτj ) = max min Eτj 
β k Lτj +k + β ∆τj +1 V(uτj+1 )
φk+1 xk ,πk
(5)
k=0
φ τj = 0
(6)
Lt = Lt + 2φt+1 (−πt + κxt + βEt πt+1 + ut )
(7)
Guess solution for π:
πt+1 = h0 + h1 ut+1 + h2 φt+1
(8)
This implies:
Et πt+1 = (1 − α)Et0 πt+1 + αEt1 πt+1 = (1 − α)Et0 πt+1 + αh0
(9)
where
Eti πt+1 = Et [πt + 1|ηt+1 = i]
(10)
some of the FONC’s:
λx (xt − x∗ ) + κφt+1 = 0
(11)
πt − φt+1 + φt = 0
(12)
This yields
λx
(xt − x∗ )
κ
κµ1 ∗
h0 =
x
1 − βµ1
φt+1 =
(13)
(14)
If no regime change ever occurred xt would converge to
¯x = −
αβµ1 ∗
x
1 − βµ1
(15)
˜xt = ¯xt − x∗
(16)
output gap dynamics within regime:
˜xt = µt+1
1
t
κ X s
1 − (1 − α)βµ1 ∗
x − µ1
µ1 ut−s
1 − βµ1
λx
(17)
s=0
πt =
κ
˜xt + ut
1 − (1 − α)βµ1
(18)
Calibration
IR Definitions