1. hobbies and interests
2. games
3. board games and puzzles

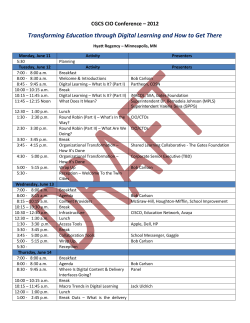
How to pair with a human
Stefan Dziembowski
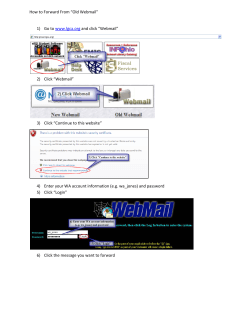
Department of Computer Science
University of Rome
La Sapienza
Abstract. We introduce a protocol, that we call Human Key Agreement, that allows pairs of
humans to establish a key in a (seemingly hopeless) case where no public-key infrastructure is
available, the users do not share any common secret, and have never been connected by any
physically-secure channel. Our key agreement scheme, while vulnerable to the human-in-themiddle attacks, is secure against any malicious machine-in-the middle. The only assumption
that we make is that the attacker is a machine that is not able to break the Captcha puzzles
(introduced by von Ahn et al., EUROCRYPT 2003).
Our main tool is a primitive that we call a Simultaneous Turing Test, which is a protocol that
allows two users to verify if they are both human, in such a way that if one of them is not a
human, then he does not learn whether the other one is human, or not.
To construct this tool we use a Universally-Composable Password Authenticated Key Agreement
of Canetti et al. (EUROCRYPT 2005).
1
Introduction
One of the main reasons why digital crime is so difficult to combat is the fact that the attacks on digital
devices are usually very easy to automatize and repeat for a large number of times. This makes the
design of secure digital systems a completely different discipline than the design of physically-secure
systems. Just observe that a physical attack on a bank that has probability 0.1% of succeeding may
be infeasible, while, an electronic attack on a banking system that has the same probability of success
may be feasible and profitable for the attacker.
The observation that certain types of malicious behavior are profitable only if they can be performed
automatically and efficiently led to a construction of schemes where at some point one of the users
has to prove that he is a human. This type of a “proof of being a human” was first proposed in [27],
then independently discovered by [24], and finally formalized, and put in a general framework in [36],
where it was given a name Completely Automated Public Turing test to tell Computers and Humans
Apart (Captcha). In short, a Captcha scheme is a puzzle that is easy to solve by a human and hard
to solve by a machine. The most common Captchas are computer-generated images containing a short
string of characters written in such a way that they are unreadable for a computer, and still effortlessly
readable by a human (cf. Fig. 1). Other Captchas that were proposed are based on: recognizing gender
of a person on an image [27], understanding facial expression on an image [27], speech recognition [27],
recognizing animal pictures [36], etc.
So far, Captcha schemes were mostly used as a method for preventing attacks in which the adversary
simply floods the victim with a large number of unwanted requests. Examples of these include email
spamming and automated posting to blogs, forums, on-line polls, wikis, etc. [27, 36]. Captchas are
also used as a for thwarting the dictionary attacks on the password-based systems. In particular, [12]
proposed to use Captcha for protecting local storage from such attacks. Also, some manufacturers of
Fig. 1. An example of a Captcha from Google.
home wifi routers recently started to use Captcha to prevent malicious software from getting access to
their machines by simply guessing a password [31].
In this paper we propose a new application of the Captcha schemes. We show how Captchas can
be used to construct a session key agreement between two humans that are connected by an insecure
link. Our protocol, that we call a Human Key Agreement works in a (seemingly hopeless) case where
no public-key infrastructure is available, and the users do not share any common secret, have never
been connected by any physically-secure channel and do not even know each other personally (so they
cannot, e.g., recognize each other’s voice). The only assumption that we make is that the attacker is
a machine that is not able to break the Captchas generated by the users.
1.1
Related work
Captcha Some work on Captchas was already described in Sect. 1. Both designing and breaking
Captcha schemes is subject of intensive and active research. One of the interesting new research ideas
in this field is the reCaptcha project [37], where the users solving Captchas are helping to digitize old
books by deciphering scanned words on which the OCR methods failed. In this case Captcha consists of
two images, (a) one that the creator of Captcha can solve himself (this is needed to verify the answer),
and (b) one that is unreadable for him. The key point here is that the user who solves the Captcha
does not know which image is (a) and which is (b), and hence he has to provide a solution for both.
Typically, the attacks on Captcha use the artificial intelligence methods (see e.g. [21]). An interesting
exception is a so-called a pornography attack, where the the Captcha puzzles are forwarded to a
pornographic web-site, and the web-site users have to solve the Captcha before being allowed to
view the web-site contents [38]. For more information and references on Captcha see e.g. the Captcha
web-site [34], or the wikipedia article [40].
Key agreement protocols Key agreement protocols were introduced by Diffie and Hellman in their
seminal paper [14]. Informally, a key agreement protocol is a scheme that allows two parties that
initially do not share any secret to agree on a common key. The protocol of [14] is secure only against
an eavesdropping adversary, i.e. an adversary that can passively listen to the messages exchanged
between the parties, and is not secure against a more powerful active adversary that fully controls the
transmission (by modifying, coping, fabricating or destroying the messages). Such an active adversary
is also called a man-in-the middle. Subsequently, several methods of protecting against the active
attacks were proposed. A common one is to add message authentication to a passively-secure key
agreement scheme. For example if the parties already share a common key K, they can authenticate
their messages using Message Authentication Codes (see Sect. 3.1 for a definition). It may seem that
the assumption that the parties from the beginning share a key trivializes the problem. The main
point, however, is that such schemes allow to generate several fresh session keys from one long-term
key K. An advantage of this method is that it provides forward-security [15, 18, 2], i.e. even if at some
point the key K leaks to the adversary, the session keys generated in the past remain secret.
Other popular methods for authenticated key agreement are based on the public-key cryptography,
or a trusted third party (for more on this, and for a general introduction to the area of key agreement
see e.g. [6]). The drawback of the PKI approach is that it relays on a public-key infrastructure, that is
usually non-trivial to set-up [16]. Using the trusted third party is often impractical, since it requires
the parties to be connected to a party whom they both trust.
Some protocols are also based on the assumption that the agreeing parties share a common password, which may not be chosen uniformly at random, but has to be hard to guess for the adversary
(we discuss it in more detail in Sect. 4). Yet another method, called short string comparison, assumes
that the agreeing parties, after the protocol is completed, are able to securely compare, via a trusted
channel if two short strings are equal [35, 29, 23, 9]. Such a comparison allows the parties to detect if
the adversary performed the man-in-the middle attack, by verifying if both parties have the same view
on the set of messages that were exchanged.
Secure pairing schemes Secure device pairing is a term used in the systems security community,
referring to protocols whose goal is to establish a secret key between two electronic gadgets (mobile
phones, PCs, routers, headsets, cameras and media players, etc.), usually connected with a wireless
link. Hence, the meaning is similar to the term key agreement described above, and in fact some of
the key agreement protocols can be directly used for pairing. The main difference is that the pairing
protocols do not assume any shared secrets, trusted parties, or PKI. Moreover, the interfaces of the
devices are often so constraint that they do not even permit the use of password protocols (since, e.g.,
they lack a keyboard or a screen). These protocols usually rely on a human user that is available to
assist the pairing.
The first pairing pairing protocol [33] was based on an assumption that a user can actually connect
the devices with a secure physical link. Later, several other schemes were proposed. Several of them
rely on a so-called “out-of-band” (OOB) channels, which are channels whose security can be verified
by the user. For example [3] uses an infrared channel as OOB, and [32] uses human body as the
communication medium. Some protocols use essentially the “short string comparison” method. For
example the protocol [30] requires the user to verify if the images (that are a graphical representations
of the “short strings”) displayed on both devices are the same. The protocol used in the Zfone, a secure
VoIP system (see [41]), requires the users to read out to each other short strings, and to compare them
(another example of such a protocol is [42]). The security of this system of course relies on the fact
that the users can recognize each other’s voice. For more examples of the pairing protocols see e.g.
[22].
2
Our contribution: Human Key Agreement
In this section we describe the Human Key Agreement protocol. Informally speaking that, our protocol,
while vulnerable to the “man-in-the middle” attacks, is secure against the “machine-in-the-middle”
attacks (i.e.: an attack in which the adversary in not a human). Moreover, the protocol will be designed
in such a way that using a human-in-middle attack, will be very expensive, since it will require the
adversary to use humans to constantly monitor the network, solving a large number of Captcha puzzles.
Consider a decentralized protocol for remote communication between the humans. For example,
think of an internet instant messaging system, like XMPP1 , or in general, any system where pairs of
humans need to establish secure connection. How can the users of such a protocol establish session keys
in a way that is secure against the man-in-the-middle attacks, when the the Public-Key Infrastructure
is not available? None of the methods described in Sect. 1.1 seems to be applicable in this case. It
is usually infeasible for the users to meet in person in order to establish a shared secret password.
Sometimes they do not know each other well, so they cannot recognize each other’s voice, and hence
they cannot use the “short string comparison” method used in the VoIP protocols [41, 42] (another
reason may be that the voice link may simply not be available). Relying on a trusted server may also be
a bad idea, as reported recently in the media [39]. Therefore, the adversary that controls the network
can freely monitor, store and analyze all the messages that are transmitted by the users (as described
in [39]).
Our Human Key Agreement permits the users to significantly increase security of their communication in this situation. The security of our protocol is based on the difficulty of solving the Captcha
puzzles by a machine. More precisely the key established between each pair of participants will remain
secret assuming that the adversary did not solve the Captcha puzzles that the users generated during
the execution of the protocol. In addition, our protocol will be forward-secure, which means that, in
order to break the security, the adversary will have to solve the Captcha puzzles during the execution
of the protocol (solving the Captchas after the protocol is completed does not help him). Therefore
the adversary will have to employ a significant amount of human power in order to decrypt users
communication. Although, of course, this does not prevent him from targeting a concrete user, or a
pair of users (if he is willing to spend some of his human time), at least it makes it very expensive
to monitor and analyze the whole communication in the network. In some sense this is similar to the
method based on voice recognition [41], since also there a very determined adversary may actually able
to break the security, by using a voice mimic attack [42].
The details of the model are a little bit tricky, and we start with presenting them in a very
informal way. Consider two parties, Alice (A) and Bob (B), that want to establish a secure connection.
Intuitively, our protocol should satisfy the following requirements:
Requirement 1 If the adversary is passive the protocol is completely secure, even against a humanadversary.
Requirement 2 If the adversary is performing a machine-in-the middle attack then this attack will
be detected by the users.
Therefore, of course, an active machine-adversary will always be able to prevent the parties from
establishing a secure key, but he will not be able to convince the players that the key is secure, while
it is not.
It is easy to observe that in order to satisfy Req. 1 both users themselves have to use the fact that
their are humans, and demonstrate, during the execution of the protocol, their ability to solve the
Captcha puzzles. This is because otherwise a machine-attacker would be completely indistinguishable
from the honest users. On the other hand, solving a Captcha each time the protocol is executed would
be very cumbersome. Therefore the protocol will have two modes: a secure one (during which the users
1
XMPP stands for Extensible Messaging and Presence Protocol. It was formerly named Jabber. For more on
XMPP see e.g. a wikipedia article http://en.wikipedia.org/wiki/Extensible_Messaging_and_Presence_
Protocol
have to solve the Captcha puzzles) and both Req. 1 and 2 hold, and a normal one, where only Req. 1
holds.
The secure mode will only be activated if the users need to transmit some secret information, and
otherwise they will use the normal mode. More precisely, each user P ∈ {A, B} will be able to decide
if he wants to establish a secure connection, or not, by setting his flag humanP := 1, or humanP := 0,
resp. The secure mode will be used only if humanA ∧ humanB = 1.
Described this way, it may look like the protocol could actually deteriorate users’ security, as the
fact that one of the users wants to establish a secure connection could be a signal to the adversary that
the user has some secret to hide (and in this case he could quickly call a human to help him solving
the Captcha). Thus we introduce the third security condition:
Requirement 3 A machine-adversary is not able to learn the values of humanA and humanB . Moreover the values of humanA and humanB are forward-secret in a sense, that the adversary, in order
to learn those values, needs to solve the Captcha puzzles during the execution of the protocol.
The reason why the users may be interested in forward-secrecy of humanP is that the fact that some
pair of users used the secure mode, could draw the attention of the adversary to them, and hence he
could use a human-attacker against them next time when they execute the key-agreement protocol.
For this reason, the users should be advised to always encrypt their communication with the secret
key that they established, no matter if they are in the secure mode or not (since otherwise they would
reveal the values to the adversary).
Req. 3 implies that the computation of humanA ∧ humanB has to be done in a “covert” way.
In particular the parties cannot just send to each other their values humanA and humanB , and in
general none of them can send it to anyone who did not first prove to him that he is human (since the
communication is not authenticated, and one never knows to him he is really talking).
A natural idea for a solution is as follows: let Alice reveal to Bob that humanA = 1 only if Bob
proves to her that he is human. If we apply this in a naive way, then of course we enter a loop, since in
turn Bob will be willing to prove this only if Alice proves to him that she is human. Fortunately, it turns
out that we can construct a protocol in which Alice and Bob prove to each other that they are human
simultaneously, i.e. they will prove to each other that they are human, in such a way that if one of them
is not a human, he will not learn if the other party is a human or not. We call this a Simultaneous
Turing Test2 Moreover, also this proof will be forward-secure in the sense, that an adversary that
solves the Captcha puzzles after the protocol was completed, will not have any information about the
inputs humanA and humanB . The main tool that we use is called Universally-Composable Password
Based-Key Exchange (see Sect. 3.4 for more on this).
While from this description it may seem that our protocol is very complicated, the good news is
that in fact from the user point of view the execution of the protocol is quite simple. In particular,
each of the users will need to solve the Captcha puzzle only once, during the Simultaneous Turing
Test, and the rest of the protocol will be fully automatic. Our protocol may be implemented in the
following way. When the users start communicating, each of them has an option to choose a “secure
connection” (by pressing some button in his interface, say). In this case his client shows him a Captcha
2
In some sense this is similar in spirit to the problem of secure two-party computation of a conjunction. Recall
that a secure evaluation of a two-party function f : {0, 1}∗ × {0, 1}∗ → {0, 1}∗ is a protocol that allows Alice
and Bob to learn f (xAlice , xBob ) without revealing to each other their respective inputs xAlice and xBob . This
means in particular that if f is a conjunction of two bits then the following security guarantee holds for both
P ∈ {Alice, Bob}: if xP = 0 then P will not know if the input of the other party was 0 or 1. See e.g. [13] for
an introduction to this area.
sent from the other user, and the user has 1 minute, say, to solve it. If also the other user solved the
Captcha then the client displays an information “secure connection established”, and otherwise it says
“insecure connection”. The user of course does not know if it is because the other user has not chosen
“secure connection”, or because the adversary interfered in the transmission, but this is unavoidable
in our model.
The option to switch to the secure mode may be permanently available for the users (i.e. the clients
can, invisibly for the users, execute the key agrement scheme every minute, say). Of course, the users
should not explicitly say (over an insecure link) that they want to establish a secure connection, since
it would violate Req. 3. The user can, however, indicate it in some non-explicit way, hoping that the
other player will understand it, but an inattentive adversary will not.
One of the possible weaknesses of this model is that it does not distinguish between a user that
makes an error while solving Captcha, and an adversary. Fortunately, we have an extended version of
the protocol (see Sect. 4.5), where the user has a right to a couple of tries when solving Captcha.
3
Tools
3.1
Message Authentication Codes
Message Authentication Codes (MAC s) is a tool for guaranteeing integrity of communication between
two paries that share a key. An introduction to MACs and a complete security definition can be found,
e.g., in [19]. We will use a following definition of MACs. MAC is a pair of algorithms (Tag, Vrfy),
such that Tag takes as an input a random secret key S ∈ {0, 1}k and a message M ∈ {0, 1}∗ . It
outputs an authentication tag Tag S (M ). We require that always Vrfy S (M, Tag S (M )) = 1. It is secure
against chosen-message attack if any polynomial probabilistic time adversary (taking as input 1k ) has
negligible3 (in k) chances of producing a pair (M, T ) such that Vrfy S (M, T ) = 1, even after seeing an
arbitrary number of pairs
(M1 , Tag S (M1 )), (M2 , Tag S (M2 )) . . .
(where M 6∈ {M1 , M2 , . . .)) and even when M1 , M2 , . . . were adaptively chosen by the adversary.
In our construction we will use a special type of MACs, that have the following non-standard
feature: informally, it should be infeasible to discover if two tags were computed with the same key.
More precisely, we require that for S0 , S1 ∈ {0, 1}k chosen uniformly at random, and for any M0 6= M1
no polynomial-time adversary that knows Tag S0 (M0 ) can distinguish between Tag S0 (M1 ) (i.e. M1
encrypted with the same key) and Tag S1 (M1 ) (i.e. M1 encrypted with a fresh key). This can be
formalized as follows: for every polynomial-time machine A and every M0 and M1 we have that
|P A(Tag S0 (M0 ), Tag S0 (M1 ) = 1) −P A(Tag S0 (M0 ), Tag S1 (M1 ) = 1) |
(1)
is negligible.
The standard definition of MACs does not guarantee this. This is because the definition of MACs
does not require that no information about the key leaks to the adversary. For example, it may be
possible that a MAC is secure, but the first 10 bits of S can be computed from Tag S (M ) (and hence
it can be easily checked if two tags were computed with the same key). Luckily, concrete examples
of MACs satisfy this extended definition. One example is the standard construction of a MAC from
3
A f : N → R function is negligible in k if for every c ≥ 1 there exists k0 such that for every k ≥ k0 we have
|f (k)| ≤ k−c .
a pseudorandom function (cf. e.g. [19], Sect. 4.4). Recall, that a pseudorandom function (which is
essentially the same as a block-cipher) is a function f that takes as input some key S, and a (fixedlength) block M and outputs a ciphertext C = fS (M ) of the same length. Informally speaking, the
security of the pseudorandom functions is defined as follows: for every sequence of blocks M1 , . . . , Mt
the string fS (M1 ), . . . , fS (Mt ) should be indistinguishable from random (even is the blocks M1 , . . . , Mt
are chosen adaptively by the adversary). It is easy to see that a function Tag prf
S (M ) = fS (M ) (with
Vrfy prf defined in a straightforward way) is a secure MAC that works on messages of fixed length. It
can be extended to work on messages of arbitrary length by first hashing a message with a collision,H
resistant hash function H, and then applying f , i.e. setting Tag prf
(M ) := fS (H(M )) (this method
S
is called hash-and-authenticate, cf. [19]).
The reason why for any polynomial-time A the scheme Tag prf satisfies (1) is that, from the defprf
prf
prf
inition of a pseudorandom function, both Tag prf
S0 (M0 ), Tag S0 (M1 ) and Tag S0 (M0 ), Tag S1 (M1 ) are
indistinguishable from random strings, and hence, obviously, they are indistinguishable from each
other. The same holds for Tag prf ,H .
3.2
Key Agreement
Key Agreement is a scheme that allows two parties, Alice and Bob, that initially share no secret, to
establish a common key. For simplicity, in this paper we restrict ourselves to one-round key agreement
protocols. Hence, for us a key agreement protocol is a triple of randomized interactive algorithms
(KAAlice , KABob , KAKey ). Let rAlice and rBob denote the respective random inputs of the players. In
the first step each algorithm P ∈ {Alice, Bob} sends to the other one a message mP = KAP (rP ).
Then, Alice calculates her output KAlice = KAKey (rAlice , mBob ) and Bob calculates his output KBob =
KAKey (rBob , mAlice ). We require that always KAlice = KBob . Security of (Alice, Bob) is defined in the
following way: for any polynomial time adversary that can see mAlice and mBob the key KAlice should
be indistinguishable from a random string of the same length. Of course, if the adversary is active,
then he can cause KAlice 6= KBob , or KP = error (for P ∈ {Alice, Bob}).
An example of a key agreement protocol is the protocol of Diffie and Hellman [14]. Let G be a
cyclic group, and let g be its generator. The protocol works as follows: each user P selects a random
exponent rP ∈ Z|G| , calculates mP := g rP and sends it to the other player. Then, each player calculates
K := (mP )rP . The protocol is correct, since (g rAlice )rBob = (g rBob )rAlice . The protocol is secure under a
so-called Decisional Diffie-Hellman Assumption in (G, g). See, e.g., [19] for more on this.
Authenticated Key Agreement (AKA) is a protocol between Alice and Bob that share a common
key K that allows them to generate a fresh session key. It can be constructed from the Key Agreement
Scheme described, by asking both users to authenticated their messages with a MAC (using the key
K). In our construction we will need a stronger version of this notion, that we call a Covert-AKA.
This is described below.
3.3
Covert-AKA
As a building-block for our main construction we introduce a scheme that we call Covert-AKA. It is
a protocol between Alice and Bob. The players have as input two keys sk A and skB . The protocol is
executed either with sk A = sk B (this is called the “equal keys” case), or with sk A independent from
sk B (this is called the “independent keys” case). The properties of the protocol are as follows. If the
adversary is passive, then
– in the “equal keys” case both parties output the same output: (secure, K),
– in the “independent keys” case both parties output (normal, K).
If the adversary is active then
– in the “equal keys” case he can cause each party (independently) to output (normal, K 0 ) (for some
K 0 , that can be different for both parties), or error
– in the “independent keys” case he can cause each party (independently) to output error .
The security conditions are as follows: (1) no polynomial-time adversary that attacks the protocol (even
actively) can distinguish between the “equal keys” and “independent keys” case, and (2) whenever one
of the parties outputs (secure, K), the key K is indistinguishable from random, for a polynomial-time
adversary.
Covert-AKA can be implemented in a similar way to the normal AKA, namely both players execute
a passively secure key agreement, authenticating their messages in with the keys sk A and sk B , resp.
The complete protocol is presented on Fig. 2.
Obviously, if sk A = sk B then the players just executed a normal authenticated key agreement,
and hence whenever the adversary tampers with the messages he can cause the parties to output
(normal, K 0 ) (by tampering just with the tag), or error (by, e.g., destroying the whole message). If
the keys are independent then obviously the verification of the tag will fail.4 Therefore the adversary
cannot force any parties to output secure. Moreover, if he is passive, then both parties will always
output (normal, K).
Observe, that if the players use a standard MAC scheme for authentication, then the adversary
that observes the transcript can in principle see if the keys are equal or independent, since, as explained
in Sect. 3.1 a MAC does not even need to hide the entire key. Hence, we use Tag prf constructed in
Sect. 3.1, that has exactly the property that the adversary, after seeing the messages mAlice and mBob ,
and the Tags on them, cannot distinguish (with a non-negligible advantage) if they were authenticated
with the same key, or two independent keys.
3.4
Universally-Composable Password Authenticated Key Exchange
As briefly mentioned in Sect. 1.1 there exist key-agreement protocols, where it is enough that the users
share a password. Such schemes, introduced in [5], are called Password Authenticated Key Exchange
protocols. The main difference between a password, and a cryptographic key is that the latter is
usually assumed to have a unform distribution over some set {0, 1}m , and the distribution of the
former can be very far from uniform over {0, 1}m , e.g., it can be known to the adversary that the
password is a word from a dictionary. It is particularly important that such schemes offer protection
against the off-line password guessing attacks, i.e. the attacks, where the adversary can perform an
exhaustive search for a correct password, after he saw the transcript of the communication. The design
of such schemes attracted a considerable interest [4, 7, 26, 17, 28, 20, 8] during the last two decades, and
has proven to be a challenging task. It has even been non-trivial to come up with the right security
definitions. For example, most of the definitions made an unrealistic assumption that the passwords
are chosen according to some pre-determined distribution, and that the passwords between different
pairs of parties are chosen independently.
In this paper we will use a very strong version of such a protocol, called Universally-Composable
Password Authenticated Key Exchange (UC PAK), defined and constructed in [11]. Its definition follows
4
Actually, here we really need the assumption that the keys are independent, since otherwise the adversary
could in principle be able to exploit the correlations between the keys, and launch a related-key attack.
Alice
Bob
mAlice := KAAlice (rAlice )
tAlice := Tag prf
sk (Alice, mAlice )
mBob := KABob (rBob )
tBob := Tag prf
sk (Bob, mBob )
((Alice,mAlice ),tAlice )
−
−−−−−−−−−−−−
−→
((Bob,mBob ),tBob )
←−−−−−−−−−−
if KAKey (rBob , mAlice ) = error
then output error
if KAKey (rAlice , mBob ) = error
then output error
otherwise:
otherwise:
if
Vrfy prf
sk
((Bob, mBob ), tBob ) = 1
then output
(secure, KAKey (rAlice , mBob ))
otherwise output
(normal, KAKey (rAlice , mBob )).
if
Vrfy prf
sk
((Alice, mAlice ), tBob ) = 1
then output
(secure, KAKey (rBob , mAlice ))
otherwise output
(normal, KAKey (rBob , mAlice )).
Fig. 2. The Covert-AKA scheme. (KAAlice , KABob , KAKey ) is the passively secure key agreement from Sect. 3.2.
Tag prf is the Message Authentication Code from Sect. 3.1.
the Universal Composability (UC) paradigm of Canetti [10]. There is no space here for a general
introduction to the UC framework. Let us just highlight that in the UC framework a protocol Π is
defined secure with respect to an ideal functionality F which it is supposed to “emulate”. The security
definition guarantees that if another protocol uses Π as a subroutine one can simply replace each call
to Π with a call to F . This holds if the protocols are executed in an arbitrary way, and even if several
instances of the same protocol are executed concurrently. To achieve this strong property the security
definition has to take into account that the inputs of the honest parties can be chosen in an arbitrary
way. This is modeled by introducing a machine called environment Z that is responsible for choosing
the inputs.
The ideal functionality of the UC PAK is presented on Fig. 4 in the appendix. Informally, the main
security guarantees of the UC PAK are as follows. Suppose that the parties are Alice and Bob, each of
them holding a password πAlice , and πBob , resp. At the end of the execution both parties obtain either
1. the same uniformly-random session key sk — if πAlice = πBob and the adversary did not attempt
to compromise the session,
2. two different uniformly-random keys sk Alice and sk Bob (resp.), chosen independently — if πAlice 6=
πBob or the adversary attempted to compromise the session,
The adversary can compromise the session either by guessing a password (he has a right to one such
guess), or by corrupting one of the parties. In both cases he has a right to choose the keys that the
parties receive. Unless the adversary compromised the session, the only information that he obtains
is the fact the the parties executed the protocol. He does not even learn what was the output of the
protocol, i.e. if the parties agreed on the same key sk (Case 1 above) or if each of them received a
different key chosen independently (Case 2). We will use this property in our construction.5
An important feature of the UC framework is that the inputs of the users (in this case: πAlice and
πBob ) are chosen by the environment Z and hence, for example, it may be the case that πAlice and πBob ,
although not equal, are in some way correlated. In reality some correlation like this is not an unusual
case, since it happens, for example, if a user mistypes his password. Another usefull feature of the UC
PAK is that it provides the forward-security, in other words, guessing the password after the session
was completed does not give the adversary any additional information.
The first UC PAK was constructed in [11], and proven secure in the common reference string
model under the standard number-theoretic assumptions. In [1] the authors prove (in the random
oracle model) that one of the existing, more efficient protocols [8] is also UC-secure.
3.5
Private Equality Test
We will also use a tool called a Private Equality Test (PET) (also known as “Socialist Millionaires
Protocol”), which is a scheme executed between two parties, Alice and Bob, holding some inputs xAlice ,
and xBob , resp. The output of Bob is just one bit, namely the information whether xAlice = xBob , and
Alice learns nothing from the protocol. Such protocol can be constructed using generic methods for
the secure two-party computations (see, e.g. [13]). Also, concrete, efficient PET protocols exist (see
e.g. [25]).
4
The construction
4.1
Modeling captcha
It is non-trivial to model Captcha in a proper way. We define a captcha scheme to be a pair (G, H),
where G is a randomized algorithm called a captcha generator that takes as input a string x ∈ {0, 1}∗
and outputs a captcha G(x), and H is a solution function such that we always have H(G(x)) = x. We
say that (G, H) is secure if for every poly-time adversary A and for x chosen uniformly at random
from {0, 1}m we have that
|P (A(G(x)) = x)| is negligible in m.
(2)
Our model is inspired by [12], the main difference being that we explicitly assume that for any solution x
one can efficiently generate the Captcha puzzles that have x as their solution (by calculating y := G(x)).
This makes the description of our protocol a bit simpler, and it also excludes the Captchas where the
creator of the puzzle does not know the entire solution to it (an example of such a system is the
reCaptcha scheme described in Sect. 1.1). In fact, our protocol works only with the Captchas were the
complete solution is known to its creator. Observe that we do not assume anything about the nonmalleability of the Captcha puzzles, i.e. it may be possible for the adversary that knows some puzzle
z = G(x) to produce (without decoding x) a puzzle that z 0 such that H(z 0 ) is in some way related
to x. This corresponds to the real-life situation, where the Captcha puzzles are indeed malleable (for
example, removing the first letter from a graphical representation of a text may be easy, even if the
whole text is unreadable — consider e.g. the image on Fig. 1). Observe also, that the only thing that
5
In [11] the authors say that they are not aware of any application where this is needed. In fact, it may the
first application when this feature is used.
we require in (2) is that the whole solution x is hard to compute, and a Captcha scheme may satisfy
our definition even if some part of x is not hidden from the adversary.
To make our model more realistic, we could relax this definition a little bit and require that the
probability in (2) is smaller than some p(m) (where p is a function that would be a parameter in the
definition, and could be non-negligible). We do not do it since it would complicate our exposition.
A subtle point is how to model the human adversary. As explained in Sect. 2 the adversary can
always break the security of some sessions if he uses a human to solve the Captchas, and an important
property of our scheme is that only those sessions get broken. Therefore, we need somehow to capture
the fact that an adversary “used a human” in some session. To do it, we introduce a captcha oracle
ΩG,H , which is a machine that accepts requests
– captcha(x) – in this case the oracle replies with G(x),
– solve(y) — in this case the oracle replies with H(y).
In this way we will be able to attach a formal meaning to the expression: “the adversary broke a
Captcha of a user Pi ”: we will say it if the user sent a solve(y) request to the oracle, where y was
an output of G(x) and x was captcha(x) was sent to the oracle by Pi . Since we did not assume that
Captchas are non-malleable, the adversary could of course “cheat” and send a solve request with a
slightly modified y, to circumvent this definition. In order to prevent it, we require that the adversary
is only allowed to send solve(y) queries for those y’s that in the past were produced as output by the
oracle in a response to a captcha(x) query. This restriction may look quite arbitrary, but it is hard to
think about any alternative. Observe that, since the Captchas are malleable, in principle there can exist
a way to combine several Captchas y1 = captcha(x1 ), . . . , yt = captcha(xt ) into one “super-Captcha”
whose solution would solve all y1 , . . . , yt . Therefore to reason formally about it, we would somehow
need to be able to measure the “amount of human work” that the adversary invested into breaking the
protocol. Since the goal of this paper is to present the protocol, not to introduce a new formal model,
we do not investigate it further.
4.2
An informal description of the Human Key Agreement protocol
The high-level description of the model was already presented in Sect. 2. Before defining it formally we
give an informal description of the protocol. Recall that the key point of the protocol is the Simultaneous
Turing Test, which is a procedure that allows two parties to test if they are both human, in such a
way that if one of them is not human he will not learn weather the other is human or not. Before
defining the model formally, we provide an informal description of the protocol. Consider two players,
Alice and Bob, holding inputs humanAlice and humanBob , resp., where for P ∈ {Alice, Bob} we have
humanP = 1 if and only if the player P wants to use the secure mode (and hence is willing to solve
Captchas).
At the beginning Alice and Bob select randomly two strings xAlice and xBob , resp. Then each of
them creates a Captcha whose solution is the string that he has chosen, i.e. Alice calculates yAlice :=
captcha(xAlice ) and Bob calculates yBob := captcha(xBob ). Afterwards, they send to each other, over
an insecure link, the values yAlice and yBob , together with their identities (Alice and Bob), and a bit
indicating their roles in the protocol (Alice sends 0 and Bob sends 1). Now, Alice does the following:
if humanAlice = 1 then she solves the Captcha yBob , and sets x0Bob := solve(yBob ), and otherwise she
sets x0Bob to be equal to some default value ((0, . . . , 0), say). Bob does a symmetric thing, i.e. he solves
yAlice if and only if humanBob := 1, setting x0Alice := solve(yB ) and setting x0Alice := (0, . . . , 0). Denote
πAlice = (xAlice , x0Bob ) and πBob = (x0Alice , xBob ).
Now, observe that if the adversary did not disturb the communication then we have that
πAlice = πBob
if and only if
humanAlice = humanBob = 1.
If this is the case then we will denote the value of humanAlice (= humanBob ) with πAlice,Bob . If the
adversary did disturb the communication then he can always cause (xAlice , x0Bob ) 6= (x0Alice , xBob ), just
by modifying one of the Captchas that were sent over the insecure network, but as long as he is
not a human it is infeasible for him to cause (xAlice , x0Bob ) = (x0Alice , xBob ), if humanAlice 6= 1, or
humanBob 6= 1, since to do this he would need to solve a Captcha himself.
Observe also that a machine-adversary has negligible chances of deciphering xAlice and xBob , and
hence, if humanAlice = humanBob = 1 then the value of πAlice,Bob is hidden from him. Moreover,
observe that until this point the players did not send to each other the Captcha solutions, and hence
the values of humanP remain secret.
In the second phase, the players execute a UC PAK with Alice setting her password to (Alice, Bob, πAlice ),
and Bob setting his password to (Alice, Bob, πBob ). From the properties of UC PAK if πAlice = πBob and
the execution of the protocol was not disturbed actively by the adversary, then the parties will agree on
a common key sk . If πAlice 6= πBob then the parties will receive two independent and uniformly-chosen
keys sk and sk 0 . The adversary can cause the same effect by actively disturbing the communication
during the execution of PAK. The important thing is, however, that he does not get any information
about the inputs πAlice and πBob , which in turn implies that, no matter what his actions are, he does
not know the inputs humanAlice and humanBob . Hence, after the second phase the players either share
the same key sk , or have to independent keys sk Alice and sk Bob , resp. Now:
– If sk Alice 6= sk Bob (which happened either because humanAlice ∧ humanBob = 0, or because the
adversary disturbed the communication), then the users will generate a new fresh key for communication. Of course this key will be secure only against a passive adversary (since the users do not
share any secret)
– If the users share the same key (i.e. sk Alice = sk Bob ) then they can use this key to establish a
common session key, using an authenticated key agreement.
Of, course the adversary should not be able to distinguish which was the case (since it would give
him information about humanAlice ∧ humanBob ). Here we use the Covert-AKA (see Sect. 3.3), that is
constructed exactly for this purpose: it allows Alice and Bob, that have keys keys sk A and skB , resp. to
establish a common key. If sk A = sk B then it is a normal AKA, if sk A and sk B are independent, then
it is a passively secure key agreement. The users are notified which was the case, while the adversary
does not know it. The Human Key Agreement protocol is depicted on Fig. 3.
4.3
A formal model
In this section we present a formal definition of our model. An important point is that we have to
take into account that several players may execute the protocol concurrently. Since in our model the
adversary fully controls the network, we cannot prevent him from hijacking a message that some player
Pi to sent to Pj , and forwarding it to some other Pk . Therefore, the players, during the execution of
the protocol have to exchange their identities. Of course, if Pk is malicious then he can falsely claim
to be Pi (we cannot prevent it). So, from the point of view of Pi the security guarantee is as follows:
he knows that either he is talking to Pj , or he is talking to some malicious human (since an honest
Alice
Bob
Phase 1
selects a random xAlice
computes yAlice := captcha(xAlice )
selects a random xAlice
computes yBob := captcha(xBob )
(Alice,yAlice ,0)
−−−−−−−−−→
(Bob,yBob ,1)
←−−−−−−−
if humanAlice = 1 then
set x0Bob := solve(yBob )
otherwise
set x0Bob := (0, . . . , 0).
if humanBob = 1 then
set x0Alice := solve(yAlice )
otherwise
set x0Alice := (0, . . . , 0).
set πAlice := (Alice, Bob, xAlice , x0Bob )
set πBob := (Alice, Bob, x0Alice , xBob )
π
π
Alice
−−−
−→
Phase 2
Bob
←−
−−
UC PAK
sk Alice
Bob
−−−→
sk
sk
←−Bob
−−
←−−−−
sk
Alice
−−−
−→
Phase 3
Covert
AKA
out
←−−Alice
−−−
Output (Bob, 0, out Alice )
out
Bob
−−−−→
Output (Alice, 1, out Bob )
Fig. 3. The Human Key Agreement Protocol. Each out P is equal to (secure, K), (normal, K) or error . The
reason why Alice outputs (Bob, 0, out Alice ) instead of just outputting out Alice is required by the formal model
(that we define in Sect. 4.3) to make sure that the parties have a consistent view on who started the protocol,
and what is the identity of the other party.
Pk would reveal to him that his identity is Pk , not Pj ). Hence, in our model there is no difference
between a malicious participant, and a human-adversary. Therefore, for simplicity, we assume that all
the players are honest.
Other simplifying assumption that we make is that we will consider only two variants of the
adversary: passive or active — in principle the adversary could passively attack some pairs of users,
and actively attack the others, but modeling if formally would just complicate the presentation.
We also assume that the each user Pi decides at the beginning of the protocol if he wants to connect
securely to all the other users (by setting his flag humani := 1). We in fact assume that humani = 1
with probability 1/2. This choice is made just not to make the mode too complicated. In fact, our
protocol is secure also secure if the users can decide adaptively during the execution of the protocol
that to which users they want to connect securely, and to which not.
The adversary in our model is very powerful: he fully controls the network, and he can initiate
the sessions between the players by sending request start(Pi , Pj , r ole) (where r ole is a bit indicating
which party initiates the protocol). For simplicity, we assume that each pair of users generates the key
at most one with the same roles (hence, at most twice in total).
Formally, a Human Key Agreement protocol is a set of players P = {P1 , . . . , Pn } represented as
interactive randomized machines. An adversary is a randomized poly-time interactive machine. The
adversary may be passive or active. Let 1m be a security parameter that all the players and the
adversary take as input. At the beginning each player Pi selects a random bit humani ∈ {0, 1}. Each
player Pi is allowed to send to the oracle ΩG,H the captcha queries. If humani = 1 then Pi is also
allowed to send to the oracle the solve queries. The adversary can send to the oracle captcha and solve
queries, with the restriction that he can only send a query solve(y), if some player Pi received y as a
response to his captcha query. In this case we say that the adversary solved a captcha of Pi .
The players start executing the protocol. The execution is divided into rounds. At the beginning
of the execution the players are idle. During the execution the players just wait for the requests from
the adversary. The adversary can wake up each Pi by sending to it a requests start(Pi , Pj , r ole), where
Pj ∈ P and r ole ∈ {0, 1}. We assume that A never sends twice the same message start(Pi , Pj , r ole).
If the adversary is passive then whenever he sends a request start(Pi , Pj , 0) to some Pi in the same
round he also sends start(Pj , Pi , 1) to some Pj . After Pi receives a start(Pi , Pj , r ole) request it wakes
up and starts interacting with Pj (we say that Pi starts a session with Pj ), for a number of rounds.
At the beginning of each round Pi can issue a pair (Pj , m) and m ∈ {0, 1}∗ . These values are passed
to the adversary. If the adversary is passive then he has to deliver m to Pj , i.e. he has to send a pair
(m, Pi ) to Pj . If the adversary is active he can also prevent m from reaching Pj , modify it, send it to
someone else, or fabricate new messages. At the end of the interaction Pi outputs one of the following
values (suppose Pi was woken up by a start(Pi , Pj , r ole) message):
– (Pj , r ole, (secure, Ki,j )), where key Ki,j ∈ {0, 1}m ,
– (Pj , r ole, (normal, Ki,j )), where key Ki,j ∈ {0, 1}m ,
– a message (Pj , r ole, error ).
After producing the output Pi enters again the idle mode (we say that Pi ended the session), and waits
for the next start message from the adversary. At some point the adversary sends to every player Pi a
message end which causes the players to terminate, and a post-execution game starts. During this game
the adversary can start interacting with an oracle ΩG,H . In particular, he can issue solve requests to
the oracle. For every Pi the adversary outputs humanA
i . We say that the protocol humanity-hiding
if for every Pi such that the adversary did not solve Pi ’s captcha before the protocol terminated, the
probability that humanA
i = humani is at most 1/2 + (m), where m is negligible.
For each Ki,j that was output by some of the players during the execution of the protocol a random
bit b ∈ {0, 1} is selected, and the following is calculated and sent to the adversary:
Ki,j
if b = 0
0
K =
uniformly random K ∈ {0, 1}m otherwise.
The adversary outputs bA ∈ {0, 1}. We say that he distinguished Ki,j from random if b = bA . We say
that the Ki,j -session key is secret if the probability (taken over the randomness of the adversary and
the players) that the adversary distinguishes the Ki,j from random is at most 1/2 + (m), where is
negligible. We say that (π, ΩG,H ) is secure if both following conditions holds
– if the adversary is passive then at the end of a session between Pi and Pj player Pi outputs
(Pj , 0, (secure, Ki,j )), and player Pj outputs (Pi , 1, (secure, Ki,j )). Moreover, the key Ki,j is secret.
– if the adversary is active then whenever some Pi outputs (Pj , r ole, (secure, Ki,j )), and the adversary did not solve Pi ’s captcha during the session that led to producing this output, then:
• with overwhelming probability in the same round Pj outputs (Pi , r ole, (secure, Ki,j )), or
(Pi , r ole, error ), and
• the key Ki,j is secret.
Moreover, the protocol has to be humanity-hiding.
4.4
The implementation
The implementation was already discussed informally in Sect. 4.2, and depicted on Fig. 3). We now
present our protocol in the framework from Sect. 4.3. To make our description consistent with the
description in Sect. 4.2 we call the two parties Alice and Bob, instead of Pj and Pj .
The Human Key Agreement protocol
1. Alice receives start(Alice, Bob, 0) message, and Bob receives start(Bob, Alice, 1) message,
2. Alice generates a random xAlice ∈ {0, 1}m and asks the oracle to compute yAlice = captcha(xAlice ).
She sends (Alice, yAlice , 0) to Bob.
3. Bob generates a random xBob ∈ {0, 1}m and asks the oracle to compute yBob = captcha(xBob ). He
sends (Bob, yBob , 1) to Alice.
4. If humanAlice = 1 then after receiving this message Alice asks the oracle to compute x0Bob =
solve(xBob ) (in this case x0Bob = xBob )). Otherwise Alice sets x0Bob := 0m .
She sets πAlice = (Alice, Bob, xAlice , x0Bob ).
5. If humanBob = 1 then after receiving this message Bob asks the oracle to compute x0Alice =
solve(xAlice ) (in this case x0Alice = xAlice )). Otherwise Bob sets x0Alice := 0m .
He sets πBob = (Alice, Bob, x0Alice , xBob ).
6. Alice and Bob execute the UC PAK protocol setting their passwords to πAlice and πBob , resp.
7. Alice and Bob execute the Covert-AKA protocol, let out Alice and out Bob be their respective outputs.
Then, Alice outputs (Bob, 0, out Alice ) and Bob outputs (Alice, 1, out Bob ).
We now have the following:
Lemma 1. The Human Key Agreement protocol constructed above is secure.
Proof (Proof (sketch)). The security of this scheme as a stand-alone protocol was already informally
argued in Sect. 4.2. Now we just argue informally why the protocol is secure in the framework from
Sect. 4.3, i.e. when executed in a large group of players, possibly concurrently with other executions.
First, if the adversary concurrently initiated several sessions of this protocol with Alice and Bob in
the same roles, then the players themselves will detect it, since by the rules of or model, each pair can
execute the protocol at most once (with the same roles).
If the adversary starts several instances of the protocol, with different players, then he can either
– faithfully make the users execute UC PAK with the same passwords (πAlice = πBob ), in which case
they end up with a common key that is unknown to him, or
– he can try to, e.g., start many parallel sessions and forward the messages between them, however,
if even if he forwards the messages between the sessions, the players will detect it during the
execution of PAK.
Moreover, it is easy to see that injecting the messages from other sessions in the Covert-AKE protocol
does not help the adversary (since the tags in the sessions are computed with independent keys).
4.5
Extensions
Multiple tries One of the common problems with Captcha is that even the human users often fail
to solve them correctly. In the protocol presented above, unfortunately, the user cannot distinguish
between the case when the other user made a mistake solving Captcha, or the case when he is talking
to a malicious machine.
We now show how to extend our protocol in such a way that it permits the user to attempt to solve
the Captchas t times (each time he will be challenged with a different Captcha). Our protocol uses
the Private Equality Test (see Sect. 3.5) in the following way. In Step 2 of the Human Key Agreement
protocol from Sect. 4.4 Alice prepares t Captchas yAlice,1 , . . . , yAlice,t . In Step 3 (if humanBob = 1) the
players execute a following procedure PET Bob
for ` = 1, . . . , t:
`
1. Bob attempts to solve yAlice,` , let x0Alice,` be his solution,
2. the players execute the PET protocol with Bob’s input equal to x0Alice,` and Alice’s input equal to
xAlice` . Recall that as a result of PET Bob learns if x0Alice,` = xAlice` , and Alice learns nothing.
If indeed x0Alice,` = xAlice` then Bob knows that he correctly solved yAlice,` . Let `Bob denote the
current value of `. In this moment Bob may stop participating actively in the remaining procedures
Bob
PET Bob
`Bob +1 , . . . , PET t . However, since we want to hide the fact that humanBob = 1, the protocol
need to be performed (with
cannot stop now and the remaining t − `Bob − 1 executions of PET Bob
i
x0Alice,` being set to some default value).
Alice and Bob also execute the same protocol with the roles of the parties swaped. Let nAlice be the
value of n such that Alice can solve the Captcha xBob,` . Of course, the players cannot just communicate
to each other their respective values nAlice and `Bob , since they would reveal to each other they their
values of humanAlice and humanBob .6 Therefore the players execute t2 times the last two steps of the
2
protocol. More precisely, for each pair (`, n) ∈ {1, . . . , t} they execute the Steps 6 and 7 with
6
This is because if, e.g., Alice sends to Bob a message “I solved your `th Captcha” she would automatically
reveal that humanAlice = 1. One could think about the following solution: if humanAlice = 0 then she sends
to Bob a “false” information “I solved your `R th Captcha”, where `R is chosen randomly from {1, . . . , t}.
Unfortunately, it does not work since a malicious machine could prepare the Captchas that are extremely
simple to solve, and hence if `R 6= 1 it would strongly indicate that humanAlice = 0.
– Bob setting xBob := xBob,n , and
x0Alice :=
x0Alice,`Bob if ` = `Bob
(0, . . . , 0) otherwise
– Alice setting xAlice := xAlice,` , and
x0Bob
:=
x0Bob,nAlice if n = nAlice
(0, . . . , 0) otherwise
As a result, if they are both human, and they both succeeded in solving at least one Captcha, then in
one of those t2 steps (namely in (nAlice , `Bob )) they will successfully establish a common key. If one of
them is not a human then all the t2 steps will fail. Therefore a machine-adversary will not learn if one
of the parties is human or not. Note that performing t2 steps described above may be computationally
costly, it is however efficient from the point of view of human time spent on executing it.7 We believe
actually, that the computational complexity of this protocol can be improved, using some methods
from the secure two-party computations literature. We leave it as a future work.
Human-generated puzzles Recall that Captcha stands for “Completely Automated Public Turing
test to tell Computers and Humans Apart”, and hence normally it is assumed that the puzzles are
generated automatically. We note that actually in our case the Captcha puzzles can be generated with
some human assistance (since the creator of Captcha is also a human). This opens a potential to create
Captchas in non-automatic way, hence making them more resilient to the solvers based on artificial
intelligence.
Pornography attacks As described in the introduction, in the pornography attack the attacker
forwards a Captcha to a pornographic web-site, and the web-site users have to solve the Captcha
before being allowed to view the web-site contents [38]. We note that our scheme is vulnerable to this
kind of an attack (one has to hope that in practice it would not be economical to perform such an
attack). An interesting feature of our protocol is that itself it cannot be used for a similar attack,
in other words, the properties of our construction imply that the users cannot be used as oracle for
solving Captchas (this is because the user never sends his Captcha solution to the other users).
5
Conclusions
We believe that the paradigm, especially the Simultaneous Turing Test presented in this paper my be
useful also in other applications. We leave finding these applications as an open research problem.
References
1. Michel Abdalla, Dario Catalano, C´eline Chevalier, and David Pointcheval. Efficient two-party passwordbased key exchange protocols in the uc framework. In Tal Malkin, editor, CT-RSA, volume 4964 of Lecture
Notes in Computer Science, pages 335–351. Springer, 2008.
7
We could actually get rid of the PET protocol and just execute the second step of the procedure. This
however, would force the user to type-in Captcha solutions several times, even if he already solved some of
them correctly (since the user would not have a method of verifying if his solution was correct).
2. Ross Anderson. Two remarks on public key cryptology. Technical report, University of Cambridge,
Computer Laboratory, 2002. Technical report.
3. Dirk Balfanz, Diana K. Smetters, Paul Stewart, and H. Chi Wong. Talking to strangers: Authentication
in ad-hoc wireless networks. In NDSS. The Internet Society, 2002.
4. Mihir Bellare, David Pointcheval, and Phillip Rogaway. Authenticated key exchange secure against dictionary attacks. In EUROCRYPT, pages 139–155, 2000.
5. Steven M. Bellovin and Michael Merritt. Encrypted key exchange: Password-based protocols secure against
dictionary attacks. In Proc. IEEE Computer Society Symposium on Research in Security and Privacy, pages
72–84, Oakland, CA, May 1992.
6. Colin A. Boyd and Anish Mathuria. Protocols for Key Establishment and Authentication. Springer-Verlag
New York, Inc., Secaucus, NJ, USA, 2003.
7. Victor Boyko, Philip D. MacKenzie, and Sarvar Patel. Provably secure password-authenticated key exchange using diffie-hellman. In EUROCRYPT, pages 156–171, 2000.
8. Emmanuel Bresson, Olivier Chevassut, and David Pointcheval. Security proofs for an efficient passwordbased key exchange. In Sushil Jajodia, Vijayalakshmi Atluri, and Trent Jaeger, editors, ACM Conference
on Computer and Communications Security, pages 241–250. ACM, 2003.
9. M. Cagalj, S. Capkun, and J. P. Hubaux. Key agreement in peer-to-peer wireless networks. Proceedings
of the IEEE, 94(2):467–478, January 2006.
10. Ran Canetti. Universally composable security: A new paradigm for cryptographic protocols. In FOCS,
pages 136–145, 2001. Extended version avaialble at http://eprint.iacr.org/2000/067.
11. Ran Canetti, Shai Halevi, Jonathan Katz, Yehuda Lindell, and Philip D. MacKenzie. Universally composable password-based key exchange. In Ronald Cramer, editor, EUROCRYPT, volume 3494 of Lecture
Notes in Computer Science, pages 404–421. Springer, 2005.
12. Ran Canetti, Shai Halevi, and Michael Steiner. Mitigating dictionary attacks on password-protected local
storage. In Cynthia Dwork, editor, CRYPTO, volume 4117 of Lecture Notes in Computer Science, pages
160–179. Springer, 2006.
13. Ronald Cramer. Introduction to secure computation. In Ivan Damg˚
ard, editor, Lectures on Data Security,
volume 1561 of Lecture Notes in Computer Science, pages 16–62. Springer, 1998.
14. W. Diffie and M. E. Hellman. New directions in cryptography. IEEE Transactions on Information Theory,
IT-22(6):644–654, November 1976.
15. Whitfield Diffie, Paul C. van Oorschot, and Michael J. Wiener. Authentication and authenticated key
exchanges. Designs, Codes, and Cryptography, 2(2):107–125, June 1992.
16. C. Ellison and B. Schneier. Ten risks of pki: What you’re not being told about public key infrastructure.
Computer Security Journal, 16(1):1–7, 2000.
17. Oded Goldreich and Yehuda Lindell. Session-key generation using human passwords only. J. Cryptology,
19(3):241–340, 2006.
18. Christoph G. G¨
unther. An identity-based key-exchange protocol. In EUROCRYPT, pages 29–37, 1989.
19. Jonathan Katz and Yehuda Lindell. Introduction to Modern Cryptography. Chapman & Hall/CRC Press,
August 2007.
20. Jonathan Katz, Rafail Ostrovsky, and Moti Yung. Forward secrecy in password-only key exchange protocols. In Stelvio Cimato, Clemente Galdi, and Giuseppe Persiano, editors, SCN, volume 2576 of Lecture
Notes in Computer Science, pages 29–44. Springer, 2002.
21. Gregg Keizer. Spammers’ bot cracks microsoft’s captcha. Computerworld, February 2008. http://www.
computerworld.com/s/article/9061558/Spammers_bot_cracks_Microsoft_s_CAPTCHA_.
22. Arun Kumar, Nitesh Saxena, Gene Tsudik, and Ersin Uzun. A comparative study of secure device pairing
methods. To appear in Pervasive and Mobile Computing Journal (PMC), 2009. available at http://www.
ics.uci.edu/~euzun/.
23. Sven Laur and Kaisa Nyberg. Efficient mutual data authentication using manually authenticated strings.
In David Pointcheval, Yi Mu, and Kefei Chen, editors, CANS, volume 4301 of Lecture Notes in Computer
Science, pages 90–107. Springer, 2006.
24. Mark Lillibridge, Martin Abadi, Krishna Bharat, and Andrei Broder. Method for selectively restricting
access to computer systems. US patent US6195698. Filing date: April 13, 1998.
25. Helger Lipmaa. Verifiable homomorphic oblivious transfer and private equality test. In Chi-Sung Laih,
editor, ASIACRYPT, volume 2894 of Lecture Notes in Computer Science, pages 416–433. Springer, 2003.
26. Philip D. MacKenzie, Sarvar Patel, and Ram Swaminathan. Password-authenticated key exchange based
on rsa. In Tatsuaki Okamoto, editor, ASIACRYPT, volume 1976 of Lecture Notes in Computer Science,
pages 599–613. Springer, 2000.
27. Moni Naor. Verification of a human in the loop or identification via the turing test. http://www.wisdom.
weizmann.ac.il/~naor/PAPERS/human.pdf, 1996.
28. Minh-Huyen Nguyen and Salil P. Vadhan. Simpler session-key generation from short random passwords.
J. Cryptology, 21(1):52–96, 2008.
29. Sylvain Pasini and Serge Vaudenay. Sas-based authenticated key agreement. In Moti Yung, Yevgeniy
Dodis, Aggelos Kiayias, and Tal Malkin, editors, Public Key Cryptography, volume 3958 of Lecture Notes
in Computer Science, pages 395–409. Springer, 2006.
30. A. Perrig and D. Song. Hash visualization: A new technique to improve real-world security. In International
Workshop on Cryptographic Techniques and E-Commerce (CrypTEC), 1999.
31. Reuters Press Release. D-link first to add captcha to its home routers to help prevent against attacks.
http://www.reuters.com/article/pressRelease/idUS118678+12-May-2009+MW20090512, 2009.
32. Claudio Soriente, Gene Tsudik, and Ersin Uzun. Secure pairing of interface constrained devices. Int. J.
Secur. Netw., 4(1/2):17–26, 2009.
33. Frank Stajano and Ross J. Anderson. The resurrecting duckling: Security issues for ad-hoc wireless networks. In Bruce Christianson, Bruno Crispo, James A. Malcolm, and Michael Roe, editors, Security
Protocols Workshop, volume 1796 of Lecture Notes in Computer Science, pages 172–194. Springer, 1999.
34. Carnegie Mellon University. The official captcha site. http://www.captcha.net/.
35. Serge Vaudenay. Secure communications over insecure channels based on short authenticated strings.
In Victor Shoup, editor, CRYPTO, volume 3621 of Lecture Notes in Computer Science, pages 309–326.
Springer, 2005.
36. Luis von Ahn, Manuel Blum, Nicholas J. Hopper, and John Langford. Captcha: Using hard ai problems for
security. In Eli Biham, editor, EUROCRYPT, volume 2656 of Lecture Notes in Computer Science, pages
294–311. Springer, 2003.
37. Luis von Ahn, Benjamin Maurer, Colin Mcmillen, David Abraham, and Manuel Blum. recaptcha: Humanbased character recognition via web security measures. Science, pages 1465–1468, August 2008.
38. BBC News website. Pc stripper helps spam to spread. http://news.bbc.co.uk/2/hi/technology/
7067962.stm, accessed on November 21, 2009, October 2007.
39. BBC News website. China “spying on skype messages”. http://news.bbc.co.uk/2/hi/technology/
7649761.stm, accessed on November 21, 2009, October 2008.
40. Wikipedia. Captcha. http://en.wikipedia.org/wiki/CAPTCHA. Accessed on November 21, 2009.
41. Philip Zimmermann, Alan Johnston, and Jon Callas. Zrtp: Media path key agreement for secure rtp.
Internet draft available at http://zfoneproject.com/docs/ietf/draft-zimmermann-avt-zrtp-16.html.
42. Dimitris Zisiadis, Spyros Kopsidas, and Leandros Tassiulas. Vipsec defined. Comput. Netw., 52(13):2518–
2528, 2008.
Functionality FpwKE The functionality FpwKE is parameterized by a security parameter k. It interacts with
an adversary S and a set of parties via the following queries:
Upon receiving a query (NewSession, sid , Pi , P j, pw , r ole) from party Pi :
Send (NewSession; sid , Pi , Pj , role) to S. In addition, if this is the first NewSession query, or if this is
the second NewSession query and there is a record (Pj , Pi , pw 0 ), then record (Pi , Pj , pw ) and mark
this record fresh.
Upon receiving a query (TestPwd, sid , Pi , pw 0 ) from the adversary S
If there is a record of the form (Pi , Pj , pw ) which is fresh, then do: If pw = pw 0 , mark the record
compromised and reply to S with “correct guess”. If pw 6= pw 0 , mark the record interrupted and reply
with “wrong guess”.
Upon receiving a query (NewKey, sid , Pi , sk ) from S, where |sk | = k:
If there is a record of the form (Pi , Pj , pw ), and this is the first NewKey query for Pi , then:
– If this record is compromised, or either Pi or Pj is corrupted, then output (sid , sk ) to player Pi .
– If this record is fresh, and there is a record (Pj , Pi , pw 0 ) with pw 0 = pw , and a key sk 0 was sent
to Pj , and (Pj , Pi , pw ) was fresh at the time, then output (sid , sk0 ) to Pi .
– In any other case, pick a new random key sk0 of length k and send (sid , sk0 ) to Pi .
Either way, mark the record (P i, P j, pw ) as completed.
Fig. 4. The password-based key-exchange functionality FpwKE of [11]. The role of the sid variable is to distinguish between difference sessions. The role of the r ole variable is to give the users the possibility to check who
initiated the protocol. For more on this see [11].