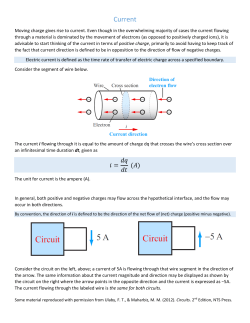
Chapter 18 Electric Currents Electric Current: Flow of electric charge Current is flow of charge per unit time: ∆𝑄 𝐼= . ∆𝑡 Unit of current: Ampere (A). The purpose of a battery is to produce a constant potential difference, which can then make charges move. Current can flow in a circuit only if there is a continuous conducting path. We then have a complete or ‘closed’ circuit. A circuit where there is a break, like, a cut wire, is called an ‘Open’ circuit. The figure shows conventional current, i.e. the flow of positive charge. In reality it’s the electron moves in solids- Electron current. Ohm’s Law : Resistance and Resistors - Current through a wire is directly proportional to applied voltage. 𝐼∝𝑉 Removing the sign of proportionality, 𝑉 = 𝐼𝑅 where ‘𝑅’ is called the ‘Resistance’ of the circuit. It has been also seen that the Resistance of a wire is directly proportional to the length of the wire and inversely proportional to the cross sectional area of the wire. Mathematically, 𝑙 𝑅=𝜌 𝑎 Where 𝜌 is called the ‘Resistivity’ of the wire. The Resistivity depends only the temp of the surrounding. Temperature Dependence of Resistivity: 𝜌𝑇 = 𝜌0 1 + 𝛼 𝑇 − 𝑇0 𝜌0 : Resistivity at some reference Temperature 𝑇0 𝜌𝑇 : Resistivity at temperature T 𝛼: Temperature coefficient of resistivity Electric Power: 𝐸𝑛𝑒𝑟𝑔𝑦 𝑇𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑒𝑑 𝑄𝑉 𝑃= = = 𝐼𝑉 𝑡𝑖𝑚𝑒 𝑡 Also, 𝑉 = 𝐼𝑅. So, 2 𝑉 𝑃 = 𝐼𝑉 = 𝐼 2 𝑅 = 𝑅 Unit of Power(P): Watt (W). 1W = 1 J/s. Household Circuits: - Connected such that each appliance gets same Voltage (Parallel connection). - When a wire carries more that its safe, the circuit is called overloaded, which causes heating, and fire. To prevent this we use circuit breaker or fuses. - Each wire has a limit up to which it can hold current (Current Rating), after which the heat produced at the rate of I2R is too high for the insulating material. Problem 1: A hair dryer draws 13.5 A when plugged into a 120V line. a) What is the resistance ? b) How much charge passes through it in 15 min. (Assume direct current ). Solution: a) Ohm’s Law: V=IR. So, R = V/I = 120/13.5 = 8.88 Ω b) Current, I = charge/time = Q/t So, Charge (Q) =I x t =13.5 X 15 x 60s = 12150C. Problem 2: Two aluminum wires have the same resistance. If one has twice the length of the other, what is the ratio of the diameter of the longer wire to the shorter wire? Solution: 𝑙𝑙 For longer wire: 𝑅𝑙 = 𝜌 For shorter wire: 𝑅𝑠 = 𝑎𝑙 𝑙𝑠 𝜌 𝑎𝑠 According to the problem, Rl = Rs 𝑙𝑙 𝑙 So, = 𝑠 𝑎𝑙 𝑎𝑙 𝑎𝑠 = 𝑙𝑙 𝑙𝑠 =2 𝑎𝑠 or, 𝑑𝑙 𝑑𝑠 = 2 Problem 3: At $0.095/kWh, what does it cost to leave a 25W porch light on day and night for a year ? Solution: kWh (kilo-Watt hour)is the unit of energy. This is the unit that your electric company use to charge for your electricity consumption. If 1000W power is used in 1 hour, we say the appliance consumed 1kWh of energy. Thus, Total energy Spent by the porch light = 25 W x 1 year = 25 W x 365 x 24 hours = 219000 Watt- hour = 219kWh. So, total cost = 219 x$0.095 = $20.8 Problem 4: A 100 W light bulb has a resistance of about 12 ohm when cold (200C ) and 140 Ohm when on (hot). Estimate the temperature of the filament when hot assuming the temperature coefficient of resistivity α = 0.0045(C0)-1. Solution: 𝑙 𝜌𝑇 = 𝜌0 1 + 𝛼 𝑇 − 𝑇0 Remember: 𝑅 = 𝜌 𝑎 Hence for constant ‘𝑙’ and ‘a’, we can replace 𝜌 by R. Thus, 140 = 12 [1+ 0.0045(T-20)] So, T = 2390 0C. Alternating Current (AC): - Reverses direction many times a second, and are usually sinusoidal. All currents supplied to household are AC all over the world. The voltage produced by generators are sinusoidal and can be expressed as a function of time as: 𝑉 = 𝑉0 𝑠𝑖𝑛2𝜋𝑓𝑡 = 𝑉0 𝑠𝑖𝑛𝜔𝑡 Ohm’s law also holds good for ac. Hence, above equation can be written as: 𝐼 = 𝐼0 𝑠𝑖𝑛𝜔𝑡 𝐼0 𝑎𝑛𝑑 𝑉0 : Peak Current and Peak Voltage. Over a full cycle, the average current is zero. This would imply the power is also zero, but this is not the case. The electron is losing some energy at every instant whether it be moving forward or backward in a circuit. At a given time t, the power transformed in the resistance R is: 𝑃 = 𝐼 2 𝑅 = 𝐼02 𝑅𝑠𝑖𝑛2 𝜔𝑡 You can also see from this equation, 𝐼02 is always positive. Also, the value of sine lies between -1 and 1. But as it is squared, it is also positive. Average of 𝑠𝑖𝑛2 𝜔𝑡 = 1/2. (Refer to your textbook.) Hence the average power transformed is , 1 2 1 𝑉02 𝑃 = 𝐼0 𝑅 = 2 2 𝑅 Since using the average current or voltage values for ac will predict zero power transformed over a cycle, which is not true, we take the square of the average of these quantities. This is called the root mean square (rms) value of current or voltage: 𝐼0 2 𝐼𝑟𝑚𝑠 = 𝐼 = = 0.707𝐼0 2 𝑉0 2 𝑉𝑟𝑚𝑠 = 𝑉 = = 0.707𝑉0 2 So, the average power can also be calculated as, 1 2 2 𝑃 = 𝐼𝑟𝑚𝑠 𝑉𝑟𝑚𝑠 = 𝐼0 𝑅 = 𝐼𝑟𝑚𝑠 𝑅 2 2 2 1 𝑉0 𝑉𝑟𝑚𝑠 = = 2 𝑅 𝑅 This implies that in order to generate same power, the I and V used is direct current (dc) is replaced by its rms values of I and V in ac. In USA, the standard line voltabe is 120V-ac, and is the rms value. Microscopic View of Electric Current When electric current is passed through a wire, the electron attains a steady velocity, which is called the drift velocity (vd). As the electron collide with the atoms of the wire, it cannot accelerate further. Let n be the number of charges per unit volume. Then, ∆Q = Number of charges x Charge per particle = (nV)e = (nAvd Δt)(e) So, magnitude of Current I in the wire: I = ΔQ/ Δt = neAvd Problem 5: Determine the maximum instantaneous power dissipated by a 2.2hp pump connected to a 240 Vrms ac power source, and the maximum current passing through the pump. Solution: 1hp = 746 Watt Prms= Vrms x Irms Hence, Irms =2.2 x 746/240 V = 6.84 A. R= Vrms/Irms = 240/6.84 = 35.08 Ohms Pmax = V2max/R = 2 X 2402/35.08 = 3291 Watt. Where ‘2’ is because Vmax = 1.414 x Vrms So, Ipeak = 1.414 x Irms = 9.67 A Problem 6: A 0.65mm diameter copper wire carries a tiny dc current of 2.7μA. Estimate the electron drift velocity. Solution: We know I = neAvd. All we need to calculate is ‘n’. Let us determine n for one mole of Copper as it is the standard unit of measurement. Hence, 𝑁 𝑁 𝑁 𝑛= =𝑚 = 𝜌 𝑉 𝜌 𝑚 For one mole, 𝑛 = Hence, 𝑣𝑑 = 𝐼 𝑛𝑒𝐴 𝑁 (1 𝑚𝑜𝑙𝑒) 𝜌 𝑚(1 𝑚𝑜𝑙𝑒) = 6.023×1023 = × 8.9 × 63.5×10−3 𝐾𝑔 = 8.4 × 1028 𝑚−3 2.7 ×10−6 8.4 ×1028 ×1.6×10−19 ×𝜋× 2 0.65×10−3 2 103 𝑘𝑔/𝑚3 = 6 × 10−10 𝑚