1. No category

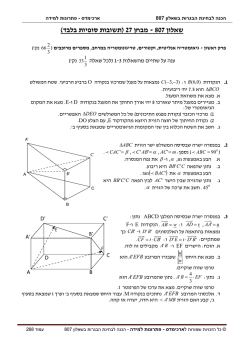
‫מבחן בגרות מספר ‪7‬‬
‫קיץ תשע"א‪ ,2011 ,‬מועד א‬
‫פרק ראשון – אלגברה והסתברות‬
‫ענה על שתיים מבין השאלות ‪. 3-1‬‬
‫‪.1‬‬
‫במפעל לייצור מחשבונים עובדים פועלים ותיקים ופועלים חדשים‪.‬‬
‫פועל ותיק ופועל חדש התבקשו להרכיב מחשבונים‪.‬‬
‫לו פועל ותיק היה עובד ‪ 1‬מהזמן שנדרש לעובד חדש לבצע לבד עבודה זו‪,‬‬
‫‪3‬‬
‫ופועל חדש היה עובד ‪ 1‬מהזמן שנדרש לעובד ותיק לבצע לבד עבודה זו‪,‬‬
‫‪3‬‬
‫אז יחד הם היו מבצעים ‪ 13‬מעבודה זו‪ .‬פועל ותיק מבצע לבד את העבודה‬
‫‪18‬‬
‫במספר שעות קטן יותר מז ה הדרוש לפועל חדש‪.‬‬
‫א‪ .‬מצא פי כמה גדול מספר השעות הדרוש לפועל חדש לבצע לבד‬
‫את העבודה‪ ,‬ממספר השעות הדרוש לפועל ותיק לבצע לבד את העבודה‪.‬‬
‫ב‪ .‬נתון כי פועל ותיק מרכיב ‪ 9‬מחשבונים בשעה‪.‬‬
‫בצוות עבודה יש פועל אחד חדש ושנ י פועלים ותיקים‪.‬‬
‫מצא בכמה שעות הצוות מרכיב ‪ 168‬מחשבונים‪.‬‬
‫‪.2‬‬
‫נתונה סדרה הנדסית אין‪ -‬סופית יורדת‪.‬‬
‫כל איבר בסדרה זו קטן פי ‪ 2‬מסכום כל האיברים שאחריו‪.‬‬
‫סכום הסדרה ההנדסית הנתונה הוא ‪. 4‬‬
‫מצא את סכום כל האיברים שאחרי האיבר העשירי בסדרה‪.‬‬
‫‪.3‬‬
‫בחברת תקשורת גדולה נבדקו הרגלי הצפייה של הלקוחות‪.‬‬
‫נמצא כי מספר הלקוחות שצופים בערוצי אקטואליה גדול פי ‪ 4‬ממספר‬
‫הלקוחות שאינם צופים בהם‪ 5 .‬מהלקוחות שצופים בערוצי סרטים‪,‬‬
‫‪6‬‬
‫צופים בערוצי אקטואליה‪.‬‬
‫‪ 75%‬מהלקוחות שאינם צופים בערוצי סרטים‪ ,‬צופים בערוצי אקטואליה‪.‬‬
‫בוחרים באקראי לקוח מבין הלקוחות שהרגלי הצפייה שלהם נבדקו‪.‬‬
‫ההסתברות שהוא צופה בערוצי סרטים היא ‪. P‬‬
‫א‪ ( 1 ) .‬הבע באמצעות ‪ P‬את ההסתברות שהלקוח שנבחר צופה בערוצי‬
‫סרטים וגם בערוצי אקטואליה‪.‬‬
‫) ‪ ( 2‬מצא את ‪. P‬‬
‫‪26‬‬
‫ב‪ ( 1 ) .‬נמצא שהלקוח שנבחר אינו צופה בערוצי סרטים‪.‬‬
‫מהי ההסתברות שהוא אינו צופה בערוצי אקטואליה?‬
‫) ‪ ( 2‬בחרו באקראי ‪ 5‬לקוחות שאינם צופים בערוצי סרטים‪.‬‬
‫מהי ההסתברות שלפחות אחד מהם צופה בערוצי אקטואליה?‬
‫פרק שני – גאומטריה וטריגונומטריה במישור‬
‫ענה על אחת מבין השאלות ‪. 5-4‬‬
‫‪.4‬‬
‫נתון משולש ‪ . ABC‬הנקודות ‪ , E , D‬ו‪F -‬‬
‫נמצאות על הצלעות ‪ , AC , AB‬ו‪ BC -‬בהתאמה‬
‫כך ש‪ DE  BC -‬ו‪) FE  BA -‬ראה ציור(‪.‬‬
‫א‪ .‬נתון‪ :‬שטח המשולש ‪ ADE‬הוא ‪, S1‬‬
‫‪E‬‬
‫שטח המשולש ‪ EFC‬הוא ‪. S2‬‬
‫‪C‬‬
‫הבע באמצעות ‪ S1‬ו‪S2 -‬‬
‫את היחס ‪BF‬‬
‫‪ .‬נמק‪.‬‬
‫‪FC‬‬
‫ב‪ .‬הוכח כי שטח המשולש ‪ BEF‬שווה ל‪. S1  S2 -‬‬
‫‪.5‬‬
‫לשני מעגלים יש משיק משותף המשיק לשניהם בנקודה ‪. P‬‬
‫‪A‬‬
‫‪D‬‬
‫‪B‬‬
‫‪F‬‬
‫נק ודות ‪ C‬ו‪ D -‬נמצאות על מעגל אחד‬
‫‪C‬‬
‫ונקודות ‪ A‬ו‪ B -‬נמצאות על המעגל‬
‫‪A‬‬
‫האחר כך שהקטעים ‪ AD‬ו‪CB -‬‬
‫נפגשים בנקודה ‪) P‬ראה ציור(‪.‬‬
‫‪P‬‬
‫נתון‪ :‬רדיוס המעגל העובר דרך הנקודות‬
‫‪ D , C‬ו‪ P -‬הוא ‪ 4.5‬ס"מ‪CD  3 ,‬‬
‫‪AB 2‬‬
‫‪. DCP   , BAP  ‬‬
‫‪,‬‬
‫‪D‬‬
‫א‪ .‬מצא את רדיוס המעגל העובר דרך הנקודות ‪ B , A‬ו‪. P -‬‬
‫ב‪ .‬הבע באמצעות ‪ ‬ו‪  -‬את אורך הקטע ‪. BD‬‬
‫ג‪ .‬אם נתון גם כי ‪PD  3‬‬
‫‪PB 2‬‬
‫) ‪ ‬ו‪  -‬הן זוויות חדות‪(.‬‬
‫‪2‬‬
‫‪ ,‬הראה כי ‪. BD  3sin   1  24sin ‬‬
‫‪27‬‬
‫‪B‬‬
‫פרק שלישי – חשבון דיפרנציאלי ואינטגרלי של פולינומים‪,‬‬
‫של פונקציות רציונליות‪ ,‬של פונקציות שורש ושל פונקציות‬
‫טריגונומטריות‬
‫ענה על שתיים מבין השאלות ‪. 8-6‬‬
‫‪.6‬‬
‫נתונה הפונקציה‬
‫‪ax‬‬
‫‪2‬‬
‫‪x  a2‬‬
‫‪ a . f (x) ‬הוא פרמטר שונה מאפס‪.‬‬
‫א‪ .‬עבור ‪ a  0‬מצא )הבע באמצעות ‪ a‬במידת הצורך(‪:‬‬
‫) ‪ ( 1‬את תחום ההגדרה של הפונקציה‪.‬‬
‫) ‪ ( 2‬את האסימפטוטות של הפונקציה המקבילות לצירים‪.‬‬
‫) ‪ ( 3‬תחומי עלייה וירידה של הפונקציה )אם יש כאלה(‪.‬‬
‫) ‪ ( 4‬נקודות חיתוך של גרף הפונקציה עם הצירים )אם יש כאלה(‪.‬‬
‫ב‪ .‬ס רטט סקיצה של גרף הפונקציה עבור ‪. a  0‬‬
‫ג‪ .‬נתונה הפונקציה ‪. a  0 , g(x)  f (x)  a‬‬
‫) ‪ ( 1‬מה הן האסימפטוטות של הפונקציה )‪? g(x‬‬
‫)הבע באמצעות ‪ a‬במידת הצורך(‪.‬‬
‫) ‪ ( 2‬מה הם ה ערכים שהפונקציה )‪ g(x‬יכולה לקבל?‬
‫)הבע באמצעות ‪ a‬במידת הצורך(‪.‬‬
‫‪.7‬‬
‫נתונה הפונקציה )‪ f (x)  cos(x 2  2x‬בתחום ‪. 0.5  x  2.5‬‬
‫א‪ .‬בתחום הנתון מצא את השיעורים של נקודות הקיצון של הפונקציה‪,‬‬
‫וקבע את סוגן‪.‬‬
‫ב‪ .‬בתחום הנתון שרטט סקיצה של גרף הפונקציה‪.‬‬
‫ג‪ .‬בתחום ‪ 0  x  2‬מצא את השטח המוגבל על ידי הגרף של פונקציית‬
‫הנגזרת )‪ f '(x‬ועל ידי ציר ה‪. x -‬‬
‫תוכל להיעזר בסקיצה של פונ קציית הנגזרת )‪. f '(x‬‬
‫בתשובותיך דייק במידת הצורך עד שתי הספרות אחרי הנקודה העשרונית‪.‬‬
‫‪28‬‬
‫‪.8‬‬
‫נתונה מדשאה בצורת מלבן ‪. ABCD‬‬
‫לאורך צלעות המלבן ‪ BA‬ו‪ CD -‬יש שב ילי הליכה‪.‬‬
‫אורך הצלע ‪ BA‬הוא ‪ 0.4‬ק"מ‪,‬‬
‫‪B‬‬
‫‪F‬‬
‫שביל‬
‫‪A‬‬
‫ואורך הצלע ‪ BC‬הוא ‪ 0.3‬ק"מ‪.‬‬
‫אדם עומד בקדקוד ‪ C‬של המדשאה‬
‫ורוצה להגיע לקדקוד ‪ . A‬הוא הולך‬
‫לאורך הקטע ‪ CE‬שעל השביל ‪, CD‬‬
‫אחר כך הולך לאורך הקטע ‪ EF‬שעל המדשאה‬
‫‪C‬‬
‫‪E‬‬
‫שביל‬
‫‪D‬‬
‫וממשיך לאורך הקטע ‪ FA‬שעל השביל ‪) BA‬ראה ציור(‪.‬‬
‫האד ם הולך במהירות של ‪ 6‬קמ"ש לאורך השבילים‪,‬‬
‫ועל המדשאה הוא הולך במהירות של ‪ 4‬קמ"ש‪.‬‬
‫מה צריך להיות אורך הקטע ‪ , EF‬כדי שהאדם יגיע ל‪ A -‬בזמן הקצר‬
‫ביותר? בתשובתך די יק עד שתי ספרות אחרי הנקודה העשרונית‪.‬‬
‫תשובות ל מבחן בגרות מספר ‪ – 7‬קיץ תשע"א‪ , 2011 ,‬מועד א‬
‫‪ . 1‬א‪ .‬פי ‪ . 1.5‬ב‪ 7 .‬שעות‪.‬‬
‫‪. 4096 . 2‬‬
‫‪59049‬‬
‫‪S1‬‬
‫‪ . 3‬א‪ . P  0.6 ( 2 ) . 5 p ( 1 ) .‬ב‪ . 4 . 1023 ( 2 ) . 0.25 ( 1 ) .‬א‪.‬‬
‫‪1024‬‬
‫‪6‬‬
‫‪S2‬‬
‫‪.‬‬
‫‪2‬‬
‫‪2‬‬
‫‪ . 5‬א‪ 3 .‬ס"מ‪ .‬ב‪. BD  36sin   81sin   108sin  sin  cos(  ) .‬‬
‫‪ . 6‬א‪ x  a ( 1 ) .‬או ‪. x   a‬‬
‫) ‪. y  a , y  a , x   a , x  a ( 2‬‬
‫) ‪ ( 3‬עלייה‪ :‬אף ‪ ; x‬ירידה‪ x  a :‬או ‪ ( 4 ) . x   a‬אין חיתוך עם הצירים‪.‬‬
‫‪y‬‬
‫ב‪ .‬עבור ‪: a  0‬‬
‫‪x‬‬
‫ג‪. y  2a , y  0 , x  a , x  a ( 1 ) .‬‬
‫) ‪ g(x)  0 ( 2‬או ‪. g(x)  2a‬‬
‫‪ . 7‬א‪ ( 0.5;0.315) .‬מינימום‪ (0;1) ,‬מקסימום‪ (1;0.54) ,‬מינימום‪ (2;1) ,‬מקסימום‪,‬‬
‫)‪ (2.5;0.315‬מינימום‪.‬‬
‫‪y‬‬
‫ב‪.‬‬
‫ג‪. 0.92 .‬‬
‫‪ 0.4025 . 8‬ק"מ‪.‬‬
‫‪x‬‬
‫‪29‬‬