‫שער לים ‪Sea Gate‬‬ ‫פרק ה ‪ :‬יסודות בפיזיקה ונושאי רקע לפרקים ו ‪ ,‬ז ‪ ,‬ח‬ ‫‪.1‬‬ ‫‪.2‬‬ ‫‪.3‬‬ ‫‪.4‬‬ ‫‪.5‬‬ ‫‪.6‬‬ ‫פרקים אלה מתיחסים לימאות המעשית ‪ ,‬אשר נ י תן ללמוד אותה רק מנסיון‪,‬‬ ‫חשוב יותר מכל לימוד היא ההתנסות במה שמכונה " מיקרים ותגובות "‪.‬‬ ‫הלימוד כאן מתייחס לשיט שמטרתו להביא את השטים מנקודה אחת לנקודה שניה ‪,‬‬ ‫ביעילות המירבית שנתן להפיק מכלי שיט נתון ‪ .‬השיט התחרותי חופף לחלק‬ ‫מההתיחסות ‪ ,‬אך מנוגד וסותר את הגישה של " ימאות טובה " ‪ ,‬אין כאן כיסוי של‬ ‫חלק זה של השיט‪ ,‬אלא אם ‪ ,‬באופן מקרי‪ ,‬יש חפיפה בדרישות ‪.‬‬ ‫אל תטרח לקרא אם באפשרו תך לשוט‪ ,‬חזור וקרא אחרי השיט או כשתגיע לגיל שבו‬ ‫קוראים וכותבים במקום לשוט ‪...‬‬ ‫כל פעולה‪ ,‬שנלמדת או מלומדת ראוי שמייד ‪ ,‬בצמוד אליה‪ ,‬תלמד הפעולה להפסקת‬ ‫התהליך והפעולה ההפוכה ‪ .‬לדוגמה מייד עם לימוד התנעת מנוע יש ללמוד כיבוי‬ ‫מנוע ‪ ,‬מייד עם הורדת עוגן יש ללמוד הרמת עוגן‪ ,‬מייד עם הרמת מפרש יש ללמוד‬ ‫צמצום והורדה וכך הלאה בכל נושא ‪ .‬ההצדקה לגישה זו נובעת ראשית ‪ ,‬כדי למנוע‬ ‫פגיעה באנשים ‪ ,‬ובכלי השייט שלך ואלה שבשכנות אליך ‪ .‬שנית ‪ ,‬משום שהפעילות‬ ‫ההפוכה ‪ ,‬בהרבה מקרים ‪ ,‬מחייבת נגישות למקומות ואמצעים אחרים ממקום‬ ‫הפעולה הראשוני‪.‬‬ ‫לבוש מתאים ‪ ,‬חלוקת תפקידים ועמדות‪ ,‬קיום סדר בכלים וחבלים ‪ ,‬וציות לפקודות‬ ‫על ידי חזרה על פקודות ואשור בצוע ‪ ,‬כל אלה הם הבסיס למניעת פגיעות ותקלות‬ ‫וגם ל הנאה מעבודת צוות ‪.‬‬ ‫הערנות ‪ ,‬ההרגלים והמיומנויות אינם נשמרים אלא אם חוזרים ומתנסים בהם ‪.‬‬ ‫אל תחתור רחוק יותר משתוכל לחזור‬ ‫השפה של הפיזיקה והמקצועות הטכנולוגיים‬ ‫( הגדרות בסיס ‪ ,‬מידע רקע לכל מקצועות השיט ‪).‬‬ ‫בלמוד עקרונות של תורת השיט ‪ ,‬בספרות ההדרכה ובלשון המרצים ‪ ,‬חוזרים ופוגשים שני‬ ‫מושגים ‪ ,‬בסיסיים ‪ -:‬זוית ו‪ -‬וקטור ‪.‬‬ ‫גם אם לא למדת מושגים אלה במסגרת כל שהיא ‪ ,‬המשך לקרא ‪ ,‬כאן המקו ם להתחיל ‪ ,‬או‬ ‫להבין את מה שכבר בצעת וראית‪ ,‬או מה שלא הופנם בהכרתך ‪.‬‬ ‫בלימודי מתמטיקה ופיזיקה מקובל להגדיר כל מושג ‪ ,‬שהוא חדש ללומד ‪ ,‬לפני‬ ‫שמשתמשים בשמו להגדרות אחרות ‪ ,‬לדוגמה ‪ ,‬מגדירים " נקודה " לפני " קו " ‪ ,‬וקו לפני‬ ‫" מישור " וכיו " ב ‪ .‬בפרק זה לא תנתנה ההגדרות הראשוניו ת‪ ,‬אלא רק בהקשר שזה משמש‬ ‫את למוד הימאות ‪ ,‬ובהסתמך על ' תפישתו החוויתית' של הקורא – לדוגמה כאשר כתוב‬ ‫" מישור " ההנחה היא שהקורא מבין שמדובר ‪ -:‬בפני הים ‪ ,‬בדף שרטוט ‪ ,‬מפה ימית או כל‬ ‫חתך דו‪ -‬ממדי‪ .‬כמו כן ‪ ,‬ההנחה היא ‪ ,‬שלקורא הכרה מסויימת של פעולות השיט ‪ ,‬ויודע‬ ‫שניווט הו א מציאת אתרים ונתיבים; ואילו ניתוב הוא תכנון ועצוב התנועה של כלי השיט‬ ‫בנתיבים שבין אתרים ‪ ,‬ומבין מהם‪ :‬תמרון ‪ ,‬עגינה ורתוק ( או רתיקה ) ‪.‬‬ ‫ההסברים מובאים בהנחה ‪ ,‬שהקורא יכול להסביר לעצמו את הפעולות‪ -:‬חבור ‪ ,‬חסור ‪ ,‬כפל‪,‬‬ ‫חלוק ‪ ,‬העלאה בחזקה והוצאת שורש ‪ .‬ישנה חשיבות גם להבנה של המושגים " חיבור‬ ‫אלגברי " " חיבור וקטורי " והכרת ההבדל בין " זהות " ‪ " ,‬שוויון " ‪ " ,‬משוואה " ו " תלות‬ ‫מתמטית " ( פונקציה) ‪ ,‬ובצוע פעולות כמו שינוי נושא בנוסחה‪ ,‬ו " ערך משולש " ; אך אלה‬ ‫יוסברו במקומות שיעזרו להבנה‪.‬‬ ‫רוב המורים וספרי ההדרכה בנושאים טכנולוגיים ‪ ,‬כמו השיט ‪ ,‬פוסחים על מונחי היסוד‬ ‫בהסתמכם על השכלת רקע של הלומד; המורים ‪ ,‬במסגרות הדרכה למיניה ן ‪ ,‬מוגבלים‬ ‫במסגרת זמן ‪ ,‬או שאינם מכירים בחשיבות הדיוק בשפה ‪ .‬כתוצאה מכך ‪ ,‬לרוב הלומדים אין‬ ‫כלים וסבלנות ‪ ,‬להתעכב ולהבין את כוונ ת כל ביטוי ‪ .‬ובעובדה ‪ ,‬מתקיים מצב‪ ,‬שמילים‬ ‫ובטויים מובאים לשמוש שגוי ‪ ,‬ואפילו במשמעויות מנוגדות לכוונת המקור ‪ .‬להמחשה‪-:‬‬ ‫לשאלה מה הם שלושת המימדים המרכיבים את ה " עולם הפיזיקלי " ? ראשית יש להבהיר‬ ‫מהו " העולם הפיזיקלי " ( שתורת השיט כלולה בו ) ? והתשובה‪ -‬שהעולם הפיזיקלי הוא‪:‬‬ ‫תורת הפיזיקה והישום שלה בהנדסה ובניה ‪ .‬תורת הפיזיקה מורכבת מ‪ -‬א ) חקירה מהותית‬ ‫של תופעות ‪ .‬זו חקירה שנותנת הסבר ושמוש צפוי לתופעות שמגלה האדם החוקר ‪ .‬ב )‬ ‫חקירה כמותית‪ .‬זו חקירה שמגדירה גדלים ומרכיבה נוסחאות ‪ ,‬כדי לאפשר למהנדסים‬ ‫והבנאים ‪ ,‬במדידות וחישוב כמויו ת ‪ ,‬להביא לשמוש את התופעות שנחקרו‪.‬‬ ‫מה הם שלושת המימדים המרכיבים את ה " עולם הפיזיקלי " ? צפוי שרוב הקוראים‬ ‫ישיבו " אורך ‪ ,‬רוחב וגובה " ובכן לא! שלושת אלה הם אותו מימד – מימד של אורך ‪ .‬גם ‪-‬‬ ‫אורך ‪ ,‬שטח ונפח הם אותו מימד ‪ ,‬שכן אורך הוא אורך בחזקת אחת ‪ ,‬שטח הוא אורך ברבוע‬ ‫ונפח הוא אורך בחזקה שלישית ‪ ,‬כלומר בוצעה פעולה אלגברית על אותו מימד ‪ .‬אם כך‬ ‫מהם המימדים שמשמשים עמודי יסוד לתורת הפיזיקה ? התשובה המצומצמת היא אורך‬ ‫‪ , Length= L‬מסה =‪ , Mass M‬וזמן ‪ . Time= T‬ולשימושים נוספים מוגדר גם המטען‬ ‫החשמלי של אלקטרון כמימד יסוד ‪ ē‬סימן המינוס מעל ה‪ e -‬בא לסמן שהאלקטרון הוא‬ ‫חלקיק של מטען שלילי ‪.‬‬ ‫כדי להדגיש את משמעותם של ‪ L M T‬כמיצגים מימד יסוד פיסיקלי ‪ ,‬מקובל‬ ‫לכתוב את המימד בתוך סוגריים מרובעים ]‪ . [ ē ] [L] [M] [T‬יש ספור‪ ,‬הגורס‬ ‫שהמילה " יסודות " באנגלית ‪ ELEMENTS‬מקורה במורה או מ ורים שהרבו להשתמש‬ ‫באותיות אלה ‪ -:‬אל – אמ‪ -‬אנד טי וכך בשגרת ההגוי הפכו האותיות למילה שמשמעותה‬ ‫" יסודות "‪ .‬כהמשך לכך ‪ ,‬תופעות היסוד בטבע ‪ ,‬שמשפיעות על מזג האווי ר ‪ ,‬אף הן מכונות‬ ‫באנגלית ‪. THE ELEMENTS‬‬ ‫ההגדרה המדעית של כל אחד מאלה היא מורכבת ובעיתית ‪ ,‬אם נזהרים שלא להשתמש‬ ‫במושגים שאינם מכילים את המימד עצמו ‪ .‬תנתן כאן הגדרה חופשית‬ ‫ועממית ‪-:‬‬ ‫]‪ – ] L‬אורך הוא רצף של נקודות שונות‪ ,‬שמתחיל בנקודה קבועה ומסתיים‬ ‫בנקודה ‪ ,‬קבועה ( מהי נקודה ? )‪.‬‬ ‫]‪ – ] M‬מסה היא תכונתו של גוף ( מהוא גוף ? ) להתנגד לשנויים במצבו‬ ‫( כמות ‪ /‬צפיפות החלקיקים שמרכיבים את הגוף ומחזיקים אותו‬ ‫בצורתו ‪ /‬בנפח נתון )‪.‬‬ ‫]‪ – ] T‬זמן הוא ההבדל בהתרחשות של ארועים ‪ .‬את האירועי ם אנו דוגמים‬ ‫בחושינו השונים ובזיכרוננ ו ( מה עם אירועי ם שאיננו חשים או זוכרים ? ) ‪,‬‬ ‫כך אנו קובעים " התחלה " ‪ " ,‬סוף " ו " פרקי זמן "‪.‬‬ ‫[ ‪ – ] ē‬מטען חשמלי הוא תכונה של חלקיק חומר להדחות או להמשך על ידי‬ ‫חלקיקים אחרים ‪ .‬תכונה זו מקבלת שמות שונים בתורות שונות של הפיזיקה‬ ‫האטומית ( גרעינית )‪ .‬בהיסטוריה של חקירת הזרם החשמלי הסתבר‪,‬‬ ‫שהאלקטרונים נעים הפוך למה שהוסכם ‪ ,‬ככוון הזרם ממקורותיו ‪ ,‬ולכן הסימן‬ ‫מינוס (‪ ) -‬מעל ה‪. ē -‬‬ ‫למה זה חשוב ? למי ששואל התשובה היא ‪ -:‬כי זה טוב לדעת! אך גם למניעת בלבול‬ ‫מושגים וטעויות בפתרון בעיות ‪ ,‬ו כדי לזהות ‪ ,‬שה פתרון אכן נכון גם במימד וביחידות ולא‬ ‫רק בתוצאה המספרית‪.‬‬ ‫להלן הסבר ‪ ,‬ברצ ף מתפתח‪ ,‬לסימונים ואותיות שיבואו לשימו ש בפרקים הבאים ‪-:‬‬ ‫‪ . 1‬אורך ‪ /‬מרחק ‪Distance‬‬ ‫כאשר אנו מוצאים ש המרחק בין שני אתרים הוא ‪ 15‬מילים ימיים אנו כותבים ‪-:‬‬ ‫‪ = Distance = D= 15 nm‬שם הגודל ומה כלול בכיתוב זה ?‬ ‫‪ - D‬הוא קיצור‪ /‬סימון לשם הגודל מרחק ‪. Distance -‬‬ ‫המימד של מרחק הוא אורך ‪.] L [ 1‬‬ ‫= הוא הסימן המתמטי לשוויון‪.‬‬ ‫‪ – 15‬הוא מספר דו‪ -‬ספרתי‪ ,‬ולכן הוא " שלב " בסולם שבין ‪ 11‬ל‪ , 111 -‬כלומר‪:‬‬ ‫" סדר גודל של עשרות " ( כשהבסיס ל " סדרי‪ -‬הגודל " הוא כפולות של ‪.)11‬‬ ‫‪ – nm‬זה ה סימון של היחידות בהן בחרנו למדוד את האורך – ‪. Nautical Miles‬‬ ‫‪ – Nautical Miles‬הוא ה כנוי של היחידות בהן בחרנו למדוד את המרחק‪,‬‬ ‫בשונה מ‪ :‬מטרים ‪ ,‬רגל ‪ ,‬מעלות ‪ ,‬ועוד כיו " ב ‪.‬‬ ‫החל מכאן ‪ ,‬בכל שמוש בגודל פיזיקלי ‪ ,‬ראוי שתזהה את המציינים הנלווים ‪-:‬‬ ‫שם הגודל ‪ ,‬קיצור מקובל ‪ ,‬סדר גודל שבשמוש ‪ ,‬סימון היחידות בכתב ‪ ,‬כנוי היחידות‪,‬‬ ‫ההרכב של הגודל על ידי שימוש רק במימדי היסוד ‪. LMT‬‬ ‫תרגיל דוגמה להמחשת השמוש במציינים הנ " ל ( מודגשים באדום )‪-:‬‬ ‫משיט מתכנן לצאת עם ספינתו ‪ ,‬ממרינה הרצליה למרינה לרנקה בקפריסין‪ ,‬המרחק במפה‬ ‫הימית ‪ ( 175nm‬מילים ימיים )‪ .‬כמה ליטרים דלק עליו לשאת ‪ ,‬כדי להגיע ליעד?‬ ‫נתונים לחישוב‪:‬‬ ‫‪ . 1‬כשמטרת השיט אינה " מבצע שהצלחתו הכרחית " ‪ ,‬ההגיון נותן ‪ ,‬שכדאי לתכנן‬ ‫למקרה הגרוע ביותר ‪ ,‬אך לא כדאי להשקיע בתכנון למקרים קיצוניים של " כח‬ ‫עליון "‪.‬‬ ‫‪ . 2‬מבחינת " ימאות טובה " מקובל לשאת לפחות ‪ 25%‬עודף דלק ‪ ,‬מעל לכמות שחושבה‬ ‫כהכרחית ‪.‬‬ ‫‪ . 3‬נבחר ב " מהירות השיוט " של כלי השיט‪ ,‬בטעינה ו שוקע תקניים ‪ ,‬ובמספר סיבובי ציר‬ ‫( סל " ד ) ‪ ,‬שמומלץ על ידי היצרן‪ ,‬ובים שקט ‪ ,‬כ‪ ( 7Knt -‬קשר מיל ימי בשעה )‪.‬‬ ‫‪ . 4‬מקובל שצריכת הדלק של מנוע דיזל היא כ‪ 181 -‬גרם בכל שעה של פעולת מנוע ‪,‬‬ ‫לכל כח‪ -‬סוס של הספק המנוע ‪.‬‬ ‫‪ . 5‬דלק‪ -‬סולר קל מהמים ‪ ,‬וצפיפותו ( יחידות משקל ליחידת נפח) היא ‪ 1.8 4‬ביחס למים‬ ‫( ישנם דלקי‪ -‬סולר שצפיפותם ‪) 0.88/0.87‬‬ ‫‪ . 6‬נניח שנפח מיכלי הדלק של הספינה ‪ 121‬ליטר ‪.‬‬ ‫‪ . 7‬בספר המנוע ובתעודת " כושר השיט " של הספינה כתוב שהספק המנוע ‪24Kw‬‬ ‫( קילו‪ -‬ווט )‪.‬‬ ‫‪ ( 1hp . 8‬כח סוס ) הוא הספק של כ‪ 736 Watts -‬וו ט ‪.‬‬ ‫פתרון‪-:‬‬ ‫א ‪ .‬מספר שעות הצפוי לפעולת מנוע ‪ ,‬הוא המרחק מחולק במהירות ‪ 25h‬‬ ‫ב ‪ .‬הספק המנוע ב " כוחות סוס " יהיה ‪ ,‬לאחר הפיכת ‪ 24Kw‬ל‪,24.000w -‬‬ ‫‪175nm‬‬ ‫‪7kts‬‬ ‫‪.‬‬ ‫‪24000‬‬ ‫‪ 32HP‬‬ ‫‪736‬‬ ‫ג ‪ .‬בכל שעה צורכים ‪ 181‬גרם לכל ‪ 181 , 1HP‬גרם הם ‪ 1,18‬קילו‪ -‬גרם ‪ ,‬ולכן‬ ‫התצרוכת ל‪ 1 -‬שעה תהיה ‪ 0,18‬ק " ג ‪ 32 X‬כ " ס = ‪ 5.76‬ק " ג סולר בשעה‪.‬‬ ‫ד ‪ .‬אנו מעונינים להפוך את יחידות הצריכה מק " ג לליטר ‪ ,‬משום שהדלק מסופק ‪,‬‬ ‫ומחירו נקוב לנו ‪ ,‬ביחידות נפח ולא ביחידות משקל ‪ .‬כפי שנתון לעיל‪ ,‬צפיפות‬ ‫( ק " ג לליטר ) הסולר קטנה מצפיפות המים ‪ ,‬ביחס של ‪ , 1.8 4‬לכן ‪ 5.76‬ק " ג‬ ‫‪5.76‬‬ ‫סולר יתפסו נפח ג דול יותר של ‪ 6.86  7 lit.‬‬ ‫‪0.84‬‬ ‫ל‪ 25 -‬שעות מנוע יהיו דרושים ‪ 7‬ליטר ‪/‬שעה ‪ 25 X‬שעות = ‪ 175‬ליטר ‪.‬‬ ‫‪175‬‬ ‫ה‪ .‬היות ומעונינים בעתודה של ‪ 25%‬יש להוסיף ¼ מהכמות כלומר‬ ‫‪44 ‬‬ ‫‪4‬‬ ‫ליטר ‪ ,‬ונצטרך למלא ‪ 224 = 181 + 44‬ליטר ‪ .‬היות והמיכלים של הספינה‬ ‫בנויים ל‪ 121 -‬ליטר ‪ ,‬נזדקק לתוספת מיכל או מיכלים של ‪114 = 121 – 224 -:‬‬ ‫ליטר ‪ .‬לסיכום ציטוט כלל אצבע ‪-:‬‬ ‫‪Use the old rule of thumb; Use one-third of the fuel in your tank to get there, one‬‬‫‪third to get back and save the last third as an emergency backup .‬‬ ‫‪ . 2‬מהירות ‪Velocity‬‬ ‫כשאנו מוצאים שמהירות כלי השיט היא ‪ 7‬מילים ימיים בשעה אנו כותבים ‪-:‬‬ ‫‪ Velocity = V = 7Kts‬ברישום הימי מקובל הקיצור ‪ SPD‬מהמילה ‪.SPEED‬‬ ‫‪ – V‬מהירות על פי הגדרתה היא דרך שגוף עובר ביחידת זמן‬ ‫לכן המימדים מהם מורכבת המהירות הם אורך חלקי זמן‬ ‫את האורך ‪ , L‬בים ‪ ,‬בחרנו למדוד ביחידות של מילים ימיים ‪ ; n.m.‬את הזמן ‪ T‬בחרנו‬ ‫למדוד ביחידות של שעות ‪ . Hours=h‬הערכים המספריים של ‪ ) Distance ( L‬ו‪T -‬‬ ‫נבחרים ומחושבים מתוך סולם שמתאים לשמוש ‪.‬‬ ‫כלומר ‪ ,‬לא נבחר להביע את המרחק באלפיות של מטר ( מילימטרים ) ואת הזמן בשנים ‪,‬‬ ‫זאת כדי שהכיתוב לא יהיה מרובה ספרות לפני ואחרי הנקודה העשרונית ‪ .‬גבולות הסולם‬ ‫בו אנו בוחרים להשתמש‪ ,‬הוא " סדר הגודל "‪ .‬משתדלים לבחור סדרי גודל כך שהכיתוב‬ ‫של ערכים יהיה במספר קטן של ספרות ‪ .‬בדוגמה שלפנינו ‪ 7‬קשר הוא בסולם שבין ‪ 1‬ל‪11 -‬‬ ‫כלומר סדר גודל של יחידות ‪ ( ,‬בסעיף ‪ 15 , 1‬מיל ימי סדר הגודל הוא בין ‪ 11‬ל‪ 111 -‬כלומר‬ ‫סדר‪ -‬גודל של עשרות )‪.‬‬ ‫כאן ‪ ,‬בתורת השיט ‪ ,‬במקום לכתוב‪ " :‬מילים ימיים בשעה " מכנים את יחידת המהירות‬ ‫" קשר " ‪ KNOTS‬וסימון היחידות הוא ‪. KTS‬‬ ‫למרות שהאורך והזמן הם גדלים שנוקבים את ערכם מתוך סולם של ערכים ‪ ,‬כלומר הם‬ ‫גדלים המכונים " גדלים סקאלריים " ( סולמיים ) ‪ ,‬החלוקה של אורך בזמן אינה גודל סקאלרי‬ ‫טהור ‪ .‬על פי מהות ההגדרה ‪ ,‬המהירות של גוף היא בכוון מסויים ‪ ,‬ולכן חייבים לציין את‬ ‫כוון התנועה במהירות הנד ונה ‪ .‬מצורך זה ‪ ,‬נובע מושג חדש‪ " -‬גודל וקטורי " ‪ .‬כל גודל‬ ‫שקשור בכוון מכונה " גודל וקטורי "‪ .‬לשמושים מסוימים‪ ,‬כאשר הכוון משתנה עם הזמן ‪,‬‬ ‫משתמשים בכנוי " פאזור " במקום " וקטור " ‪.‬‬ ‫בנתינת ערכו של גודל וקטורי חייבים לתת בו זמנית את מספר היחידות ‪ ,‬מתוך סולם‬ ‫נבחר ‪ ,‬ואת הכוון ‪ .‬פעולות החישוב שבין וקטורים ‪ ,‬או בין וקטורים וגדלים סקאלריים ‪ ,‬שונות‬ ‫מאשר הפעולות האלגבריות של חסור‪ ,‬חבור כפל וחלוק במספרים ‪.‬‬ ‫אם לא נדע את כללי האלגברה ביחס לווקטורים ‪ ,‬לא נוכל להבין את פעולת הרוח על‬ ‫מפרש; את פעולת המים על לוח ההגה ‪ ,‬את פעולת המדחף על ה מים; את נתיב כלי השיט‬ ‫בזרם; את המתיחות בחבלים וכבלים ועוד כיו " ב ‪ .‬לצורך פתרון בעיות עם וקטורים נוח‬ ‫אך על כך בהמשך‪.‬‬ ‫להשתמש בשרטוט שבו הוקטורים מתוארים כחיצים‬ ‫‪ . 3‬תאוצה ‪acceleration‬‬ ‫כאשר אנו גורמים לכלי שיט לנוע ממצב נייח ועד למהירות הרצויה ‪ ,‬אנו‬ ‫גורמים לו ל " האיץ "‪ .‬מהות ה " תאוצה " היא תוספת מהירות ביחידת זמן‪.‬‬ ‫תוספת המהירות היא ההפרש בין המהירות ‪ ,‬שהגענו אליה בסוף יחידת הזמן‪,‬‬ ‫לזו שהיינו בה בתחילת יחידת הזמן ‪.Δt =t-t 0‬‬ ‫‪ Δ‬מסמן הפרש בין שני ערכים ‪.Difference‬‬ ‫כותבים גם ‪ V t ± V 0‬כדי לכלול את המקרה של תאו צה שלילית כלומר " תאוטה " בעצירה ‪.‬‬ ‫התאוצה ‪ a‬אינה שמושית לשיט בסיסי‪ ,‬וגם אינה פשוטה למדידה ‪,‬‬ ‫אך היא משמשת להגדרות חשובות יותר ‪.‬‬ ‫מימדיה של התאוצה מורכבים מהפרש מהירות ‪ ΔV‬חלקי זמן ‪ . t‬היות והפרש של‬ ‫מהירויות אף הוא מהירות ‪ ,‬המימדים יהיו‪ :‬אורך חלקי זמן ברבוע‬ ‫לתאוצה אין סמל יחידות וכנוי יחידות אלא רושמים ואומרים את יחידות המרחק חלקי‬ ‫יחידות הזמן ברבוע‪ ,‬את התאוצה הנגרמת ממשיכת כדור הארץ מסמני ב‪ g -‬במקום ב‪. a -‬‬ ‫ישנה שגיאה נפוצה בין " עכברי יבשה " ‪ ,‬שמביעים את מהירות הרוח ב‪ " -‬קשר לשעה "‪.‬‬ ‫לדוגמה ‪ " 21‬קשר לשעה "‪ .‬זו שגיאה ה יות וקשר הוא הכנוי ליחידת מהירות של מילים‬ ‫ימיים בשעה ‪ " 21 .‬קשר לשעה " אומר שכל שעה מהירות הרוח גדלה ב‪ 21 -‬קשר‪ ,‬וזו ‪,‬‬ ‫כמובן ‪ ,‬תאוצה די מפחידה ‪...‬‬ ‫‪ . 4‬כח ‪FORCE‬‬ ‫כאשר אנו מותחים מפרש אנו גורמים לרוח להפעיל עליו כח‪ ,‬כאשר אנו מפעילים מנוע‬ ‫ומשלבים מדחף אנו מעתיקים את כח המנוע לכח דחף במים ‪ ,‬כך גם עם פעילויות רבות‬ ‫אחרות ‪ .‬מהו כח ? לפי דוגמאות אלה ‪ ,‬הכח הוא הסיבה שגוף ישנה את מצבו ‪ ,‬ובמקרה‬ ‫שהגוף עובר ממנוחה לתנועה ‪ ,‬הרי הוא מאיץ ממהירות אפסית למהירות בערך כל שהוא‪.‬‬ ‫ולכן הכח מו גדר כמכפלה של תאוצה במסה ‪ .‬וכותבים ‪ . Force = F = m x a -:‬מסה היא‬ ‫גודל " סקאלרי " ואילו התאוצה היא " גודל וקטורי " ‪ ,‬ובמקרה זה יוצא שגם הכח הוא " גודל‬ ‫וקטורי "‪ .‬זה מוביל לכך שיש לציין את כוון הכח ‪ ,‬ולפתור בעיות בנדון השפעת כוחות‪,‬‬ ‫בכללי מתמטיקה של ווקטורים ‪.‬‬ ‫מהוא המימד של כח ?‬ ‫היחידות שמשמשות למדידת מסה הן גרם‪ -‬מסה או ק " ג‪ -‬מסה ‪ ,‬התאוצה שמקבלת מסה ‪,‬‬ ‫מכח המשיכה של כדור הארץ ‪ ,‬בכוון מרכזו ‪ ,‬היא ‪ 8.8‬מטרים בשניה ברבוע ‪ ,‬ובמקום ‪a‬‬ ‫מקובל לסמנה ב‪ , Gravity = g -‬וזו מכונה " התאוצה הארצית " ‪ " .‬שדה הכבידה" של כדור‬ ‫הארץ הוא המרחב שבו מורגשת פ עולת כוחות על מסות שגורמים להן לתאוצה של‬ ‫‪ g=9.8m/s 2‬בכוון מרכז הכדור ‪ .‬חשוב להבחין ‪:‬‬ ‫א ) המסה של גוף אינה משתנה על על כדור הארץ ‪ ,‬ולא בכל מקום אחר במרחב ‪ ,‬ואף לא‬ ‫אם יהפוך מוצק לפרורים או לנוזל או לגאזים ‪.‬‬ ‫ב ) אם נכפיל את התאוצה הארצית במסה של גוף נקבל את מה שמכ ונה " משקלו " של‬ ‫הגוף במקום בו הוא נמצא ‪ ,‬כלומר כח ‪ F‬ביחידות של ק " ג‪ -‬כח או " ק " ג‪ -‬משקל " ‪ ,‬ואלה‬ ‫שונות מק " ג‪ -‬מסה ‪.‬‬ ‫ג ) כאשר יש לחשב כמויות ‪ ,‬בוחרים מערכת יחידות מוסכמת‪ ,‬שמתואמת לאותו נושא‬ ‫שעוסקים בו ‪ .‬לדוגמה בשיט תחרותי עכשווי יש שימוש למדידת מהירות ביחידות של‬ ‫" אורכי‪ -‬סירה " ‪ .‬בהשוואת המהירות של שתי סירות מתחרות ‪ ,‬אומרים שהאחת מהירה‬ ‫מהשניה ב " ‪ 3‬אורכי סירה " ולא ב‪ 4 -‬ק " מ לשעה‪ ,‬או ב‪ 2 -‬קשרים ‪ .‬בשלבי הלמוד ‪ ,‬ובשימושים‬ ‫נפוצים מקובל ‪ ,‬לחשב במערכת המכונה " מערכת יחידות ‪ . " MKS‬במערכת זו מבטאים‪:‬‬ ‫אורכים ‪ [L] -‬במטרים ‪ ,‬מסה ‪ [M] -‬בק " ג ( אלפי גרמים ) ‪ ,‬וזמן – ]‪ [T‬בשניות ‪ .‬במערכת זו‬ ‫הכח ‪ F‬נמדד ביחידות המכונות ניוטון ‪ ,‬על שם הפיזיקאי ‪ , Newton‬נפוצה גם מע רכת‬ ‫דומה המכונה " מערכת מדעית בין‪ -‬לאומית " ההבדל אינו משמעותי לדיון כאן‪.‬‬ ‫ד ) השוני בין ‪ 1‬ק " ג מסה ל‪ 1 -‬ק " ג כח ‪ /‬משקל תלוי בתאוצה‪ .‬כאשר משתמשים במילה‬ ‫" משקל " מתכונים לכך שכח המשיכה של כדור הארץ פועל על על המסה וגורם לה לנפילה‬ ‫בתאוצה של ‪ m/s 2 8.8‬או אם אינה נעה אלא ני יחת ‪ ,‬היא מפעילה כח של‪ 1 -:‬ק "ג‪ -‬מסה ‪x‬‬ ‫‪ 1 = m/s 2 8.8‬ק " ג כח ‪ .‬מקובל להגדיר משקל על פני כדור הארץ ‪, Weight = W= m xg‬‬ ‫אם נעגל ‪ 8.8‬ל‪ 11 -‬נקבל ש ‪ 1‬ק " ג משקל = ‪ 11‬ניוטון ‪.‬‬ ‫לסכום‪ :‬כח ‪ F‬הוא מכפלה של מסה בתאוצה; הכח הוא " גודל וקטורי " והוא נמדד ביחידות‬ ‫" ניוטון " במערכת ‪. MKS‬‬ ‫הערה למשיט‪ :‬ב ספרות ההדרכה ובשאלונים נתקלים בשמוש בביטויים " עצמת הרוח " או‬ ‫" עצמת הזרם " ‪ " .‬עצמה " משמעותה כח ‪ ,‬ואינה נמדדת ביחידות " קשר " או ק " מ בשעה ‪.‬‬ ‫המהירות והכח שניהם גדלים וקטוריים אך הם שונים כפי שהוסבר לעיל ‪ .‬לכן ‪ ,‬כדי לדייק ‪,‬‬ ‫היה ראוי להתיחס ל " מהירות הרוח " ו " מהירות הזרם " ‪ ,‬ולזכור ששני אלה נמדדים‬ ‫ביחידות " קשר " או ק " מ בשעה ‪ ,‬ולא ב " ניוטון " או ק " ג‪ -‬כח ‪ .‬אילו רצינו למדוד את " עצמת "‬ ‫הרוח או הזרם ‪ ,‬היינו נדרשים להתיחס ליחידת שטח ‪ ,‬של כלי השיט או מפרש ‪ ,‬או ליחידות‬ ‫תאוצה ‪ ,‬שמושפעים מפעולת הכח‪.‬‬ ‫‪ . 5‬עבודה ‪ENERGY / WORK‬‬ ‫הפעולה של כח לאורך דרך ‪ /‬מרחק מכונה עבודה ‪ , W=FxS‬אך העבודה היא גודל פיסיקלי ‪,‬‬ ‫שיכול להיות אגור ‪/‬צבור ‪ /‬מאוחסן בתוך חומרים ומתקנים בצורות שונות‪.‬‬ ‫כאשר יש מאגר שאפשר להפיק ממנו עבודה ‪ ,‬במקום " עבודה " משתמשים במילה אנרגיה‬ ‫‪ .‬במערכת ‪ MKS‬יחידות העבודה מכונות ג ' אול ‪ , Joules‬המאגר ‪ ,‬שבו שמורה היכולת‬ ‫לבצע עבודה ‪ ,‬נקרא " מקור‪ -‬אנרגיה "; וכדי להפיק את העבודה הרצויה ממקור אנרגיה יש‬ ‫לבצע פעולה המכונה " המרת‪ -‬אנרגיה " והמתקן המבצע את ההמרה יכול לקבל שמות‬ ‫שונים ‪ .‬נקדים ‪ ,‬שבכל המרת אנרגיה ישנם הפסדים‪,‬‬ ‫ועובדה זו הובילה להגדרת מושג ה " נצילות " על כך בהמשך‪ .‬הממירים השונים מכתיבים‬ ‫גם יחידות שונות להערכת העבודה‪ ,‬לדוגמה כאשר ממירים חומרי דלק לחום העבודה‬ ‫נמדדת ב " קלוריות " ולא כהכרח ב‪ -‬ג ' אול ‪ ,‬יחידת‪ -‬חום היא בקרוב ‪ 4.2‬ג ' אול לכל קלוריה ‪,‬‬ ‫במזגנים פוגשים ביחידות ‪ B.T.U‬שהן " יחידות טרמיות בריטיות " כשהיחס הוא ‪1 BTU‬‬ ‫‪ . =252 Cal‬להלן מספר מתקנים שכוללים ממירים עם שמות נפוצים ומוכרים‪ :‬מקרן‪-‬‬ ‫חום ‪ /‬רדיאטור ‪ ,‬אנטנה ‪ ,‬מחולל‪ -‬חשמלי ‪ /‬גנרטור ‪ ,‬מנועי קיטור‪ ,‬דיזל ובנזין ‪ ,‬תאים וסוללות‬ ‫מצברים ‪ ,‬שנאים ‪ /‬טרנספורמטורים ועוד כיו " ב ‪.‬‬ ‫העבודה ‪ W=FxS‬היא מכפלה של גודל וקטורי ( כח ) בג ודל סקאלרי ( דרך ) ‪ ,‬אך היא בעצמה‬ ‫גודל סקאלרי והמימדים שלה הם ‪-:‬‬ ‫‪ . 6‬הספק ‪POWER‬‬ ‫ההספק הוא כמות העבודה שמתבצעת ביחידת זמן ‪-:‬‬ ‫את ההספק ‪ ,‬במערכת ‪ MKS‬מודדים ביחידות המכונות‬ ‫‪ Watt‬או אלפי ווטים ‪ , KW‬כש‪ = 11 3 = K -‬סדר גודל של אלפים ‪.‬‬ ‫המימדים של ההספק הם ‪-:‬‬ ‫את עצמתם של מנועים נהוג לנקוב ביחידות של הספק ‪ = KW‬קילו‪ -‬ווטים או‬ ‫‪ " Horse- Power = HP‬כחות סוס "‪ ,‬כאשר ‪ 1‬כ " ס = ‪ 746‬ווט ‪.‬‬ ‫יש לשים לב לכך שחברות המספקות חשמל ‪ ,‬בין למגורים ‪ ,‬ובין לכלי שיט הרתוקים לרציף ‪,‬‬ ‫מה שמכונה " חשמל חוף " ‪ ,‬נוקבות את העלות של השמוש ביחידות ה מכונות ‪= KWh‬‬ ‫" קילו‪ -‬ווט ‪ x‬שעה " ‪ ,‬ואלו אינן יחידות הספק ‪ ,‬אלא יחידות עבודה ‪ ,‬שכן אם נשנה את נושא‬ ‫נוסחת ההספק שלעיל נקבל ‪ W=Pxt‬כלומר‪ -‬הספק ‪ X‬זמן = עבודה ‪ .‬זאת ‪ ,‬משום שאת‬ ‫ספקי האנרגיה לא מענין בכמה זמן צרכנו אותה‪ ,‬אלא איזה חלק מהמאגר שלהם צרכנו ‪,‬‬ ‫ועל כך יגבה המחיר‪ .‬כאשר אנו רוכשים מכשור ‪ ,‬שצורך אנרגיה ‪ ,‬ראוי שנחשב ‪ ,‬לפני‬ ‫הרכישה ‪ ,‬באם יש ברשותנו ספק אנרגיה מתאים ובאם העלות הכספית מוצדקת‪ ,‬ויש לנו‬ ‫את התקציב הכספי עבורה‪.‬‬ ‫תרגיל של חישוב עלות חשמל חוף‪- :‬‬ ‫נניח שבכלי השייט אין רשת צרכנים שפועלת ישירות מחשמל חוף במתח חילופין‪ ,‬אלא‬ ‫ישנה יחידת המרה ומיתוג ‪ ,‬שמזינה את הרשת ‪ 12V‬זרם ישר ‪ ,‬של כלי השייט‪ .‬הנחה זו‬ ‫באה היות ויש כלי שייט ‪ ,‬שמותקנות בהם יותר מרשת אחת ‪ ,‬ובכל רשת ‪ ,‬צרכנים משלה ‪.‬‬ ‫לדוגמה ‪ :‬רשת צרכנים ‪ 220V‬בזרם חילו פין ( תאורה‪ ,‬מזוג אויר ‪ ,‬מקרר ‪ /‬בר‪ ,‬חמום מים ‪,‬‬ ‫תנורי בישול וכל צורך חופי )‪ .‬רשת חשמל ל " צרכנים בזמן חרום " – שניזונ ה ממצברים‬ ‫מיוחדים לה ‪ 12 ,‬או ‪ 24V‬זרם ישר )‪ , ) DC‬והרשת ה " שגרתית " בזמן שייט ‪ ,‬בדרך כלל‬ ‫‪. 12VDC‬‬ ‫תאור ת ' חללי מחיה ' ( מגורים ‪ ,‬סלון ‪ ,‬מטבח ‪ ,‬שרותים ‪ ,‬שולחן מפות ) נניח ‪ 21‬נורות בהספק‬ ‫‪ 6W‬כל אחת נקבל ‪. 6Wx20 = 120W‬‬ ‫מקרר שצורך כ‪ 8 -‬אמפר ב‪ 12 V -‬הוא בהספק ‪. 86 W‬‬ ‫‪ 2‬אורות סיפון ואור ל " עמדת שליטה " ושולחן אוכל חיצוני ‪ 15W‬כל נורה‬ ‫‪. 15Wx3 = 45W‬‬ ‫‪ 2‬מאווררים של ‪ 20W‬כל אחד ‪. 40W‬‬ ‫אלה הם הצרכנים שיפעלו מירב הזמן ‪ ,‬אך נתן להוסיף צרכנים ‪ ,‬שיפעלו תקופות קצרות ‪,‬‬ ‫כמו בבקורת של חלל מנוע‪ ,‬מנורה ניידת ‪ ,‬תאורת תאי אכסון ואחרים ‪ .‬לטובת כל אלה‬ ‫נוסיף ‪. 15W‬‬ ‫נסכם את ההספקים להספק כללי ונקבל ‪120W+96W+45W+40W+15W = 396W‬‬ ‫לנוחיות נעגל למעלה ל‪. 0.4KW = 400W -‬‬ ‫בעת כתיבת תרגיל זה ‪ ,‬המחיר של ‪ 1000W‬הנצרכים במשך שעה ( ‪ , (1KWh‬ישירות‬ ‫מהרשת ( ‪ (220V AC‬של חברת החשמל הוא כ‪ 1.5 -‬שקל‪ .‬ב הנחה שהצריכה הממוצעת‬ ‫נמשכת כ‪ 6 -‬שעות ביממה ‪ ,‬הרי שהצריכה היא‪-:‬‬ ‫‪ , 0.4KW x 6hours = 2.4KWh‬והעלות תהיה ‪ 1.5 x 2.4KWh‬שקל = ‪ 1.2‬שקל ‪.‬‬ ‫אלא ‪ ,‬שהוצב תנאי שישנה יחידת המרה ומיתוג ‪ ,‬שמזינה את רשת הספינה‪ 12V ,‬זרם‬ ‫ישר ‪ .‬בכל מקרה שבו מתבצעת המרת אנרגיה ישנם הפסדים‪ ,‬כלומר הנצילות של ההמרה‬ ‫אינה ‪. 111%‬‬ ‫בהקשר להספק ה גודל המכונה " נצילות " הוא היחס בין ההספק המופק‪ ,‬ממתקן כל שהוא‪,‬‬ ‫לבין ההספק המושקע בו ‪.‬‬ ‫הספק מופק‬ ‫‪=‬‬ ‫הספק מושקע‬ ‫את הנצילות מקובל לסמן באות היוונית ‪ " ‬אטה " ‪.‬‬ ‫כשאין הפסדים בהמרות האנרגיה ‪ , 1 = ‬אך מצב זה אינן קיים ‪ ,‬ובדרך כלל הנצילות‬ ‫קטנה מ ‪ ,1‬ומקובל להביע אותה באחוזים ‪.‬‬ ‫במקרה של התרגיל הנתון ‪ ,‬אם היחס בין ההספק הנצרך וההספק החשמלי המושקע בו‬ ‫הוא ‪ 1.7‬באחוזים ‪ 111%= 1‬ו‪. = 71% = 1.7 -‬‬ ‫הנצילות היא מספר טהור ללא מימד‪ ,‬משום שהיא יחס בין שני גדלים זהים ‪ ,‬והמימד‬ ‫" מצטמצם " ‪.‬‬ ‫לצורך חישוב העלות ‪ ,‬במקרה הנתון ‪ ,‬יש להוסיף עוד ‪ 31%‬לעלות שחושבה לעיל‪ ,‬אך‬ ‫בדרך כלל ‪ ,‬לא פשוט לחשב מראש את ההפסדים למיניהם ‪ ,‬ופשוט יותר להעריך אותם‬ ‫לאחר שמוש מבוקר‪ .‬כן יש לזכור שהמחיר ל‪ 1KWh -‬שונה משל חברת החשמל במרינות‬ ‫השונות‪.‬‬ ‫משיטים ‪ ,‬נתקלים במושג ההספק‪ ,‬כאשר הם רוכשים כלי שיט או מנוע חדש ‪ ,‬וכאשר הם‬ ‫נדרשים למלא נתונים בטופס בדיקה ראשונית ו תעודת כשירות לרשויות הרישוי ‪ ,‬וכן‬ ‫למנהלות המרינות והמעגנות ‪ .‬הספקי המנועים נתונים על ידי היצרנים על סמך הרצת‬ ‫המנוע כנגד עומס תקני ‪ .‬המספר נקוב ב‪ ( KW -‬אלפי ווטים ) או ב‪ ( HP -‬כוחות סוס) ‪ ,‬ואינו‬ ‫נתון מדויק לחישוב נצילותו ‪ .‬הנצילות תהיה תלויה באיכות ההתקנה ‪ ,‬בסוג המדחף ‪,‬‬ ‫בעומס הכללי שיצרך ‪ ,‬בגודל ‪ ,‬במבנה והטעינה של כלי השיט‪ ,‬ועוד תנאים רבים אחרים ‪.‬‬ ‫‪ . 7‬ריכוז מושגים בחשמל ( המושגים מובאים כאן רק לצורך הכרה ראשונית ובכוונה ‪ ,‬שאפשר יהיה‬ ‫להשתמש בהם בהסב רים ‪ ,‬להגדרות מורחבות ראה חוברת " עזרי ניווט וקשר " עמודים מי‪ 87 -‬עד ‪-‬‬ ‫‪ , 81‬או כל חומר ביסודות החשמל )‪.‬‬ ‫ששת ההסברים עד כאן התיחסו לפרק ‪ ,‬שמכונה " יסודות הפיזיקה " ‪ ,‬ועליו נבנו פרקים‬ ‫אחרים ‪ .‬בכלי שיט פוגשים במתקני חשמל ואלקטרוניקה ‪ ,‬הן לצורך הפעלה ‪ ,‬והן בשלבי‬ ‫ההסמכה‪ ,‬נזקק המשיט להכרת מושגים בתורת החשמל‪ .‬מובאים להלן המושגים‬ ‫היסודיים ‪ ,‬בלי הפרוק למימדים ‪ ,‬אך בהרחבה של הקשר לשמוש הנפוץ ‪-:‬‬ ‫אלקטרון ‪ - ē‬זהו חלקיק במבנה של החומרים השונים ‪ ,‬אשר עצם קיומו ותנועתו נותנים‬ ‫לחומר ולסביבתו תכונות מסוימות‪ .‬התכונות הן בעקר הפעלת כוחו ת וגרימת שינויים‬ ‫בחומר ובסביבתו ‪ .‬המקור לתכונות הוא מה שמכונה " מטען חשמלי " ‪ ,‬כשהמטען של‬ ‫אלקטרון בודד הוא היחידה הקטנה ביותר של התכונות החשמליות שנתן לזהות‪ ,‬וכפי‬ ‫שצוין מתיחסים אליו כמימד הרביעי ]‪. [ē‬‬ ‫ישנו מושג המכונה " אלקטרוניים חופשיים " ‪ ,‬אלה אלקטרונים שאינם חלק ממבנה חומר‬ ‫היסוד ‪ ,‬ונעים בסביבת הגרעין‪ ,‬אלא נעים בתוך החומר ‪ ,‬בהשפעת התנאים בסביבתם ‪ ,‬ונתן‬ ‫לכוונם לבצוע עבודה ‪.‬‬ ‫מטען חשמלי – ‪ Q‬גוף או מקום שיש בו עודף של אלקטרונים ‪ ,‬נאמר עליו שהוא בעל‬ ‫מטען שלילי (‪ ;) -‬גוף או מקום שיש בו חוסר של אלקטרונים ‪ ,‬אומרים עליו שהוא בעל‬ ‫מטען חיובי (‪.)+‬‬ ‫אלקטרונים או חלקיקי‪ -‬חומר טעונים ( פרודות טעונות ‪ /‬יונים ) ידחו ממקום של עודף וימשכו‬ ‫למקום של חוסר כדי להגיע למצב מאוזן ; זאת בדומה לנוזל בכלים שלובים או השקעים‬ ‫והרמות של הלחץ האטמוספרי בתורת מזג האויר ‪.‬‬ ‫ההתפתחות הטכנולוגית אליה הגיע האדם לא הייתה מתאפשרת אילו לא נחקרה תנועת‬ ‫המטענים ‪ ,‬והפיכתה לכלי עבודה ‪ ,‬באין ספור מתקנים המכונים " מתקנים חשמליים "‪ .‬את‬ ‫כמות המטען החשמלי מודדים ביחידות המכונות " קולון "‪.‬‬ ‫שדה חשמלי – ‪ E‬זה המרחב שבו מורגשת פעולת כוחות על מטענים חשמליים ‪ ,‬לדוגמה‬ ‫בין הקטבים של סוללה ‪ .‬שדות חשמליים מתקיימים במ גע ובחיכוך של חומרים שונים הן‬ ‫בינהם והן עם המים והאויר ‪ .‬אי ידיעה של קיומם ‪ ,‬יכולה להיות סיבה לאסונות ונזקים‬ ‫כמעט בכל מקום בכלי שיט שאינו מטופל טפול מונע‪.‬‬ ‫שדה מגנטי ‪ H -‬זה המרחב שבו מורגשת פעולה של כוחות על חומרים הנקראים‬ ‫" חומרים מגנטיים "‪ .‬התכונה המגנטית של חומר היא הפעלת כח משיכה או דחיה של ‪,‬‬ ‫חלקי חומר המכונים " דו‪ -‬קוטב " מגנטי ‪ .‬רב החומרים המגנטים הם סוגים שונים של‬ ‫מתכות ‪ .‬מבחינים ב‪ 3 -‬סוגים עיקריים‪ :‬א ) מתכות שאינן מתמגנטות ולא מושפעות‬ ‫ממגנטים ‪ ,‬כמו עופרת ‪ ,‬אלומיניום ‪ ,‬נחושת ‪ ,‬כסף ‪ ,‬זהב ועוד ‪ .‬אלה נקראות מתכות " דיאה‪-‬‬ ‫מגנטיות "‪ .‬ב ) מתכות שמתמגנטות רק בהיותן בתחום שדה מגנטי ‪ ,‬אך מאבדות את‬ ‫התכונה המגנטית ‪ ,‬כשאינן בשדה ‪ ,‬הן " שוכחות " שהיו מגנטיות ‪ ,‬אלה נקראות " פארה‪-‬‬ ‫מגנטיות "‪ .‬ג ) מתכות שהופכות למגנט לתקופה ארוכה‪ ,‬או כמעט לתמיד‪ ,‬לאחר שקבלו‬ ‫את התכונה המגנטית ‪ .‬אלה נקראות מתכות " פרו‪ -‬מגנטיות "‪ .‬המכשור החיוני והנפוץ ברוב‬ ‫כלי השיט ‪ ,‬מכיל לפחות שמוש אחד בתכונות שתוארו לעיל ‪.‬‬ ‫יחידת מסה מגנטית ‪ M -‬החלקיק הקטן ביותר של חומר ‪ ,‬ששמורה בו התכונה המגנטית ‪,‬‬ ‫של הפעלת כח על מתכות מסויימות‪.‬‬ ‫פוטנציאל חשמלי – ‪ Ua‬הרמה של יכולת לבצע עבודה‪ ,‬עקב עודף א ו חוסר של מטענים‬ ‫חשמליים ‪ .‬הרמה היא בנקודה מסוימת ( או " קוטב ") של שדה חשמלי וברגע מסוים ‪ .‬הרמה‬ ‫נמדדת בנקודה ‪ a‬ביחס לנקודה אחרת ‪ b‬או ביחס ל " אדמה " ' יכולת אפס '‪.‬‬ ‫מתח חשמלי – ‪ Ua-b‬הפרש פוטנציאלים בין שתי נקודות )‪ (Ua-b‬בשדה או במעגל של‬ ‫מוליכים חשמליים ‪ .‬מתח מודדים ביחידות וולט ‪ VOLTS‬על ידי מגע של חיישני המודד‬ ‫בנקודות ‪ a‬ו‪ . b -‬אזהרה ! יכול להתקיים מתח בלי זרם ‪ ,‬אל תחבר את עצמך להיות‬ ‫המוליך של הזרם!‬ ‫זרם חשמלי – ‪ I‬תנועה של מטענים חשמליים בתוך מוליך ‪ ,‬נמדד ביחידות אמפר ‪Ampers‬‬ ‫‪ ,‬לצורך המדידה ‪ ,‬יש לנתק את מסלול הזרימה ‪ ,‬ולחבר את מד הזרם בין קצוות הנתק ‪ .‬אין‬ ‫זרם ללא מתח ‪ .‬אסור לחבר מודד זרם למדידת מתח – זה יוצר קצר!‬ ‫מוליכות חשמלית– ראשית ‪ ,‬כאשר אומרים מוליכות ‪ ,‬מייד מתכוונים גם להתנגדות ולבדוד‬ ‫חשמלי‪ .‬היות ואין ‪ ,‬בטבע הרבה עובדות מוחלטות ‪ ,‬מה שנחשב מבודד בסדרי גודל‬ ‫מסוימים עלול להיות מוליך בסדרי גודל אחרים ‪ .‬אומרים על חומר שהוא מוליך חשמלי‪ ,‬אם‬ ‫יכולה להתקיים בו תנועה של מטענים‪.‬‬ ‫מבחינים בכמה סוגים של מוליכים אך נתייחס רק לשנים‪ :‬א ) מוליכים מסוג ראשון ‪ ,‬אלה‬ ‫המתכות השונות‪ ,‬אשר מאפשרות תנועה של " אלקטרונים חופשיים "‪ .‬ו‪ -‬ב ) מוליכים מסוג‬ ‫שני ‪ ,‬אלה תמיסות ‪ ,‬תערובות או תרכובות של חומרים המאפשרים תנועה פרודות‬ ‫( מולקולות ) חומר טעונות במטען חשמלי ( יונים )‪.‬‬ ‫קצר ונתק חשמלי – קצר הוא מצב שהמוליכות ‪ ,‬במסלול החשמלי קטנה או אפסית ביחס‬ ‫למתוכנן ‪ .‬כהמשך למצב זה ‪ ,‬יש זרם ‪ ,‬שהמוליכים אינם מתוכננים להובילו ומתפתח חום ‪,‬‬ ‫וכל נזק אפשרי ‪ .‬אם יש הגנה ‪ ,‬כל שהיא‪ ,‬היא מנתקת את המוליך או מפסיקה את המתח‪,‬‬ ‫בדרך כלל ‪ ,‬על ידי נתיכים )‪ , (Fuses‬הנזק שגורם הקצר יכול להוביל להתכת מוליך ‪ ,‬ולכן‬ ‫ל נתק ‪ .‬בדרך כלל הקצר מספיק לגרום לנזקים בפרק זמן קצר מאד ‪ ,‬ולכן אסור לחדש את‬ ‫ההולכה ‪ ,‬בלי לתקן את הסיבה ל קצר ‪ ,‬וחייבים לחדש את ההגנה מקצר‪ ,‬רק על ידי רכיבים‬ ‫שמהירות תגובתם מתאימה לתכנון ‪ .‬בקצור‪ -‬אסור להחליף נתיך בסתם חוט מתכת כל‬ ‫שהוא‪.‬‬ ‫התנגדות חשמלית – היא המידה שחומר מתנגד למעבר זרם חשמלי ‪ .‬נגד ‪ R‬הוא רכיב‬ ‫אשר התנגדותו ופיזור החום ממנו תוכננו מראש‪ ,‬על ידי בחירת החומרים הצורה והמידות ‪.‬‬ ‫קבול – קבול חשמלי הוא מצב של הצטברות מטענים בין שני מוליכים ‪ ,‬שיש ביניהם חומר‬ ‫מבודד או ריקנות ‪ .‬בלשון אחרת‪ ,‬אין זרימה ישיר ה בינהם ‪ ,‬אלא הצטברות של של מטענים‬ ‫מנוגדים עד לשיוויון מספרי‪ .‬קבל ‪ C‬הוא רכיב שקבולו המירבי תוכנן מראש ‪ .‬תהליך‬ ‫ההצטברות של המטענים או הפריקה שלהם מכונה זרם טעינה וזרם פריקה‪.‬‬ ‫קבל טעון מהווה נתק בקו בו זורם זרם בכיוון אחד ‪ .‬בין שני המוליכים יש שדה חשמלי ‪E‬‬ ‫שערכו תלוי במתח ‪ U a-b‬בינהם ‪ .‬ערך הקיבול ‪ C‬הוא היחס בין המטען ‪ Q‬למתח ‪. U‬‬ ‫השראות – בכל עת‪ ,‬שזרם חשמלי‪ ,‬עובר במוליך ‪ ,‬נוצר סביבו שדה מגנטי ‪ .‬באופן הפוך‬ ‫כאשר מוליך עובר בשדה מגנטי נוצר בו זרם ‪ .‬להשפעה ההדדית בן מוליכים ושדה מגנטי ‪,‬‬ ‫קוראים השראה מגנטית ‪ .‬כדי לקבל את התו פעה בגדלים שימושיים מלפפים את‬ ‫המוליכים לצורות שונות המכונות סלילים ‪ .‬המרווח בין הליפופים הוא אחד הגורמים ‪,‬‬ ‫שמאפשר לתכנן סליל ל השראות ‪ , L‬שרצויה לשמוש מסויים ‪ .‬גורמים נוספים ‪ ,‬שמשפיעים‬ ‫על ההשראות ‪ ,‬הם עצמת הזרם ‪ ,‬קוטר הליפוף ‪ ,‬החומר שמעליו מלפפים ועוד‪.‬‬ ‫זרם ישר ‪ – D.C.‬זה זרם של מטענים חשמליים ‪ ,‬הנעים באותו כוון ובאותו קצב ‪ .‬המסלול‬ ‫של זרם חשמלי עובר דרך מוליכים וצרכנים שונים כדי לבצע עבודה ‪ .‬בכל מקרה‪ ,‬כדי‬ ‫שתהיה זרימה ‪ ,‬המסלול מתחיל ממקור ביציאה של הפוטנציאל הגבוה וחוזר לנקודה של‬ ‫הפוטנציאל הנמוך‪ ,‬ולכן מכנים זאת " מעגל חשמלי "‪ .‬הזרם הישר‪ -Direct Current -‬הוא‬ ‫תוצאה של מתח ישר – שאינו משתנה בקוטביותו ורמתו ‪ .‬לדוגמה כל המצברים והסוללות‪.‬‬ ‫זרם חלופין ‪ Alternating Current – A.C.‬הוא זרם אשר משנה את עצמתו וכיוונו ביחס‬ ‫לזמן ‪ .‬המקור לזרם כזה הוא מקור מתח חילופין ‪ .‬השינויים בעצמה ובכוון ‪ ,‬בדר ך כלל ‪,‬‬ ‫מתרחשים במחזוריות מתוכננת מראש‪ .‬ישנם סוגים רבים ומשונים של זרמי חילופין ‪ ,‬והם‬ ‫מקבלים כינויים שונים ‪ ,‬אך כדרך כלל ‪ ,‬מתכוונים לזרם ‪ ,‬שהשינויים בו הם במחזוריות‬ ‫קבועה ‪ ,‬ומכונה תדירות הזרם או המתח ‪ .‬המקור לזרם חילופין נקרא " מחולל " זרם חילופין‬ ‫אך זה יכול לקבל ש מות שונים כמו ‪Oscillator,Alternator:‬‬ ‫‪ Generator‬ועוד‪.‬‬ ‫תגובת הרכיבים ‪ :‬נגד קבל וסליל ‪ – .‬כאשר נגד מחובר בין שתי נקודות מתח ‪ ,‬אומרים‬ ‫שתפקידו " להפיל מתח " ‪ ,‬או כשהוא מוכנס למסלול זרם אומרים שתפקידו ל " הגביל זרם "‪.‬‬ ‫וככלל ‪ ,‬זה יהיה נכון‪ ,‬הן בזרם ישר והן בזרם חילופין ‪ .‬תגובת הנגד היא התנגדות ‪.‬‬ ‫תגובות הקבל והסליל הן שונות‪ .‬קבל בזרם ישר ‪ ,‬לאחר שמפסיק זרם הטעינה הופך‬ ‫לנתק ‪ .‬סליל בזרם ישר לאחר שנבנה סביבו השדה המגנטי יהפך לקצר או קרוב לקצר ‪.‬‬ ‫בשני המקרים ברגע החיבור או הניתוק מתקבל ניצוץ; עובדה זו מוזכרת כדי להזהיר‬ ‫מפעולות של ט יפול במתקנים חשמליים בסביבה של אדים או נוזלים דליקים ‪ .‬הניצוץ נוצר‬ ‫משום שברגע הניתוק או החיבור מרווח האויר בין המגעים קטן למידה ‪ ,‬שהוא אינו מבודד ‪,‬‬ ‫והוא נפרץ על ידי המטען של הקבל או השדה המגנטי של הסליל ‪ .‬הן בקבל והן בסליל יש‬ ‫הולכה של זרם חילופין ‪ ,‬ולפי המבנה ש להם הם " מתנגדים " באופן מסויים לזרם החילופין ‪,‬‬ ‫והם אינם קצר או נתק מוחלטים ‪ .‬כדי לאפיין את תגובתם לזרם משתמשים ביחס לקבל‬ ‫ב " הגיב קיבולי " וביחס לסליל " הגיב השראתי "‪.‬‬ ‫להרכב של הגיבים אלה עם נגדים קוראים " עכבת " ‪ . Impedance‬במציאות בכל אחד‬ ‫משלושת הרכיבים יש מידה מס ויימת מהשניים האחרים ‪ .‬באופן מעשי‪ ,‬כשרכיב מתוכנן‬ ‫לישום ‪ ,‬כל שהוא ‪ ,‬הערכים של השניים האחרים זניחים ‪ .‬אך כל הכתוב לעיל בא להזהיר את‬ ‫מי שאינו מוסמך ‪ ,‬מהחלפת רכיבים בלי להכיר את הטכנולוגיה שלהם‪ .‬חוץ מהמידות‬ ‫והחומרים מהם מורכבים הקבלים והסלילים הגורם המשפיע על תגובת ם הוא תדירות זרם‬ ‫החילופין ‪ ,‬שתוגדר בהמשך‪.‬‬ ‫המקרה הנפוץ ביותר ‪ ,‬בו יש עניי ן בעכבת ‪ ,‬הוא כאשר נדרשים לחבר אנטנה למכשיר‬ ‫קליטה או שידור ‪ .‬לזוג מוליכים שמוביל אנרגיה חשמלית קוראים " קו‪ -‬תמסורת"‪ .‬לכל קו‬ ‫תמסורת והמכשירים שמחוברים אליו יש עכבת כניסה ויציאה‪ .‬על מנת להעבי ר את‬ ‫האנרגיה ביעילות המירבית עכבת היציאה צריכה להיות זהה לעכבת הכניסה בחיבור‬ ‫בינהם ‪.‬‬ ‫לדוגמה אם עכבת הכניסה לאנטנה של מכשיר קשר ימי היא ‪ 51‬אוהם ‪ ,‬אז גם הכבל‬ ‫שמחבר מהאנטנה למכשיר צריך להיות עם כניסה ויציאה של ‪ 51‬אוהם וגם חיבור הכניסה‬ ‫למכשיר צריך להיות ‪ 51‬א והם ‪.‬‬ ‫ראוי לזכור שאי אפשר למדוד את העכבת עם מכשיר המכונה אוהם‪ -‬מטר ‪ ,‬המדידה דורשת‬ ‫ידע מחוץ למסגרת של חוברת זו‪ .‬עם זאת ‪ ,‬חשוב לזכור ‪ ,‬שנתן לקרא את ערך העכבת‬ ‫האופיינית של כל אנטנה ‪ ,‬כבל או מכשיר‪ ,‬על גוף המתקן ‪ ,‬בקטלוג או בספרות הטכנית‬ ‫שלו ‪ ,‬וכך לרכוש רכיבים שיתאימו אחד לשני ‪ .‬ישנם גם רכיבים שמתאמים בין עכבות‬ ‫שונות ‪ ,‬לדוגמה‪ ,‬חלק מהאנטנות ‪ ,‬לקליטת ערוצי הטלויזיה ‪ ,‬הן בעלות עכבת של ‪ 311‬אוהם‬ ‫וכך גם קו התמסורת השטוח שמחובר אליהן; אך בקצהו ישנו רכיב תאום‬ ‫ל‪ 75 -‬אוהם של הכניסה למקלט הטלויזיה ‪.‬‬ ‫קבול של תא או סוללת תאים חשמליים – תא חשמלי הוא מתקן ‪ ,‬שאגורה בו אנרגיה‬ ‫חשמלית‪ ,‬ובסגירת מעגל דרך צרכן ‪ ,‬נתן להפיק ממנו זרם ישר לזמן קצוב ‪ .‬את התאים נתן‬ ‫לחבר כך שיתקבל מתח גבוה ‪ ,‬או זרם גדול יותר ‪ ,‬מאשר מתא בודד ‪ .‬את החיבור אנו‬ ‫מכנים " סוללה "‪ .‬אם התאים הם מסוג‪ ,‬שנתן להטעינו לאחר שנוצל ‪ ,‬אנו מכנים אותם בשם‬ ‫" מצברים " או " סוללות נטענות "‪.‬‬ ‫לאחר שתא חשמלי‪ ,‬או סוללה של תאים מחוברים ‪ ,‬הוטענו ‪ ,‬הצטברה בם אנרגיה ‪,‬‬ ‫בצורה של מטענים ‪ ,‬אשר נתן להזרימה אל הצרכנים הרצויים ‪ .‬משך הזמן שתא או סוללה ‪,‬‬ ‫יכולים לספק זרם נקוב ‪ ,‬במתח קבוע ‪ ,‬מכונה קבול המצבר‪ .‬כאשר מתכננים‪,‬‬ ‫או רוכשים סוללה ‪ ,‬למכשור כל שהוא ‪ ,‬לפני כל נתון אחר נרצה לדעת ‪ ,‬שמתח הסוללה‬ ‫מתאים למתח ההפעלה של המכשור‪ ,‬והיא מסוגלת לספק את כלל הזרם הדרוש למספר‬ ‫שעות ההפעלה‪.‬‬ ‫מתח הסוללה נקבע לפי מספר התאים שמחוברים בטור כלומר קוטב (‪ )+‬של‬ ‫תא אחד לקוטב (‪ ) -‬של התא הבא אחריו ‪ .‬לדוגמה אם רוצים להרכיב סוללה‬ ‫שתספק ‪ 12‬וולט‪ ,‬מתאים של ‪ 2‬וולט ‪ ,‬דרושים ‪ 6‬תאים ‪ . 12 = 2 X 6‬כל תא‪ ,‬לפי‬ ‫כמות החומר שבו ( מידותיו ) עשוי לספק זרם מסויים לזמן מסויים; זה כאמור‬ ‫מכונה " קבול התא " והוא מצויין ביחידות המכונות " אמפר‪ -‬שעות " ‪ .‬בסוללה‪,‬‬ ‫שמורכבת ממספר תאים בטור ה‪ " -‬אמפר‪ -‬שעות " של כל הסוללה דומה לזה של‬ ‫כל תא בודד ‪.‬‬ ‫כדי להגדיל את ה‪ " -‬אמפר‪ -‬שעות " צריך לחבר תאים או סוללות במקביל ‪.‬‬ ‫לדוגמה‪ :‬אם כל אורות הדרך של ספינה מוזנים מסוללה של ‪12 V‬‬ ‫והם צורכים זרם של ‪ , 6 A‬האורות אמורים לדלוק בממוצע ‪ 8‬שעות ‪ .‬הקבול‬ ‫הדרוש הוא של ‪ . 48 Ah = 8 h X 6 A‬מבחינה חישובית התוצאה נכונה ‪ ,‬אך‬ ‫מבחינה של אמינות ‪ ,‬לא נרצה להגיע למצב שהמצבר התפרק מכל האנרגיה‬ ‫שהייתה אגורה בו ‪ ,‬מצברים מסוגים מסויימים עלולים להכנס למצב בלתי הפיך‪,‬‬ ‫כך שלא יהיה נתן להטעין אותם ‪ ,‬וכן רצוי שתשאר עתודת אנרגיה לתוספת‬ ‫זמן הפעלה ‪ .‬על ס מך נסיון מצטבר‪ ,‬מקובל להפעיל סוללה ב‪ -‬שליש או חצי‬ ‫מ " אמפר‪ -‬שעות " הנקוב על ידי היצרן‪ .‬בהתיחס לדוגמה ‪ ,‬שלעיל ‪ ,‬נזדקק למצבר‬ ‫של כ‪ . 81 Ah -‬ישנם עוד הרבה פרטים שדרושים כדי לבחור מצבר מתאים ‪ ,‬אך‬ ‫במסגרת פרק זה יצויין ‪ ,‬שלצרכי התנעת מנועים דרושים מצברים ‪ ,‬שמסוגלים‬ ‫לתת כמה מאות אמפרים למספר שניות‪ ,‬לדוגמה ‪ 311‬אמפר ל‪ 11 -‬שניות‪.‬‬ ‫‪ 11‬שניות הן בקרוב ‪ 1.113‬שעות ומזה מתבקש מצבר של כ‪311 A . 1.8 Ah -‬‬ ‫יפרקו במהירות מצבר כזה ‪ ,‬ולכן בוחרים מצבר בקבול גדול פי כמה עשרות ‪. Ah‬‬ ‫המצברים לצורכי התנעה בלבד בנויים כך שתגובתם תהיה מהירה ‪ ,‬לשימושים‬ ‫אחרים המצברים בנויים בשוני מבני ומכונים ‪ , Deep Cycle‬כלומר מחזור ארוך‬ ‫של צריכה וטעינה‪.‬‬ ‫עבודה חשמלית – " קילו‪ -‬ווט ‪ -‬שעה " ‪ -:‬עבודה חשמלית מבוצעת כאשר מתח גורם לתנועה‬ ‫או הצטברות של מטען חשמלי ‪ .‬כמות המטען החשמלי הוא המכפלה של זרם בזמן הזרימה‬ ‫‪ , Q = I x t‬והמתח מסומן ב‪ U -‬כך העבודה ביחידות ‪ Joul‬היא ‪. U x I x t = W‬‬ ‫היצרנים של מכשור חשמלי מחוייבים לציין על המכשירים את צריכת הזרם שלהם‪,‬‬ ‫וההספק‪ .‬זאת כדי שהצרכנים יוכלו לחשב עלות והפעלה תקינה ‪.‬‬ ‫ההספק החשמלי – הוא העבודה החשמלית ביחידת זמן ‪ ,‬ונמדד ביחידות ווט ‪.‬‬ ‫בשימוש הנפוץ משתמשים במאות ואלפי ווטים ולכן משתמשים ב‪ -‬קילו‪ -‬ווטים ‪,‬‬ ‫והזמן נמדד בשעות‪ .‬כדי להבין את הסימונים ‪ ,‬ומשמעות הערכים הנקובים ‪ ,‬נפתח‬ ‫את רצף הנוסחאות המגדירות ‪ -:‬העבודה ‪U x I x t = W‬‬ ‫‪U I t‬‬ ‫‪W‬‬ ‫‪ U I  P‬‬ ‫ההספק הוא ‪ P‬‬ ‫‪t‬‬ ‫‪t‬‬ ‫העבודה ‪ W‬יכולה להיות ‪ P x t = W‬מתצוגה זו גזורה היחידה לחישוב עלות החשמל‪,‬‬ ‫שמכונה קילו‪ -‬ווט שעה ‪ , KWh‬כלומר כמה אלפי‪ -‬ווטים צרכנו במשך כמה שעות ‪ .‬זו גם‬ ‫היחידה שמציג מונה החשמל הביתי‪ .‬לחישוב העלות מכפילים את המחיר הנקוב‬ ‫ל‪ 1KWh -‬במספר שמראה המונה‪.‬‬ ‫ומכאן‬ ‫תדירות ‪ – f‬כאשר תופעה פיסיקלית מתרחשת במחזוריות‪ ,‬כלומר ערך מסויים מופיע‬ ‫במרווחי זמן קבועים ‪ ,‬אשר הם זמן המחזור ‪ , T‬אומרים שלתופעה יש תדירות ‪ .‬מספר‬ ‫המחזורים ביחידת זמן הוא התדירות ‪ .‬בעוד שמספר המחזורים יכול לקבל ערכים שונים‬ ‫יחידת הזמן הנפוצה היא השניה ומקובל לסמן " מחזו רים לשניה " ‪Cycles Per Seconds‬‬ ‫ומסמנים ‪ . C/S‬לדוגמה המתח שמספקת חברת החשמל הוא מתח חילופין‬ ‫בתדירות של ‪ . 51 C/S‬כלומר הערכים הרגעיים של המתח המשתנה מופיעים ‪ 51‬פעמים‬ ‫בשניה אחת ‪ .‬במקום ‪ C/S‬מקובל ‪ ,‬בתחום התקשורת ‪ ,‬כנוי היחידות של התדירות ב " הרץ "‪.‬‬ ‫לדוגמה גלי הרדיו הם סוג של מתח חילופין ‪ ,‬ואם משדר מסויים מקרין מתח מתחלף‬ ‫‪ 518111‬מחזורים בשניה מסמנים ‪ . 518 x 10 3 Hertz = 518KHZ‬בדווח על תנאי מזג אויר‬ ‫וים ‪ ,‬מקובל לדווח את תדירות הגלים ‪ ,‬על ידי מדידת מספר השניות ‪ ,‬שחולף מהרגע ‪,‬‬ ‫שרואים פסגת גל עד שמופיעה פסגה אחרת באותו מקום‪ .‬התדירות ת היה‬ ‫אחד חלקי זמן המחזור המדוד ‪.‬‬ ‫ספקטרום ופס‪ -‬תדרים – היות ויש צורות שונות של אנרגיה שמופיעות בצורה מחזורית‪,‬‬ ‫חלקו את המאפיינים והשימושים לסולמות שיש להם מכנה משותף ‪ .‬הסולם מכונה‬ ‫ספקטרום ‪ .‬כל ספקטרום נתן לתת‪ -‬חלוקות לפי סוג הענין‪ .‬מהידועים יותר הוא ספקטרום‬ ‫האור הנראה – צבעי הקשת; וספקטרום הגלים האלקטרומגנטיים ( הרדיו )‪.‬‬ ‫תת‪ -‬חלוקה של ספקטרום מכונה פס‪ -‬תדרים ‪ ,‬שאף הוא עשוי להיות מחולק‬ ‫לתת‪ -‬פסים או פסי משנה ‪ .‬היות ולצרכי תקשורת‪ ,‬בדרך כלל ‪ ,‬השדורים תופשים‬ ‫יותר מתדר בודד על סולם התדרים ‪ ,‬מקוב ל השימוש בבטוי " רוחב הפס " כלומר‬ ‫ההפרש בין התדר הגבוה ביותר לנמוך ביותר הדרוש כדי להעביר מידע ‪.‬‬ ‫‪. F2-f1= Δf = Band Width=BW‬‬ ‫ערוץ ‪ /‬אפיק ‪ – CHANNEL‬היות ותדרים גבוהים נכתבים במספר של מעל ל‪ 6 -‬ספרות‪,‬‬ ‫וכן ישנם שימושים שבהם משתמשים ביותר מתדר אחד בו זמנית ‪ ,‬מקובל בתחום‬ ‫התקשורת להשתמש בכינו י מקוצר עד ‪ 3‬ספרות‪ .‬לדוגמה בתקשורת‬ ‫הימית התדר ‪ 156.525MHz‬משמש לתקשורת ספרתית ומכונה ערוץ ‪.71‬‬ ‫ים של זויות ‪ -‬אגרון של מושגים הקשורים בזוויות ‪-:‬‬ ‫‪ – ANGLE‬זווי ת = זווי ת היא ה צורה ‪ ,‬במישור כל שהוא ‪ ,‬שנוצר ת בין שני קווים ישרים‬ ‫החותכים זה את זה‪ .‬את היחס בין הישרים מתארים על ידי חלוקת מעגל שמרכזו בנקודת‬ ‫החיתוך ‪ ,‬נקודת החיתוך נקראת " קודקוד הזוית "‪ .‬מעתה‪ ,‬כיוון = זווי ת במעגל ( המחולק‬ ‫בחלוקה רציפה ל‪ 361 1 -‬קרא בהמשך)‪.‬‬ ‫להגדרת ערך הזוית‪ ,‬מחלקים את המעגל לחלוקות שונות ‪ ,‬לפי השימוש‪ ,‬בימאות‬ ‫העכשוית‪ ,‬מקובלת החלוקה ל‪ , 361 1 -‬החלוקה למעלות נקראת גם " חלוקה רציפה " ‪ ,‬ישנן‬ ‫חלוקות אחרות ( חלוקה " רבעית " בנווט אסטרונומי ‪ ,‬וחלוקה " נקודית " ‪ -‬ראה פרק מצפנים‬ ‫ב " עזרי נווט וקשר ")‪ .‬כשהישרים אינם נחתכים ‪ ,‬הם חופפים בכל נקודותיהם או מקבילים ‪,‬‬ ‫ובחלוקה ל‪ 361 1 -‬הם במצב ‪ ,‬שערך הזוית ‪ , 1 1‬או ‪. 361 1‬‬ ‫כל שני ישרים ‪ ,‬שמשורטטים במישור ‪ ,‬מקיימים מצב שנתן להופכו לערך זוית‪ .‬קו היחוס‬ ‫הוא אחד משני הקוים שיוצרים את הזוית אך הוא קו ‪ -‬הראשית ‪ ,‬שממנו מתחילים את‬ ‫המדידה כלומר ‪ ,1 1‬נתן להעתיק כל קו כך שתהיה לו נקודה ( קודקוד הזוית ) משותפת עם‬ ‫קו היחוס‪ .‬הבטוי ל " העתיק קו " או " להריץ כיוון " אומר להסיע קו במישור מבלי שישנה את‬ ‫מצבו ביחס ל " קו היחוס "‪.‬‬ ‫שני קוים אשר אינם חופפים ואין להם כל נקודה משותפת נקראים קווים " מקבילים "‬ ‫והזוית בינהם היא ‪ . 1 1‬כאשר " מעתיקים קווים " במפה ‪ /‬במישור מבצעים פעולה של " הסעה‬ ‫מקבילה " או " הסעה ‪ /‬העתקה במקביל "‪.‬‬ ‫הצורך להסיע במקביל נובע מכך ש‪ -‬א ) מישור העבודה ( המפה הימית) מוגבל בגודלו ‪ ,‬אם‬ ‫היה מעשי לראות מישור גדול בלי גבול ‪ ,‬היינו רואים את נקודות החיתוך ( קודקוד הזווית )‬ ‫של כל שנ י קווים מבלי להעתיק אותם ‪ ,‬ו‪ -‬ב ) יש צורך להעתיק ערכים של זויות שונות מתוך‬ ‫מעגל הנמצא במקום שונה מאזור השרטוט ‪.‬‬ ‫לבד מנווט ופתירת מצבים בנתוב ופנוי דרך ‪ ,‬נעשה שמוש בזויות ‪ ,‬ובחוקים של הנדסת‬ ‫המישור‪ ,‬גם במפרשנות ‪ ,‬פעולת לוח ההגה ‪ ,‬רתוק ושנוע מטענים ‪ .‬נזכור גם שקוי הר שת‬ ‫הגיאוגרפית ‪ ,‬שמשמשת לציון אתרים על כדור הארץ ובמפות הימיות ‪ ,‬מקבלים את שמם‬ ‫מערכי זוית ‪ 81 1 .‬לציון ‪ 81‬קוי רוחב צפונה לקו המשווה‪ ,‬ו‪ 81 1 -‬לציון ‪ 81‬קוי רוחב דרומה‬ ‫לקו המשווה; וכן ‪ 181 1‬לציון ‪ 181‬קווי אורך מזרחה לקו ‪ 1 1‬העובר ב‪, Greenwich -‬‬ ‫ו‪ 181 1 -‬לציון ‪ 181‬קוי אור ך מערבה לקו ‪ 11‬העובר ב‪ ( Greenwich -‬עיירה ליד לונדון )‪.‬‬ ‫‪ POSITION LINE =PL‬או ‪ – LOP Line Of Position‬קו אתר‪ -‬קו כל שהוא שעל‬ ‫אחת מנקודותיו עשוי להיות כלי השיט ‪ .‬הקו משורטט במפה על סמך חישוב או‬ ‫מדידה במכשיר נווט כל שהוא‪.‬‬ ‫קו האתר מופק על ידי קריאת זויות ו ‪ /‬או מדידת טווחים ‪ .‬הקו יכול להיות ישר ‪ ,‬עקום‬ ‫מעגל או קשת אך חייב להכיל איפיון משותף לכל נקודותיו ‪ .‬יאמר כבר כאן ‪ ,‬שמקומו‬ ‫המדוייק של כלי שיט מתקבל מהחיתוך של ( לפחות ) שני קוי אתר כל שהם‪ ,‬והוא‬ ‫מכונה ‪. FIX‬‬ ‫‪ = TRUE NORTH‬צפון אמיתי ‪ /‬גיאוגרפי ‪ -‬הכיוון אליו מצביע הקו המהווה את ציר הסיבוב‬ ‫של כדור הארץ ‪ ,‬כאשר הנקודה ממנה הוא יוצא מ ה כדור ( בחצי בו נמצאות יבשות אירופה‬ ‫ואמריקה ) מוסכמת כקוטב צפוני ‪ ,‬וממנה מתחילה ספירת החלוקה של מעגל האופק ‪ ,1 1‬כל‬ ‫זוית הגדולה מ‪ , 1 1 -‬תתואר על ידי חיתוך של שני קוים ‪ ,‬אחד ‪ 1 1‬והשני עובר דרך נקודה‬ ‫נבחרת במפה ( מרכז מעגל האופק ‪ /‬קודקוד הזוית בו נמצא הצופה )‪.‬‬ ‫‪ -TN‬הצפון האמיתי ‪ 111 1‬או ‪ , 361 1‬שהיא נקודת הראשית בחלוקת מעגל האופק ‪.‬‬ ‫‪ = MAGNETIC NORTH‬צפון מגנטי – זה הכוון איתו יתלכד‪ ,‬ואליו יצביע‪ ,‬הסימון של ‪1 1‬‬ ‫או ‪ 361 1‬או ‪ NORTH‬ב לוח חלוקת מעגל האופק ‪ ,‬של מצפן מגנטי ‪ .‬זאת בתנאי שאין‬ ‫השפעה של גופים העשויים ממתכות שהן בעלות תכונה מגנטית ‪ .‬ל זוית שבין הצפון‬ ‫האמיתי והצפון המגנטי קוראים שגיאת הווראציה‪ . VARIATION -‬ההבדל נובע מכך‬ ‫שכדור הארץ הוא בעל תכונות מגנטיות שמשתנות הן מאזור לאזור והן עם חלוף הזמן‪.‬‬ ‫כשה‪ , 1 1 = VARIATION -‬הצפון המגנטי זהה לצפון האמיתי‪.‬‬ ‫‪ = COMPASS NORTH‬צפון המצפן ‪ -‬זה הכוון איתו יתלכד‪ ,‬ואליו יצביע‪ ,‬הסימון של ‪1 1‬‬ ‫או ‪ 361 1‬או ‪ NORTH‬ב לוח חלוקת מעגל האופק ‪ ,‬של מצפן מגנטי ‪ ,‬אך גם של כל מצפן‬ ‫אחר ‪ ,‬אשר שגיאתו אינה נובעת משדות מגנטיים ‪ .‬במצפנים מגנטיים כאשר בנוסף ל‪-‬‬ ‫‪ VARIATION‬ישנה גם השפעה מגנטית של גופים מתכתיים במבנה כלי השייט ומטענו ‪.‬‬ ‫לזוית שבין צפון המצפן ‪ CN‬לצפון המגנטי ‪ MN‬קוראים דביאציה‪. DEVIATION -‬‬ ‫כשה‪ 1 1 = DEVIATION -‬צפון ה מצפן המגנטי זהה לצפון המגנטי ‪.‬‬ ‫‪ = COMPASS ERROR‬שגיאת המצפן – במצפן מגנטי = הסכום האלגברי של זוית‬ ‫הווראציה וזוית הדביאציה ‪ .‬את זוית הוראציה מפיקים מסימון או רישום באזור השייט‬ ‫במפה הימית‪ ,‬את זוית הדביאציה מפיקים מטבלה או גרף ‪ ,‬שמוכן לכל כלי שייט שהחוק‬ ‫מחייבו לכך ‪ .‬הסכום הוא " חבור אלגברי " משום שפעמים נחסר ופעמים נסכם את שתי‬ ‫הזויות ‪ .‬כאשר מגמתם זהה מערבה או מזרחה מהצפון נסכם את ערכן ‪ ,‬וכאשר מגמתן‬ ‫שונה ‪ ,‬האחת מערבה והשניה מזרחה ‪ .‬נחסר את ערך הקטנה מהגדולה ומגמת התוצאה‬ ‫תקבל את כינוי הגדולה מבין השתיים ‪ .‬נתן להפיק את שגיאת מצפן כל שהוא ( גם לא‬ ‫מגנטי ) בכמה שיטות ‪ -:‬ישירות על ידי תצפי ת אל אתרים שמזוהים בו זמנית הן בעין והן‬ ‫במפה ‪ ,‬או בתצפית לגורמי שמים ‪ .‬באופן כללי על ידי פעולה של השוואת קריאת המצפן‬ ‫לתכווינים אמיתיים מהמפה הימית ( או מחושבים ומתוקנים ) ראה ‪. TRANSIT-BEARING‬‬ ‫‪ -STEERING COMPASS‬מצפן המותקן לשמושו של ההגאי בהגה יד או ל " נתב‬ ‫אוטומטי "‪.‬‬ ‫‪ -STANDARD COMPASS‬המצפן התקני של כלי השייט ‪ ,‬זה‬ ‫ששגיאתו נתנת לחשוב ‪ ,‬או ידועה בכל עת ( ביחס אליו בוצעה טבלת‬ ‫הדוויאציה )‪.‬‬ ‫בתמונה מצפן מגנטי ‪ ,‬בתוך מיכל גלילי ממתכת לא מגנטית ‪ .‬המיכל מותקן על‬ ‫גליל עץ ‪ ,‬אשר בהמשכ ו מחובר פריסקופ דרך הגג של חדר ההגה ( החלק החשוך )‪.‬‬ ‫שני כדורי ברזל נתנים להזזה ‪ ,‬ובתוספת מוטות ברזל הנמצאים בתוך גליל ‪ ,‬בצד‬ ‫המוסתר ‪ ,‬מאפשרים הפיכת סביבת המצפן ‪ ,‬וכלל כלי השייט ‪ ,‬לנטולת השפעה‬ ‫מחלקי המתכת של מבנה כלי השייט ‪ .‬המצפן מוגן מהשפעות מזג אויר אך נתן‬ ‫לפתוח צוהר ( העגול העליון ) ולהדליק תאורה פ נ ימית ‪ ,‬ועוד ישנו צנור אויר ‪ ,‬שפתחו‬ ‫בגליל העליון בצד ימין כולל צפצפה ‪ ,‬זה כדי לאפשר דו שיח עם ההגאי שלמטה ‪.‬‬ ‫הדבור דרך צינור אויר נעשה כדרישה בטיחותית של אי‪ -‬תלות בחשמל ‪ .‬במצפנים‬ ‫אלה נתן להסיר את הכסוי העליון ולהרכיב מד‪ -‬תכוויני ם לשתי מטרות ‪ :‬האחת‬ ‫לצורך הכנת גרף או טבלת דוויאציה ‪ ,‬והשניה לצורך בדיקה מעת לעת או השוואה‬ ‫עם מצפנים אחרים שאינם מתוקנים ‪.‬‬ ‫‪(Hand Bearing Compass) BEARING COMPASS‬‬ ‫ מצפן ( מטלטל בדרך כלל ) אשר בעזרתו נתן לקבל תכווינים מסביב למעגל האופק של‬‫כלי השייט ‪.‬‬ ‫‪ -VAR‬אחד המרכיבים בשגיאה של המצפנים המגנטיים ‪ ,‬הזוית שבין הצפון המגנטי ‪,‬‬ ‫שבמקום נתון על כדור הארץ ‪ ,‬והצפון האמיתי‪.‬‬ ‫‪ - DEV‬אחד המרכיבים בשגיאה של מצפנים המגנטיים ‪ ,‬הזוית שבין צפון מצפן‪ -‬מגנטי‬ ‫והצפון המגנטי במקום נתון על כדור הארץ ובכוון נתון של כלי השיט ‪.‬‬ ‫‪ - MN‬הצפון שמורה מצפן מגנטי לאחר תיקון ה‪.DEV -‬‬ ‫‪ - CN‬צפון מצפן ‪ ( ,‬לא דוקא מצפן מגנטי ) ‪ ( ,‬ללא תקון שגיאות )‪.‬‬ ‫‪ -TC=True Course‬נתיב אמיתי ( גיאוגרפי ) משורטט ‪ ,‬מופק או נתן בין שני אתרים‬ ‫במפה ‪ ,‬הוא שוק הזוית עליה אמור לנוע כלי שיט אל יעדו ‪ .‬לידו מסמנים את ערך הזוית‬ ‫שהוא יוצר עם הצפון האמיתי ‪. TN‬‬ ‫במפת מרקטור‬ ‫קווי האורך‬ ‫מקבילים לקו ‪TN‬‬ ‫‪ - MC‬קורס ( זוית במעלות ) שבין ‪ MN‬וקו הנתיב המתוכנן של כלי השיט‪.‬‬ ‫‪ - CC‬קורס ( זוית במעלות ) שבין ‪ CN‬וקו הנתיב המתוכנן של כלי השיט‪.‬‬ ‫‪ Course To Steer – CTS‬התקון ב‪ TC -‬שיש לבצע כדי להגיע ליעד‪ ,‬ולבטל בכך‬ ‫את השפעת ה‪ LEEWAY -‬ו ‪ /‬או ה‪ ( CURRENT -‬ראה הגדרות בהמשך)‪ .‬תקון זה יש לבצע‬ ‫לפני תקון מצפן להגאי ‪ .‬כשכתוב " קורס להגוי " ראוי לברר את הכוונה‪ :‬האם זה תרגום של‬ ‫‪ CTS‬או הקורס לאחר תקון שגיאת המצפן = קורס להגאי ‪...‬‬ ‫‪ – HEADING‬כוון חרטום ‪ ,‬כלי השיט ‪ ,‬ברגע נתון ‪ ,‬לא בהכרח קורס ‪ ,‬גם בעגינה או‬ ‫במצב ללא שליטה‪ ,‬ובחציה של נתיב להפרדת תעבורה ‪ .‬ה‪ HEADING -‬יכו ל להיות אמיתי ‪,‬‬ ‫מגנטי או מצפני ‪ .‬ה‪ Compass Heading -‬הוא הנתון ( נקודת הראשית) לבנית טבלת‬ ‫הדוויאציה של המצפן המגנטי ( התקני ) של כלי השיט‪.‬‬ ‫)‪ - TRACK (TRACK ANGLE‬הנתיב שבו נעה הספינה במים ‪ ,‬ואינו ‪ ,‬בהכרח כיוון‬ ‫החרטום ( ה‪ , ) HEADING -‬למטרות מסוימות שימושי להבדיל בין ‪-:‬‬ ‫‪ , WATER TRACK ANGLE‬שמכונה גם ‪ WAKE COURSE‬לבין ‪-:‬‬ ‫‪ GROUND TRACK ANGLE‬שהוא הנתיב שהיה מצטייר על קרקעית הים אילו נגעה‬ ‫בה שדרת הספינה תוך כדי תנועתה ‪.‬‬ ‫זה מכונה גם ‪.CMG= COURSE MADE GOOD‬‬ ‫‪Course/Heading‬‬ ‫וגם ‪. COG=COURSE OVER GROUND‬‬ ‫‪LeeWay‬‬ ‫‪Wind‬‬ ‫‪Water Track‬‬ ‫‪Wake/Water Track‬‬ ‫‪ " – LEE WAY‬טרידה " ערך הזוית שבה סוטה הספינה מה‪ TC -‬עקב רוח‪ .‬הזוית נמדדת‬ ‫בכוון שממבוא הרוח ( מעל הרוח ) אל הכוון של יציאת הרוח ( מתחת לרוח)‪.‬‬ ‫הערות ביחס לערך של זוית הטרידה ‪-: ” LEEWAY " -‬‬ ‫א ‪ .‬הרכיב של הרוח‪ ,‬שמשפיע על מהירות כלי השיט‪ " ,‬כלול " בערך המהירות ‪ ,‬שמציג‬ ‫מד מהירות המודד את המהירות ביחס למים ‪.‬‬ ‫ב ‪ .‬קשה מאד למדוד בדיוק את זוית הטרידה לצורך צפי של אתר משוער ‪ , EP‬וזה לא‬ ‫בגלל חסר בטכנולוגיה ‪ ,‬אלא בעקר בגלל שהרוח אינה יציבה בכיוונה ועצמתה ביחס‬ ‫לזמן ‪ ,‬והשפעתה שונה אפילו על שני כלי שייט מאותו דגם ‪ .‬אחת הדרכים להעריך‬ ‫את ערך הזוית היא על ידי הפנית מצפן‪ -‬תכווינים אל ה " חריש במים "‪WAKE -‬‬ ‫שמסמנת הספינה מאחורי ירכתיה ‪ ,‬והפחתת הקריאה מהערך ההפוך של הקורס ‪.‬‬ ‫כלומר ‪-:‬‬ ‫‪0‬‬ ‫‪0‬‬ ‫‪. LeeWay = (Course-180 ) - Wake Bearing 0‬‬ ‫‪ RELATIVE BEARING – RB‬הזוית במעלות שבין קו החרטום כ‪ 111 1 -‬וגוף‬ ‫כל שהוא בתחום האופק ‪ .‬מובע גם במעלות ימינה כירוק ‪ ,‬ושמאלה כאדום ‪.‬‬ ‫‪ TRUE BEARING – TB‬הזוית בין ‪ TN‬לגוף ‪ ,‬כל שהוא‪ ,‬בתחום האופק‪.‬‬ ‫‪ MAGNETIC BEARING -MB‬הזוית בין ‪ MN‬לגוף ‪ ,‬כל שהוא ‪ ,‬בתחום האופק‪.‬‬ ‫‪ COMPASS BEARING – CB‬הזוית בין ‪ CN‬לגוף ‪ ,‬כל שהוא ‪ ,‬בתחום האופק‪.‬‬ ‫‪ – TRANSIT BEARING‬זה התכווין ‪ ,‬שנמדד אל שני עצמים הנמצאים על קו ישר אחד עם‬ ‫הצופה ( המודד )‪ .‬היות ועל קו ישר יש שתי אפשרויות ‪ ,‬הקו שמתחיל מהצופה ועד לעצם‬ ‫הקרוב אליו הוא זה שמכתיב את ערך הזוית ‪ .‬נדיר מאד לכלי שיט להימצ א על קו כזה עם‬ ‫שני מגדלורים; ולא אמין לקרא תכוין כזה בין שני מצופים משום שהם מרותקים עם‬ ‫שרשרות ארוכות המאפשרות לזרם להסיטם מאתרם הרשו ם ‪ .‬עם זאת תכווין זה המכונה‬ ‫" תכווין מעבר " נתן לשמוש ‪ ,‬באור יום בין שני אתרים קבועים ‪ ,‬שמזוהים הן בעין והן‬ ‫במפה ‪ .‬תכווין כזה נותן מייד את השגיאה הכללית של המצפן ‪ . CE‬כדי להגדיר את מגמת‬ ‫השגיאה זכור את הכלל‪ :‬אם ערך קריאת המצפן גדול מהערך המדוד במפה‪ ,‬מגמת‬ ‫השגיאה ה יא ‪ WEST‬או ‪ . Compass Best Error West‬או אם ערך קריאת המצפן קטן‬ ‫מהערך המדוד במפה המגמה היא ‪. Compass Least Error East -EAST‬‬ ‫‪ – ABEAM‬תכווין ‪ 81 1‬יחסי לקו חרטום‪ -‬ירכתיים של כלי השייט ברגע מסוים‪,‬‬ ‫ולא בהכרח ‪ 81 1‬לקורס כל שהוא‪.‬‬ ‫‪ -LEADING LIGHTS/LINE‬כוון של קו בין שני אתרים ‪ ,‬או אורות ‪ ,‬שמטרתו להנחות כלי‬ ‫שיט לנתוב במעבר צר ‪ .‬האור שנראה נמוך מבין השניים‪ ,‬הוא הקרוב יותר‪ ,‬ואליו צריך‬ ‫לפנות עם חרטום הספינה כאשר רוצים לתקן סטיה מנתיב ההנחיה‪.‬‬ ‫‪ – SECTOR LINES‬קווים המתארים שני כיוונים המגבילים את כלי השייט לנת וב‬ ‫בגזרה בטוחה כדי להמנע ממכשולים למיניהם ‪.‬‬ ‫‪ -AZIMUTH‬מושג זה ‪ ,‬אינו שמושי בנווט חופי‪ ,‬אך תובא כאן הגדרתו ‪ ,‬משום שיש‬ ‫ה משתמשים בו במקום " תכווין "‪ .‬ובכן האזימוט הוא תכווין מיוחד ‪ .‬זהוא תכווין המשורטט‬ ‫במפה ( או נתן בטבלאות ) ממקומו המקורב של כלי השיט ‪ ,‬וב‪90 0 -‬‬ ‫לקו‪ -‬אתר שהופק מתצפית לגוף שמימי‪ .‬ב " קו‪ -‬אתר " = ‪POSITION LINE‬‬ ‫מתכוונים לקטע של מעגל ‪ ,‬שעל אחת מנקודותיו נמצא הצופה ‪ /‬כלי השיט‪.‬‬ ‫ראה " נווט אסטרונומי "‪.‬‬ ‫‪ " = ASPECT ANGLE‬חזות " – בעברית מדוברת כשאומרים " האספקט של ‪ "...‬מתכונים‬ ‫ל‪ -‬איך נראה ענין מסוים בעינים של משהוא אחר מהאומר ‪ .‬כך גם בנושא הימי ‪ ,‬ה " חזות "‬ ‫היא הזוית בה נראה כלי שיט אחד על ידי כלי שיט אחר‪ .‬הגדרה זו שימושית בפתירת‬ ‫בעיות של תנועה יחסית ‪ ,‬בפרט במכ " מ ‪.‬‬ ‫‪ - ALTITUDE‬זוית אנכית ‪ /‬זוית גובה ‪ /‬רום– זוית זו נמדדת על ידי מכשיר סקסטנט‪ ,‬או‬ ‫בטכנולוגיה אחרת ‪ ,‬מעל האופק הנראה‪ ,‬א ו מעל אופק מלאכותי ‪ .‬מדידת גובה של עצם‬ ‫מעל אופק מציבה את המודד על קו שהוא חלק ממעגל סביב העצם‪ .‬האזימוט מה עצם‬ ‫יחתוך את המעגל באתר הספינה‪.‬‬ ‫‪ " – 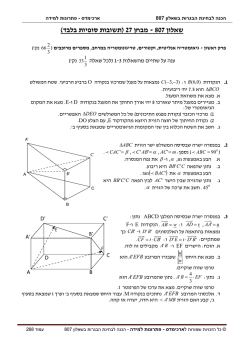Doubling on the bow‬הכפלת זוית על החרטום "‬ ‫על פי משפט הנדסת המישור ‪ ,‬אם בתחילת‬ ‫קטע ‪ , d‬נמדדת זוית ‪ a 0‬לנקודה שמזוהה הן‬ ‫בעין והן במפה ‪ ,‬ולאחר זמן ‪ ,‬מודדים זוית‬ ‫ש היא ‪ ; 2 X a 0‬אז אתר כלי השייט יהיה‬ ‫בקודקוד מש ולש שווה‪ -‬שוקיים ‪ ,‬כל שוק‬ ‫באורך ‪ , d‬כש‪ d -‬הוא גם המרחק ‪ ,‬שביו שתי‬ ‫המדידות‪.‬‬ ‫הזווית החיצונית ‪ ,2a‬במשולש שווה שוקים ‪,‬‬ ‫שווה לפעמיים הזוית הפנימית ‪. a‬‬ ‫‪ SET 0 +RATE /DRIFT knots =CURRENT‬מרכיבי זרם – כיוון במעלות ומהירות בקשרים ‪.‬‬ ‫הגדרה אחרונה זו ‪ ,‬של הזרם ‪ ,‬מובילה לצורך להגדיר ‪ ,‬כתוספת לזווית ‪ /‬כיוון גם את ערך‬ ‫המהירות של הזרם ‪ .‬אנו נדרשים להגדיר גודל שחייב לכלול בו זמנית ערך ‪ ,‬מתוך סולם‬ ‫נבחר ( מהירות בקשרים ) ‪ ,‬וכוון מתוך חלוקת מעגל (" שושנת רוחות ")‪ .‬כפי שהוסבר‬ ‫בהקדמה בסעיף ‪ .2‬מהירות ‪ , Velocity‬שייכת בתורת הפיזיקה ‪ ,‬לגדלים מסוג " וקטורים "‪.‬‬ ‫בטרם הסברת תכונות הוקטורים והכללים שלצורך פתרון בעיות של שיט מעשי ‪ ,‬תוגדרנה‬ ‫עוד מספר מהירויות‪.‬‬ ‫מהירות התנועה של כלי שיט‪SPD = Vessel Speed -‬‬ ‫מהירות כלי השיט כפי שנמדדה בין שני אתרים (‪ ) FIX‬ביחידות קשר ( מילים ימיים בשעה)‪.‬‬ ‫מהירות כזו תהייה "מהירותו האמיתית" של כלי השיט‪ ,‬בתנאי‪ ,‬שההגוי היה על קו ישר ללא‬ ‫גלים‪ ,‬רוח או זרם‪ .‬זו המהירות שהמשיט יתבסס עליה לצורך תכנון קטע או מסע שלם‪ .‬זו גם‬ ‫המהירות‪ ,‬שקל לבדוק אותה במרחק קצר‪ ,‬בתנאי ששטים הלוך וחזור מספר פעמים בין שני‬ ‫אתרים‪ ,‬שהמרחק בינהם ידוע‪.‬‬ ‫מדי‪ -‬המהירות הנפוצים מפיקים את " המהירות ביחס למים " – כלומר מהתנועה היחסית‬ ‫שבין המים לחיישן של מד המהירות ‪ ,‬ולכן בתוצאה המוצגת כלול ות‪ :‬השפעת רוח פנים או‬ ‫מ אחור ‪ ,‬חיכו ך הקוער ‪ ,‬שנויים במבנה מעל המים ‪ ,‬ופעולות מאטות של לוח ההגה ‪ .‬לא‬ ‫כלולה השפעת הזרם רכיב צד של הרוח )‪ (Leeway‬והעלייה וירידה מגלים ‪ " ,‬תנועה‬ ‫במפנים " ( בכוונים משתנים ) משום שאלה משנים את הכיוון ולכן את מה שמכונה‬ ‫" מהירות ההתקדמות ליעד "‪.‬‬ ‫ההתיחסות ל‪ -‬מהירות כלי שיט‬ ‫יכולה להבחן בשלושה הבטים ‪:‬‬ ‫א ‪ .‬בהבט של התכנון ההנדסי ‪ -‬מהירותו המרבית של כלי השיט ‪ ,‬שמאפשרים התכנון‬ ‫והבניה – של‪ -:‬אורך הקוער‪ / Hull- Speed /‬המדחף ‪ /‬סוג הקוער ‪ /‬המבנה שמעל המים ‪/‬‬ ‫הדחי ‪ /‬המידות הכלליות בכל מישור‪ /‬המנוע ‪ /‬המשוטים ‪ /‬המפרשים ‪.‬‬ ‫הערה‪ :‬המהירות המרבית של כלי שיט ‪ ,‬בתלות ב " אורך‪ -‬קו‪ -‬המים " ( ה אורך ה מירבי תלוי‬ ‫בשוקע )‪ LWL = Length of Water Line .‬נתנת לחישוב מקורב לפי הנוסחה‪-:‬‬ ‫½‬ ‫‪ HULL SPEED = 1.34 X L.W.L‬כש‪ LWL -‬הוא אורך קו המים ביחידות רגל ( ‪) Feet‬‬ ‫והתוצאה בקשרים ‪ .‬תחילה יש להוציא שורש ריבועי ) ½ =√ ) של ‪ LWL‬ואז להכפיל ב‪. 1.34 -‬‬ ‫ב ‪ .‬בהבט שבשליטתו ובחירתו של המשיט ‪:‬‬ ‫‪1. Selected Speed.‬‬ ‫‪2. Cruising Speed.‬‬ ‫‪3. Economic Speed.‬‬ ‫‪4. Safe Speed.‬‬ ‫‪5. Maximum Speed (Full Ahead).‬‬ ‫‪6. Minimum Speed (Dead Slow).‬‬ ‫‪7. Emergency Speed.‬‬ ‫‪8. Crash Speed.‬‬ ‫‪9. Maximum Reverse Speed.‬‬ ‫ג‪ .‬בהבט שהוא תוצאה של תנאי הסביבה בשלוב עם בחירתו של המשיט‪:‬‬ ‫‪Run between two fixes (“True speed”).‬‬ ‫‪Speed through the Water.‬‬ ‫‪LOG Speed.‬‬ ‫‪Velocity Made good/Speed Made Good.‬‬ ‫‪Velocity over Ground/Speed Over Ground‬‬ ‫‪Speed to Reach Destination.‬‬ ‫‪Speed of Advance.‬‬ ‫‪Speed/Velocity Over Ground = SOG/VOG‬‬ ‫‪Speed/Velocity Made Good = SMG/VMG‬‬ ‫המהירות בפועל ( ‪ ) Made Good/Over Ground‬של כלי השייט בין שני אתרים ‪ ,‬כאשר ישנה‬ ‫השפעת רכיבי זרם ורוח שעם התנועה או נגדה ‪ .‬כאשר רכיב הזרם עם התנועה =‪SOG‬‬ ‫‪ Vessel Speed + Tide‬ונגד התנועה ‪SOG= Vessel Speed - Tide Speed‬‬ ‫קרא שנית פיסקת הפתיחה של הפרק ‪ ,‬לעיל ‪ ,‬מהירות התנועה של כלי השיט‪.‬‬ ‫‪ Speed to Reach Destination‬ו‪ Speed of Advance -‬הן מהירויות שיש לחשב אותן‬ ‫בנוסף לקריאת המהירות ממדידה כל שהיא ‪ .‬זה משום ‪ ,‬שהנתיב אל היעד אינו בהכרח הקו‬ ‫הישר של הקורס במפה; ומכך עולות מייד השאלות ‪ :‬א ) באיזו מהירות מתקרבים ליעד ?‬ ‫ב ) באיזו מהירות יש לנוע כדי להגיע בזמן נקוב ? מאז השימו ש ב‪ GPS -‬הוא מבצע את‬ ‫אגירת המיד ע‪ ,‬המיצו ע והצגת התוצאות‪.‬‬ ‫הערה‪ - :‬אחד הנתונים ‪ ,‬שקשורים למהירות כ לי שיט‪ ,‬הוא המרחק הקטן ביותר שיעבור ‪,‬‬ ‫ממצב של מהירות מרבית עד לעצירה מלאה ( עם או בלי שלוב מדחף לאחור )‪.‬‬ ‫‪ – FIX‬אתר בזמן מסויים ‪ ,‬ובנקודת החיתוך של שניים או יותר ‘ קוי‪ -‬אתר ' ‪ .‬האתר מתקבל‬ ‫על ידי שרטוטו במפה ‪ ,‬או קריאתו בתצוגה כל שהיא‪.‬‬ ‫‪ -RUNNING FIX‬אתר המתקבל על ידי הסעה מקבילה של תכווין או טווח ‪Transferred -‬‬ ‫‪ Position Line‬וקבלת נקודת חיתוך עם תכווין או טווח אחר‪.‬‬ ‫‪ ( – (DEAD RECKONING) DR‬אתר מקורב ‪ /‬מוקש ) אתר המופק בהקצאת הדרך ‪,‬‬ ‫מהאתר האחרון‪ ,‬שסומן במפה ‪ ,‬על הקורס המתוכנן במפה‪ .‬הדרך מופקת מהכפלת‬ ‫מהירות מקורבת ( ‪ , ) LOG‬ב הפרש ה זמן ‪ ,‬ש חלף מ האתר‪ ,‬שעודכן לאחרונה ‪ ,‬לשעת רשום‬ ‫האתר החדש‪ .‬כמובן נתן לקרא ‪ ,‬ישירות ממד‪ -‬דרך ‪ ,‬שתצוגתו נרשמה בתחילת הקטע ‪.‬‬ ‫מבחינת " ימאות טובה " יש לעדכן את ה‪ DR -‬במקרים הבאים ‪-:‬‬ ‫‪ ‬בסיום כל משמרת‪ -‬ים ‪ .‬והרעיון הוא ‪ ,‬שתהיה רציפות בתעוד מקום הספינה ‪ ,‬למקרה‬ ‫של חלופי עמדות או משמרות ( בצי סוחר כל ‪ 4‬שעות)‪.‬‬ ‫‪ ‬לאחר כל שנוי כיוון או מהירות‪.‬‬ ‫‪ ‬לאחר כל הפקת אתר ‪ FIX‬או ‪. RUNNING FIX‬‬ ‫‪ ‬לאחר כל הפקה ושרטוט של קו אתר כל שהוא ( ‪. ) LOP Line Of Position‬‬ ‫‪520 5‬‬ ‫‪DR/FIX‬‬ ‫‪11‬‬ ‫‪11‬‬ ‫אורך ‪ /‬משך זמן המסע‬ ‫קריאת מד דרך ‪ 20‬מילים ימי ים‬ ‫אתר רשום בתחילת משמרת בשעה‬ ‫או ‪-:‬‬ ‫קריאת מד מהירות ( לדוגמה ‪ 5‬קשר ) ‪ X‬הפרש הזמן ( בדוגמה‬ ‫‪DR‬‬ ‫סיום משמרת‬ ‫‪11‬‬ ‫‪14‬‬ ‫‪ 4 = 11 11-14 11‬שעות )= ‪ 21‬מיל ‪.‬‬ ‫ובמפה ‪-:‬‬ ‫‪ 21‬מיל‬ ‫צפון המפה‬ -:‫רשימה של הסימוני ם הבסיסיים והמקובלים בעבודת מפה‬ True Course Compass Course or 090 0 T Compass/Magnetic/True Course Over Ground Water Track Ground Track Tidal Stream or Current Position Line (Line Of Position= LOP) or Transferred Position- Line or also for Bearings Range Position- Line Clearing- Line NL 085 0 C Not Less 085 0 Compass Dead Reckoning Position = DR Estimated Position = EP or Electronic instrument Position FIX RADAR Position .‫ ספרות‬4 -‫ליד כל סימוני תכווינים ואתרים חובה לרשום את השעה ודקות ב‬ ‫ בקשר למהירות כלי‬. ‫ שהם זוויו ת או קשורים לזווי ת‬, ‫עד כאן הוצגו מושגים והגדרות‬ ‫ אך בגלל חשיבותו ל מושגי ההמשך‬, ‫ אף הוא קשור בזוית‬, ‫ אוזכר המושג וקטור‬, ‫השייט‬ .‫תובא תמצית להסבר השימוש בו‬ ‫' איחוד כוחות ' ‪ -‬ו וקטור ‪ -‬ופעולות מתמטיות ב ווקטורים ‪.‬‬ ‫וקטור במהותו הוא סמל ‪ ,‬שמאפשר תאור כמותי של כוחות על דף כתיבה ‪ .‬תאור כמותי ‪ ,‬לא‬ ‫רק כמספר יחידות ‪ ,‬אלא בתוספת מאפייני ם אחרים ‪ .‬הווקטו ר מסומן בצורה ●‬ ‫צורה זו כוללת את המרכיבים הבאים ‪-:‬‬ ‫‪ . 1‬נקודת אחיזה ● שבה " אוחז " ה ו וקטור את הגוף עליו הוא פועל‪.‬‬ ‫אשר לאורכו פועל הכו ח באחד הכיוונים ‪.‬‬ ‫‪ . 2‬קו פעולה‬ ‫‪ . 3‬כיוון ‪ ,‬כל שהוא‪ ,‬שאליו דוחף או מושך הכ ו ח ‪.‬‬ ‫‪ . 4‬מספר היחידות הכלולות באורכו מנקודת האחיזה עד קצה חץ הכיוון ‪ .‬לדוגמה אם‬ ‫אז ‪ 5‬קמ " ש יהיו‬ ‫יחידת מהירות של ‪ 1‬ק " מ בשעה תהיה‬ ‫מוסכמות יסוד ביחס לפעולת כוחות המסומנים כוקטורים באותו מישור או מרחב‪-:‬‬ ‫א ‪ .‬קווי הכו ח אינם חותכים זה את זה‪.‬‬ ‫ב ‪ .‬נקודת האחיזה פועלת על חומר או גוף קשיח ‪ .‬הדיון של השפעת כוחות על חומרים‬ ‫רכים הוא מחוץ למסגרת זו ‪ ,‬אך אפשר להתייח ס לכל חלקיק‪ ,‬של גוף רך‪ ,‬כקשיח ‪.‬‬ ‫ג ‪ .‬נתן לה סיע את מקום הווקטו ר לאורך קו הפעולה שלו‪ ,‬אחורה וקדימה‪.‬‬ ‫ד ‪ .‬נתן להעתיק במקביל את קו הפעולה ‪ ,‬לכל מקום משני צדדיו‪ ,‬של קו הפעולה‪.‬‬ ‫ה‪ .‬נתן לפרק וקטור ל רכיבים ‪ ,‬ונתן להרכיב מספר וקטורים לווקטו ר שקול אחד‪ .‬בלשון‬ ‫אחרת ‪ ,‬אפשר לבצע‪ ,‬פעולות מתמטיות שונות עם וקטורים ‪ ,‬אך לנדרש כאן ‪ ,‬מספיק‬ ‫היד ע של חיבור וחיסו ר של וקטורים שפועלים על אותו גוף ‪ .‬פעולות אלה חיוניות‬ ‫להבנת המושגים והפרקים ‪ ,‬שבהמשך ותלמדנה להלן ‪.‬‬ ‫אילו " גדלים וקטורים " פוגשים בנושאי הספנות ? בהכללה התשובה היא כל הסוגים ‪,‬‬ ‫משום שכל טכנולוגיה חדישה קיימת במבנה ובמכלולים של כלי שייט ‪ .‬אך אלה השגורים‬ ‫ביותר הם ‪-:‬‬ ‫וקטור מהירות כלי שייט ביחידות של קשר = מייל ימי בשעה לדוגמה ‪.‬‬ ‫וקטור מהירות הרוח ביחידות של קשר = מייל ימי בשעה לדוגמה‪.‬‬ ‫וקטור מהירות ה זרם ביחידות של קשר = מייל ימי בשעה לדוגמה‪.‬‬ ‫וקטור כוח הדחף של להב מדחף המנוע‪.‬‬ ‫וקטור כוח הלחץ של לוח ההגה ‪ ,‬ידיות ומנופים לסוגיהם ‪.‬‬ ‫וקטור כוח הקידום של מפרש‪.‬‬ ‫וקטור כוח ההתנגדות לסטיה של קוער הספינה או ה " חרב " )‪. (Centerboard/Keel‬‬ ‫הוקטורים בציר הסיבוב ומרכז הלחץ של מבנה כלי השייט‪ ,‬אשר יוצרים מומנט סיבוב ‪ ,‬אם‬ ‫אינם על אותו קו אנכי למשור התנועה‪.‬‬ ‫וקטור כוח המתיחות של חבלים כבלים ושרשרות‪.‬‬ ‫וקטור של כוח ציפה‪ ,‬דחי והתנגדות לתנועת מים‪.‬‬ ‫כמו בן ישנם עוד רבים ‪ ,‬אך גם רשימה זו ארוכה מההתייחסות שדרושה בשגרת השיט‪.‬‬ ‫פעולות החישוב והפתירה ‪ ,‬שבין שני וקטורים ‪ ,‬מובאות ב עקר לצורך עבודת מפה‪ ,‬שהיא‬ ‫השימוש הנפוץ ביותר ‪ ,‬וכמעט היחיד ‪ ,‬אשר א ליו ידרש משיט ספינה‪.‬‬ ‫בעיה ‪ – 1‬חבור שני וקטורים על אותו קו פעולה‪.‬‬ ‫כלי שייט נע ‪ ,‬על קורס נתון‪ ,‬בכח מנוע במהירות ‪ 7‬קשר; מאחוריו מתחילה לנשוב רוח‬ ‫במהירות ‪ 15‬קשר ‪ ,‬והיא גורמת לתוספת מהירות של ‪ 3‬קשר‪ .‬יש להבין‪ ,‬שראשית ‪15 -:‬‬ ‫קשר ‪ ,‬של מהירות הרוח ‪ ,‬אינם מוסיפים ‪ 15‬קשר למהירות ספינת מנוע ‪ ,‬ואף לא לספינת‬ ‫מפרש ‪ .‬שנית‪ -:‬אין דרך מדוייקת ‪ ,‬להעריך מראש את התרומה של הרוח למהירות‪ ,‬אלא על‬ ‫ידי מדידה חוזרת ‪ .‬מסיבות אלה הבעיה ‪ ,‬כאילו פתורה מראש‪ ,‬בעצם קריאת מד המהירות‬ ‫של הספינה ‪ .‬לצורך פתרון כללי של חבור שני וקטורים על אותו קו פעולה מה שנעשה הוא‪-‬‬ ‫‪ 3‬קשר ‪ 7 +‬קשר‬ ‫הסכום = " ה וו קטור השקול "‬ ‫= ‪ 11‬קשר‬ ‫הערה‪ :‬השימוש במלה " שקול " בא ל מקרה ‪ ,‬שהוקטורים אינם על אותו קו פעולה ‪ ,‬כשאז‬ ‫התוצאה אינה סכום אלגברי פשוט ‪ ,‬אלא " סכום וקטורי " כפי שנראה בהמשך‪.‬‬ ‫בעיה ‪ – 2‬חיסו ר שני וקטורים על אותו קו פעולה‪.‬‬ ‫כלי שייט נע במהירות ‪ 5‬קשר ביחס לקרקע ‪ ,‬ונכנס לאזור שבו רכיב הזרם הנגדי הוא ‪1.5‬‬ ‫קשר ‪ .‬לכאורה גם כאן היה מספיק לקרא את התצוגה של מד המהירות‪ .‬אך רוב מדי‬ ‫המהירות‪ ,‬הנפוצים בכלי שייט ‪ ,‬מציגים את המהירות ביחס למים ולא ביחס לקרקע ‪ .‬באופן‬ ‫כללי ‪ ,‬החסור מבוצע על ידי הקצאת הווקטו ר המחסר‪ ,‬מקצהו ועל הוקטור המחוסר ‪.‬‬ ‫‪ 1.5‬קשר‬ ‫‬‫‪ 5‬קשר‬ ‫השקול יהיה ‪ 3.5‬קשר‬ ‫בכוון התנועה‪.‬‬ ‫‪3.5‬‬ ‫בעיה ‪ 2‬א – זרם נגדי לתנועת הספינה‪.‬‬ ‫במקרה שהמחסר גדול מהמחוסר ‪ ,‬לדוגמה מפרשית שנעה ברוח חלשה במהירות של ‪3‬‬ ‫קשר ‪ ,‬ביחס לקרקע‪ ,‬ובזרם נגדי של ‪ 3.5‬קשר‪.‬‬ ‫‪ 3‬קשר‬ ‫ההפרש השקול הוא ‪ 1.5‬קשר‬ ‫בכוון הזרם ‪ ,‬כלומר הפוך לקורס‪,‬‬ ‫כך שהספינה נעה לאחור ביחס‬ ‫למטרתה‪.‬‬ ‫‪ 3.5‬קשר‬ ‫בעיה ‪ 2‬ב ‪ -‬מדידת מהירות הרוח תוך תנועת הספינה‪.‬‬ ‫בעיה זו מוצגת‪ ,‬כדי למנוע בלבול בין קריאת מהירות הרוח ובין השפעתה על מהירות כלי‬ ‫השייט ביחס לקרקע‪.‬‬ ‫ישנו מבחר גדול של מכשירים המשמשים למדידת מהירות הרוח ‪ ,‬לכן ‪ ,‬לצורך הדוגמה כאן ‪,‬‬ ‫נתייחס לאותם דגמים בהם וקטור מהירות הרוח פועל על גל גל כנפיים ‪ ,‬מסוג כל שהוא ‪.‬‬ ‫הבעיה היא למצו א מה תהיה קריאת מד הרוח ‪ ,‬כאשר הספינה בתנועה ? אנו מניחים ‪,‬‬ ‫שמד‪ -‬הרוח מגיב לווקטו ר מהירות הרוח שעל קו התנועה של הספינה ‪ ,‬כלומר גם אם הכוון‬ ‫הכללי של הרוח נמצא בזוית לקו זה ‪ ,‬אנו מתחשבים רק ברכיב שמוסיף או גורע מקריאת‬ ‫מד – מהירות הרוח‪.‬‬ ‫הערות הרחבה ביחס לבעיות ‪ 1‬ו‪-: 2 -‬‬ ‫לצורך פתרון ‪ 1‬ו‪ 2 -‬ה סע נו‪ ,‬לאורך קו‪ -‬הפעולה ‪ ,‬את נקודת האחיזה של וקטור אחד אל קצה‪,‬‬ ‫חץ הכיוון ‪ ,‬של וקטור שני ‪ .‬לדוגמה בחיסו ר ‪A-B‬‬ ‫‪B‬‬ ‫ההפרש ‪C‬‬ ‫‪A‬‬ ‫כמו כן ‪ ,‬כשרוצים לקבל את השקול במקום מסוים ‪ ,‬על דף או במפה הימית‪ ,‬מותר להעתיק‪,‬‬ ‫ולאחד לקו אחד ‪ ,‬קוו י פעולה ‪ ,‬של וקטורים הנמצאים על קווי פעולה מקבילים ‪ ( ,‬הזוית‬ ‫העתקה במקביל הסעה השקול‬ ‫בינ י הם היא ‪. ) 1 1‬‬ ‫לדוגמה הרכבת שני וקטורים ‪:‬‬ ‫שלבי החיבור‬ ‫וקטור ‪1‬‬ ‫‪+‬‬ ‫‪2+1‬‬ ‫וקטור ‪2‬‬ ‫במפה הימית ההעתקה במקביל וההסעה לאורך קו הפעולה מבוצעת במספר שיטות‬ ‫ובעזרת מבחר מכשירים ‪ ,‬אך הנפוצים ביותר הם מחוגה וסרגל‪ -‬מקביל ‪ ,‬או זוג משולשים ‪.‬‬ ‫נדרשת תשומת לב מיוחדת ‪ ,‬כשמתבקשים לפתור בעיות של מציאת מהירות הרוח ‪ ,‬על כלי‬ ‫שייט בתנועה‪ ,‬ו השפעת מהירות הרוח על מהירות כלי השייט ‪-:‬‬ ‫א ) מהירות " רוח הפנים " של כלי שייט זהה למהירותו וכיוונה מנוגד לכוון‬ ‫תנועתו‪ ,‬וניתנ ת למדידה כאשר אין רכיבי רוח אחרים‪.‬‬ ‫ב ) רוח עם כוון תנועתו של כלי שייט אינה תורמת את מל ו א מהירותה למהירות‬ ‫כלי השייט גם לא במפרשית ‪.‬‬ ‫בעיה ‪ – 3‬הרכבה של שני ו וקטורים ‪ ,‬שקווי הפעולה שלהם אינם מקבילים ‪ ,‬כלומר ה זוית‬ ‫בינם שונה מ‪ . 1 1 -‬קיימות מספר שיטות להרכבה או פרוק של וקטורים ‪ ,‬שאינם מקבילים ‪,‬‬ ‫יש ומכנים אותן בהכללה תחת השם " חיבור וקטורי " ‪ ,‬גם אם מבצעים פעולת חיסור או‬ ‫פרוק ‪ .‬ישנן שיטות " חישוביות " הנותנות ערכים מספריים של יחידות וכיוון ; יש שיטות‬ ‫שהן " שירטוטיות " ( גראפיות ) וישנן שיטות שהן שילוב של חישוב ושירטוט ‪ .‬לצורך‬ ‫ההסברים שקשורים לעבודת מפות ותנועת כלי שייט נפוצות השיטות השירטוטיות ‪ ,‬שהן‬ ‫שתיים‪ :‬א ) שימוש במערכת צירים ישרת זווית ( ציר ‪ X‬אופקי וציר ‪ 81 1 Y‬לציר ‪.) X‬‬ ‫ב ) שיטת " מ קבילית הכוחות " ‪ ,‬אשר היא מעין קצור דרך של שיטה ( א )‪ .‬נאזכר שנית ‪,‬‬ ‫ש הדיון מותנה בחמש מוסכמות היסוד ‪ ,‬שבתחילת הפרק ‪ ,‬ובעקר לכך שאנו מתייחסים‬ ‫לפעולת וקטורים על גופים קשיחים ‪.‬‬ ‫שיטה א ‪ -‬מערכת צירים ישרת זווית‪.‬‬ ‫נתונים וקטור ‪A‬‬ ‫ווקטור ‪B‬‬ ‫שלב ראשון נשרטט מערכת ישרת ‪ -‬זווית במקום ( על הנייר או המפה )‪ ,‬שבו דרושה‬ ‫התוצאה ‪ ,‬ונעתיק את הוקטורים ל " נקודת הראשית " ( נקודת החיתוך שבה ‪ 1 = X‬ו ‪.) 1 = Y‬‬ ‫‪Y‬‬ ‫רבע ‪ X‬חיובי ו‪ Y -‬שלילי‬ ‫רבע ‪ X‬שלילי ‪ Y‬חיובי‬ ‫‪X‬‬ ‫רבע ‪ X‬חיובי ‪ Y‬שלילי‬ ‫רבע ‪ X‬שלילי ‪ Y‬שלילי‬ ‫שלב שני‪ ,‬נבצע פעולת " הטלה " של כל וקטור על צירי המערכת ‪ ,‬כלומר כל נקודה של כל‬ ‫אחד מהוקטורים תוטל הן על ציר ‪ X‬והן על ציר ‪ . Y‬היות ויש אין‪ -‬סוף נקודות ‪ ,‬מסתפקים‬ ‫רק בחלוקה ‪ ,‬שמספקת את הדיוק השימושי‪.‬‬ ‫‪Y‬‬ ‫רבע ‪ X‬שלילי ‪ Y‬חיובי‬ ‫רבע ‪ X‬חיובי ו‪ Y -‬שלילי‬ ‫‪X‬‬ ‫רבע ‪ X‬שלילי ‪ Y‬שלילי‬ ‫רבע ‪ X‬חיובי ‪ Y‬שלילי‬ ‫שלב שלישי נניח‪ ,‬שהאדום מייצג מהירות כלי שייט‪ ,‬בקשרים וכיוון במעלות ביחס ל‪, Y -‬‬ ‫והכחול מהירות וכיוון זרם באותן יחידות‪ .‬ערך הזוויות מקורב‪ ,‬רק לצורך ההדגמה‪.‬‬ ‫‪Y‬‬ ‫רבע – ‪ X‬ו ‪Y +‬‬ ‫רבע ‪ X +‬ו ‪Y +‬‬ ‫‪45 0‬‬ ‫‪X‬‬ ‫‪231 1‬‬ ‫רבע ‪ X +‬ו – ‪Y‬‬ ‫קבלנו ‪ + 7‬יחידות של הכחול על ציר ה ‪X‬‬ ‫ו ‪ -5,5‬של האדום ‪ ,‬והסכום האלגברי הוא‬ ‫‪ +7 – 5,5 = +1,5‬כלומר ‪ 1,5‬על ציר ה‪. X +‬‬ ‫רבע – ‪ X‬ו – ‪Y‬‬ ‫שלב רביעי‬ ‫‪Y‬‬ ‫רבע – ‪ X‬ו ‪Y +‬‬ ‫רבע ‪ X +‬ו ‪Y +‬‬ ‫‪X‬‬ ‫רבע – ‪ X‬ו – ‪Y‬‬ ‫רבע ‪ X +‬ו – ‪Y‬‬ ‫ישנן ‪ + 6‬יחידות של הכחול על ‪Y +‬‬ ‫ו ‪ -12‬יחידות של האדום והסכום האלגברי‬ ‫יהיה ‪ +6 -12 = -6‬כלומר ‪ 6 -‬על ציר ‪. Y -‬‬ ‫שלב חמישי הווקטור שווה הערך‪ ,‬ה " שקול " ‪ ,‬לרכיבים האדום והכחול ‪ ,‬שהתקבל מהשלבים‬ ‫הקודמים ‪ , ,‬יהיה החץ הירוק‪.‬‬ ‫‪Y‬‬ ‫רבע – ‪ X‬ו ‪Y +‬‬ ‫רבע ‪ X +‬ו ‪Y +‬‬ ‫זווית הכיוון של כלי השייט = ‪α + 81 1‬‬ ‫‪81 1‬‬ ‫‪+1.5‬‬ ‫‪X‬‬ ‫‪α‬‬ ‫רבע – ‪ X‬ו – ‪Y‬‬ ‫רבע ‪ X +‬ו – ‪Y‬‬ ‫‪-6‬‬ ‫בעבודת מפות‪ ,‬מודדים עם מחוגה את מספר‬ ‫יחידות האורך על סולם היחידות של המפה‪,‬‬ ‫ובעזרת מד זווית את הכיוון ביחס לצפון ( ציר ‪.) Y‬‬ ‫שיטה ב – חישוב במשולש ישר ז ו וית‬ ‫לקוראים ‪ ,‬שיודעים את הדרך החישובית ‪ ,‬מספר היחידות מהן מורכב הווקטור ( הירוק )‬ ‫‪ ,‬הפעולה היא של חישוב‬ ‫=‬ ‫=‬ ‫מתקבל מהחישוב ‪= 6.2 -:‬‬ ‫אורך היתר ‪ ,‬במשולש ישר זווי ת ‪ ,‬על סמך משפט בהנדסת המישור‪ ,‬הקרוי " משפט‬ ‫פיתגורס "‪ .‬במקרה‪ ,‬שדנים במהירות בים ‪ ,‬היחידות הן " קשר " וכותבים ‪. 6.2knots‬‬ ‫ו את הז ו וית ‪ α‬נמצא מתוך ? = ‪ ( tan. α‬טנגנס של זווי ת ‪ ,‬במשולש ישר זווי ת ‪ ,‬הוא היחס‬ ‫המספרי שבין הניצב שמול הזוית והניצב שסמוך לזווי ת ‪ ).‬במקרה שבדוגמה ‪6 : 1.5 = 4‬‬ ‫ומתוך לוח‪ ,‬או מחשבון ‪ ,‬מוצאים שעבור ‪ tan. α = 4‬מקבלים ‪ . α = 76 0‬היות ובמפה הימית‬ ‫כיוון כלי שיט נמדד מהצפון ( ציר ה‪ ) Y -‬עם כיוון השעון‪ ,‬כיוון כלי השייט במקרה שבדוגמה‬ ‫הוא ‪ . 90 0 + α = 90 0 + 76 0 = 166 0‬ובמפה הימית מסמנים ‪-:‬‬ ‫‪166 0 /6.2kts‬‬ ‫לפי אחת המוסכמות ‪ ,‬מסמנים את הקורס מעל הקרקע ‪ COG‬באדום אך מקובל כל סימון‪,‬‬ ‫שיאזכר את העובדה ‪ ,‬שאין זה הקורס המתוכנן ‪ ,‬אלא תוצאה של השפעת הזרם ‪.‬‬ ‫‪Y‬‬ ‫‪1.5‬‬ ‫‪X‬‬ ‫‪α‬‬ ‫‪6‬‬ ‫מעתיקים את השקול למקום הספינה‬ ‫במפה הימית ומעתה הוא " הנתיב‬ ‫‪0‬‬ ‫בפועל " ) מעל ה קרקע ‪ COG‬או ‪166 /6.2kts ) CMG‬‬ ‫הערה ‪ :‬ערך הזוית מחולץ מתוך ה‪ tan. -‬היות ופונקציות ‪ sin.‬ו‪ cos. -‬תלויות בערך המחושב של היתר ‪,‬‬ ‫ש עלול להיות שגוי ‪ ,‬שלא כמו ה‪ , tan. -‬שמוגדר מתוך ערכים נתונים ‪ ,‬של הניצבים ‪.‬‬ ‫שיטה ג " מקבילית הכוחות " ‪-:‬‬ ‫זו השיטה השרטוטית הנפוצה ב " מפת מרקטור " ‪ ,‬אשר ב ה קווי האורך מאונכים לקווי‬ ‫הרוחב ‪ ,‬ולכן באים במקום המערכת ישרת הזווית של ‪ X‬ו‪ . Y -‬כך ‪ ,‬כל אתר במפה הוא‬ ‫" נקודת ראשית " או " נקודת הפתרון " במערכת ישרת זווית ‪ .‬ובאופן מיידי נתן להגדיר כל‬ ‫נקודה ‪ ,‬כנקודת החיתוך של קו רוחב עם קו אורך שנמדדו עם סרגל ומחוגה ללא כל‬ ‫חישוב ‪ .‬היות ולכל מפה ישנו קנה‪ -‬מידה ‪ ,‬שלפיו היא שורטטה‪ ,‬משתמשים ביחידות האורך‬ ‫של המפה לשרטוט גודלם של הווקטורים ‪ ,‬בכך אין צורך להעתיק את הווקטורים ל נקודת‬ ‫הראשית של מערכת שמשורטטות בה היחידות ‪ ,‬ו בהמשך לנצל את תכונות הצורה‬ ‫ההנדסית המכונה " מקבילית "‪ .‬ההגדר ה הכללית של צורה זו היא ‪ -:‬מצולע בעל ארבעה‬ ‫הצורות ריבוע‪ ,‬מלבן ומעוין הן‬ ‫צלעות‪ ,‬אשר כל שתי צלעות נגדיות מקבילות‪.‬‬ ‫מקרים מיוחדים של מקבילית ‪ ,‬עם אותן תכונות ‪.‬‬ ‫כהערת הקדמה יאמר ‪ ,‬שהשימו ש במקבילית אינו המצאה ‪ ,‬בפני עצמה ‪ ,‬אלא שימו ש ש גזור‬ ‫משתי השיטות הקודמות ‪ ,‬ומהוות מעין " קיצור דרך " המסתמך עליהן ‪ .‬על ידי סימון צלעות‬ ‫המקבילית והאלכסונים כ ו וקטורים ‪ ,‬נתן לבצע את פעולות החיבור והחיסור שבין גדלים‬ ‫ווקטורים מבלי להעתיק אותם לנקודת הראשית של מערכת ישרת זווית‪ .‬פעולה זו הופכת‬ ‫את המקבילית למה שמכונה " מקבילית הכוחות "‪.‬‬ ‫לדוגמה כלי שיט שמסומן במפה ‪090 0 7kts‬‬ ‫נמצא באזור בו פועל זרם‬ ‫‪225 0 3kts‬‬ ‫כ ש הדרישה היא למצו א את השקול ‪ ,‬שיתאר את תנועת כלי השייט בפועל ‪ .‬הפתרון לזה ‪ ,‬או‬ ‫לכל הרכבה אחרת של שני וקטורים‪ :‬מסיעים את אחד הוקטורים או את שניהם למקום בו‬ ‫דרוש הפתרון ‪ ,‬ומקצים בקצהו של האחד את נקודת האחיזה של השני כהמשכו‪.‬‬ ‫מתקבלת " מקבילית כוחות " ‪ ,‬שהאלכסון הקצר שלה ( האדום ) הוא הווקטור השקול‬ ‫המבוקש ‪ .‬רואים מייד שנתן להזניח את ציור המקבילית‪ ,‬ולהסתפק בסגירת " משולש‬ ‫הכוחות "‪.‬‬ ‫אם הזרם היה ‪-:‬‬ ‫‪045 0 3kts .‬‬ ‫השקול י היה האלכסון הארוך של המקבילית ‪ ,‬בלשון אחרת ‪ ,‬הצלע שמשלימה למשולש ‪.‬‬ ‫הערות והארות חשובות ‪:‬‬ ‫‪ . 1‬הרכבה ופרוק וקטורים ‪ ,‬בהקשר של " עבודת מפה "‪ ,‬נעשה עם יחידות מהירות של‬ ‫קשר ‪ ,‬כלומר מיל ימי ב‪ 1 -‬שעה‪ ,‬זה אומר ‪ ,‬שכל הווקטורים מייצגים שעה אחת של‬ ‫מסע כלי השייט‪ ,‬ויש לשמור על קנה מידה אחיד של כל המרכיבים ‪ ,‬בייחוד כאשר ‪,‬‬ ‫לבהירות השרטוט ‪ ,‬מכפילים ‪ ,‬או משלשים את ‪ ,‬גודל היחידות ‪ .‬לאחר מציאת פתרון ‪,‬‬ ‫יש לחזור לקנה המידה של המפה‪.‬‬ ‫‪ . 2‬השאלה ‪ ,‬שמתבקשת מיידית לאחר מציאת ה " נתיב ב פועל " ‪ ,‬שבהשפעת הזרם ‪ ,‬היא‬ ‫איך למצוא את הווקטור ‪ ,‬שייצג את תנועת כלי השייט כדי ש" בפועל " ימשיך לנוע‬ ‫בנתיב אל היעד‪ .‬בלשון אחרת " יתנגד לזרם " ‪ . Allowing for current ,‬בספרות‬ ‫ההדרכה ושאלוני בחינות ‪ ,‬הבעיה מוצגת כמציאת ה‪CTS = Course To Steer -‬‬ ‫( השלמות בשלבי הכנה )‬