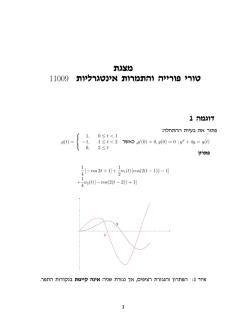
‫אם הגבול באגף‬
.‫ימין קיים וסופי‬

D
f ( x, y, z ) dV  lim
Vk 0
 f (x , y , z
k
k
k
k
) Vk
3
‫ פונקציה אינטגרבילית על התיבה‬f ‫תהי‬
B  [a, b]  [c, d]  [p, q]
‫אזי‬
q d b
 f(x, y, z) dx dy dz     f(x, y, z) dx dy dz 
B
p c a
q b d
    f(x, y, z) dy dx dz 
p a c
b q d
    f(x, y, z) dy dz dx
a p c
4
:1 ‫דוגמא‬
I 
4
1
4 2 e
J 

1 1 1
3

4
0 1
( x  yz ) dx dy dz
:2 ‫דוגמא‬
yz
dxdydz
x
5
‫תכונות של אינטגרלים משולשים‬
1)  cf ( x, y, z )dxdydz  c  f ( x, y, z )dxdydz
R
‫ קבוע‬c
R
2)  [ f ( x, y, z )  g ( x, y, z )]dxdydz 
R
  f ( x, y, z )dxdydz   g ( x, y, z )dxdydz
V
V
3)  f ( x, y )dxdy   f ( x, y, z )dxdydz   f ( x, y, z )dxdydz
V
V1
V2
6
‫חישוב כללי של אינטגרל משולש‬
 f ( x, y, z )dxdydz
v
z2 ( x , y )
 dxdy  f ( x, y, z )dz
D
z1 ( x , y )
7
‫‪dxdydz‬‬
‫‪,‬‬
‫‪3‬‬
‫‪‬‬
‫) ‪(1  x  y  z‬‬
‫‪V‬‬
‫חשב אינטגרל משולש‪,‬‬
‫כאשר תחום ‪ V‬חסום ע''י‬
‫מישורים הבאים‬
‫‪x  y  z  1,‬‬
‫‪x  0, y  0, z  0.‬‬
1xy
dxdydz
d(x yz 1)
 dxdy

3 
3

(1x yz) D
(1x yz)
V
0
1xy
1 1
1 
1
1
dxdy 
dxdy    
 
2
2
2 D 4
(1x y) 
2 D (1x yz) 0
1x
1x
1
1
1 
1 y
1 
dy  
 dx
 dx  
2
2 0 0  4 (1x y) 
2 0  4 1x y0
1
1
1
1 1 x 1
1 
  
 
dx 
2 0 4
2 1 x 
1
 1 (1 x) 1 1

 
 

x

ln(
1

x
)
 8

2
4
2

0
2
5
1 1 1
1
 ln 2    ln 2  .
16
4 16 2
2
V   dxdydz
V
‫נוסחה הכללית לחישוב נפח במרחב ללא תלות בקואורדינטות‬
‫‪V   dv‬‬
‫‪V‬‬
‫חשב נפח של הגוף החסום‬
‫עיי' משטחים‬
‫‪yx ,‬‬
‫‪z  y,‬‬
‫‪2‬‬
‫‪z  y  2.‬‬
y  1 ‫נמצא עקומת החיתוך של שני משטחים‬
2 y
2 y
V  dxdydz dxdy  dz   z
V
1
D
y
y
D
dxdy (2  2 y)dxdy
D
y
1
1
 2(1 y)dy dx 2(1 y) x  y dy 2(1 y) 2 ydy
y
0
 y
0
0
1
 4
0


2
2

y  y dy  4 y  y
5
3
3
3
2
5
2
1

16
  .

 0 15
D ‫ נהפך לתחום‬uvw ‫ במרחב‬G ‫נניח שהתחום‬
xyz
‫ע"י העתקות גזירות‬
‫במרחב‬
x  g (u , v, w), y  h(u, v, w), z  k ( x, y, z )
H ‫ מגדירה פונקציה‬x, y, z ‫ של המשתנים‬F ‫כל פונקציה‬
u , v, w: ‫של המשתנים‬
H (u , v, w)  F ( x, y, z )  F ( g (u , v, w), h(u , v, w), k (u , v, w))
‫אזי‬
 ( x, y , z )
D F ( x, y, z ) dx dy dz G H (u, v, w) (u, v, w) du dv dw

| J ( u ,v , w )|
16
:‫האינטגרל‬

D
F ( x, y, z ) dx dy dz   H (u , v, w)
 x

 u
 ( x, y, z )  y

 (u , v, w)  u
 z

 u
G
x
v
y
v
z
v
x 

w 
y 
w 
z 

w 
 ( x, y , z )
du dv dw
 (u , v, w)

| J ( u ,v , w )|
‫כאשר המטריצה‬
‫נקראת היקוביאן של הטרנספורמציה )החלפת‬
(‫הקואורדינטות‬
17
‫קואורדינטות גליליות‬
‫‪x  r cos ‬‬
‫‪y  r sin ‬‬
‫‪zz‬‬
‫‪18‬‬
19
‫נתונה פונקציה ‪ f‬של שלושה משתנים )‪ (x,y,z‬בתחום‬
‫חסום וסגור ‪ D‬במרחב ‪ .R3‬אזי‪:‬‬
‫‪f ( x, y, z ) dV   f (r cos  , r sin  , z ) r dz dr d‬‬
‫‪D‬‬
‫‪20‬‬
‫‪‬‬
‫‪D‬‬
‫נפח של הגוף בקואורדינטות גליליות‬
‫‪V   rddrdz‬‬
‫‪V‬‬
‫חשב נפח הגוף החסום‬
‫עיי' משטחים הבאים‬
‫)בתוך פרבלואים(‬
‫‪2‬‬
‫‪x  y  z  4a‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪x 2  y 2  3az‬‬
‫נחשב את הנפח הגוף בעזרת המעבר לקאורדינאטות גליליות‪,‬‬
‫ברור כי משטחים מוגדרים ע''י נוסחאות הבאות‬
‫‪2‬‬
‫‪3‬‬
‫‪az‬‬
‫‪‬‬
‫‪r‬‬
‫‪r  z  4a ,‬‬
‫אם נציב ‪ z  a‬באחת מהמשוואות נקבל ‪r  a 3.‬‬
‫‪2‬‬
‫‪4 a 2 r 2‬‬
‫‪rddr ‬‬
‫‪r2‬‬
‫‪3a‬‬
‫‪2‬‬
‫‪2‬‬
‫‪4 a r‬‬
‫‪ dz   z‬‬
‫‪D‬‬
‫‪2‬‬
‫‪2‬‬
‫‪2‬‬
‫‪r‬‬
‫‪3a‬‬
‫‪V  rddrdz   rddr‬‬
‫‪D‬‬
‫‪V‬‬
2
2
 2 2 r 

r 
2
2
  4a r  rddr d  r 4a r  dr
3a 
3a 
D
0 
0
2
a 3
a 3 3
 1a 3

r
2
2
2
2
 2    4a  r d 4a  r  
dr  
 2

3
a
0
0




‫המשך הפתרון‬
a 3
3
3
 2 2 2 3 2 r 


2
2
  a2 2  4a2 2 
  4a r 2 


3
4
3
3
3
a

0


4

a 3   2 16


a
4
3  4a
3
3
 
 
2 3 3 3 19 3

a 
a  a .
3
2
6
25
‫מצאו את נפח הגוף במרחב‬
‫המוגבל ע"י המשטחים‬
‫הנתונים ע"י המשטחים‬
:‫הבאים‬
z  x2  y2
z  8  x2  y2
:‫תשובה‬
I   dV   2

 0

2
x  y 4 z  x  y
D
  2
2
z 8  x 2  y 2
  2 z 8   2
 
0 z   2
2
dz dx dy
dz  d d
26
‫נתון תחום ‪ D‬סגור וחסום במרחב התלת‪-‬מימדי‪ .‬בעצם ‪D‬‬
‫מגדיר גוף שבו צפיפות החומר בנקודה )‪ (x,y,z‬מסומנת ב‪-‬‬
‫)‪.δ(x,y,z‬‬
‫המסה של הגוף‪:‬‬
‫‪M    ( x, y, z ) dV‬‬
‫‪D‬‬
‫מומנטים ראשונים‪:‬‬
‫קואורדינטות של מרכז הכובד‪:‬‬
‫‪M xy   z  ( x, y, z ) dV , M yz   x  ( x, y, z ) dV , M zx   y  ( x, y, z ) dV‬‬
‫‪D‬‬
‫‪D‬‬
‫‪D‬‬
‫‪M yz‬‬
‫‪M xy‬‬
‫‪M xz‬‬
‫‪x0 ‬‬
‫‪, y0‬‬
‫‪, z0 ‬‬
‫‪M‬‬
‫‪M‬‬
‫‪M‬‬
‫‪27‬‬
‫מצא את גבולות האינטגרציה‬
‫עבור פונקציה המוגדרת‬
‫בתחום ‪ D‬ב‪ R3 -‬המוגבל ע"י‬
‫מישור ‪xy‬‬
‫הגליל שמשוותו היא‬
‫‪x2+(y-1)2=1‬‬
‫הפרבולואיד שמשוואתו היא‬
‫‪z=x2+y2‬‬
‫‪28‬‬
:‫האינטגרל המבוקש‬
 
I 
 0

r  2 sin 
r 0

z r 2
z 0
f (r ,  , z ) dz r dr d
29
x  r cos  sin 
y  r sin  sin 
z  r cos 
dxdydz   2 sin  d d d
r x y z
2
2
2
30
‫( בתחום‬x,y,z) ‫ של שלושה משתנים‬f ‫נתונה פונקציה‬
:‫ אזי‬.R3 ‫ במרחב‬D ‫חסום וסגור‬

D
f ( x, y, z ) dV   f ( cos  sin  ,  sin  sin  ,  cos  )  2 sin  d d d
D
31
‫חישובי אינטגרלים משולשים בעזרת‬
‫קואורדינטות כדוריות‬
‫נפח כדור‬

D
f ( x, y, z ) dV   f ( cos  sin  ,  sin  sin  ,  cos  )  2 sin  d d d 
D

2
2
  d
0
R
 sin d  

0
2

 
 0
d 2 ( cos( ))


 3

3
 R

R3

 2  cos( )  cos(0) 

3
  0
2
4R 3

3
32
‫חישובי אינטגרלים משולשים בעזרת‬
‫קואורדינטות כדוריות‬
‫מצא את הנפח של הגוף המוגבל ע"י כדור שמרכזו בראשית‬
‫ורדיוסו ‪ ,2‬והחרוט שקודקודו בראשית וזווית הראשי ‪.  / 2‬‬
‫‪ 2 sin  d d d‬‬
‫‪33‬‬
‫‪ 2‬‬
‫‪0‬‬
‫‪‬‬
‫‪  / 4‬‬
‫‪0‬‬
‫‪‬‬
‫‪  2‬‬
‫‪V ‬‬
‫‪ 0‬‬