1. No category

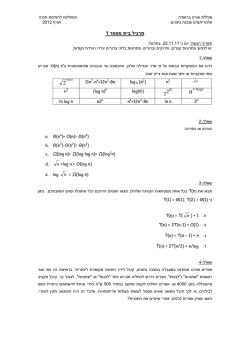
‫חוקי חזקות ולוגריתמים‬
‫חזקות‬
m
n
a ⋅a =a
m+n
3
2 ⋅2 =2
m
m n
m
3 5
n
x
3⋅5
a  =a =a
a⋅b =a ⋅b
m
 x=x
2
8
=2
4
2
m⋅n
m
8
12
a
m-n
=a
n
a
a  =a
5
m
m
m
15
2⋅3 =2 ⋅3
m
m
a
a
  = m
b
b
m
2
2
  = m
3
3
m
1
2
1
2
16 =  16=4
m
n
m
2
3
3
3
8 =  8 = 64=4
=x
1
a =a
2
0
a =1
1
am
m
−m
a
b
  = 
b
a
1 1
=
23 8
5
−5
2
3
  = 
3
2
−m
−3
a =
2 =
‫לוגריתמים‬
m
log a b=m ⇔ a =b
a0,a≠1 ‫ וגם‬b0
3
log 2 8=3 ⇔ 2 =8
‫תחום‬
: ‫הגדרה‬
log a b⋅c=log a blog a c
log 2 15=log 2 3⋅5=log 2 3log 2 5
b
log a  =log a b−log a c
c
6
log 10 3=log 10  =log6−log 2
2
(10 ‫ הכוונה היא לבסיס‬,‫ שימו לב שאם לא רשום בסיס‬: ‫)הערה‬
m
log a b =m⋅loga b
log a b
=log c b
log a c
log a 1=0 log a a=1
a
log a b
=b
2
log 7 25=log 7 5 =2⋅log 7 5
log 2 3
=log 5 3
log 2 5
log 8 1=0
2
log 2 5
log 8 8=1
=5