שאלון 805 - מתכונת מספר 1
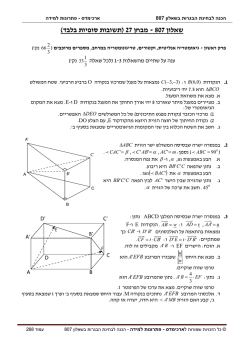
ארכימדס -פתרונות למידה הכנה לבחינת הבגרות בשאלון 805 שאלון - 805מתכונת מספר 1 1 3 פרק ראשון -סדרות וטריגונומטריה במרחב ) 33נק'( ענה על אחת מהשאלות מהשאלות 33 1 ) 1-2נק'( 3 .1הסדרה Anמוגדרת באמצעות כלל הנסיגה . a n +1 = (2 + a n ) ⋅ (n + 3) :באמצעות הסדרה Anמגדירים a n +1 = . bn סדרה חדשה Bnלפי הכלל: 2 + an א .הוכח ש Bn -היא סדרה חשבונית ומצא את הנוסחה לאיבר הכללי שלה. ב .בסדרה Bnבחרו שלושה איברים רצופים .למספר הראשון מביניהם הוסיפו 19ומהשלישי החסירו .7לאחר שינויים אלו ,התקבלו שלושה איברים ראשונים בהתאמה ,בסדרה הנדסית חדשה .מצא את מנת הסדרה ההנדסית החדשה. ג .הסדרה ההנדסית החדשה היא סדרה אינסופית .חשב בה את סכום האיברים הנמצאים במקומות הזוגיים. .2נתונה הפירמידה הישרה SABCDשבסיסה מלבן .אלכסוני המלבן נחתכים בנקודה .Oנסמן ,BC = 18 m ,AB = 24m :האורך של כל אחד ממקצועות הצד הוא .25m א .הבע באמצעות mאת גובה הפירמידה. ב .נתון :נפח הפירמידה 23,040סמ"ק .מצא את ערכו של הפרמטר .m ג .הנקודות Eו F-הן בהתאמה אמצעי המקצועות BCו.AB- חשב את שטח המשולש . ∆SEF 2 3 פרק שני -גדילה ודעיכה ,חד"וא של פונקציות טריגונומטריות ,מעריכיות ולוגריתמיות ) 66נק'( ענה על שתיים מהשאלות מהשאלות 33 1 ) 3-5נק' לכל שאלה( 3 .3נתון גרף הפונקציה f ( x) = 2 x − a ⋅ sin xבתחום . 0 ≤ x ≤ π א .הוכח שגרף הפונקציה ) f (xעובר דרך ראשית הצירים. ב .קבע האם הפונקציה ) f (xהיא זוגית ,אי זוגית או שאינה זוגית ואינה אי זוגית .נמק. π ג .נתון :בתחום 0 ≤ x ≤ πגרף הנגזרת ) f ' ( xחותך את ציר ה x-רק בנקודה בה = . x 3 מצא את ערכו של הפרמטר .a ד .נתון ישר המשיק לגרף הפונקציה ) f (xבראשית הצירים .דרך נקודת המינימום המופיעה בשרטוט עובר ישר נוסף המקביל לציר ה .y-חשב את השטח הכלוא בין שני הישרים לבין גרף הפונקציה. © כל הזכויות שמורות לארכימדס -פתרונות למידה -הכנה לבחינת הבגרות בשאלון 805 מותר לצלם לשימוש פנימי במשך שנת הלימודים תשע"ד בלבד בציון המקור ארכימדס -פתרונות למידה הכנה לבחינת הבגרות בשאלון 805 .4נקודת הקיצון היחידה של הפונקציה f ( x) = 2e x +1 − e 2 x + m :נמצאת על הישר . y = e 2 א .עבור גרף הפונקציה ) f (xמצא את: (1ערכו של הפרמטר .m (2נקודות החיתוך עם הצירים. (3נקודת הקיצון ואת סוגה. ב .שרטט את גרף הפונקציה ) f (xברביע הראשון בלבד. ג .דרך נקודת הקיצון של גרף הפונקציה ) f (xמעבירים משיק לגרף הפונקציה .חשב את השטח הכלוא בין גרף הפונקציה לבין המשיק וציר ה.y- .5הוריו של דניאל נסעו לאיטליה והפקידו בידיו את הטיפול בגינה .דניאל התרשל ולא השקה את העציץ האהוב על אימו .בחמשת הימים הראשונים הידלדלה כמות העלים בעציץ באחוז קבוע בכל יום .לאחר חמשת הימים הללו היתה כמות העלים בעציץ נמוכה ב 40%-מכמותה ביום שבו נסעו ההורים. א .מצאו מה הוא האחוז הקבוע שבו ירדה כמות העלים בכל יום. ב .לאחר חמישה ימים אלו התעשת דניאל והחל להשקות את העציץ האהוב על אימו .מרגע זה גדלה מדי יום כמות העלים באחוז הגדול פי 1.2מאחוז הנשירה של העלים כאשר לא השקה אותם .חשב כמה ימים נוספים יחלפו מרגע שהחל להשקות את העציץ עד אשר תחזור כמות העלים על העציץ לכמות המקורית ביום בו טסו הוריו. בהצלחה! פתרונות: 1 (1א . bn = n + 3 .ב. 3 (2א .20m .ב . m = 2 .ג 637.688 .סמ"ר. = . qג.10.125 . (3ב .אי זוגית .ג . a = 4 .ד 0.193 .יח"ר. (4א( . (1.69, 0) , (0, 4.437) (2 . m = 0 (1 ב( השרטוט משמאל .ג( 1.242יח"ר. 2 . max(1, e ) (3 (5א .9.71% .ב 4.63 .ימים. © כל הזכויות שמורות לארכימדס -פתרונות למידה -הכנה לבחינת הבגרות בשאלון 805 מותר לצלם לשימוש פנימי במשך שנת הלימודים תשע"ד בלבד בציון המקור
© Copyright 2026