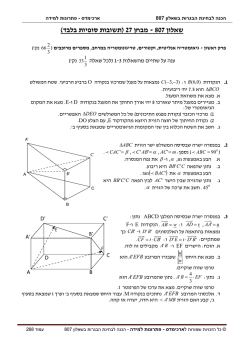
‫ארכימדס ‪ -‬פתרונות למידה‬ ‫הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫שאלון ‪ - 806‬מבחן ‪26‬‬ ‫‪1‬‬ ‫‪3‬‬ ‫פרק ראשון ‪ -‬אלגברה והסתברות ) ‪ 33‬נק'(‬ ‫‪2‬‬ ‫ענה על שתיים מהשאלות ‪) 1-3‬לכל שאלה‬ ‫‪3‬‬ ‫‪ 16‬נק'(‬ ‫‪ .1‬בו זמנית‪ ,‬יוצאים קטנוע מהנקודה ‪ A‬לנקודה ‪ ,B‬ומכונית מהנקודה ‪B‬‬ ‫לנקודה ‪) C‬בהתאם לשרטוט(‪ .‬כעבור שעה‪ ,‬יוצא רוכב אופניים מהנקודה ‪ A‬לנקודה ‪ .C‬השלושה הגיעו‬ ‫ליעדם באותו רגע‪ .‬מהירות הקטנוע כפולה ממהירות האופניים ואורך הקטע ‪ BC‬הוא ‪ 100‬ק"מ‪.‬‬ ‫כשהגיעה המכונית למחצית הדרך בין הנקודה ‪ A‬לנקודה ‪ ,B‬היה המרחק בינה לבין הקטנוע ‪ 8‬ק"מ והם‬ ‫טרם חלפו זה על פני זו‪.‬‬ ‫א‪ .‬חשב את מהירויות המכונית‪ ,‬הקטנוע ורוכב האופניים‪.‬‬ ‫ב‪ .‬למחרת‪ ,‬כאשר יצאו מאותן נקודות לאותם יעדים באותה שעה כמו בתיאור הקודם‪ ,‬מהירות‬ ‫האופניים פחתה ב‪ v-‬קמ"ש ומהירות הקטנוע גדלה ב‪ v-‬קמ"ש‪ .‬כאשר הקטנוע הגיע לנקודה ‪ ,B‬מרחק‬ ‫האופניים מהנקודה ‪ C‬היה ‪ 14‬ק"מ‪ .‬מצא את ערכו של הפרמטר ‪.v‬‬ ‫‪ .2‬בסדרה הנדסית עולה שאיבריה חיוביים‪ ,‬מכפלת האיברים השני‪ ,‬השלישי והרביעי היא ‪ .729‬מחסרים‬ ‫מהאיבר השני ‪ 2‬ומגדילים את האיבר הרביעי פי שלושה‪ .‬את האיבר השלישי לא משנים‪ .‬לאחר השינויים‪,‬‬ ‫מהווים שלושת האיברים סדרה הנדסית חדשה‪.‬‬ ‫א‪ .‬מצא את המנה של הסדרה המקורית לפני השינויים‪.‬‬ ‫ב‪ .‬בסדרה המקורית יש מספר זוגי של איברים‪ .‬מכפילים פי ‪ k‬את האיברים הנמצאים במקומות הזוגיים‬ ‫ומחלקים ב‪ k-‬את האיברים הנמצאים במקומות האי זוגיים‪ .‬מצא עבור אילו ערכי ‪ ,k‬סכום הסדרה‬ ‫אחרי שני שינויים אלו‪ ,‬קטן מסכום הסדרה המקורית‪.‬‬ ‫‪ .3‬ביום שבו הגיעו המתיישבים למאדים רק ‪ 30%‬מהם רכשו בכספם דירה‪ .‬מי שלא יכול היה לרכוש דירה‪,‬‬ ‫ניגש באותו יום להגרלה‪ ,‬בה היתה הסתברות של ‪ 0.4‬לזכות בדירה‪ .‬מי שהשתתף בהגרלה אך לא זכה‬ ‫בדירה‪ ,‬הגיש באותו יום בקשה מיוחדת לקבלת דירה‪ .‬רק שליש ממגישי בקשה זו קיבלו דירה‪.‬‬ ‫א‪ .‬יונתן הגיע למאדים באותו יום‪ .‬חשב את ההסתברות שבאותו לילה‪ ,‬היתה לו דירה‪.‬‬ ‫ב‪ .‬למחרת יום ההתיישבות‪ ,‬נמצא ש‪ 32%-‬מהמתיישבים היו בעלי דירה עם חניה‪.‬‬ ‫נסמן שני מאורעות‪ :‬המאורע ‪ A‬הוא‪" :‬להיות בעל דירה"‪ .‬המאורע ‪ B‬הוא‪" :‬להיות בעל חניה"‪.‬‬ ‫‪ (1‬קבע באיזה תחום מספרים נמצאת ההסתברות ) ‪. P(B‬‬ ‫‪ (2‬קבע באיזה תחום מספרים נמצאת ההסתברות ) ‪. P (B‬‬ ‫‪ (3‬חשב את סכום ההסתברויות‪. P B + P A I B :‬‬ ‫ג‪ .‬ידוע שההסתברות לבחור במאדים בעל דירה שאין לו חניה‪ ,‬גדולה פי שניים מההסתברות לבחור‬ ‫במאדים בעל חניה שאין לו דירה‪ .‬חשב את ההסתברות לבחור במאדים אדם ללא דירה ולא חניה‪.‬‬ ‫)‬ ‫( )(‬ ‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫עמוד ‪212‬‬ ‫הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫ארכימדס ‪ -‬פתרונות למידה‬ ‫‪1‬‬ ‫‪3‬‬ ‫פרק שני ‪ -‬גיאומטריה וטריגונומטריה במישור ) ‪ 33‬נק'(‬ ‫‪2‬‬ ‫ענה על שתיים מהשאלות ‪) 4-6‬לכל שאלה‬ ‫‪3‬‬ ‫‪ 16‬נק'(‬ ‫‪ .4‬בשרטוט מופיעים הריבועים ‪ ABCD‬ו‪ .EFGH-‬הנקודות ‪ F ,D‬ו‪M-‬‬ ‫נמצאות על אותו ישר‪ .‬הנקודות ‪ G ,C‬ו‪ M-‬נמצאות על אותו ישר‪.‬‬ ‫א‪ .‬הוכח‪. ME ⋅ BH = AE ⋅ MH :‬‬ ‫ב‪ .‬נתון‪ :‬שטחי המשולשים ‪ ∆ MEF‬ו‪ ∆MHG -‬הם בהתאמה‬ ‫‪ 24‬סמ"ר ו‪ 8-‬סמ"ר‪ .‬שטח הטרפז ‪ CDFG‬הוא ‪ 168‬סמ"ר‪.‬‬ ‫חשב את שטח הטרפז ‪.BCGH‬‬ ‫ג‪ .‬חשב את היקף הטרפז ‪.ADFE‬‬ ‫‪ .5‬במעגל שמרכזו בנקודה ‪ O‬ושטחו ‪ 169π‬סמ"ר‪ ,‬המיתר ‪ EF‬חוסם‬ ‫את המלבן ‪ ABCD‬ששטחו ‪ 70‬סמ"ר‪ .‬המרחק בין מרכז המעגל‬ ‫לבין המיתר ‪ EF‬קטן פי שניים מאורך ‪ .AB‬אורכי צלעות המלבן‬ ‫הם מספרים שלמים‪.‬‬ ‫א‪ .‬חשב את שטח המשולש ‪. ∆ CEO‬‬ ‫ב‪ .‬מעבירים את המיתר ‪ .BE‬חשב את המרחק בין הנקודה ‪ O‬לבין‬ ‫מרכזו של מעגל אחר‪ ,‬שקוטרו ‪.BE‬‬ ‫ג‪ .‬הנקודה ‪ M‬נמצאת על הקשת ‪ EF‬בצד התחתון של הציור‪.‬‬ ‫חשב את הזוית ‪. p BME‬‬ ‫‪ .6‬במשולש ‪ ∆ABC‬נתון‪. AB + AC = 7a , p ACB = β , p ABC = α :‬‬ ‫א‪ .‬נתון‪ . 3 sin β = 4 sin α :‬הבע באמצעות ‪ a‬את אורכי הצלעות ‪ AB‬ו‪.AC-‬‬ ‫) ‪cos α 3 ⋅ (b 2 + 7a 2‬‬ ‫ב‪ .‬נסמן‪ .BC = b :‬הוכח‪:‬‬ ‫‪.‬‬ ‫=‬ ‫) ‪cos β 4 ⋅ (b 2 − 7a 2‬‬ ‫ג‪ .‬נתון‪ . 4 cos β = 3 cos α :‬חשב את גודל הזוית ‪. p BAC‬‬ ‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫עמוד ‪213‬‬ ‫ארכימדס ‪ -‬פתרונות למידה‬ ‫הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫פרק שלישי ‪ -‬חשבון דיפרנציאלי ואינטגרלי של פולינומים‪ ,‬פונקציות שורש‪ ,‬פונקציות רציונליות‬ ‫‪1‬‬ ‫‪3‬‬ ‫ופונקציות טריגונומטריות ) ‪ 33‬נק'(‬ ‫‪2‬‬ ‫ענה על שתיים מהשאלות ‪) 7-9‬לכל שאלה‬ ‫‪3‬‬ ‫‪2‬‬ ‫‪a‬‬ ‫‪ .7‬נתונה הנגזרת השניה‪+ 5 :‬‬ ‫‪3‬‬ ‫‪x‬‬ ‫‪x‬‬ ‫‪ 16‬נק'(‬ ‫‪ . f ' ' ( x) = −‬הישר ‪ x = 2‬חותך את גרף הפונקציה ) ‪ f (x‬בנקודת הפיתול‬ ‫‪2‬‬ ‫שלה ברביע הראשון‪ .‬שיפוע המשיק לגרף הפונקציה ) ‪ f (x‬בנקודה בה ‪ x = 0.5‬הוא ‪ .-27‬הישר‬ ‫‪3‬‬ ‫משיק לגרף הפונקציה ) ‪ f (x‬ברביע הראשון‪.‬‬ ‫א‪.‬‬ ‫ב‪.‬‬ ‫ג‪.‬‬ ‫ד‪.‬‬ ‫ה‪.‬‬ ‫=‪y‬‬ ‫מצא את הפונקציה ) ‪. f (x‬‬ ‫שרטט את גרף הפונקציה ) ‪ f (x‬בתחום ‪. 0 ≤ x‬‬ ‫קבע האם הפונקציה ) ‪ f (x‬זוגית או אי זוגית‪ ,‬ושרטט בהתאם את הגרף המלא שלה‪.‬‬ ‫שרטט את גרף הנגזרת ) ‪. f ' ( x‬‬ ‫דרך נקודת הקיצון של גרף הנגזרת ) ‪ f ' ( x‬ברביע הראשון מורידים אנך לציר ה‪ .x-‬חשב את השטח‬ ‫הכלוא בין אנך זה‪ ,‬לבין הישר ‪ x = 3‬לבין גרף הנגזרת ) ‪ f ' ( x‬והאסימפטוטה האופקית של הגרף‪.‬‬ ‫)הנח שאין בתחום הכלוא נקודות קיצון נוספות או נקודות פיתול נוספות(‪.‬‬ ‫‪2 + 2 tan x‬‬ ‫‪ .8‬נתונה הנגזרת‪:‬‬ ‫‪cos 2 x‬‬ ‫= )‪ . f ' ( x‬מבין אינסוף נקודות הקיצון של גרף הפונקציה )‪ , f (x‬נקודת‬ ‫הקיצון הקרובה ביותר לציר ה‪ ,y-‬נמצאת על הישר ‪. y = 1‬‬ ‫א‪ .‬מצא את משוואת הפונקציה )‪. f (x‬‬ ‫ב‪ .‬בתחום‪ 0 ≤ x ≤ π :‬מצא את‪:‬‬ ‫‪ .1‬האסימפטוטות לגרף הפונקציה‪.‬‬ ‫‪ .2‬נקודות הקיצון של הפונקציה ואת סוגן‪.‬‬ ‫‪ .3‬נקודות החיתוך עם הצירים‪.‬‬ ‫‪ .4‬תחומי העליה והירידה של גרף הפונקציה‪.‬‬ ‫ג‪ .‬שרטט סקיצה של גרף הפונקציה )‪ f (x‬בתחום הנתון‪.‬‬ ‫ד‪ .‬מצא את שיפועי הישרים המשיקים לגרף הפונקציה בקצות התחום הנתון‪.‬‬ ‫ה‪ .‬נתון שגרף הפונקציה )‪ f (x‬חותך את גרף הנגזרת ) ‪ f ' ( x‬בנקודה אחת בתחום‪ . 0 < x < π :‬מצא כמה‬ ‫פתרונות יש למשוואה )‪ f ( x) = f ' ( x‬בתחום הנתון‪ .‬נמק‪.‬‬ ‫‪ .9‬הפירמידה ‪ SABCD‬היא ישרה ובסיסה ריבוע‪.‬‬ ‫היקפו של המשולש ‪ ∆ASC‬הוא שישה ס"מ‪.‬‬ ‫נסמן‪.BD = 2x :‬‬ ‫חשב את הנפח המקסימלי של הפירמידה‪.‬‬ ‫בהצלחה!‬ ‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫עמוד ‪214‬‬ ‫ארכימדס ‪ -‬פתרונות למידה‬ ‫הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫פתרונות‪:‬‬ ‫‪ (1‬א‪ .‬קטנוע‪ 40 :‬קמ"ש‪ ,‬אופניים‪ 20 :‬קמ"ש‪ ,‬מכונית‪ 50 :‬קמ"ש‪ .‬ב‪ 10 .‬קמ"ש‪.‬‬ ‫‪1‬‬ ‫‪ (2‬א‪ . q = 3 .‬ב‪< k < 1 .‬‬ ‫‪3‬‬ ‫‪ (3‬א‪ .0.72 .‬ב‪ .0.68 (3 . 0.4 ≤ P B ≤ 0.68 (2 . 0.32 ≤ P(B ) ≤ 0.6 (1 .‬ג‪.0.08 .‬‬ ‫או ‪. k < 0‬‬ ‫)(‬ ‫‪ (4‬ב‪ 42 .‬סמ"ר‪ .‬ג‪ 52 .‬ס"מ‪.‬‬ ‫‪ (5‬א‪ 17.5 .‬סמ"ר‪ .‬ב‪ 12.02 .‬ס"מ‪ .‬ג‪. 22.38 .‬‬ ‫‪ (6‬א‪ . AB = 4a, AC = 3a .‬ג‪. p BAC = 90 0 .‬‬ ‫‪0‬‬ ‫‪2‬‬ ‫‪ (7‬א‪+ x .‬‬ ‫‪3x 3‬‬ ‫‪1‬‬ ‫‪x‬‬ ‫‪ . f ( x) = − +‬ב‪.‬‬ ‫ד‪.‬‬ ‫ג‪ .‬אי זוגית‪ .‬השרטוט‪:‬‬ ‫ה‪ 0.108 .‬יח"ר‪.‬‬ ‫‪1‬‬ ‫‪ (8‬א‪ . f ( x) = tan 2 x + 2 tan x + 2 .‬ניתן גם להגיע לפונקציה השקולה‪+ 2 tan x + 1 :‬‬ ‫‪2‬‬ ‫‪cos x‬‬ ‫‪3π‬‬ ‫ב‪. (0,2) (3 . min(0,2) , min( ,1) , max(π ,2) (2 . x = π (1 .‬‬ ‫‪4‬‬ ‫‪2‬‬ ‫‪π‬‬ ‫‪3π‬‬ ‫‪π‬‬ ‫‪3π‬‬ ‫ג‪.‬‬ ‫<‪. <x‬‬ ‫או < ‪ . 0 < x‬ירידה‪:‬‬ ‫‪ (4‬עליה‪< x < π :‬‬ ‫‪2‬‬ ‫‪4‬‬ ‫‪2‬‬ ‫‪4‬‬ ‫ד‪ .‬בשניהם השיפוע ‪.2‬‬ ‫= )‪. f ( x‬‬ ‫ה‪ .‬שלושה פתרונות‪.‬‬ ‫‪ (9‬הנפח‪ 1.288 :‬סמ"ק‪.‬‬ ‫© כל הזכויות שמורות לארכימדס ‪ -‬פתרונות למידה ‪ -‬הכנה לבחינת הבגרות בשאלון ‪806‬‬ ‫עמוד ‪215‬‬