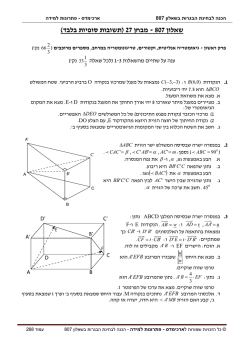
‫בגרות לבתי ספר על־יסודיים‬ ‫סוג הבחינה‪:‬‬ ‫‬ ‫מועד הבחינה‪ :‬חורף תשע"ד‪2014 ,‬‬ ‫מספר השאלון‪035004 :‬‬ ‫‬ ‫מדינת ישראל‬ ‫משרד החינוך‬ ‫‬ ‫הצעת תשובות לשאלות בחינת הבגרות‬ ‫מתמטיקה‬ ‫שאלון ד'‬ ‫הוראות לנבחן‬ ‫א‪.‬‬ ‫משך הבחינה‪ :‬שעה ושלושה רבעים‪.‬‬ ‫ב‪.‬‬ ‫מבנה השאלון ומפתח ההערכה‪ :‬בשאלון זה שני פרקים‪.‬‬ ‫פרק ראשון‬ ‫‬ ‫טריגונומטריה במישור ובמרחב‪,‬‬ ‫—‬ ‫‬ ‫חשבון דיפרנציאלי ואינטגרלי של‬ ‫‬ ‫הפונקציות הטריגונומטריות‬ ‫‬ ‫—‬ ‫פרק שני‬ ‫—‬ ‫—‬ ‫חשבון דיפרנציאלי ואינטגרלי‬ ‫‬ ‫‪1‬‬ ‫‪2‬‬ ‫‪33 3 #2‬‬ ‫—‬ ‫‪ 66 3‬נקודות‬ ‫סה"כ‬ ‫—‬ ‫‪ 100‬נקודות‬ ‫חומר עזר מותר בשימוש‪:‬‬ ‫(‪)1‬‬ ‫‬ ‫מחשבון לא גרפי‪ .‬אין להשתמש באפשרויות התכנות במחשבון הניתן לתכנות‪.‬‬ ‫שימוש במחשבון גרפי או באפשרויות התכנות במחשבון עלול לגרום לפסילת הבחינה‪.‬‬ ‫(‪)2‬‬ ‫ד‪.‬‬ ‫‪33 3 #1‬‬ ‫—‬ ‫‪ 33 3‬נקודות‬ ‫חזקות ולוגריתמים‪,‬‬ ‫‬ ‫ג‪.‬‬ ‫‪1‬‬ ‫‪1‬‬ ‫דפי נוסחאות (מצורפים)‪.‬‬ ‫הוראות מיוחדות‪:‬‬ ‫(‪)1‬‬ ‫אל תעתיק את השאלה; סמן את מספרה בלבד‪.‬‬ ‫(‪)2‬‬ ‫התחל כל שאלה בעמוד חדש‪ .‬רשום במחברת את שלבי הפתרון‪ ,‬גם כאשר‬ ‫‬ ‫החישובים מתבצעים בעזרת מחשבון‪.‬‬ ‫‬ ‫הסבר את כל פעולותיך‪ ,‬כולל חישובים‪ ,‬בפירוט ובצורה ברורה ומסודרת‪.‬‬ ‫‬ ‫חוסר פירוט עלול לגרום לפגיעה בציון או לפסילת הבחינה‪.‬‬ ‫(‪)3‬‬ ‫לטיוטה יש להשתמש במחברת הבחינה או בדפים שקיבלת מהמשגיחים‪.‬‬ ‫‬ ‫שימוש בטיוטה אחרת עלול לגרום לפסילת הבחינה‪.‬‬ ‫ההנחיות בשאלון זה מנוסחות בלשון זכר ומכוונות לנבחנות ולנבחנים כאחד‪.‬‬ ‫בהצלחה!‬ ‫‪/‬המשך מעבר לדף‪/‬‬ ‫(‪ )2‬סכום שלושת האיברים שבתת־סעיף ב(‪ )1‬הוא ‪. 133‬‬ ‫מצא את הפרש הסדרה החשבונית הנתונה‪.‬‬ ‫(‪ )3‬סכום ‪ n‬האיברים הראשונים בסדרה הנתונה מקיים ‪. S n 211, 977‬‬ ‫‪2‬‬‫אי־שוויון‪ -‬זה‪.‬‬ ‫מצא את ‪ n‬הקטן ביותר המקיים‬ ‫שאלה ‪1‬‬ ‫טריגונומטריה במרחב‬ ‫‪ .2‬נתונה פירמידה ישרה ‪ SABCD‬שבסיסה ריבוע‬ ‫וגובהה ‪. SO‬‬ ‫הנקודה ‪ E‬היא אמצע הצלע ‪( BC‬ראה ציור)‪.‬‬ ‫הזווית בין ‪ SE‬לבסיס הפירמידה היא ‪. 75o‬‬ ‫אורך צלע הבסיס הוא ‪. a‬‬ ‫א‪ )1( .‬הבע באמצעות ‪ a‬את האורך של ‪. SE‬‬ ‫(‪ )2‬הבע באמצעות ‪ a‬את שטח המעטפת‬ ‫‪B‬‬ ‫של הפירמידה ‪. SABCD‬‬ ‫‪1‬‬ ‫ב‪ .‬הנקודה ‪ F‬נמצאת על הגובה ‪ SO‬כך ש־ ‪. FO = 3 SO‬‬ ‫בפירמידה הישרה ‪ FABCD‬חשב את הזווית‬ ‫בין מקצוע צדדי לבסיס‪.‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪S‬‬ ‫‪F‬‬ ‫‪A‬‬ ‫‪O‬‬ ‫‪E‬‬ ‫‪D‬‬ ‫‪C‬‬ ‫‪/‬המשך בעמוד ‪/3‬‬ ‫תשובה לשאלה ‪1‬‬ ‫א‪.‬‬ ‫‬ ‫‪B SEO = 75 o‬‬ ‫(‪ )1‬לפי ההגדרה של זווית בין ישר למישור נקבל‪:‬‬ ‫במשולש ישר־הזווית ‪ SOE‬מתקיים‪:‬‬ ‫‪OE‬‬ ‫‪cos (B SEO) = SE‬‬ ‫‪0‬‬ ‫‬ ‫‪a‬‬ ‫‪2‬‬ ‫‪o‬‬ ‫‪cos 75 = SE‬‬ ‫‬ ‫‪0‬‬ ‫‬ ‫‬ ‫‬ ‫(‪ )2‬שטח המעטפת הוא‪:‬‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫‪SE = 1.93a‬‬ ‫‪ = 4 $ S3SBC‬שטח מעטפת‬ ‫‪1‬‬ ‫‪1‬‬ ‫‪S3SBC = 2 $ SE $ BC = 2 $1.93a $ a‬‬ ‫‪0‬‬ ‫‪1‬‬ ‫‪ = 4 $ 2 $1.93a $ a‬שטח מעטפת‬ ‫‪0‬‬ ‫‪3.86a2‬‬ ‫= שטח מעטפת‬ ‫‪/‬המשך בעמוד ‪/3‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪-3‬‬‫המשך תשובה לשאלה ‪.1‬‬ ‫ב‪.‬‬ ‫לפי ההגדרה של זווית בין ישר למישור‬ ‫נקבל כי הזווית המבוקשת היא למשל‪:‬‬ ‫‪B FBO‬‬ ‫‬ ‫במשולש ישר־הזווית ‪ FOB‬מתקיים‪:‬‬ ‫‪FO‬‬ ‫‪tg BFBO = BO‬‬ ‫‬ ‫במשולש ‪ SOE‬מתקיים‪:‬‬ ‫‬ ‫‪SO‬‬ ‫)‪EO = tg (BSEO‬‬ ‫‪0‬‬ ‫‬ ‫‬ ‫‬ ‫‪a‬‬ ‫‪SO = 2 $ tg75 o‬‬ ‫‪1‬‬ ‫‪FO = 3 SO‬‬ ‫לפי הנתון‪:‬‬ ‫‪0‬‬ ‫‬ ‫‪a tg75 o‬‬ ‫‪FO = 6‬‬ ‫‬ ‫‪1‬‬ ‫‬ ‫‪ BO‬הוא ‪ 2‬אלכסון הבסיס‪ ,‬לכן‪:‬‬ ‫‬ ‫מהצבת ‪ FO‬ו־ ‪ BO‬נקבל‪:‬‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫‪2a‬‬ ‫‪BO = 2‬‬ ‫‪a tg75 o‬‬ ‫‪6‬‬ ‫= )‪tg (BFBO‬‬ ‫‪2a‬‬ ‫‪2‬‬ ‫‪0‬‬ ‫‪2 tg75 o‬‬ ‫‪6‬‬ ‫= )‪tg (BFBO‬‬ ‫‪0‬‬ ‫‪BFBO = 41.3 o‬‬ ‫‬ ‫‪/‬המשך בעמוד ‪/4‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪-4-‬‬ ‫תשע"ד‪ ,‬מס' ‪ + 315 ,035805‬נספח‬ ‫מתמטיקה‪ ,‬חורף‬ ‫שאלה ‪2‬‬ ‫‪-4-‬‬ ‫‪5r‬‬ ‫‪.4‬‬ ‫נתונה הפונקציה ‪ f (x) = - 2 cos (2x) + a‬בתחום ‪. 0 # x # 6‬‬ ‫‪ a‬הוא פרמטר המקיים ‪. 0 1 a 1 2‬‬ ‫מצא את השיעורים של נקודות המקסימום המוחלט והמינימום המוחלט של הפונקציה )‪f(x‬‬ ‫א‪.‬‬ ‫(הבע באמצעות ‪ a‬במידת הצורך)‪.‬‬ ‫נתון כי הישר ‪ y = 3‬משיק לגרף הפונקציה )‪ f(x‬בתחום הנתון‪.‬‬ ‫ב‪.‬‬ ‫מצא את הערך של ‪. a‬‬ ‫הצב ‪ , a = 1‬וענה על הסעיפים ג ו־ ד‪.‬‬ ‫ג‪.‬‬ ‫בתחום הנתון סרטט סקיצה של גרף הפונקציה )‪. f(x‬‬ ‫ד‪.‬‬ ‫בתחום הנתון מצא את השטח המוגבל על ידי גרף הפונקציה )‪ , f(x‬על ידי המשיק ‪y = 3‬‬ ‫ועל ידי ציר ה־ ‪. y‬‬ ‫‬ ‫נתונה הפונקציה ‪ a , f (x) = (a - 3x) e3x‬הוא פרמטר‪.‬‬ ‫תשובה לשאלה ‪2‬‬ ‫‪.5‬‬ ‫א‪.‬‬ ‫א‪.‬‬ ‫ב‪.‬‬ ‫מהו תחום ההגדרה של הפונקציה?‬ ‫)‪f' (x) = 4 sin (2x‬‬ ‫הנגזרת של )‪: f(x‬‬ ‫ידוע כי שיעור ה־ ‪ x‬של נקודת הקיצון של הפונקציה )‪ f(x‬הוא ‪. 1‬‬ ‫מצא את הערך של ‪. a‬‬ ‫‪sin (2x) = 0‬‬ ‫‬ ‫ וענה על הסעיפים ג ו־ ד‪.‬‬ ‫הצב ‪, a = 4‬‬ ‫ ג‪.‬‬ ‫&‬ ‫‪f' (x) = 0‬‬ ‫‪0‬‬ ‫‪r‬‬ ‫‪r‬‬ ‫)‪. f(x‬‬ ‫מצא‪5‬את‬ ‫(‪)1‬‬ ‫‪#x#‬‬ ‫=‪x‬‬ ‫הפונקציה ‪0 ,‬‬ ‫תחומי‪: 0‬העלייה והירידה של = ‪x‬‬ ‫בתחום‬ ‫‪2‬‬ ‫‪6‬‬ ‫(‪ )2‬מצא את נקודות החיתוך של גרף הפונקציה )‪ f(x‬עם הצירים‪.‬‬ ‫ (‪ )3‬סרטט סקיצה של גרף הפונקציה )‪. f(x‬‬ ‫נתון הישר ‪. k # 0 , y = k‬‬ ‫ד‪.‬‬ ‫‪5r‬‬ ‫‪6‬‬ ‫‪a -1‬‬ ‫‪r‬‬ ‫‪2‬‬ ‫‪a+2‬‬ ‫‪0‬‬ ‫‪x‬‬ ‫‪a-2‬‬ ‫)‪f(x‬‬ ‫לישר זה עם גרף הפונקציה )‪ ? f(x‬נמק‪.‬‬ ‫כמה נקודות חיתוך יש‬ ‫‬ ‫‪3‬‬ ‫‪4‬‬ ‫‪a - 2 1 a - 11 a + 2‬‬ ‫‬ ‫‬ ‫בהצלחה!‬ ‫‪0‬‬ ‫זכות היוצרים שמורה למדינת ישראל‬ ‫החינוך‪a +‬‬ ‫ברשות משרד ‪2 k‬‬ ‫בנקודה‪:‬‬ ‫מוחלט‬ ‫מקסימום‬ ‫יש‬ ‫לפרסם אלא‬ ‫להעתיק או‬ ‫אין‬ ‫‬ ‫לפונקציה )‪f(x‬‬ ‫‬ ‫לפונקציה )‪ f(x‬יש מינימום מוחלט בנקודה‪:‬‬ ‫‪r‬‬ ‫‪a2 ,‬‬ ‫‪^ 0 , a - 2h‬‬ ‫‪/‬המשך בעמוד ‪/5‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪-5‬‬‫המשך תשובה לשאלה ‪.2‬‬ ‫ב‪.‬‬ ‫‬ ‫שיפוע הישר ‪ y = 3‬הוא ‪, 0‬‬ ‫‪f' (x) = 0‬‬ ‫כלומר הוא משיק לפונקציה בנקודה שבה‪:‬‬ ‫‬ ‫‪0‬‬ ‫‪r‬‬ ‫‪x= 2‬‬ ‫‪ y = 3‬בנקודה שבה‪:‬‬ ‫‬ ‫‬ ‫‪0‬‬ ‫‪r‬‬ ‫‪fa 2 k = 3‬‬ ‫‬ ‫‬ ‫‪0‬‬ ‫מצאנו כי ‪ , f a 2 k = a + 2‬לכן‪:‬‬ ‫‪r‬‬ ‫‬ ‫‪a+2=3‬‬ ‫‬ ‫‪0‬‬ ‫‪a =1‬‬ ‫‬ ‫ג‪.‬‬ ‫‪y‬‬ ‫‪3‬‬ ‫‪x‬‬ ‫‬ ‫ד‪.‬‬ ‫‪5r‬‬ ‫‪6‬‬ ‫‪-1‬‬ ‫‪r‬‬ ‫‪2‬‬ ‫השטח המבוקש הוא השטח המקווקו בציור‪:‬‬ ‫‪y‬‬ ‫‪3‬‬ ‫‬ ‫‪x‬‬ ‫‪r‬‬ ‫‪2‬‬ ‫‬ ‫‬ ‫‬ ‫‪0‬‬ ‫‪(2 + 2 cos (2x)) dx‬‬ ‫‪r‬‬ ‫‪2‬‬ ‫‪#‬‬ ‫‪0‬‬ ‫= ‪(3 - f (x)) dx‬‬ ‫‬ ‫‬ ‫‪-1‬‬ ‫‪r‬‬ ‫‪2‬‬ ‫‪#‬‬ ‫‪0‬‬ ‫=‪S‬‬ ‫‪0‬‬ ‫‪S=r‬‬ ‫‪r‬‬ ‫&‬ ‫‪S = 62x + sin (2x)@ 2‬‬ ‫‪0‬‬ ‫‪/‬המשך בעמוד ‪/6‬‬ ‫‪2‬‬ ‫( ‪ 66 3‬נקודות)‬ ‫‪1‬‬ ‫ענה על שתיים מהשאלות ‪( 5-3‬לכל שאלה — ‪ 33 3‬נקודות)‪.‬‬ ‫‪-6‬‬‫שים לב! אם תענה על יותר משתי שאלות‪ ,‬ייבדקו רק שתי התשובות הראשונות שבמחברתך‪.‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫שאלה ‪3‬‬ ‫‪.3‬‬ ‫‪x2 - 5‬‬ ‫נתונה הפונקציה ‪. f (x) = x + 3‬‬ ‫א‪.‬‬ ‫(‪ )1‬מצא את תחום ההגדרה של הפונקציה‪.‬‬ ‫(‪ )2‬מצא את נקודות החיתוך של גרף הפונקציה עם הצירים‪.‬‬ ‫(‪ )3‬מצא את האסימפטוטות של הפונקציה המקבילות לצירים (אם יש כאלה)‪.‬‬ ‫(‪ )4‬מצא את השיעורים של נקודות הקיצון של הפונקציה‪ ,‬וקבע את סוגן‪.‬‬ ‫ב‪.‬‬ ‫סרטט סקיצה של גרף הפונקציה‪.‬‬ ‫ג‪.‬‬ ‫(‪ )1‬מצא את האסימפטוטות המקבילות לצירים של פונקציית הנגזרת )‪. f'(x‬‬ ‫(‪ )2‬רשום את התחומים שבהם )‪ f'(x‬שלילית ואת התחומים שבהם היא חיובית‪.‬‬ ‫(‪ )3‬רק על פי תת־סעיפים ג(‪ )1‬ו־ ג(‪ ,)2‬סרטט סקיצה של גרף פונקציית הנגזרת )‪. f'(x‬‬ ‫תשובה לשאלה ‪3‬‬ ‫א‪ )1( .‬המכנה של )‪ f(x‬צריך להיות שונה מ־ ‪ , 0‬לכן‪:‬‬ ‫‬ ‫תחום ההגדרה של )‪: f(x‬‬ ‫‬ ‫‪x + 3! 0‬‬ ‫‪0‬‬ ‫‪x !- 3‬‬ ‫‪5‬‬ ‫‪f (0) = - 3‬‬ ‫‬ ‫ (‪)2‬‬ ‫‪x =! 5‬‬ ‫‬ ‫‬ ‫&‬ ‫‪x2 - 5 = 0‬‬ ‫&‬ ‫‪5‬‬ ‫‪b0 , - 3 l‬‬ ‫‪f (x) = 0‬‬ ‫‪^! 5 , 0h‬‬ ‫‪x =- 3‬‬ ‫ (‪)3‬‬ ‫אסימפטוטה אנכית‪:‬‬ ‫ (‪)4‬‬ ‫הנגזרת של הפונקציה )‪ f(x‬היא‪:‬‬ ‫‪2x (x + 3) - (x2 - 5) x2 + 6x + 5‬‬ ‫=‬ ‫‪(x + 3) 2‬‬ ‫‪(x + 3) 2‬‬ ‫‪x2 + 6x + 5 = 0‬‬ ‫‬ ‫&‬ ‫= )‪f' (x‬‬ ‫‪f' (x) = 0‬‬ ‫‪0‬‬ ‫‬ ‫‬ ‫הסימן של הנגזרת השנייה )‪f''(x‬‬ ‫‬ ‫נקבע על פי הנגזרת של המונה של )‪f'(x‬‬ ‫‬ ‫כאשר המכנה חיובי‪ ,‬לכן הסימן ייקבע על פי‪:‬‬ ‫‬ ‫‬ ‫לפונקציה )‪ f(x‬יש‪:‬‬ ‫‬ ‫&‬ ‫‪/‬המשך בעמוד ‪/4‬‬ ‫נקודות החיתוך עם הצירים‪:‬‬ ‫‬ ‫‬ ‫‬ ‫‪x=0‬‬ ‫‪x =-1 , x =- 5‬‬ ‫‪f'' (x) = 2x + 6‬‬ ‫סימן‬ ‫‪0‬‬ ‫‪f'' (- 5) 1 0 , f'' (- 1) 2 0‬‬ ‫סימן‬ ‫סימן‬ ‫‪0‬‬ ‫מינימום ב־ )‪ , (- 1 , - 2‬מקסימום ב־ )‪(- 5 , - 10‬‬ ‫‪/‬המשך בעמוד ‪/7‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪-7‬‬‫המשך תשובה לשאלה ‪.3‬‬ ‫ב‪.‬‬ ‫‪y‬‬ ‫)‪f(x‬‬ ‫‪x‬‬ ‫‪-2‬‬ ‫‪-5-3 -1‬‬ ‫‪- 10‬‬ ‫‬ ‫ג‪.‬‬ ‫(‪)1‬‬ ‫אסימפטוטות של )‪: f'(x‬‬ ‫‬ ‫(‪)2‬‬ ‫לפי הגרף של )‪ f(x‬נקבל‪:‬‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫‪y =1 , x =- 3‬‬ ‫‪0‬‬ ‫‪-1‬‬ ‫‪3‬‬ ‫‬ ‫‪+‬‬ ‫)‪ f'(x‬שלילית עבור‪:‬‬ ‫)‪ f'(x‬חיובית עבור‪:‬‬ ‫‬ ‫‪0‬‬ ‫(‪)3‬‬ ‫‬ ‫)‪f'(x‬‬ ‫‪x‬‬ ‫‪-2‬‬ ‫‪-3‬‬ ‫‪-4‬‬ ‫‪4‬‬ ‫‪4‬‬ ‫‪-‬‬ ‫‪-‬‬ ‫‪-5‬‬ ‫‪-6‬‬ ‫‪3‬‬ ‫‪0‬‬ ‫‪+‬‬ ‫‪x‬‬ ‫)‪f(x‬‬ ‫)‪f'(x‬‬ ‫‪- 5 1 x 1- 3 , - 3 1 x 1- 1‬‬ ‫‪x 1- 5 , x 2- 1‬‬ ‫‪y‬‬ ‫‪-1‬‬ ‫‪-3‬‬ ‫‪-5‬‬ ‫המשך בעמוד ‪/8‬‬ ‫של פונקציות טריגונומטריות‪ ,‬פונקציות מעריכיות ולוגריתמיות‬ ‫‪2‬‬ ‫ופונקציות חזקה ( ‪ 66 3‬נקודות)‬ ‫‪1‬‬ ‫ענה על שתיים מהשאלות ‪( 5-3‬לכל שאלה — ‪33 3‬‬ ‫נקודות)‪-.‬‬ ‫‪8-‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫שים לב! אם תענה על יותר משתי שאלות‪ ,‬ייבדקו רק שתי התשובות הראשונות שבמחברתך‪.‬‬ ‫שאלה ‪4‬‬ ‫‪.3‬‬ ‫יובל פתח חשבון חדש בבנק והפקיד בו ‪ 10,000‬שקל‪.‬‬ ‫א‪.‬‬ ‫גדל בכל חודש ב־ ‪. 2%‬‬ ‫הסכום שהפקיד ֵ‬ ‫כעבור שנה מרגע ההפקדה משך יובל מחשבונו ‪ 5000‬שקל‪.‬‬ ‫(הסכום שנשאר ממשיך לגדול בכל חודש ב־ ‪).2%‬‬ ‫כעבור כמה חודשים מרגע המשיכה‪ ,‬שוב יהיו בחשבונו של יובל ‪ 10,000‬שקל?‬ ‫‪3‬‬ ‫‪2x‬‬ ‫נתונה הפונקציה ‪f (x) = 2x + 3‬‬ ‫ב‪.‬‬ ‫‪y‬‬ ‫בתחום ‪. x 2 0‬‬ ‫העבירו ישר המשיק לגרף הפונקציה‬ ‫בנקודת הקיצון שלה‪ ,‬והעבירו את‬ ‫‪1‬‬ ‫הישר ‪ y = 2 6‬החותך את גרף הפונקציה‬ ‫בין היתר בנקודה שבה ‪x = 1‬‬ ‫(הנקודה הקרובה לציר ה־ ‪.) y‬‬ ‫‪x‬‬ ‫מצא את השטח המוגבל על ידי שני הישרים‪ ,‬על ידי גרף הפונקציה )‪ f(x‬ועל ידי ציר ה־ ‪, y‬‬ ‫השטח המקווקו בציור‪.‬‬ ‫הערה‪ :‬אין קשר בין סעיף א לסעיף ב‪.‬‬ ‫תשובה לשאלה ‪4‬‬ ‫א‪.‬‬ ‫הסכום בבנק כעבור ‪ 12‬חודשים‪:‬‬ ‫‬ ‫‬ ‫הסכום בבנק לאחר המשיכה‪:‬‬ ‫‬ ‫כעבור ‪ x‬חודשים כדי שיהיו בבנק‬ ‫‬ ‫שוב ‪ 10,000‬שקלים צריך להתקיים‪:‬‬ ‫‬ ‫‬ ‫על ידי הפעלת ‪,n‬‬ ‫‬ ‫על שני אגפי המשוואה נקבל‪:‬‬ ‫‬ ‫‬ ‫‪/‬המשך בעמוד ‪/4‬‬ ‫‪10, 000 #1.0212‬‬ ‫‪0‬‬ ‫‪10, 000 #1.0212 - 5000‬‬ ‫‪^10, 000 #1.0212 - 5000h 1.02 x = 10, 000‬‬ ‫‪0‬‬ ‫‪10, 000‬‬ ‫‪m‬‬ ‫‪10, 000 $1.0212 - 5000‬‬ ‫‪,n1.02‬‬ ‫‪,n c‬‬ ‫=‪x‬‬ ‫‪0‬‬ ‫‪ 13.3‬חודשים = ‪x‬‬ ‫‪/‬המשך בעמוד ‪/9‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪-9‬‬‫המשך תשובה שאלה ‪.4‬‬ ‫ב‪.‬‬ ‫הנגזרת של )‪: f(x‬‬ ‫‬ ‫‬ ‫‪2‬‬ ‫‪3‬‬ ‫‪+‬‬ ‫‪2x2 3‬‬ ‫‪3‬‬ ‫‪3‬‬ ‫) ‪ x = - 2‬לא בתחום ( ‪x = 2‬‬ ‫&‬ ‫‪f' (x) = -‬‬ ‫‪x 2 0 , f' (x) = 0‬‬ ‫‪3‬‬ ‫‪fb 2 l = 2‬‬ ‫שיעור ה־ ‪ y‬של נקודת הקיצון‪:‬‬ ‫‪0‬‬ ‫‬ ‫‬ ‫משוואת הישר המשיק בנקודת הקיצון‪:‬‬ ‫‬ ‫השטח המבוקש מורכב משני שטחים‪:‬‬ ‫‬ ‫שטח מלבן הנוצר מהמשיק‪ ,‬מהישר ‪, y = 2 6‬‬ ‫‪1‬‬ ‫‬ ‫מהאנך ‪ x = 1‬ומציר ה־ ‪: y‬‬ ‫‬ ‫שטח המוגבל על ידי הגרף של )‪, f(x‬‬ ‫‬ ‫על ידי המשיק ועל ידי האנך ‪: x = 1‬‬ ‫‬ ‫‬ ‫‬ ‫‪y=2‬‬ ‫השטח המבוקש הוא‪:‬‬ ‫‪1‬‬ ‫‪1‬‬ ‫‪S I = (2 6 - 2) $1 = 6‬‬ ‫‪6f (x) - 2@ dx‬‬ ‫‪3‬‬ ‫‪2‬‬ ‫‪3‬‬ ‫‪2‬‬ ‫‪#‬‬ ‫‪1‬‬ ‫= ‪S II‬‬ ‫‪0‬‬ ‫‪3‬‬ ‫‪x2‬‬ ‫‪3 3‬‬ ‫‪7‬‬ ‫‪S II = ; 2 ,nx + 3 - 2xE = 2 ,n 2 - 12 = 0.02486‬‬ ‫‪1‬‬ ‫‪3 3‬‬ ‫‪5‬‬ ‫‪S I + S II = 2 ,n 2 - 12 = 0.1915‬‬ ‫‪/‬המשך בעמוד ‪/10‬‬ ‫ג‪.‬‬ ‫בתחום הנתון סרטט סקיצה של גרף הפונקציה )‪. f(x‬‬ ‫ד‪.‬‬ ‫בתחום הנתון מצא את השטח המוגבל על ידי גרף הפונקציה )‪ , f(x‬על ידי המשיק ‪y = 3‬‬ ‫ועל ידי ציר ה־ ‪. y‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫‪- 10 -‬‬ ‫שאלה ‪5‬‬ ‫נתונה הפונקציה ‪ a , f (x) = (a - 3x) e3x‬הוא פרמטר‪.‬‬ ‫‪.5‬‬ ‫א‪.‬‬ ‫מהו תחום ההגדרה של הפונקציה?‬ ‫ב‪.‬‬ ‫ידוע כי שיעור ה־ ‪ x‬של נקודת הקיצון של הפונקציה )‪ f(x‬הוא ‪. 1‬‬ ‫מצא את הערך של ‪. a‬‬ ‫הצב ‪ , a = 4‬וענה על הסעיפים ג ו־ ד‪.‬‬ ‫(‪ )1‬מצא את תחומי העלייה והירידה של הפונקציה )‪. f(x‬‬ ‫ג‪.‬‬ ‫(‪ )2‬מצא את נקודות החיתוך של גרף הפונקציה )‪ f(x‬עם הצירים‪.‬‬ ‫(‪ )3‬סרטט סקיצה של גרף הפונקציה )‪. f(x‬‬ ‫נתון הישר ‪. k # 0 , y = k‬‬ ‫ד‪.‬‬ ‫כמה נקודות חיתוך יש לישר זה עם גרף הפונקציה )‪ ? f(x‬נמק‪.‬‬ ‫א‪.‬‬ ‫הפונקציה מוגדרת לכל ‪x‬‬ ‫תשובה לשאלה ‪5‬‬ ‫בהצלחה!‬ ‫ב‪.‬‬ ‫נגזרת הפונקציה )‪: f(x‬‬ ‫‪f' (x) = - 3e3x + (a - 3x) e3x $ 3‬‬ ‫זכות היוצרים שמורה למדינת ישראל‬ ‫אין להעתיק או לפרסם אלא ברשות משרד החינוך‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫יש קיצון ב־ ‪ , x = 1‬לכן‪:‬‬ ‫‬ ‫‬ ‫‬ ‫‬ ‫‪0‬‬ ‫)‪f' (x) = 3e3x (a - 3x - 1‬‬ ‫‪0‬‬ ‫)‪f' (1) = 3e3 (a - 3 - 1‬‬ ‫‪f' (1) = 0‬‬ ‫‪0‬‬ ‫‪a - 3 - 1 = 0 , 3e3 2 0‬‬ ‫‪0‬‬ ‫‪a=4‬‬ ‫‪/‬המשך בעמוד ‪/11‬‬ ‫מתמטיקה‪ ,‬חורף תשע"ד‪ ,‬מס' ‪035004‬‬ ‫ ‪- 11‬‬‫המשך תשובה לשאלה ‪.5‬‬ ‫ג‪.‬‬ ‫(‪)1‬‬ ‫)‪f' (x) = 3e3x (3 - 3x‬‬ ‫קיבלנו‪:‬‬ ‫‬ ‫‪0‬‬ ‫‪x 21‬‬ ‫‪1‬‬ ‫‪x 11‬‬ ‫‪x‬‬ ‫‪-‬‬ ‫‪0‬‬ ‫‪+‬‬ ‫)‪f'(x‬‬ ‫‪3‬‬ ‫)‪f(x‬‬ ‫‪4‬‬ ‫‬ ‫הפונקציה )‪ f(x‬עולה עבור‪:‬‬ ‫‪x 11‬‬ ‫‬ ‫הפונקציה )‪ f(x‬יורדת עבור‪:‬‬ ‫‪x 21‬‬ ‫(‪)2‬‬ ‫‬ ‫‪f (x) = (4 - 3x) e3x‬‬ ‫קיבלנו‪:‬‬ ‫‬ ‫‪f (0) = 4‬‬ ‫&‬ ‫‪x=0‬‬ ‫‬ ‫‪4‬‬ ‫‪x= 3‬‬ ‫&‬ ‫‪f (x) = 0‬‬ ‫‬ ‫חיתוך עם ציר ה־ ‪: x‬‬ ‫‬ ‫חיתוך עם ציר ה־ ‪: y‬‬ ‫‪4‬‬ ‫‪b 3 , 0l‬‬ ‫‪^ 0 , 4h‬‬ ‫‬ ‫(‪)3‬‬ ‫‪y‬‬ ‫)‪f(x‬‬ ‫‪4‬‬ ‫‪x‬‬ ‫ד‪.‬‬ ‫‪4‬‬ ‫‪3‬‬ ‫‬ ‫‪1‬‬ ‫‪y‬‬ ‫)‪f(x‬‬ ‫‪x‬‬ ‫‪y=k‬‬ ‫‬ ‫לפי הסרטוט‪ :‬הישר חותך את הגרף של )‪ f(x‬בנקודה אחת עבור ‪k # 0‬‬ ‫זכות היוצרים שמורה למדינת ישראל‬ ‫אין להעתיק או לפרסם אלא ברשות משרד החינוך‬