. נחשב את השדה המגנטי בעזרת חוק ביו סבר 4 . לשני המוליכים הישרים שמחברים
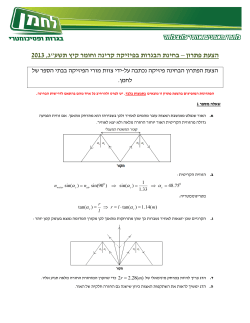
ʹ1ʤʬʠ .4נחשב את השדה המגנטי בעזרת חוק ביו סבר. μ0 I dL × r = dB ⋅ 4π r3 לשני המוליכים הישרים שמחברים את הקשתות האבר בחוק ביו סבר של dL || r → dL × r = 0 dL × rמקיים כאשר P r הוא המרחק לנקודה .P dL P r לכן התרומה היחידה תהיה משתי הקשתות ברדיוסים . R1 , R2נקבע כיוון חיובי לתוך הדף ,ונחשב שדה מגנטי של טבעת ברדיוס Rבזוית פתיחה של θע"י חלוקת הקשת למקטעים קטנים שהשדה שכל מקטע קטן יוצר נתון לפי חוק ביו-סוור. dL R θ מכוון שהקשת ברדיוס קבוע P r =R ואלמנט הזרם שאורכו dL ניצב לרדיוס ) μ I dL ⋅ R ⋅ sin (90 ⋅ dB = 0 4π R3 )גיאומטריה( לכן: לפי הביטוי של אורך קשת: μ0 I R ⋅ dθ ⋅ 4π R2 = dB סכומים על כל תחום הזוויות ומקבלים את B μ 0 I θ dθ μ 0 I θ = ⋅ 4π ∫0 R 4π R לכן למערכת שבבעיה השדה המגנטי הוא: הסיבה שמחסירים את B2 − B1 ⎞ μ0 I ⎛ 1 1 ⎟ θ⎜ − ⎠⎟ 4π ⎜⎝ R2 R1 =B = B = B2 − B1 היא כי כיווני הזרמים הפוכים בשתי הקשתות. ⎞ μ0 I ⎛ R1 − R2 ⎟ ⎜θ ⎠⎟ 4π ⎜⎝ R1 ⋅ R2 =B נציב מספרים: ⎞ 4π ⋅ 10−73.6 2π ⎛ 0.45 − 0.17 ⎜ ⎟ = 2.75μT = 0.0275G 4π ⎠ 3 ⎝ 0.45 ⋅ 0.17 =B שאלה 2 כדי לחשב את השדה נחשב את התרומה של כל אחד מקטעי התיל ,שני הקטעים הישרים והקשת המעגלית. עבור הקטעים הישרים: ƌ Z ɽ dž R R √= 2 r R + x2 = sin θ d` = dx, ˆ ∞ ˆ R Id` sin θ µ0 ∞ Idx · √R2 +x2 µ0 IR x √ = = 2 2 2 r 4π 0 R +x 4π R2 x2 + R2 0 µ0 I µ0 I 1 q = −0 2 4πR 4πR ∞→x 1+ R x2 µ0 4π = = השדות של שני התיילים בכיוון יוצא מהדף לפי חוק ביו־סבר ,לכן התרומה שלהם µ0 I 4πR · B1 = 2 עבור הקשת המעגלית: α = 90o IRd` sin 90o µ0 Iθ = R2 4πR θ ˆ 0 d` = Rdθ, Id` sin α µ0 = r2 4π ˆ µ0 = 4π השדה שהיא יוצרת בכיוון יוצא מהדף ,לכן µ0 I θ 4πR B2 = − אנחנו דורשים שהשדה הכולל יתאפס ,לכן µ0 I (2 − θ) = 0 4πR = Btot = B1 + B2 מכאן ]θ = 2 [rad 1 Bcirc Bstaright
© Copyright 2026