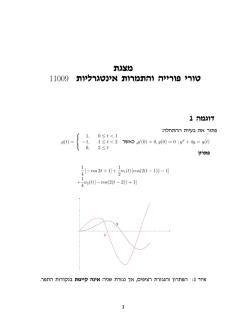
פתרון - studenteen
אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 1 ] C 1 [a, bהוא מרחב הפונקציות הגזירות ברציפות בקטע ]. [a, b לכל ] f , g ∈ C 1 [a, bנגדיר פעולה הבאה: b ( f , g ) = ∫ f ′(x )g ′(x )dx a האם פעולה זו מהווה מכפלה פנימית? פתרון: נתבונן למשל ב : f ≡ 1 f ∈ C 1 [a, b] .1 f ≠ 0 .2 ובכל זאת b b a a ( f , f ) = ∫ f ′(x ) f ′(x )dx = ∫ 0dx = 0 לכן זו איננה מכפלה פנימית. אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 2 נתונה פונקציה f ( x ) = sin x ⋅ sin 2 xבקטע ] , [− π , πכאשר ∞ a0 ] + ∑ [a n cos nx + bn sin nx 2 n =1 הינו הטור פוריה שלה בקטע זה. ∞ הוכח/י כי . ∑ (− 1) nbn = 0 n n =1 פתרון: נציין את תכונות הפונקציה f ( x) = sin x ⋅ sin 2 xבקטע ] : [− π , π f (x) .1היא פונקציה רציפה ואי זוגית בקטע ] . [− π , π . f (−π ) = f (π ) = 0 .2 .3הנגזרת ) f ′(xהיא פונקציה רציפה למקוטעין וזוגית f ′(0) = f ′(π ) = f ′(−π ) = 0 .4בנקודה π 2 x = ±לנגזרת ) f ′(xיש קפיצה כי ⎞ ⎛ ⎛ π ⎞+ ⎞ ⎛ ⎛ π ⎞− f ′⎜ ⎜ ⎟ ⎟ = − f ′⎜ ⎜ ⎟ ⎟ ≠ 0 ⎟ ⎠ ⎜⎝ 2 ⎟ ⎠ ⎜⎝ 2 ⎝ ⎠ ⎝ ⎠ + ⎞ ⎞ ⎛⎛ π ⎞ ⎛ ⎛ π ⎞− ⎜ ⎟ f ′ ⎜ − ⎟ = − f ′⎜ − ⎜ ⎟ ⎟ ≠ 0 ⎟ ⎠ ⎜⎝ 2 ⎟ ⎠⎜ ⎝2 ⎝ ⎠ ⎝ ⎠ בגלל ש f (x) -היא פונקציה אי-זוגית ,טור פורייה שלה בקטע ] [− π , πהוא מהצורה ∞ , f ( x) ~ ∑ bn sin nx n =1 כל התנאים של משפט הגזירה מתקיימים ,ולכן הטור פורייה של הנגזרת ) f ′(xהוא ∞ f ′( x) ~ ∑ nbn cos nx n =1 על פי התכונות של ) f (xו f ′(x) -נוכל להציב x = πונקבל כי: nbn = f ′(π ) = 0 ∞ n )∑ (−1 n =1 אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 3 מצא/י את טור פורייה של f (x ) = xבקטע ] . [− π , π ∞ 1 מהו סכום הטור ? ∑ 4 n =1 n פתרון: 2 π 2 ∞ 4(− 1)n ∑+ cos nx 3 n =1 n 2 ~ x2 על פי שוויון פרסבל נקבל כי 1 π4 = ∑ 4 90 n =1 n ∞ )הערה :פתרון מלא נמצא בספרו של סמי זעפרני ואלן פנקס "טורי פורייה והתמרות אינטגרליות" ,עמ' (.67 ,43 אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 4 נתונה בעיית שטורם ליוביל הבא: ⎧ y ′′ + λy = 0, 0 < x < π ⎪ ⎨ y ′(0) = 0 ⎪ y (π ) = 0 ⎩ מצא/י את הערכים העצמיים )הממשיים( ואת הפונקציות העצמיות המתאימות לכל ערך עצמי. פתרון: נחלק למקרים: מקרה א'. λ = 0 : y′′ = 0 ⇒ y′ = c1 ⇒ y = c1 x + c2 נציב תנאי שפה ונקבל כי , c1 = c2 = 0כלומר אין פתרון לא טריביאלי לבעיה. מקרה ב') . λ > 0 :הערה :עבור λ < 0תנאי שפה לא מתקיימים(. במקרה זה נקבל משוואה אופיינית הבאה: k 2 + λ = 0 ⇒ k 2 = −λ ⇒ k1, 2 = ±i λ ופתרון הכללי יהיה מהצורה הבאה: y (x ) = C1 cos λ x + C2 sin λ x ⇒ y′( x ) = − λ C1 sin λ x + λ C2 cos λ x כעת נציב את תנאי השפה: y′(0) = − λ C1 sin 0 + λ C2 cos 0 = 0 ⇒ C2 = 0 C1 ≠ 0 ⇒ cos λ π = 0 (2n + 1)π 2 y (π ) = 0 ⇒ y (π ) = C1 cos λ π = 0 2 = ⇒ λπ ⎞ )⎛ (2n + 1 ⎜= ⇒λ ⎟ ⎠ ⎝ 2 ⎞ ⎛ 2n + 1 ⎜ = , λnוהפונקציות העצמיות לסיכום קיבלנו כי סדרת הערכים העצמיים היא ⎟ ⎠ ⎝ 2 2n + 1 . n = 0,1,2,... , ϕ n = cos המתאימות לכל ערך עצמי הןx : 2 2 אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 5 נתונה פונקציה ) f ∈ G (Rכך שהתמרת פורייה שלה היא 1 3 1+ ω = ) . F [ f ](ω ∞ חשב/י את האינטגרל הבאdx : 2 ) ∫ ( f ∗ f ′)(x .נמק/י את תשובתך. ∞− פתרון: 1 3 1+ ω iω 3 1+ ω F →⎯⎯ )f ( x = ) F (ω F →⎯⎯ )f ′( x = ) iω ⋅ F (ω על פי משפט קונבולוציה נקבל כי: 2πiω ) (1 + ω 3 2 = iω 3 1+ ω ⋅ 1 3 1+ ω F →⎯⎯ )( f ∗ f ′)( x ⋅ 2π כעת נשתמש במשפט פלנשראל ונקבל כי: dω 3ω 2 ∞ ) ∫ (1 + ω 3 4 0 8π 2 3 = dω 4π 2ω 2 ) (1 + ω 3 4 ∞ ∫ dω = 2 0 2 4π 2 ω ) (1 + ω 3 4 ∞ ∫ 2 = dω ∞ ) 2 ∞− ( נבצע הצבה , 1 + ω 3 = t :ונקבל כי , 3ω 2 dω = dtולכן ∞ ∞ ∞ ⎤ 16π 3 dt 16π 3 ⎡ t −3 16π 3 ′ ( () ) ∗ = ⋅ = ⋅ = f f x dx ⎢ ⎥ ∫ 3 ∫0 t 4 3 ⎣ − 3⎦0 9 ∞− 2 ∞ 1 2πiω 2 ∫ = ⋅ ∫ ( f ∗ f ′)( x ) dx 3 ∞2π − −∞ 1 + ω אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 6 מצא/י פתרון למשוואה הבאה: ⎧ ⎪⎪ f ′′(t ) + 2 f (t ) = 3∫ (t − z ) f ( z )dz, 0 ⎨ ⎪ f (0) = 0, f ′(0) = 1 ⎩⎪ t t≥0 פתרון: נשים לב כי מדובר במשוואה . f ′′(t ) + 2 f (t ) = 3t ∗ f (t ) :התמרת לפלס של המשוואה מתקבלת באופן הבא: 1 s2 ⋅ F ( s ) ⇒ F ( s ) = s2 )( s 2 − 1)( s 2 + 3 ⋅ s 2 F ( s ) − sf (0) − f ' (0) + 2 F ( s ) = 3 כעת נפרק את התוצאה לשברים חלקיים: s2 1 1 1 1 3 1 = − + 2 2 ( s − 1)( s + 3) 8 s − 1 8 s + 1 4 s 2 + 3 = )F (s נחשב התמרה הפוכה ונקבל: ) ( 1 1 3 1 ⎞ 1 t 1 −t 3 ⎛1 1 − + ⎜ f (t ) = F −1 sin 3t ⎟= e − e + 2 8 4 ⎝ 8 s −1 8 s +1 4 s + 3 ⎠ 8 אוניברסיטת בר אילן ,הפקולטה למתמטיקה. קורס ,88-235-02 :אנליזת פורייה והתמרות אינטגרליות. מרצה :מיכאל מיכאלי. פתרון מועד א' ,סמסטר קיץ ,תשס"ח. שאלה 7 ⎧1 x < 1 נתונה פונקציה ⎨ = ) . g (x ⎩0 x ≥ 1 א .חשב/י את ) . g ( x ) ∗ g ( x פתרון: x <2 x ≥2 ⎧2 − x ⎩ 0 ⎨ = ) (g ∗ g )(x ב .חשב/י את התמרת פורייה ) . F [g (x ) ∗ g (x )](ω פתרון: נחשב את התמרת פורייה בעזרת משפט הקונבולוציה: sin ω sin ω 2 sin 2 ω F [g ( x ) ∗ g ( x )](ω ) = 2πF [g ( x )](ω ) ⋅ F [g ( x )](ω ) = 2π ⋅ = 2 πω πω πω ∞ sin 4 x ג .חשב/י את . ∫ 4 dx x ∞− פתרון: נשתמש במשפט פלנשראל: 2 ⎤ π ⎡ (2 − x )3 2π = ⎥ 3 ⎦0 3 2 ⎣⎢ ⋅ ∫ (2 − x ) dx = 4 2 −2 2 ∞ ⎞ ⎛ 2 sin 2 ω π2 1 ⎟ ⎜ = ⋅ ω d ⎠⎟ ∫ ⎜ πω 2 4 2π ⎝∞− ∞ π2 sin 4 x = dx ∫ x4 4 ∞−
© Copyright 2026