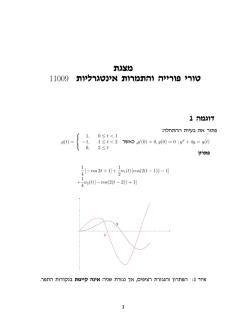
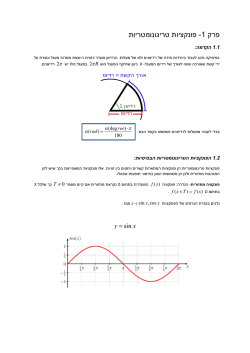
20152-2 חשבון אינפי `7. דף תרגילים מס באילוץ ומוחלט אקסטרמום פתרונות
חשבון אינפי 20152-2 דף תרגילים מס' .7 אקסטרמום באילוץ ומוחלט פתרונות ותשובות .1מצא את מקסימום ומינימום מוחלטים )הערך המקסימאלי והערך המינימאלי( של ) f ( x, yבתחום הסגור .D 2 3 2 2 )א( D , f ( x, y ) 4 x 2 x y yמוגבל על ידי הגרפים y xו. y 9 - מכיוון שהפונקציה רציפה ב Dכולו וגם Dהוא תחום סגור ,לכן לפי משפט ווארשטרס יש מינימום ומקסימום מוחלטים. 2 2 3 f x 12 x 4 xy 0 12 x 4 x 0 x 0 x 3 , 2 y x2 f y 2 x 2 y 0 y 0 y 9 נציב את הנקודות האלה בפונקציהf (0,0) 0, f 3,9 27 : נחשב עכשיו לפי שפות: 3 2 f x, y 4 x 18 x 81 L1 : y 9,3 x 3 f 12 x 2 36 x 12 x x 3 x 0, x 3 f 3,9 27 f 0,9 81, f 3,9 189, עכשיו לפי השפה שניה L2 : y x 2 ,3 x 3 f x, y 4 x 3 2 x 4 x 4 4 x 3 x 4 f 12 x 2 4 x 3 4 x 2 3 x 0 x 0, x 3 לכן המסקנהf max f 0,9 81 : f 0,0 0 f min f (3,9) 189 f 3,9 27 f 3,9 189, )ב( D , f ( x, y ) x 2 y 2הוא משולש שצלעותיו . y 0 , x 0 ,2 x y 2 פתרון: נמצא נקודות קיצון בתוך התחום f 2 x 0 x x 0 f y 2y 0 y 0 נציב את הנקודה בפונקציהf (0,0) 0 : נחשב לפי השפות: f x, y x 2 L1 : y 0, 0 x 1 f 1,0 1 f 0,0 0, f x, y y 2 L2 : x 0, 0 y 2 f 0,0 0, f 0,2 4 L3 : y 2 2 x, 0 x 1 f 1,0 1, f 0,2 4 f x, y 5 x 2 8 x 4 f (0.8,0.4) 0.8 :יש לקחת בחשבון את קודקוד של פרבולה f min f (0,0) 0 f max f 0,2 4 :לכן המסקנה D ( x, y ) 0 x 9 , 0 y 5 , f ( x, y ) y x y 2 x 6 y ()ראה שרטוט ()ג (0 y 5) , (0 x 9) : D נמצא את הנקודות הקריטיות בתוך תחום y f x 2 x 1 0 f x 2y 6 0 y y 2 x 0 2 y x 6 f (9,0) 9 , f (0,0) 0 , f ( x,0) x f (0, y ) y 2 6 y f y 2 y 6 0 y 3 f (0,3) 9 , f (0,5) 5 f (9, y ) 3 y y 2 9 6 y y 2 9 y 9 9 f y 2 y 9 0 y 2 9 f (9, ) 11.25 , f (9,5) 11 2 x 4 y 4 f (4,4) 12 נמצא את נקודות קריטיות על השפה :( נקבל0 x 9) y 0 , x -( לאורך ציר ה1 :( נקבל0 y 5) x 0 , y -( לאורך ציר ה2 :( נקבל0 y 5) x 9 ( לאורך הישר3 :( נקבל0 x 9) y 5 ( לאורך הישר4 f ( x,5) 5 x 25 x 30 x 5 x 5 5 f x 1 0 5 2 x 0 x 6.25 2 x f (6.25,5) 11.25 :נרכז את כל הנקודות הקריטיות וערכי הפונקציה באותן הנקודות בטבלה הנקודות (4,4) (0,0) f ( x, y ) 12 0 (9,0) (0,3) (0,5) 9 5 9- f min f (9,0) 9 , f max f (4,4) 12 D ( x, y ) x 2 y 2 1 9 (9, ) 2 11.25 (9,5) (6.25,5) 11 11.25 , f ( x , y ) 2 x 3 y 4 () ד x 2 y 2 1 : D נמצא את הנקודות הקריטיות בתוך תחום ()ראה שרטוט f x 6 x 2 0 3 f y 4 y 0 x 0 y 0 f (0,0) 0 : בהצגה פרמטריתx y 1 נרשום את משוואת המעגל.נמצא את נקודות קריטיות על השפה 2 2 x cos t , 0 t 2 y sin t f ( x(t ), y (t )) 2 cos 3 t sin 4 t f t 2 3 cos 2 t ( sin t ) 4 sin 3 t cos t 2 cos t sin t (2 sin 2 t 3 cos t ) 0 sin 2t 0 או2 sin 2 t 3 cos t 0 3 t0 , t , t , t , t 2 : הוא0 t 2 כאשרsin 2t 0 פתרון למשוואה 2 2 f ( x(0), y (0)) f (1,0) 2 f ( x( ), y ( )) f (0,1) 1 2 2 f ( x( ), y ( )) f (1,0) 2 3 3 f ( x( ), y ( )) f (0,1) 1 2 2 f ( x(2 ), y (2 )) f (1,0) 2 2 sin 2 t 3 cos t 0 :נפתור את המשוואה 2 2(1 cos t ) 3 cos t 0 2 cos 2 t 3 cos t 2 0 3 9 422 3 5 1 4 4 2 פתרון למשוואה הוא: cos t 5 , t 3 3 t 1 3 13 f ( x( ), y ( )) f ( , ) 3 3 2 2 16 5 5 1 3 13 f ( x( ), y ( )) f ( , ) 3 3 2 2 16 נרכז את כל הנקודות הקריטיות וערכי הפונקציה באותן הנקודות בטבלה: 1 3 ) ( , 2 2 13 16 1 3 ) ( , 2 2 13 16 )(0,1 1 )(1,0 )(0,1 )(1,0 )(0,0 הנקודות -2 1 2 0 ) f ( x, y f min f (1,0) 2 , f max f (1,0) 2 )ה( D , f ( x, y ) xye 4 x 3 yהוא הרביע הראשון של המישור . xy נמצא את הנקודות הקריטיות בתוך תחום y 0 , x 0 : D x 0 y 0 x 1 4 1 y 3 y (1 4 x) 0 x(1 3 y ) 0 f x e 4 x 3 y ( y 4 xy ) 0 4 x 3 y ( x 3xy ) 0 f y e 1 1 1 , f (0,0) 0 f( , ) 4 3 12e 2 נמצא את נקודות קריטיות על השפה (1לאורך ציר ה (0 x ) y 0 , x -נקבלf ( x,0) 0 : (2לאורך ציר ה (0 y ) x 0 , y -נקבלf (0, y ) 0 : 1 1 1 בין הערכים של ) f ( x, yבנקודות קריטיות מקבלים: f min f (0,0) 0 , f max f ( , ) 4 3 12e 2 .2מצא את המקסימום המוחלט ואת המינימום המוחלט של הפונקציה 2 2 f ( x, y ) ( x 2 2 y 2 ) e x y בעיגול היחידה . x 2 y 2 1 נמצא נקודות קיצון בתחום 2 2 x y 2 2 f x e 2 x(1 x 2 y ) 0 x 0 x 2 y 2 2 y (2 x 2 y 2 ) 0 f y e y 0 נציב את הנקודה בפונקציהf (0,0) 0 : f x, y e ( x 2(1 x )) e 1 L1 : y 1 x , 1 x 1 2 2 2 1 2 x :נחשב לפי שפות 2 f 2e x 0 x 0 y 1 1 f 1,0 e 11, f 1,0 e 1 , f 0,1 2e 1 f x, y e 1 (2 x 2 ) L2 : y 1 x 2 , 1 x 1 f 2e 1 x 0 x 0 y 1 f 1,0 e 11, f 1,0 e 1 , f 0,1 2e 1 f min f (0,0) 0 f max f 0,1 f 0,1 2e 1 :לכן המסקנה ( x, y ) 0 עם האילוץz f ( x, y ) )אקסטרמום בתנאי( מצא את האקסטרמום של הפונקציה.3 x y 1 , z x 2 y 2 ()א :פתרון y 1 x : )שיטת ההצבה( ממשוואת האילוץ מקבלים:1 דרך : בפונקציהy (x) נציב את z ( x,1 x) x 2 (1 x) 2 z ( x) 2 x 2 2 x 1 : z (x) נמצא את הנקודה הקריטית של z x 4 x 2 0 x 1 2 1 1 z xx ( ) 4 0 - הפונקציה מקבלת את הערך המינימאלי בתנאי מפני שx בנקודה 2 2 2 2 L( x, y, ) x y ( y x 1) :' )שיטת כופלי לגרנז'( נבנה את פונקצית לגרנז:2 דרך : נמצא את הנקודה הקריטית מהמערכת x 2 Lx 2 x 0 L y 2 0 y y 2 L y x 1 0 x y 1 0 2 2 L( x, y,1) x y y x 1 1 x 2 1 y 2 1 :' בפונקצית לגרנז 1 נציב 1 1 L yy ( L xy ) 2 נחשב : ( , ) בנקודה L xx 2 2 1 1 1 1 1 1 ( , ) 0 ( , ) 2 2 0 4 0 . בתנאיz (x) ( נקודת מינימום של, ) , Lxx 2 2 2 2 2 2 2 2 9 x y 4 , f ( x, y ) xy ()ב 2 :'נבנה את פונקצית לגרנז L( x, y, ) xy (9 x y 2 4) :נמצא את הנקודה הקריטית מהמערכת 0 , L yy 2 , Lxx 2 L xy y (1 362 ) 0 x 2y 9 x 2 y 2 4 0 y 18x 0 x 2y 9 x 2 y 2 4 0 Lx y 18x 0 L y x 2y 0 2 2 L 9 x y 4 0 1 1 או y 3xאו , y 3x 6 6 נציב y 3xבמשוואה , 9 x 2 y 2 4 0 2 2 2 2 , 2 ) , ( , 2 ) , ( ( , 2 ) , נקבל נקודות קריטיות ) , 2 3 3 3 3 ערכי הפונקציה באותן הנקודות: 2 2 2 f ( ( ,- 2 ) f , 2) 3 3 3 2 2 2 ( ,- 2 ) f, 2) ( f 3 3 3 .4מצא שלושה מספרים חיובים שסכומם 100ומכפלתם מקסימלית. ( פתרון: f max f min f x, y, z xyz f g g x y z 100 g x, y, z k אם נפתור את המערכת: f x yz 1 f y xz 1 f z xy 1 x y z 100 אם נכפיל משוואה ראשונה ב , x -משוואה שניה ב y -ומשוואה שלישית ב , zאזי נקבל xyz x xyz y מזה נובע xyz z x y z 100 100 x y z x x x 100 x y z 3 לכן המספרים האלה נותנים מכפלה מקסימלית. ) .5אקסטרמום בתנאי( מצא את האקסטרמום של הפונקציה ) u f ( x, y, zלפי תנאי האילוץ: )א( , u x 2 y 2 zכאשר x2 y2 z 2 1 נבנה את פונקצית לגרנז': נמצא את הנקודה הקריטית מהמערכת: )L( x, y, z , ) x 2 y 2 z ( x 2 y 2 z 2 1 L x L y L z L 1 x 2 1 2x 0 y 1 2 2y 0 3 3 או 2 2z 0 2 2 1 z 2 2 2 x y z 1 0 2 x y 2 z 2 1 0 1 2 2 1 2 2 ( , , ) נקבל נקודות קריטיות ( , , ) , 3 3 3 3 3 3 : נחקור את הדיפרנציאל השני בנקודות הקריטיות 2L 2L 2L 2L 2L 2L d 2 L 2 dx 2 2 dy 2 2 dz 2 2 dxdy 2 dxdz 2 dydz xy xz yz z x y 1 2 2 d 2 L 3dx 2 3dy 2 3dz 2 0 : ( נקבל , , ) לאחר חישוב הנגזרות החלקיות בנקודה 3 3 3 1 2 2 : יש מינימום מקומי בתנאיu x 2 y 2 z ( לפונקציה , , ) לכן בנקודה 3 3 3 1 2 2 u min u (- , , ) 3 3 3 3 1 2 2 d 2 L 3dx 2 3dy 2 3dz 2 0 : ( נקבל, , ) לאחר חישוב הנגזרות החלקיות בנקודה 3 3 3 1 2 2 : יש מקסימום מקומי בתנאיu x 2 y 2 z ( לפונקציה, , ) לכן בנקודה 3 3 3 1 2 2 u max u ( ,- , ) 3 3 3 3 y x () ב כאשר, f ( x, y, z ) xy z 2 2 2 2 x y z 4 :1 דרך :'נבנה את פונקצית לגרנז L( x, y, z , 1 , 2 ) xy z 2 1 ( x y ) 2 ( x 2 y 2 z 2 4) :נמצא את הנקודה הקריטית של המערכת L x y 1 2 2 x 0 L y x 1 2 2 y 0 L z 2 z 2 2 z 0 L x y 0 1 L x 2 y 2 z 2 4 0 2 y 1 2 2 x 0 x 1 2 2 y 0 z (1 2 ) 0 x y x 2 y 2 z 2 4 0 1 0 , 2 1 2 או 1 0 , 2 1 y 2 , z0 הנקודות הקריטיות של ) f ( x, y, zלפי תנאי האילוץ הן: )(0,0,2) , (0,0,2 כאשר x 2 , 1 0 , 2 1 1 ) ( 2 , 2 ,0) , ( 2 , 2 ,0כאשר 2 נחקור את הדיפרנציאל השני d 2 Lבנקודות הקריטיות , לאחר חישוב הנגזרות החלקיות בנקודות קריטיות ) (0,0,2) , (0,0,2מקבלים : 2 d L 2dx 2 2dy 2 2dz 2 2dxdy מהאילוצים מקבלים : 1 0 , 2 dx dy 4dz 0 dx dy 2 xdx 2 ydy 2 zdz 0 לכן d 2 L 2dx 2 0 , f max f (0,0,2) f (0,0,2) 4 לאחר חישוב הנגזרות החלקיות בנקודות קריטיות ) ( 2 , 2 ,0) , ( 2 , 2 ,0מקבלים : d L dx 2 dy 2 dz 2 2dxdy 2 מתנאי האילוץ מקבלים : dx dy 0 dx dy 2 2dx 2 2dy 0 לכן d 2 L dz 2 0 , f min f ( 2 , 2 ,0) f ( 2 , 2 ,0) 2 דרך :2 נציב את האילוץ y xבאילוץ x y z 4וגם נציב אותו בפונקציה: ואז נקבל 2 2 אם נסמן g x, z 2 x z 4 2 2 2 f x 2 x g x 4 x f g 2 f z 2 z g z 2 z 2 2 x z 4 2x 2 z 2 4 אם נכפיל משוואה ראשונה ב zוהמשוואה שניה ב xונשווה ביניהן נקבל: f x, z x 2 z 2 2 2 x z 2 4 2 xz 4 xz 2 xz 2 xz 2 x 2 z 2 4 ולכן 2 xz 2 xz 4 xz 2 xz 2 xz 0 חייב ש 0אחרת אין פתרון למערכת .ולכן מקבלים 4נקודות: x 0 y 0, z 2 x0 y0 , z 2 x 2 y 2 , z0 x 2 y 2 z0 f max f 0,0,2 f 0,0,2 4 . f min f 2 , 2 ,0 f 2 , 2 ,0 2 אזי
© Copyright 2026